Teoria dos Grafos Exemplo DFS Exemplo DFS Exemplo DFS

Teoria dos Grafos
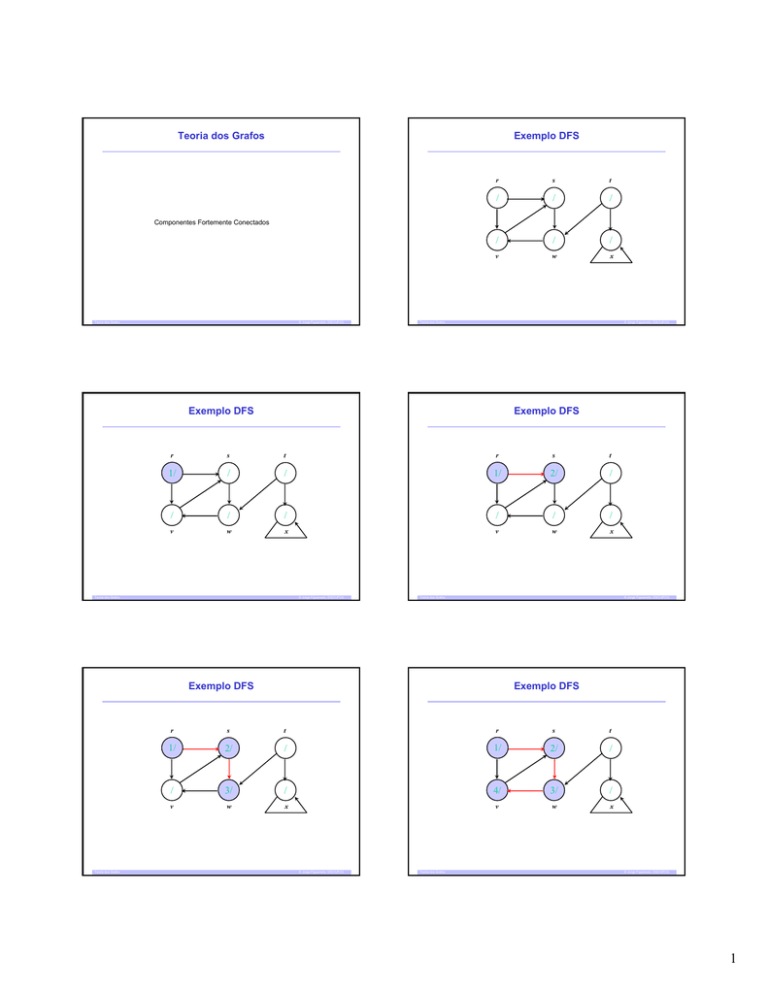
Exemplo DFS
r
s
t
/
/
/
/
/
/
v
w
x
Componentes Fortemente Conectados
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Exemplo DFS
r
t
r
s
t
/
/
1/
2/
/
/
/
/
/
/
/
v
w
x
v
w
x
1/
s
Exemplo DFS
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Exemplo DFS
Teoria dos Grafos
Exemplo DFS
r
s
t
r
s
t
1/
2/
/
1/
2/
/
/
3/
/
4/
3/
/
v
w
x
v
w
x
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
1
Exemplo DFS
Exemplo DFS
r
s
t
r
s
t
1/
2/
/
1/
2/
/
4/5
3/
/
4/5
3/6
/
v
w
x
v
w
x
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Exemplo DFS
r
t
r
s
t
2/7
/
1/8
2/7
/
4/5
3/6
/
4/5
3/6
/
v
w
x
v
w
x
1/
s
Exemplo DFS
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Exemplo DFS
Teoria dos Grafos
Exemplo DFS
r
s
t
r
s
t
1/8
2/7
9/
1/8
2/7
9/
4/5
3/6
/
4/5
3/6
10/
v
w
x
v
w
x
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
2
Exemplo DFS
Teoria dos Grafos
Exemplo DFS
r
s
t
r
s
t
1/8
2/7
9/
1/8
2/7
9/12
4/5
3/6
10/11
4/5
3/6
10/11
v
w
x
v
w
x
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Busca em Profundidade (Revisão)
DFS (Tipos de Arcos)
•• AA busca
busca em
em profundidade
profundidade produz
produz uma
uma floresta
floresta de
de
árvores.
árvores.
•• ÉÉ possível
possível identificar
identificar 44 tipos
tipos de
de arcos:
arcos:
–– Arcos
Arcos da
da árvore:
árvore: arcos
arcos na
na árvore
árvore de
de profundidade.
profundidade.
–– Arcos
Arcos de
de retorno:
retorno: aqueles
aqueles que
que conectam
conectam um
um vértice
vértice
uu aa um
um vértice
vértice ancestral
ancestral na
na árvore
árvore de
de profundidade.
profundidade.
–– Arcos
Arcos forward:
forward: aqueles
aqueles que
que conectam
conectam um
um vértice
vértice uu
aa um
um vértice
vértice descente
descente na
na árvore
árvore de
de profundidade.
profundidade.
–– Arcos
Arcos de
de cruzamento:
cruzamento: os
os demais
demais arcos.
arcos.
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
2/7
t
9/12
C
B
4/5
3/6
v
w
10/11
x
B
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Exemplo SCC
•• Um
Um Grafo
Grafo G
G éé fortemente
fortemente conectado
conectado se,
se, ∀u,v
∀u,v ∈∈ V,
V,
existe
existe um
um caminho
caminho entre
entre uu ee vv ee um
um caminho
caminho entre
entre vv ee
u.
u.
•• Um
Um componente
componente fortemente
fortemente conectado
conectado de
de um
um grafo
grafo éé
um
um subconjunto
subconjunto maximal
maximal de
de vértices
vértices (juntamente
(juntamente com
com
os
os seus
seus correspondentes
correspondentes arcos)
arcos) que
que éé fortemente
fortemente
conectado.
conectado.
Teoria dos Grafos
s
F
Componente Fortemente Conectado (SCC)
Fortemente
Conectado
r
1/8
r
s
t
u
v
w
x
y
Não é Fortemente
Conectado
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
3
Exemplo SCC
Grafo de Componentes
r
s
t
u
v
w
x
y
Teoria dos Grafos
SCC =
SCC,, E
SCC).
•• G
GSCC
= (V
(VSCC
ESCC
).
SCC
•• VVSCC tem
tem um
um vértice
vértice para
para cada
cada SCC
SCC em
em G.
G.
SCC tem
•• EESCC
tem um
um arco
arco se
se existe
existe um
um arco
arco entre
entre os
os
correspondentes
correspondentes SCCs
SCCs em
em G.
G.
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Transposto de um Grafo Dirigido
Algoritmo SCC
T
•• G
GT éé transposto
transposto de
de um
um grafo
grafo dirigiro:
dirigiro:
–– G
GTT == (V,
(V, EETT),), EETT == {(u,
{(u, v)
v) :: (v,
(v, u)
u) ∈∈ E}.
E}.
T
–– G
G com
com todos
todos os
os arcos
arcos revertidos.
revertidos.
GT éé G
r
s
r
SCC(G)
DFS(G)
Calcula GT
DFS(GT)
Saída: os arcos de árvore formam SCCs
s
G
T
G
v
w
v
Teoria dos Grafos
w
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Exemplo Grafo de SCCs
r
v
Teoria dos Grafos
s
w
t
x
Passo 1: Aplicar DFS
u
y
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
r
s
t
u
13/14
11/16
1/10
8/9
12/15
3/4
2/7
5/6
v
w
x
y
© Jorge Figueiredo, DSC/UFCG
4
Passo 2: Calcular GT
Passo 3: DFS de GT
r
s
t
u
r
s
t
u
v
w
x
y
v
w
x
y
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Passo 3: DFS de GT
Passo 3: DFS de GT
r
s
t
u
r
s
t
u
v
w
x
y
v
w
x
y
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Passo 3: DFS de GT
Teoria dos Grafos
Passo 3: DFS de GT
r
s
t
u
r
s
t
u
v
w
x
y
v
w
x
y
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
5
Passo 3: DFS de GT
Passo 3: DFS de GT
r
s
t
u
r
s
t
u
v
w
x
y
v
w
x
y
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Teoria dos Grafos
© Jorge Figueiredo, DSC/UFCG
Passo 4: Componentes de GT
rsv
ut
xw
Teoria dos Grafos
y
© Jorge Figueiredo, DSC/UFCG
6