Avaliação de Oscilações de Tensão Devido à Partida de Motores

1
Avaliação de Oscilações de Tensão
Devido à Partida de Motores Usando
Método de Fluxo de Potência
César A. Portolann, Géremi G. Dranka, Jean-Marc S. Lafay, Diana Martinello
Universidade Tecnológica Federal do Paraná (UTFPR)

Resumo—Este trabalho aborda a aplicação das técnicas de
estudo de fluxo de potência, na avaliação de oscilações de tensão
originadas na partida de motores elétricos de indução. Diferente
da técnica comum baseada no divisor de tensão, este método
permite obter simultaneamente as intensidades das oscilações em
todas as barras da rede elétrica considerada. Além de verificar se
as oscilações estão dentro da tolerância, o método facilita a
escolha da chave de partida mais adequada. Esse método foi
aplicado a uma rede elétrica, a fim de se verificar a sua eficiência
para duas situações distintas.
Palavras-chaves — Estudo de fluxo de potência, Oscilações de
tensão, Partida de motores, Sistemas elétricos industriais.
I. INTRODUÇÃO
Muitos problemas de oscilações de tensão em sistemas
elétricos industriais são devidos à partida de motores elétricos.
É bem conhecido que as variações originadas destes eventos
podem ser reduzidas, por exemplo, pela redução das
impedâncias de rede ou principalmente pela utilização de
chaves de partida. Estes últimos métodos usados para
minimizar os afundamentos de tensão se baseiam no fato que
durante a partida um motor absorve uma corrente proporcional
à tensão terminal, e isso por sua vez reflete em menores
variações de tensão na rede.
Os estudos de partida de motor podem ser usados para
comprovar a eficiência das chaves de partida, para o problema
de variação de tensão. Uma maneira de verificar a amplitude
de um afundamento de tensão devido à partida de motor, é
assegurar que as máximas variações instantâneas que ocorrem
C. A. Portolann é Professor do Curso de Engenharia Elétrica da
Universidade Tecnológica Federal do Paraná – UTFPR (Campus Pato
Branco), Pato Branco, PR. (e-mail: portolann@ utfpr.edu.br);
G. Dranka é acadêmico do Curso de Engenharia Elétrica da UTFPR
(Campus
Pato
Branco),
Pato
Branco,
PR.
(e-mail:
[email protected]);
Jean-Marc Lafay é Professor do Curso de Engenharia Mecânica, Diretor
de Ensino e Coordenador do Grupo de Estudos em Energias Renováveis da
Universidade Tecnológica Federal do Paraná – UTFPR (Campus Pato
Branco), Pato Branco, PR. (e-mail: [email protected]);
D. Martinello é acadêmica do Curso de Engenharia Elétrica da UTFPR
(Campus
Pato
Branco),
Pato
Branco,
PR.
(e-mail:
[email protected]);
G. Muller (e-mail: [email protected]) é gerente geral do Britador
Hobi (Vitorino, PR) e, acadêmico do Curso de Tecnologia em Manutenção
Industrial da UTFPR (Campus Pato Branco), Pato Branco, PR.
Gilmar Muller
Mineradora Hobi
nas tensões de barra de um sistema elétrico, estejam dentro de
níveis aceitáveis [1]. Isto pode ser efetuado examinando alguns
estados da rede elétrica, no caso os módulos das tensões,
somente no instante crítico da partida do motor, ou seja, no
nível mais baixo da tensão. Por meio da modelagem adequada
da rede elétrica e do motor que irá partir, esse tipo de estudo
pode ser desenvolvido por alguns métodos de cálculo. Por
outro lado, percebe-se que em geral, não existem publicações
técnicas que tratem do problema de forma ampla e formal, que
permita calcular as oscilações de tensão na partida de motores
em todas as barras da rede elétrica considerada, sobretudo,
quando se considera sistemas industriais de grande porte com
vários alimentadores. Atualmente o que se faz é calcular as
quedas de tensão somente no alimentador do motor,
desprezando-se a influência da partida em outras partes do
sistema elétrico.
Este estudo tem por objetivo apresentar e explorar o
método de fluxo de potência que (i) estabelece as oscilações
de tensão em todas as barras de um sistema elétrico, não
apenas na barra do motor que irá partir, mas também em todas
as outras; e (ii) facilita a escolha da chave de partida mais
adequada, de tal forma que ela garanta que as oscilações de
tensão em todas as barras fiquem dentro da tolerância
estabelecida.
O artigo está organizado basicamente como se segue.
Depois da introdução, na seção II é visto sucintamente a causa
de oscilações de tensão devido à partida de motor, bem como
o princípio de ação das chaves de partida. A seção III comenta
resumidamente um dos vários métodos de análise de fluxo de
potência que podem ser utilizados no levantamento das
oscilações. Na seção IV são mostrados os resultados da
aplicação em uma rede elétrica. Na sequência são apresentadas
as conclusões.
II. OSCILAÇÕES DE TENSÃO DEVIDAS ÀS PARTIDAS
DE MOTORES
Esta seção tem como objetivo revisar sucintamente a razão
das oscilações de tensão que são originadas pela partida de
motores elétricos, bem como a ação elementar das chaves de
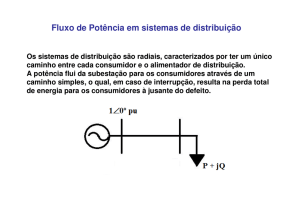
partida. O circuito representado na Fig. 1 consiste de uma
seção de rede elétrica com duas barras, onde a barra 2 contém
uma carga.
2
E
vez conduz a
aproximando-a
corrente I para
diferença entre
V
Z = R + jX
1
I
I
2
S = P + jQ
um aumento na amplitude da tensão V,
do módulo da tensão E. Com a redução da
I’, a tensão passa de V para V’, reduzindo a
E e V . De (1) e (3), obtém-se:
Fig. 1. Representação de um ramal elétrico de duas barras.
Utilizando-se o equivalente Thèvenin do circuito, pode-se
estabelecer as equações necessárias. Na ausência de um
controle em malha fechada, a tensão sobre a carga varia com a
impedância de rede e, com a própria carga. Essa variação será
conforme a equação (1).
V  E - V  ZI
(1)
No caso, E, V, Z e I, são respectivamente, a tensão na barra
à montante, tensão na barra à jusante, impedância e corrente da
rede. Com algumas manipulações algébricas, que podem ser
verificadas em [2], é estabelecida a conhecida expressão para
ΔV :
( RP  XQ)
( XP - RQ)
(2)
V 
 j
V*
V*
Adotando V  V 0o , V *  V 0o  V , resulta,
E  V  V
(4)
E 2  (V  VR )2  (VX )2
(5)
E 2  (V 
RP  XQ 2
XP - RQ 2
)  (
)
V
V
(6)
Depois das manipulações algébricas necessárias, uma
expressão geral resultante será [3]:


V 2   2RI cos   2 XIsen V  R 2 I 2  X 2 I 2 - E 2  0 (7)
Esta equação é particularmente importante porque mostra o
comportamento da tensão na barra à jusante, como função de
várias grandezas: tensão na barra à montante, amplitude da
corrente, fator de potência e impedância da rede elétrica.
Consequentemente ilustra as causas dos afundamentos de
tensão.
III. TÉCNICA DE ESTUDO DE FLUXO DE POTÊNCIA
V  VR  jVX
(3)
A. Generalidades
Esta expressão mostra que a tensão varia com uma
componente ΔVR em fase com V e com uma componente
ΔVX , em quadratura. A relação entre o módulo de tensão entre
duas barras de uma rede, e o fluxo de potência (ativo e
reativo), é dada pela expressão de ΔVR . O ângulo de potência
para essa transmissão é proporcional à equação de ΔVX . Na
Fig. 2 é ilustrada essa relação, onde φc é o ângulo de carga ou
de fator de potência.
Fig. 2. Diagrama fasorial, com evidência para a contribuição de uma chave de
partida.
Tanto o módulo como a fase de V, com relação à tensão E,
são funções da amplitude e fase da corrente de carga, ou em
outras palavras, a variação de tensão depende de ambas as
potências, ativa e reativa da carga, além dos parâmetros da
rede. Sob a ótica de que uma chave de partida adiciona uma
impedância à impedância de rotor bloqueado, e
consequentemente reduz a potência de rotor bloqueado, com o
auxílio da Fig. 2, pode ser visto que uma redução na corrente
de partida promove um alívio na corrente da rede, que por sua
No estudo requerido, o interesse são os valores máximos de
variação de tensão, somente no instante de tempo crítico da
partida do motor, que a norma técnica estabelece como 10%
da tensão nominal. O estudo para se obter esses valores
particulares que caracterizam o pior momento do referido
evento, pode ser considerado como uma “fotografia” das
amplitudes das tensões de barra.
Com respeito às relações matemáticas, um método clássico
para resolver as tensões de barra na partida de motor é o
método da impedância, que essencialmente envolve reduções
do sistema a um único alimentador ou rede elétrica, e é
aplicado o princípio do divisor de tensão [4]. A tensão em
qualquer barra do sistema é obtida, multiplicando a tensão
conhecida da barra de interligação, pela relação da impedância
do ponto ou barra considerada pela impedância total do
circuito. O método da impedância é indicado em situações
onde a análise deve ser feita para um único alimentador, ou
uma rede elétrica com poucos alimentadores. Se for aplicado a
um sistema mais complexo, exige uma manipulação algébrica
onerosa. Esta técnica basicamente requer dados da impedância
de rotor bloqueado.
Uma técnica alternativa ao método da impedância, e que é
motivo deste trabalho é o método de solução de fluxo de
potência [5]. Ele é baseado na matriz de admitâncias de barras,
e mostra de forma natural, as tensões (e consequentemente as
oscilações) em todas as barras, permitindo a avaliação não só
da barra onde está conectado o motor de interesse (que irá
3
partir), mas em todas as outras, conduzindo a uma análise
completa. Este método, por sua vez, é desenvolvido admitindo
que o motor que vai partir se comporta como uma carga de
potência constante, a potência de rotor bloqueado. Dessa
forma o resultado do cálculo de fluxo de potência são as
diversas tensões de barra durante a partida.
Para envolver as chaves de partida, os dois métodos exigem
que sejam levantadas respectivamente a impedância e a
potência equivalente (vistas pela fonte) de rotor bloqueado,
para cada tipo de chave.
existam outros motores já em funcionamento no sistema,
consideram-se os valores nominais de regime permanente. As
simulações que serão realizadas servem para mostrar a
eficiência do método considerando duas situações distintas. No
entanto, se necessário pode-se considerar infinitas
possibilidades, ou seja, partindo um ou mais motores,
incluindo ou retirando cargas do sistema, e ainda pode
fornecer resultados caso existam mais fontes geradoras dentro
do sistema.
IV. APLICAÇÃO A UM SISTEMA ELÉTRICO
INDUSTRIAL
B. Método de estudo de fluxo de potência de Newton-Raphson
Uma das ferramentas numéricas mais utilizadas, para a
solução de problemas envolvendo fluxo de potência é o
método de Newton-Raphson [6]. Neste método um conjunto
de equações deve ser resolvido para calcular os módulos e
ângulos das tensões de barra (e posteriormente os fluxos na
rede elétrica). Os termos ΔP e ΔQ representam as diferenças
de potência ativa e reativa em certa barra, pra cada nova
interação entre as variáveis. Essas diferenças são reduzidas até
uma tolerância pré-estabelecida para obter uma solução para o
fluxo de potência. Um conjunto de ângulos de fase e módulos
A. Generalidades
Para a avaliação da ferramenta proposta, a mesma é
aplicada em duas situações particulares, durante a operação de
uma mineradora (britador), cujo sistema elétrico está
representado de modo simplificado na Fig. 3. Os dois
transformadores que conectam as máquinas do britador à rede
têm as relações de transformação de 13,8 kV/380V, e
capacidade individual de 500 KVA.
9
T
de tensões de barras δo V o  satisfaz as equações de fluxo
de potência quando a potência injetada em uma barra j é P jo e
Qjo. As equações (8) e (9) são obtidas pela expansão das
funções Pj e Qj em séries de Taylor nas vizinhanças de
3
Q j =
δ1
Q j
δ1
δ1  ...
δ1  ...
Pj
V1
V1  ...
Q j
V1
(8)
4
T2
Subestação COPEL
Pato Branco
ZT1,2=0.0160 +
j0.0800 pu
5
C9
Z46=0.0048 +
j0.0086 Ω
6
Z58=0.0015 +
j0.0032 Ω
8
Z47=0.0015 +
j0.0018 Ω
Motor 150 cv C6
7
Dois motores
250 cv
C8
Motor 200 cv C7
Fig. 3. Esquema simplificado do sistema elétrico do britador.
B. Situação 1
V1  ...
(9)
Onde ΔPj e ΔQj são respectivamente as variações
requeridas nas potências ativas e reativas injetadas na barra j.
 P
 P   δ
 Q  =  Q
  
 δ
Z12=8.4900 +
j6.6080 Ω
Z23=00.0178 +
j0.0139 Ω
T1
Usina de asfalto
δo Vo  e desprezando-se os termos de ordem maior ou igual


a dois, para linearizar as equações. A equação (10) é obtida
reescrevendo um conjunto de equações similares a (8) e (9)
para todas as barras, exceto para a barra “swing” e,
representando na forma matricial se tem:
Pj
1
22 Km
Z29=0.1273 +
j0.0991 Ω
Outros
consumidores
T
Pj =
2
300 m
P 
V   δ 

Q   V 
V 
Nessa primeira análise, considera-se que um dos motores de
250 cv deverá partir, na barra 8, considerando que a maior
parte das cargas do sistema está ligada, exceto o motor e as
cargas da barra 6. Na Tabela I são mostradas as tensões de
barras resultantes da partida do referido motor.
TABELA I.
AMPLITUDES DAS TENSÕES DE BARRA (P.U. VOLT)
(10)
C. Contribuições metodológicas
O método de solução proposto neste trabalho permite a
obtenção das oscilações de tensão em cada barra da rede tanto
para sistemas radiais como malhados. Como o interesse são as
oscilações máximas durante a partida, utiliza-se o valor de
potência de rotor bloqueado do motor que está partindo. Caso
Barra
1
2
3
4
5
6
7
8
9
Direta
1.0000
0.8618
0.8615
0.8357
0.6752
0.8357
0.8294
0.6181
0.8618
Y-Δ
1.0000
0.9374
0.9373
0.9137
0.8761
0.9137
0.9080
0.8566
0.9374
Compensadora
1.0000
0.9433
0.9431
0.9197
0.8918
0.9197
0.9141
0.8753
0.9433
Soft-starter
1.0000
0.9520
0.9519
0.9288
0.9153
0.9288
0.9231
0.9032
0.9520
4
Estas tensões são para vários tipos de métodos de partida,
obtidas através de estudo de fluxo de potência aplicado à rede
elétrica considerada. As potências fornecidas pela subestação,
para cada tipo de chave de partida, bem como os valores de
fluxos e perdas, foram omitidas, visto que o interesse são as
tensões e suas oscilações.
Os valores mostrados na Tabela I foram plotados,
resultando nas curvas da Fig. 4. Pode ser visto, que a presença
das chaves de partida faz com que os níveis de tensão se
mantenham melhores durante o evento de partida do motor,
enquanto que na ausência das chaves de partida, as tensões
caem para níveis inaceitáveis. O limite mínimo préestabelecido para as tensões de barra é de 90% da tensão
nominal [7]. Assim, este limite é violado para os casos de
partida direta, Y-Δ e compensadora. Quando é utilizada uma
chave de partida suave, as tensões mínimas permanecem
dentro da tolerância. Para este caso, supõe-se que o ajuste do
ângulo de disparo dos tiristores é feito de tal forma que a
tensão inicial seja 35% da nominal, e o torque resultante,
embora reduzido, é ainda suficiente para colocar o motor (em
vazio) em movimento.
V  %  
Barra
1
2
3
4
5
6
7
8
9
0.95
35
0.9
30
0.85
0.8
0.75
0.7
3
Soft-starter
0
4.7969
4.8070
7.1242
8.4684
7.1242
7.6859
9.6759
4.7969
Direta
Estrela-Triângulo
Compensadora
Soft-Starter
25
20
15
10
Direta
Estrela-Triângulo
Compensadora
Soft-Starter
2
TABELA II.
OSCILAÇÕES DE TENSÕES DE BARRA (%)
Direta
Y-Δ
Compensadora
0
0
0
13.8189
6.2591
5.6735
13.8475
6.2722
5.6854
16.4306
8.6285
8.0259
32.4754
12.3935
10.8231
16.4306
8.6285
8.0259
17.0558
9.1997
8.5932
38.1884
14.3404
12.4743
13.8189
6.2591
5.6735
Oscilações de Tensões nas barras na partida de um motor de 250 CV
40
Oscilações de Tensão (%)
Tensão (p.u. Volt)
Tensões nas barras na partida de um motor de 250 CV
1
(11)
Onde V1 representa as tensões iniciais em cada barra e Vi a
tensão durante a partida do motor.
Conforme esperado, com a presença das chaves de partida,
as oscilações são menores.
1
0.65
V1 - Vi
100
Vi
5
4
5
Barras
6
7
8
0
9
Fig. 4. Módulos de tensões durante a partida de motor.
Uma maneira alternativa de avaliar os afundamentos de
tensão na partida de motores é obterem-se os valores das
oscilações de tensão resultantes em cada barra. No caso, elas
se referem ao valor de tensão que se reduz em cada ponto do
alimentador, particularmente nas barras, em comparação à
tensão nominal, considerada como 1 p.u., como ilustrado na
Fig. 5. São desejáveis pelo consumidor que essas variações
sejam as mínimas possíveis, porque elas podem levar a carga,
bem como os dispositivos de comando e proteção a operações
indesejáveis. Também, podem contribuir para reduzir o
conceito da companhia perante os consumidores vizinhos [8].
As oscilações de tensão para as barras da rede em questão são
mostradas na Tabela II para os diferentes tipos de chaves de
partida. Os valores estão dados em termos de oscilação
percentual, conforme a expressão (11):
1
2
3
4
5
Barras
6
7
8
9
Fig. 5. Oscilações de tensão durante a partida do motor de 250 CV.
C. Situação 2
Considera-se, neste caso, a partida simultânea dos dois
motores de 250 cv na barra 8.
TABELA III.
AMPLITUDES DAS TENSÕES DE BARRA (P.U. VOLT)
Barra
1
2
3
4
5
6
7
8
9
Direta
1.0000
0.7381
0.7379
0.7354
0.5352
0.7354
0.7354
0.4180
0.7381
Y-Δ
1.0000
0.9592
0.9591
0.9591
0.8883
0.9591
0.9591
0.8671
0.9592
Compensadora
1.0000
0.9704
0.9703
0.9703
0.9188
0.9703
0.9703
0.9034
0.9704
Soft-starter
1.0000
0.9863
0.9863
0.9863
0.9624
0.9863
0.9863
0.9553
0.9863
5
Tensões nas barras na partida de dois motores de 250 CV
1
Tensão (p.u. Volt)
0.9
0.8
0.7
0.6
Direta
Estrela-Triângulo
Compensadora
Soft-Starter
0.5
0.4
1
2
3
4
5
Barras
6
7
8
9
Fig. 6. Módulos de tensões durante a partida dos motores.
Em relação às oscilações de tensão os valores são
mostrados na tabela para cada chave de partida, e dados em
termos de oscilação percentual.
Barra
1
2
3
4
5
6
7
8
9
TABELA IV.
OSCILAÇÕES DE TENSÕES DE BARRA (%)
Direta
Y-Δ
Compensadora
0
0
0
26.1939
4.0834
2.9639
26.2120
4.0919
2.9701
26.4629
4.0919
2.9701
46.4834
11.1741
8.1196
26.4629
4.0919
2.9701
26.4629
4.0919
2.9701
58.1958
13.2922
9.6596
26.1939
4.0834
2.9639
Oscilações de Tensões nas barras na partida de dois motores de 250 CV
60
Além disso, mostram-se na Fig. 7 as oscilações de tensão
quando da partida de ambos os motores de 250 cv.
40
30
20
10
0
1
2
3
4
5
Barras
6
7
8
9
Fig. 7. Oscilações de tensão durante a partida dos motores de 250 CV.
V. CONCLUSÕES
O método baseado em estudo de fluxo de potência adaptado
para obter afundamentos de tensão em redes elétricas,
originadas da partida de motor, foi apresentado. Ao contrário
do método clássico do divisor de tensão que é limitado e
trabalhoso para sistemas de grande porte, o método
apresentado neste trabalho contribui significativamente para
simplificar a avaliação das oscilações de tensão fornecendo
resultados que mostram claramente quais barras sofrem com
variações de tensão fora da tolerância, bastando inserir no
programa de simulação os valores dos parâmetros dos
motores, geradores, cargas e das linhas de interligação entre as
barras.
Também, a técnica explorada se constitui numa ferramenta
importante na escolha da chave mais adequada, dando suporte
para a elaboração de medidas corretivas, como a substituição
de chaves de partida ineficientes, troca de cabos, mudança no
nível de tensão, etc.
REFERÊNCIAS
[1]
[2]
Soft-starter
0
1.3700
1.3729
1.3729
3.7590
1.3729
1.3729
4.4726
1.3700
Direta
Estrela-Triângulo
Compensadora
Soft-Starter
50
Oscilações de Tensão (%)
Supõe-se que todas as outras cargas (inclusive os motores
de 150 cv e 250 cv) estão desligadas. Na Tabela III são
mostradas as tensões de barras resultantes obtidas através de
estudo de fluxo de potência aplicado à rede elétrica
considerada. As potências fornecidas pela subestação, para
cada tipo de chave de partida, bem como os valores de fluxos e
perdas, aqui também foram omitidos.
Os valores mostrados na Tabela III resultam nas curvas da
Fig. 6. Pode ser visto que a presença das chaves de partida faz
com que os níveis de tensão se mantenham melhores durante o
evento de partida do motor. Como o limite máximo de
oscilação é 10% em relação à tensão nominal, ele seria violado
para os casos de partida direta e Y-Δ, enquanto que para
partida compensadora a queda na barra em que os motores
estão localizados é próxima do limite, mas ainda menor.
Quando se considera a utilização de uma chave de partida
suave, as tensões mínimas são extremamente toleráveis, sendo
menores que 5%, lembrando que o ajuste do ângulo de disparo
dos tiristores é feito de tal forma que a tensão inicial seja 35%
da nominal.
[3]
[4]
[5]
[6]
[7]
[8]
Willians, A. J., Griffith, M. S., Evaluating the Effects of Motor Starting
on Industrial and Commercial Power Systems, Ieee Trans. on Industry
Applications, Vol. IA-14, No. 4, July/Ago. 1978.
Miller, T. J. E., Reactive Power Control In Electric Systems, Livro,
Editora John Wiley & Sons, New York, Eua, 1982.
Portolann, C. A., Campagnolo J. M., Um Estudo sobre a Contribuição
de Alívios de Carga na Regulação de Tensão em Redes Fracas, VIII
Congresso Brasileiro Sobre Qualidade Da Energia Elétrica (Cbqee),
Santos, Ago. 2007.
Mamede filho, J., Instalações Elétricas Industriais. Rio de Janeiro: 2010.
Portolann, C. A., Kolzer, J. F., Lafay, J-M. S., Machado, M., Canzi, A.
L., Influência de Pequena Central Hidrelétrica na Regulação de Tensão
da Forcel, XXI Seminário Nacional de Produção e Transmissão de
Energia Elétrica (XXI SNPTEE), Florianópolis, 23 a 26 de outubro de
2011.
Kagan, N., Oliveira, C. C. B., Robba, E. J., Introdução aos Sistemas de
Distribuição de Energia Elétrica, Livro, 1ª Edição, Ed. Blucher, São
Paulo, 2005.
Deckmann, S. M., Pomilio, J. A., Avaliação da Qualidade da Energia
Elétrica, Publicação interna, LCEE-DSCE-FEEC-UNICAMP.
Franchi, C. M., Acionamentos Elétricos, Livro, 2ª. Edição, Editora
Erica, São Paulo, SP, 2007.