Resumo - Variáveis aleatórias e modelos teóricos

Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
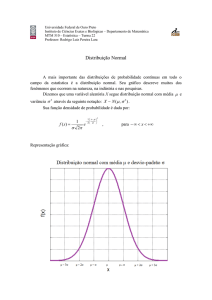
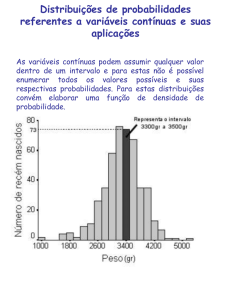
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Variáveis aleatórias e modelos teóricos unidimensionais
1
Noção de variável aleatória unidimensional
Ao descrever o espaço amostral de uma experiência, não especificamos que
um resultado individual tem que ser necessariamente um número. De facto,
nem sempre a experimentação estatística tem resultados numéricos.
Exemplo 1.1.
• Uma peça pode ser defeituosa ou não ser defeituosa;
• Ao observar a temperatura durante 24 horas, podemos registar a curva
traçada pelo aparelho de medição em vez dos valores observados.
Contudo, a maioria das vezes estamos interessados em resultados numéricos. De facto, em muitas situações concretas atribuímos um número real x
a cada resultado s do espaço amostral S.
Definição 1.1. Uma variável aleatória, v. a., X é uma função que associa
um número real x a cada resultado s do espaço amostral S.
Variável Aleatória
X
S
s
Espaço Amostral
• A cada resultado s P S corresponde exactamente um valor x “ X psq.
A diferentes valores de s pode corresponder o mesmo valor x de X;
• Frequentemente, o espaço amostral original já constitui a característica
numérica que pretendemos estudar e cujo valor registamos. Neste caso,
X psq “ s é a função identidade;
• É evidente que nem toda a função imaginável pode ser considerada
uma variável aleatória. Um requisito (embora não seja o mais geral)
é que, para todo o numerável real x, o evento X psq “ x, e para todo
o intervalo I, o evento X psq P I, têm-se probabilidades bem definidas,
consistentes com os axiomas básicos.
Exemplo 1.2. Consideremos o espaço amostral associado à experiência aleatória de lançar duas moedas ao ar: S “ tpc, cq ; pc, eq ; pe, cq ; pe, equ.
Se definirmos a variável aleatória X - “número de caras obtidas nas duas
moedas”, tem-se X pc, cq “ 2, X pc, eq “ X pe, cq “ 1 e X pe, eq “ 0.
As variáveis aleatórias podem ser classificadas em discretas ou contínuas.
Definição 1.2. Uma variável aleatória X é discreta se o conjunto de valores
possíveis de X for finito ou infinito numerável.
Definição 1.3. Uma variável aleatória X é contínua se pode tomar qualquer
valor de um intervalo ou de uma colecção de intervalos.
Na maior parte dos problemas práticos:
S'
• as variáveis aleatórias discretas representam dados contáveis ou numeráveis, por exemplo, o número de peças avariadas, o número de acidentes por ano ou o número de nascimentos;
x =X(s)
• as variáveis aleatórias contínuas representam dados medidos, por exemplo, o tempo, a distância, o peso ou a altura.
Recta Real
Exemplo 1.3. Considerem-se as seguintes situações. Para cada caso, definese e classifica-se a variável aleatória de interesse e indica-se a sua gama de
valores possíveis.
Observação 1.1.
(a) Contam-se as partículas emitidas por uma fonte radioactiva durante
um intervalo de tempo.
• S (domínio) é o espaço amostral original;
• S 1 (contradomínio) é o espaço amostral associado à característica numérica que pretendemos estudar;
X - “número de partículas radioactivas contadas”, é uma variável aleatória discreta e S 1 “ t0, 1, 2, 3, . . .u “ N0 .
• Usamos uma letra maiúscula, por exemplo X, para designar uma variável aleatória e uma letra minúscula, por exemplo x, para designar
uma das suas concretizações;
(b) Observa-se o tempo entre avarias de uma máquina em funcionamento
numa fábrica.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
1/62
X - “tempo entre as avarias” é uma variável aleatória contínua e S 1 “
r0, `8r.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
2/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
1.1
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Cálculo de probabilidades através de variáveis aleatórias
Como a cada acontecimento definido em S se faz corresponder um número
real x, o objectivo é agora calcular as probabilidades associadas aos valores
assumidos pela variável aleatória X.
2
Variáveis aleatórias unidimensionais discretas
Quando a variável aleatória é discreta, o conjunto de possibilidades para X
é finito ou infinito, mas numerável.
Exemplo 2.1. Considerem-se as seguintes variáveis aleatórias:
• X - “número de veículos que passam na via verde de uma determinada
auto-estrada por dia”;
• Y - “número de chamadas, por hora, num determinado telefone”;
• Z - “número de coroas que obtenho quando lanço uma moeda ao ar
duas vezes seguidas”;
• W - “número de defeitos por m de tecido”.
2
2.1
Função massa de probabilidade
A função massa de probabilidade da variável aleatória X é uma função f que
associa a cada valor possível de X a sua probabilidade f pxq “ P rX “ xs e
tem as seguintes propriedades:
onde pi é a probabilidade
da variável X assumir o valor xi , i “ 1, . . . , n,
ř
com pi ě 0 e ni“1 pi “ 1. Assumindo que a variável X assume os valores
x1 , . . . , xn a função de probabilidade pode também ser escrita duma das
seguintes formas:
xi
f pxi q
• caso n seja finito,
• caso n seja infinito,
soma 1.
i“1
i“1
P pXq “ pp1 , . . . , pn q .
Exemplo 2.2. Num restaurante típico, o pessoal da cozinha é constituído
por três homens e três mulheres. O gerente queria atribuir a responsabilidade por um banquete, que iria ter lugar no fim-de-semana seguinte, a dois
elementos dessa equipa, pelo que, para ser imparcial resolveu seleccioná-los
aleatoriamente.
Consideremos a variável aleatória X - “número de mulheres nessa amostra aleatória”.
• P rX “ 0s “
3C ˆ3C
0
2
6C
2
“ 51 ;
• P rX “ 1s “
3C ˆ3C
1
1
6C
2
“ 53 ;
• P rX “ 2s “
3C ˆ3C
2
0
6C
2
“ 51 .
Tem-se assim a função de probabilidade e a respectiva representação gráfica:
xi
0
1
2
f pxi q
1
5
3
5
1
5
f pxi q terá de ser uma série convergente de
Tem-se então a função de probabilidade:
"
pi , se x “ xi
f pxq “
,
0 , se x ‰ xi
i “ 1, . . . , n,
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
xn
pn
Podemos dizer que DX “ tx1 , . . . , xn u representa o domínio da variável X.
f pxi q “ 1;
řn
¨¨¨
¨¨¨
ou
• f pxq ě 0;
řn
x1
p1
3/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
4/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
• P rx1 ď X ă x2 s “ F px2 q ´ F px1 q ´ P rX “ x2 s ` P rX “ x1 s, @x1 , x2 ,
com x2 ą x1 .
f (x )
3
5
Exemplo 2.3. Considerando a variável aleatória do exemplo 2.2, podemos
obter a função de distribuição:
$
0 , se x ă 0
’
’
& 1
, se 0 ď x ă 1
5
F pxq “
.
4
, se 1 ď x ă 2
’
5
’
%
1 , se x ě 2
2
5
1
5
0
2.2
1
2
x
Função de distribuição ou função cumulativa
F (x )
A função de distribuição possibilita calcular a probabilidade de X assumir
um conjunto de valores. Considerando X uma variável aleatória, chama-se
função de distribuição de X, a uma função F pxq que é igual à probabilidade
de X tomar todos os valores menores ou iguais a x.
A função de distribuição no ponto x é definida por:
ÿ
F pxq “ P rX ď xs “
f pxi q ,
1
4
5
3
5
2
5
xi ďx
onde xi toma todos os valores possíveis da variável aleatória X não superiores
a x.
Esta função tem domínio R, conjunto de chegada r0, 1s, e satisfaz as
seguintes propriedades:
• 0 ď F pxq ď 1, @x P R;
1
5
0
2.3
• F px2 q ě F px1 q, @x1 , x2 , com x2 ą x1 ;
• limxÑ´8 F pxq “ 0 e limxÑ`8 F pxq “ 1;
1
2
x
Parâmetros das variáveis aleatórias unidimensionais
discretas
Quando temos os valores que uma variável aleatória pode tomar e a respectiva
função de probabilidade, temos definida uma distribuição de probabilidade.
Uma distribuição de probabilidade estuda-se através de:
• F pxq é contínua à direita, limxÑx`0 F pxq “ F px0 q;
• F pxq é descontínua à esquerda nos pontos em que a probabilidade é
diferente de zero, limxÑx´0 F pxq ‰ F px0 q, para P rX “ x0 s ‰ 0;
• P rX “ x0 s “ F px0 q ´ limxÑx´0 F pxq, @x0 P R;
• parâmetros, momentos ou parâmetros de ordem;
• relativamente à localização ou tendência central - valor médio, moda e
mediana;
• P rx1 ă X ă x2 s “ F px2 q ´ F px1 q ´ P rX “ x2 s, @x1 , x2 , com x2 ą x1 ;
• quanto à dispersão - variância, desvio padrão e desvio médio;
• P rx1 ď X ď x2 s “ F px2 q ´ F px1 q ` P rX “ x1 s, @x1 , x2 , com x2 ą x1 ;
• quanto à assimetria - parâmetro γ1 ;
• P rx1 ă X ď x2 s “ F px2 q ´ F px1 q, @x1 , x2 , com x2 ą x1 ;
• quanto ao achatamento ou curtose - parâmetro β3 .
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
5/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
6/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
2.4
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Momentos
2.6
Podemos definir os seguintes momentos:
Mediana
É um parâmetro de ordem que serve para localizar a distribuição ao centro:
“ ‰
• momentos de ordem k em relação à origem, E X k , com k inteiro
positivo:
n
“ ‰ ÿ
E Xk “
xki f pxi q ;
i“1
• momentos
de ordem
k em relação à média ou momento central de ordem
”
ı
k, E pX ´ µqk , com k inteiro positivo:
Me “ min tx P R : F pxq ě 0, 5u .
Exemplo 2.5. Seja X a variável que descreve o número de “coroas” que se
obtêm quando se lançam duas moedas ao ar e se verifica a face que fica virada
para cima. Qual a mediana da variável aleatória de X?
A função de probabilidade associada a esta variável aleatória (utilizando
o conceito clássico de probabilidade) é dada por:
n
ı ÿ
”
pxi ´ µqk f pxi q .
E pX ´ µqk “
2.5
0
xi
f pxi q
i“1
Valor médio, valor esperado ou esperança matemática
` 1 ˘2
2
“ 0, 25
2
1
`1˘ `1˘
2
2
2
“ 0, 5
` 1 ˘2
2
“ 0, 25
Temos que calcular, analiticamente, a função distribuição:
É o primeiro momento em relação à origem,
F p0q “ P rX ď 0s “ f p0q “ 0, 25;
E rXs “ µ.
O valor médio exprime-se em unidades de X. O valor médio indica o ponto
em torno do qual mais se concentram as probabilidades. Define-se do seguinte
modo:
n
ÿ
E rXs “
xi f pxi q .
F p1q “ P rX ď 1s “ f p0q ` f p1q “ 0, 25 ` 0, 5 “ 0, 75;
F p2q “ P rX ď 2s “ f p0q ` f p1q ` f p2q “ 0, 25 ` 0, 5 ` 0, 25 “ 1.
Assim,
$
’
’
&
0
0, 25
F pxq “
0, 75
’
’
%
1
i“1
Propriedades 2.1. Sendo X e Y duas variáveis aleatórias e k uma constante real, tem-se:
,
,
,
,
se
se
se
se
xă0
0ďxď1
1ďxď2
xě2
• E rkXs “ kE rXs;
e como se pode observar, a mediana é igual a 1, pois é o primeiro valor de
x a que corresponde um valor da função distribuição maior ou igual a 0, 5,
F pxq ě 0, 5.
• E rX ˘ Y s “ E rXs ˘ E rY s;
2.7
• E rXY s “ E rXs ˆ E rY s, se X e Y são independentes.
Seja X uma variável aleatória discreta, com função de distribuição F pxq e
p P r0, 1s. Chama-se quantil de probabilidade p ou quantil de ordem p da
variável aleatória X, ao valor
• E rks “ k;
Exemplo 2.4. Para a variável aleatória do exemplo 2.2, o valor médio é
dado por:
1
3
1
E rXs “ 0 ˆ ` 1 ˆ ` 2 ˆ “ 1,
5
5
5
concluindo-se que o número médio de mulheres escolhidas, entre cada dois
empregados seleccionados, é 1.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
7/62
Quantis
χp “ min tx P R : F pxq ě pu .
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
8/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Exemplo 2.7. Para a variável aleatória do exemplo 2.5, qual é a moda da
variável aleatória de X?
A função probabilidade é dada por:
Os quartis podem ser obtidos considerando:
• 1 quartil:
o
χ0,25 “ min tx P R : F pxq ě 0, 25u ;
xi
f pxi q
• 2 quartil ou mediana:
o
χ0,5 “ min tx P R : F pxq ě 0, 5u ;
0
0, 25
1
0, 5
2
0, 25
A moda de X é igual a 1, por ser o valor de x a que corresponde maior
probabilidade.
• 3o quartil:
χ0,75 “ min tx P R : F pxq ě 0, 75u .
Exemplo 2.6. Para a variável aleatória do exemplo 2.5, determine os quartis
da variável aleatória de X?
A função distribuição é dada por:
$
0
, se x ă 0
’
’
&
0, 25 , se 0 ď x ď 1
F pxq “
0, 75 , se 1 ď x ď 2
’
’
%
1
, se x ě 2
Os quartis são obtidos considerando:
• 1o quartil: χ0,25 “ min tx P R : F pxq ě 0, 25u “ 0;
2.9
Variância
O 2 momento em relação à média ou 2o momento central,
“
‰
E pX ´ µq2 “ V ar rXs “ σ 2 ,
o
é chamado de variância de X. Como a variância é uma quantidade de 2a
ordem, exprime-se em punidades de Xq2 . Seja X uma variável aleatória, a
2
variância de X representada por V ar rXs “ σX
“ σ 2 define-se por:
n
“
‰ ÿ
pxi ´ µq2 f pxi q .
V ar rXs “ E pX ´ µq2 “
i“1
Propriedades 2.2. Sendo X e Y duas variáveis aleatórias e k uma constante real, tem-se:
• 2o quartil ou mediana: χ0,5 “ min tx P R : F pxq ě 0, 5u “ 1;
• 3o quartil: χ0,75 “ min tx P R : F pxq ě 0, 75u “ 1.
• V ar rks “ 0;
Assim podemos dizer que cerca de 25% dos valores da distribuição do número
de “coroas” que se obtêm quando se lançam duas moedas ao ar e se verifica
a face que fica virada para cima, são inferiores a 0 e que cerca de 75% são
inferiores a 1. Podemos ainda referir que cerca de 75% dos valores da distribuição do número de “coroas” que se obtêm quando se lançam duas moedas
ao ar e se verifica a face que fica virada para cima, são superiores ou iguais
a 0 e que cerca de 25% são superiores ou iguais a 1.
• V ar rkXs “ k 2 V ar rXs;
• V ar rX ˘ Y s “ V ar rXs ` V ar rY s, se X e Y são independentes;
“
‰
• V ar rXs “ E pX ´ µq2 “ E rX 2 ´ 2µX ` µ2 s “ E rX 2 s ´ 2µ2 ` µ2 “
2
2
E rX s ´ E rXs , sendo
n
“ ‰ ÿ
E X2 “
x2i f pxi q .
i“1
2.8
Moda
Exemplo 2.8. Para a variável aleatória do exemplo 2.2, temos que:
É um parâmetro de ordem que é o valor ou valores de x, pois a distribuição
pode ter mais de uma moda, para os quais a função de probabilidade é
máxima.
No caso de uma distribuição discreta a moda é detectada de imediato e
é o valor xi para o qual f pxi q é maior.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
9/62
“ ‰
1
3
1
7
E X 2 “ 02 ˆ ` 12 ˆ ` 22 ˆ “ ,
5
5
5
5
obtendo-se a variância
“ ‰
2
7
V ar rXs “ E X 2 ´ E rXs2 “ ´ 12 “ .
5
5
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
10/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
2.10
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Sendo
Desvio padrão
O desvio padrão é a raiz quadrada da variância,
a
σ “ V ar rXs
E rXs “
e exprime-se em unidades de X. Observe-se que a variância e o desvio padrão
só assumem valores não negativos. Quanto menor for o valor do desvio padrão
maior é a concentração dos valores da variável em torno da média.
2.11
2.12
Desvio médio
Nas distribuições discretas temos:
Dm “ E r| X ´ µ |s “
n
ÿ
i“1
| xi ´ µ | f pxi q .
xi f pxi q “ 0 ˆ 0, 125 ` 1 ˆ 0, 375 ` 2 ˆ 0, 375 ` 3 ˆ 0, 125 “
tem-se
4
ÿ
i“1
| xi ´ µ | f pxi q “| 0 ´ 1, 5 | ˆ0, 125` | 1 ´ 1, 5 | ˆ0, 375 `
` | 2 ´ 1, 5 | ˆ0, 375` | 3 ´ 1, 5 | ˆ0, 125 “
Seja X uma variável aleatória. Ao quociente entre o desvio padrão e o valor
médio dá-se o nome de coeficiente de variação da variável aleatória X, Cv , e
obtém-se por:
σ
Cv “ ˆ 100%,
µ
mas isto não significa que é sempre inferior a 100%, pois pode ocasionalmente
ser superior. O coeficiente de variação é uma medida de dispersão relativa
(pois não depende das unidades da variável X), que permite analisar se os
dados se encontram mais ou menos dispersos em relação ao valor médio µ.
Uma das razões para usar o coeficiente de variação é o facto de não depender
das unidades em que X foi medida, pelo que pode ser usado para comparar
variáveis quanto à dispersão, quando estas têm unidades de medida diferentes
ou quando têm valores médios muito diferentes.
i“1
“ 0 ` 0, 375 ` 0, 75 ` 0, 375 “ 1, 5,
Dm “
Coeficiente de variação
4
ÿ
“ 1, 5 ˆ 0, 125 ` 0, 5 ˆ 0, 375 ` 0, 5 ˆ 0, 375 ` 1, 5 ˆ 0, 125 “
“ 0, 75.
2.13
Assimetria
As medidas de assimetria permitem analisar uma distribuição de probabilidade de acordo com as relações existentes entre a moda, a média e a mediana.
Uma distribuição de probabilidade diz-se simétrica quando a sua moda, média e mediana são iguais. Quando esta igualdade não se verifica, temos uma
distribuição assimétrica. Consideremos um eixo de referência traçado sobre
o valor da média da distribuição, o eixo de simetria. Quando a curva da
distribuição de probabilidade se afastar do referido eixo, esta terá um certo
grau de afastamento, que é considerado como uma assimetria da distribuição.
Sendo assim, podemos definir a assimetria como sendo o grau de afastamento
que uma distribuição apresenta em relação ao seu eixo de simetria. Este afastamento pode acontecer do lado esquerdo ou direito.
2
0, 375
3
0, 125
Moda
1
0, 375
Media na
Média
0
0, 125
Mo da
xi
f pxi q
Média
Mediana
Exemplo 2.9. Consideremos uma variável aleatória X e a respectiva função
probabilidade:
Média = Mediana = Moda
Calcule o desvio médio.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
11/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
12/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Como medida de assimetria temos o parâmetro:
“
‰
E pX ´ µq3
µ3
γ1 “ „b
ȷ3 “ 3 ,
σ
‰
“
E pX ´ µq2
com
Se:
2.14
Achatamento ou curtose
O achatamento ou curtose é uma medida que caracteriza o pico ou achatamento da distribuição de probabilidade. Podemos dizer que a curtose é o
grau de achatamento da distribuição de probabilidade. As medidas de achatamento ou curtose medem o grau de afunilamento ou de achatamento de
uma curva em relação à curva normal (curva de Gauss).
Como medida de achatamento temos o parâmetro:
“
‰
E pX ´ µq4
µ4
β3 “ „b
ȷ4 “ 4 ,
σ
“
2‰
E pX ´ µq
“
‰
“ ‰
“ ‰
µ3 “ E pX ´ µq3 “ E X 3 ´ 3E X 2 µ ` 2µ2 .
• γ1 ă 0 a distribuição é assimétrica negativa;
com
Se:
“
‰
“ ‰
“ ‰
“ ‰
µ4 “ E pX ´ µq4 “ E X 4 ´ 4E X 3 µ ` 6E X 2 µ2 ´ 3µ4 .
• β3 ă 3 a distribuição é platicúrtica (a distribuição é mais achatada que
a normal);
• γ1 “ 0 a distribuição é simétrica;
• β3 “ 3 a distribuição é mesocúrtica (o achatamento é igual ao da
normal);
• γ1 ą 0 a distribuição é assimétrica positiva.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
13/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
14/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
• β3 ą 3 a distribuição é leptocúrtica (a distribuição é menos achatada
que a normal).
3.1.1
Função de probabilidade
A função de probabilidade é dada por:
" 1
, se x “ i, i ` 1, . . . , j
f pxq “ j´i`1
.
0
, se x ‰ i, i ` 1, . . . , j
3.1.2
Valor médio, valor esperado ou esperança matemática
Se X segue uma distribuição uniforme discreta então:
E rXs “
Nota 2.1. 3 é o achatamento de uma distribuição normal. Este parâmetro limita-se a dizer se a distribuição é mais ou menos achatada do que a
distribuição normal.
3
Variância
Se X segue uma distribuição uniforme discreta então:
V ar rXs “
Modelos teóricos unidimensionais discretos
A utilização das funções que visam descrever a forma como se distribuem
as probabilidades, pelos diferentes resultados possíveis de uma determinada
variável, é relativamente simples. Contudo, a definição da sua expressão
matemática para uma variável aleatória específica é um processo bastante
complexo e trabalhoso, que requer um elevado conhecimento matemático.
Com o objectivo de tornar a aplicação das funções mais simples e acessível a
todos, foram construídos uma série de modelos para a forma como as probabilidades se distribuem pelos vários resultados da variável aleatória e que são
comummente designados por distribuições de probabilidade. Os contextos
reais são muito diversos, resultando numa grande diversidade de variáveis
aleatórias, no que diz respeito à forma como as probabilidades se distribuem
pelos resultados possíveis. Esta diversidade tem como consequência a existência de uma grande variedade de modelos de distribuição de probabilidade.
Iremos abordar os principais modelos.
3.1
3.1.3
(a) Determine a função de probabilidade de X;
1
f pxq “ P rX “ xs “ , x “ 1, . . . , 6,
6
portanto, a variável aleatória X segue uma distribuição uniforme discreta com n “ 6.
(b) Determine o valor esperado e a variância de X;
E rXs “
i`j
2
“
1`6
2
“ 3, 5 e V ar rXs “
15/62
pj´i`1q2 ´1
12
“
p6´1`1q2 ´1
12
“
35
.
12
(c) Num lançamento, qual a probabilidade de sair um número inferior a 3?
P rX ă 3s “ P rX “ 1s ` P rX “ 2s “
Os valores que a variável aleatória X pode assumir são os números inteiros
i, i ` 1, i ` 2, . . . , j ´ 1, j, com i ď j, e ocorrem com igual probabilidade. A
notação X „ Unif ormeDiscreta ti, . . . , ju indica que a variável aleatória X
tem distribuição uniforme discreta com parâmetros i e j.
C. Fernandes & P. Ramos
pj ´ i ` 1q2 ´ 1
.
12
Exemplo 3.1. Considere-se a experiência aleatória que consiste no lançamento de um dado. Seja X a variável aleatória que representa o valor da
face voltada para cima.
Distribuição uniforme discreta
Variáveis aleatórias e modelos teóricos unidimensionais
i`j
.
2
3.2
3.2.1
1
6
`
1
6
“ 13 .
Distribuição de Bernoulli
Provas de Bernoulli
Chama-se prova de Bernoulli a uma experiência aleatória que tem apenas
dois resultados possíveis: A - “sucesso” e A - “insucesso”. O sucesso ocorre
com probabilidade p e o insucesso com probabilidade 1 ´ p “ q.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
16/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
A variável aleatória X, com distribuição de Bernoulli, toma o valor x “ 1
se a experiência tiver sucesso e x “ 0 se a experiência tiver insucesso.
A notação X „ Bernoulli ppq indica que a variável aleatória X tem distribuição de Bernoulli com probabilidade p. A função de probabilidade é da
forma:
" x
p p1 ´ pq1´x , se x “ 0; 1
f pxq “
.
0
, se x ‰ 0; 1
3.2.2
Valor médio, valor esperado ou esperança matemática
E rXs “ p.
3.2.3
Variância
V ar rXs “ p p1 ´ pq .
3.2.4
Sucessão de provas de Bernoulli
Consiste num processo caracterizado por repetidas provas de Bernoulli, em
que se verificam as seguintes condições:
• a probabilidade de sucesso, p “ 23 , é a mesma em qualquer prova;
• a probabilidade de sucesso não é afectada pelo conhecimento do resultado obtido em lançamentos anteriores, pelo que as provas repetidas
são independentes.
3.3
Distribuição binomial
A distribuição binomial é uma generalização da distribuição de Bernoulli,
para o caso de n repetições independentes de uma experiência e portanto,
está associada a uma sucessão de provas de Bernoulli.
Esta distribuição utiliza-se para descrever o resultado de um determinado
número pnq de repetições de uma experiência aleatória (sempre nas mesmas
condições), com apenas dois resultados possíveis. A variável aleatória X vai
descrever o número de vezes em n, em que ocorre o acontecimento A (número
de sucessos) nas n provas de Bernoulli e escreve-se X „ Binomial pn, pq ou
X „ b pn, pq.
Supondo que A tem a probabilidade P rAs
“ ‰ “ p numa única prova, a
probabilidade da não ocorrência de A será P A “ q “ 1 ´ p.
Consideremos a variável aleatória X - “número de vezes que ocorre o
acontecimento A”. Se a experiência se realizou uma única vez temos:
• em cada prova só há dois resultados possíveis, mutuamente exclusivos,
denominados por sucesso e insucesso;
• a probabilidade de sucesso, designada por p, mantém-se constante de
prova para prova. A probabilidade de insucesso é designada por 1´p “
q;
• as provas são independentes, isto é, os resultados obtidos numa certa
prova ou sequência de provas não afectam os resultados das provas
subsequentes.
Exemplo 3.2. Consideremos o lançamento aleatório de um dado cinco vezes e a ocorrência de um número superior a dois em cada lançamento. O
lançamento é bem sucedido se sair um número superior a dois. Assim, a probabilidade de sucesso é p “ 64 “ 23 . Este é um processo de Bernoulli (sucessão
de provas de Bernoulli), visto que:
• consiste em cinco provas (lançamentos) repetidas;
C. Fernandes & P. Ramos
17/62
0
q
1
p
e
E rXs “ 0 ˆ q ` 1 ˆ p “ p,
“ ‰
V ar rXs “ E X 2 ´ pE rXsq2 “
“ 02 ˆ q ` 12 ˆ p ´ p2 “ p p1 ´ pq “ p ˆ q.
Suponhamos agora que a experiência se realizou n vezes. A variável aleatória X pode tomar os valores 0, 1, 2, . . . , n. Queremos determinar a probabilidade correspondente a cada valor de X. Consideremos o acontecimento
X “ x, ou seja, em x das n provas ocorre A e nas outras n ´ x ocorre A.
Teremos,
A
A ¨¨¨ A A
A ¨¨¨ A.
(1)
looooomooooon
looooomooooon
x vezes
• cada prova (lançamento) tem dois resultados possíveis: sucesso ou insucesso;
Variáveis aleatórias e modelos teóricos unidimensionais
xi
f pxi q
n´x vezes
Como as provas são independentes, a probabilidade correspondente à situação
apresentada em (1) será p ¨ ¨ ¨ pˆq ¨ ¨ ¨ q “ px q n´x . Mas a situação apresentada
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
18/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
em (1) é apenas uma das formas de como pode ocorrer A, x vezes e A, n ´ x
vezes.
O número de maneiras diferentes como isto pode ocorrer é dado por:
Exemplo 3.3. A Sara e Catarina são amigas que gostam muito de jogar
xadrez, mas a Sara é uma grande especialista e ganha 60% dos jogos. Assim,
resolveram efectuar, no próximo fim-de-semana, um campeonato de 15 jogos.
Qual é a probabilidade da Sara ganhar:
n
Cx “
3.3.1
n!
.
x! pn ´ xq!
(a) exactamente 10 jogos?
Consideremos a variável aleatória X - “o número de jogos que a Sara
vence”. Então X „ b pn “ 15; p “ 0, 6q. Assim:
Função de probabilidade
A função de probabilidade é dada por:
" n
Cx px p1 ´ pqn´x , se x “ 0, 1, 2, . . . , n
P rX “ xs “ f pxq “
,
0
, se x ‰ 0, 1, 2, . . . , n
sendo n e p os parâmetros caracterizadores desta distribuição, o parâmetro
n corresponde ao número de provas a realizar e o parâmetro p corresponde à
probabilidade de sucesso.
O nome de distribuição binomial vem do facto de f pxq corresponder aos
termos do desenvolvimento do binómio:
pp ` qqn “ nC0 p0 q n ` nC1 pq n´1 ` nCn pn q 0 .
3.3.2
Função de distribuição ou função cumulativa
‚ V ar rXs “ 15 ˆ 0, 6 ˆ 0, 4 “ 3, 6.
Então P rX “ 10s “ f p10q “ 15C10 ˆ 0, 610 ˆ 0, 415´10 “ 0, 186.
(b) pelo menos 10 jogos?
P rX ě 10s “ 1 ´ P rX ă 10s “ 1 ´ F p9q “ 1 ´
0, 415´j “ 0, 403.
Valor médio, valor esperado ou esperança matemática
E rXs “ n ˆ p.
Se n “ 1 vimos que V ar rXs “ p ˆ q. Para as n repetições da experiência
teremos:
V ar rXs “ n ˆ p ˆ q.
15
Cj ˆ 0, 6j ˆ
Aditividade nas distribuições binomiais
A soma de duas ou mais variáveis aleatórias independentes com distribuição
binomial de parâmetro p, é ainda uma variável aleatória com distribuição
binomial e com o mesmo parâmetro p. Assim, considerando k varáveis aleatórias, Xi , com i “ 1, . . . , k, independentes em que Xi „ b pni , pq, tem-se
˜
¸
k
k
ÿ
ÿ
X “ X1 ` ¨ ¨ ¨ ` Xk “
Xi „ b n “
ni , p .
i“1
C. Fernandes & P. Ramos
j“0
P rX ě 2s “ 1 ´ P rX ă 2s “ 1 ´ P rX “ 0s ´ P rX “ 1s “
“ 1 ´ 4C0 ˆ 0, 990 ˆ 0, 014 ´ 4C1 ˆ 0, 991 ˆ 0, 013 “ 0, 999996.
3.3.5
Variância
Variáveis aleatórias e modelos teóricos unidimensionais
ř9
Exemplo 3.4. Um avião comercial tem 4 motores independentes e num
voo, a probabilidade de cada motor funcionar sem avarias é de 99%. Qual
a probabilidade do avião fazer uma viagem segura se, para isso, precisar de
pelo menos dois motores a funcionar correctamente?
Consideremos a variável aleatória X - “o número de motores a funcionar
sem avarias”. Então X „ b pn “ 4; p “ 0, 99q e
Se n “ 1 vimos que E rXs “ p. Para as n repetições da experiência teremos:
3.3.4
‚ E rXs “ 15 ˆ 0, 6 “ 9;
(c) entre 4 e 8 jogos?
ř
P r4 ď X ď 8s “ 8j“4 15Cj ˆ 0, 6j ˆ 0, 415´j “ 0, 388.
A função distribuição é dada por:
$
0
, se x ă 0
& ř
x
n´j
n
j
P rX ď xs “ F pxq “
, 0ďxďn .
j“0 Cj p p1 ´ pq
%
1
, se x ą n
3.3.3
‚ f pxq “ P rX “ xs “ 15Cx ˆ 0, 6x ˆ 0, 415´x ;
19/62
i“1
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
20/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
3.4
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Distribuição binomial negativa
3.4.3
A distribuição binomial negativa permite descrever o comportamento de uma
variável aleatória que, embora estando associada à repetição de provas de
Bernoulli, envolve um processo de contagem distinto daquele que era descrito
pela distribuição binomial. Denotem-se, respectivamente, por p e q “ 1 ´ p
as probabilidades de sucesso e de insucesso associadas a cada prova de Bernoulli. Numa sequência infinita de provas de Bernoulli, a variável aleatória
X seguirá uma distribuição binomial negativa se representar o número de
provas necessárias até ocorrer o r-ésimo sucesso (r é um número inteiro não
negativo). Em notação simbólica escreve-se X „ BinomialNegativa pr, pq
ou X „ bn pr, pq.
Se somente ao fim de x provas se completarem r sucessos px ě rq, na
x-ésima prova tem de se obter um sucesso, o r-ésimo, e nas x ´ 1 provas
anteriores tem de se obter r ´ 1 sucessos e x ´ r insucessos. Então:
P rX “ xs “ P rr ´ 1 sucessos nas x ´ 1 primeiras provass ˆ
ˆP r1 sucesso na x-ésima provas
3.4.1
Cr´1 pr´1 p1 ´ pqx´1´pr´1q p “
Cr´1 pr p1 ´ pqx´r “
x´1
Cr´1 pr q x´r .
x´1
Função de probabilidade
(a) Determine a probabilidade do segundo candidato aprovado ser o quinto.
Considere-se o sucesso como sendo o acontecimento A - “candidato
passar no exame de condução” cuja probabilidade é p “ 0, 6. Seja X
- “número de candidatos que efectuam o exame até que tenham sido
aprovados r candidatos” e Y - “número de candidatos aprovados em n
exames”. Então X „ bn pr; p “ 0, 6q e Y „ b pn; p “ 0, 6q. Neste caso
temos X „ bn pr “ 2; p “ 0, 6q e pretende-se obter:
e
sendo r e p os parâmetros caracterizadores desta distribuição, o parâmetro r
corresponde ao número de sucessos e o parâmetro p corresponde à probabilidade de sucesso.
Valor médio, valor esperado ou esperança matemática
P r2 ď X ď 4s “ P rX “ 2s ` P rX “ 3s ` P rX “ 4s “
“ 2´1C2´1 p0, 6q2 p0, 4q2´2 ` 3´1C2´1 p0, 6q2 p0, 4q3´2 `
`4´1C2´1 p0, 6q2 p0, 4q4´2 “
“ 0, 821.
No segundo caso temos: Y „ b pn “ 4; p “ 0, 6q e
Se X segue uma distribuição binomial negativa então:
P rY ě 2s “ 1 ´ P rY “ 0s ´ P rY “ 1s “
“ 1 ´ 4C0 p0, 6q0 p0, 4q4 ´ 4C1 p0, 6q p0, 4q3 “
“ 0, 821.
r
E rXs “ .
p
C. Fernandes & P. Ramos
Exemplo 3.5. A probabilidade de um candidato passar no exame de condução é 0, 6.
O acontecimento B - “o segundo candidato a ser aprovado é o segundo,
terceiro ou quarto a realizar o exame” é equivalente ao acontecimento C
- “pelo menos dois dos próximos 4 candidatos são aprovados”. Enquanto
o primeiro acontecimento sugere o recurso à variável aleatória X, o
segundo sugere o recurso à variável Y . Vamos resolver o problema das
duas maneiras e verificar que se obtém o mesmo resultado. No primeiro
caso temos:
X „ bn pr “ 2; p “ 0, 6q
x´1
Variáveis aleatórias e modelos teóricos unidimensionais
r p1 ´ pq
rq
“ 2.
p2
p
(b) Determine a probabilidade de pelo menos dois dos próximos 4 candidatos serem aprovados.
Uma variável aleatória X com função de probabilidade dada por:
" x´1
Cr´1 pr q x´r , x “ r, r ` 1, r ` 2, . . .
f pxq “
,
0
, x ‰ r, r ` 1, r ` 2, . . .
3.4.2
V ar rXs “
P rX “ 5s “ 5´1C2´1 p0, 6q2 p0, 4q5´2 “ 0, 092.
pelo que
P rX “ xs “
“
“
Variância
Se X segue uma distribuição binomial negativa então:
21/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
22/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
3.4.4
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Aditividade na distribuição binomial negativa
3.5.2
Se Xi „ bn pri ; pq, com i “ 1, . . . , n, e X1 , X2 , . . . , Xn são variáveis aleatórias
independentes, então
˜
¸
n
n
ÿ
ÿ
X “ X1 ` ¨ ¨ ¨ ` Xn “
Xi „ bn r “
ri ; p .
i“1
O valor esperado de Y é dado por:
E rY s “ E rXs ´ r “
rq
p
V ar rY s “ V ar rXs “
rq
.
p2
3.5.3
Valor médio, valor esperado ou esperança matemática
Se X segue uma distribuição geométrica então:
1
E rXs “ .
p
3.5.4
Variância
P rX ď k ` c | X ą ks “ P rX ď cs
ou, de forma equivalente,
P rX ą k ` c | X ą ks “ P rX ą cs .
Observação 3.2. Seja X uma variável aleatória com distribuição geométrica
que representa o número de provas realizadas até à obtenção do primeiro sucesso, inclusive. Então, Y “ X ´ 1 representa o número de tentativas falhadas, o número de insucessos, antes do primeiro sucesso, pelo que a função
de probabilidade de Y é dada por:
f pyq “ p p1 ´ pqy ,
y “ 0, 1, 2, . . . .
O valor esperado de Y é dado por:
E rY s “ E rXs ´ 1 “
Função de probabilidade
A função de probabilidade de X é dada por:
"
p p1 ´ pqx´1 , x “ 1, 2, . . .
f pxq “
.
0
, x ‰ 1, 2, . . .
Variáveis aleatórias e modelos teóricos unidimensionais
1´p
q
“ 2.
p2
p
A distribuição geométrica é a única distribuição discreta que não tem
memória, isto é, o número de provas que tem de se realizar, a partir de um
dado momento até se conseguir o primeiro sucesso, não depende do número
de provas já realizadas anteriormente. Assim,
Distribuição geométrica
C. Fernandes & P. Ramos
k“1
p p1 ´ pqk´1 “ 1 ´ p1 ´ pqx .
V ar rXs “
Consideremos a sequência infinita de provas de Bernoulli, isto é, uma espécie
de processo de Bernoulli generalizado para um número infinito de provas.
A distribuição geométrica está relacionada com este processo e representa o
número de provas de Bernoulli realizadas até à obtenção do primeiro sucesso,
com probabilidade p de sucesso em cada prova. Seja X o número de provas de
Bernoulli realizadas até à obtenção do primeiro sucesso, inclusive, com probabilidade p de sucesso em cada prova. Então, X tem distribuição geométrica
com parâmetro p e escreve-se X „ Geométrica ppq ou X „ Geom ppq.
3.5.1
x
ÿ
Se X segue uma distribuição geométrica então:
No caso particular em que r “ 1, X representa o número de provas
de Bernoulli realizadas até à ocorrência, pela primeira vez, de um sucesso,
e a distribuição binomial negativa converte-se naquela que se designa por
distribuição geométrica.
3.5
F pxq “ P rX ď xs “
i“1
Observação 3.1. Seja X o número de provas de Bernoulli realizadas até à
obtenção do r-ésimo sucesso, inclusive, com probabilidade p de sucesso em
cada tentativa. Então, Y “ X ´r representa o número de tentativas falhadas
(insucessos) antes do r-ésimo sucesso, pelo que a função de probabilidade de
Y é dada por:
f pyq “ y`r´1Cy pr q y , y “ 0, 1, 2, . . . .
e a variância por:
Função de distribuição ou função cumulativa
A função de distribuição de probabilidade da variável aleatória X é dada por:
q
1´p
“
p
p
e a variância por:
V ar rY s “ V ar rXs “
23/62
1´p
q
“ 2.
p2
p
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
24/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Exemplo 3.6. Suponha que se contou o número de lançamentos efectuados
de um dado, não viciado, até se conseguir obter “6”.
(a) Determine o valor esperado do número de lançamentos.
Defina-se sucesso como o acontecimento “sair 6” no lançamento do
dado, cuja probabilidade é p “ 61 . Seja X - “número de
` lançamentos
˘
efectuados até sair 6, inclusive”. Então X „ Geom p “ 61 e tem
função de probabilidade dada por:
ˆ ˙ ˆ ˙x´1
1
5
1
f pxq “
, x “ 1, 2, . . . .
6
6
6
Logo temos µ “ E rXs “
1
p
“ 6.
(b) Determine a probabilidade de se efectuarem exactamente 4 lançamentos.
Função de probabilidade
Consideremos
n repetições independentes da experiência E. Se P rAi s “ pi
ř
então ki“1 pi “ 1. Consideremos as variáveis aleatórias X1 , X2 , . . . , Xk sendo
Xi o número de vezes que Ai ocorre nas n repetições da experiência E, com
i “ 1, . . . , n. As variáveis aleatórias Xi são independentes. A probabilidade
de X1 ocorrer x1 vezes,
ř X2 ocorrer x2 vezes, . . . , Xk ocorrer xk vezes, tendo
em conta que n “ ki“1 xi , é dada por:
P rX1 “ x1 , X2 “ x2 , . . . , Xk “ xk s “
Valor médio, valor esperado ou esperança matemática
ˆ ˙ ˆ ˙3
5
1
“ 0, 096.
6
6
E rXi s “ n ˆ pi ,
(c) Determine a probabilidade de se efectuarem mais de 2 lançamentos.
n!
px1 px2 ¨ ¨ ¨ pxk k ,
x1 !x2 ! ¨ ¨ ¨ xk ! 1 2
com xi “ 0, . . . , n e i “ 1, . . . , k.
Podemos escrever pX1 , X2 , . . . , Xk q „ Multinomial pn; p1 ; p2 ; . . . ; pk q ou
pX1 , X2 , . . . , Xk q „ M pn; p1 ; p2 ; . . . ; pk q.
3.6.2
A probabilidade pedida é:
P rX “ 4s “
3.6.1
3.6.3
i “ 1, . . . , k.
Variância
A probabilidade pedida é:
˙2 ff
ˆ
1
“ 0, 694.
P rY ą 2s “ 1 ´ P rY ď 2s “ 1 ´ F p2q “ 1 ´ 1 ´ 1 ´
6
«
(d) Determine a probabilidade de se efectuarem entre 4 e 5 lançamentos,
inclusive.
A probabilidade pedida é:
P r4 ď X ď 5s “ P rX “ 4s`P rX “ 5s “ 0, 096`
3.6
ˆ ˙ ˆ ˙4
1
5
“ 0, 176.
6
6
Distribuição multinomial
C. Fernandes & P. Ramos
i “ 1, . . . , k.
Exemplo 3.7. O tempo, em minutos, gasto por um cliente numa determinada loja, é uma variável aleatória X em que a probabilidade de demorar
menos de 14 minutos é 52 e a probabilidade de demorar entre 14 e 25 minutos
é 31 . Qual é a probabilidade de, em 12 clientes, metade demorarem menos de
14 minutos e quatro demorarem entre 14 e 25 minutos?
Sejam:
• Y1 - “Número de clientes, em 12, que demoraram menos de 14 minutos”;
• Y2 - “Número de clientes, em 12, que demoraram entre 14 e 25 minuto”;
• Y3 - “Número de clientes, em 12, que demoraram mais de 25 minutos”.
É considerada uma generalização da distribuição binomial ao caso em que
em cada repetição de uma experiência, existem mais do que dois resultados
possíveis.
Consideremos uma experiência E com espaço amostral S e k acontecimentos A1 , A2 , . . . , Ak que constituem uma partição de S. Assim, quando a
experiência E se realiza, um e um só dos acontecimentos Ai ocorre.
Variáveis aleatórias e modelos teóricos unidimensionais
V ar rXi s “ n ˆ pi ˆ p1 ´ pi q “ n ˆ pi ˆ qi ,
25/62
As variáveis Y1 , Y2 e Y3 são variáveis aleatórias independentes. Consideremse os acontecimentos mutuamente exclusivos:
• A1 - “Cliente demorar menos de 14 minutos”;
• A2 - “Cliente demorar entre 14 e 25 minutos”;
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
26/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
• A3 - “Cliente demorar mais de 25 minutos”;
como sendo “Sucesso 1”, “Sucesso 2” e “Sucesso 3”, respectivamente, cujas
probabilidades são constantes de cliente para cliente.
Então temos,
pY1 , Y2 , Y3q „ M pn “ 12; p1 ; p2 ; p3 q ,
onde p1 “ P rX ă 14s “ 52 , p2 “ P r14 ď X ď 25s “ 13 e p3 “ P rX ą 25s “
4
, pois A1 , A2 e A3 constituem uma partição de S. A probabilidade pedida
15
é:
ˆ ˙6 ˆ ˙4 ˆ ˙2
2
1
4
12!
“ 0, 0498.
P rY1 “ 6, Y2 “ 4, Y3 “ 2s “
6!4!2! 5
3
15
3.7
Distribuição hipergeométrica
A distribuição hipergeométrica surge, frequentemente, quando se escolhem
elementos de um conjunto finito constituído por dois tipos de objectos. Mais
concretamente, suponha que se tem um número finito de N objectos, dos
quais K são de um tipo e os restantes de outro tipo. Vai escolher-se, sucessivamente, e sem reposição, n dos N objectos pn ď Nq.
Seja X a variável aleatória que representa o número de objectos escolhidos do primeiro tipo. Como se vê, a distribuição hipergeométrica é uma
distribuição discreta que está relacionada com a distribuição binomial. De
facto, pode pensar-se na distribuição hipergeométrica, tal como na binomial,
para representar o número de sucessos numa sequência de n provas, cada
uma com dois resultados possíveis - sucesso ou insucesso. Porém, não havendo reposição, deixará também de se verificar independência e claramente
a probabilidade de sucesso varia de extracção para extracção. Convém
`
˘ no
N
entanto referir que, se n é pequeno, quando comparado com N n ă 10
,a
distribuição binomial com p “ K
pode constituir uma aproximação razoável
N
da distribuição hipergeométrica.
Esta distribuição tem grande utilidade na amostragem estatística (sem
reposição). Os parâmetros N e n são, respectivamente, os tamanhos (finitos)
da população e da amostra. Quanto a K, é o número de elementos do tipo
pretendido existentes na população.
Seja X o número de sucessos contidos numa amostra de tamanho n
retirada, sem reposição, de uma população de N elementos, dos quais K
pK ď Nq constituem sucesso. Então X tem distribuição hipergeométrica
com parâmetros N, n e K e escreve-se X „ Hipergeométrica pN; n; Kq ou
X „ h pN; n; Kq.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
27/62
O número total de amostras será igual ao número de maneiras de seleccionar um subconjunto de n elementos de uma população de tamanho N,
isto é, NCn . Destas, as que possuem x elementos do tipo pretendido serão
em número de KCx ; obviamente, estas amostras possuem os n ´ x restantes
elementos do outro tipo que poderão ser escolhidos de N ´KCn´x maneiras
diferentes. O número de amostras com x elementos do tipo pretendido será
dado por KCx ˆ N ´KCn´x e assim, a probabilidade de se obterem x elementos
do tipo pretendido será:
Cx ˆ N ´KCn´x
.
NC
n
K
P rX “ xs “
3.7.1
Função de probabilidade
f pxq “
3.7.2
KC ˆN´KC
x
n´x
NC
n
0
, se x “ max t0, n ´ N ` Ku , . . . , min tK, nu
.
, outros valores de x
Valor médio, valor esperado ou esperança matemática
com p “
3.7.3
#
E rXs “ n ˆ p,
K
.
N
Variância
N ´n
,
N ´1
´n
. O termo N
é chamado de factor de correcção da população
com p “ K
N
N ´1
finita que resulta de não haver reposição numa população finita de tamanho
N.
V ar rXs “ n ˆ p ˆ p1 ´ pq ˆ
Exemplo 3.8. Seja X o número de alunas numa turma que foram seleccionadas aleatoriamente, para participar nas Olimpíadas de Matemática da
escola. A turma tem 25 alunos, dos quais 10 são rapazes e a equipa participante é constituída por 5 elementos. Determine:
(a) a distribuição de X;
Defina-se sucesso como o acontecimento A - “escolher aluna”. A pro15
porção de alunas existentes na turma é p “ K
“ 25
“ 35 . Seja X N
“número de alunas que fazem parte do grupo de 5 alunos selecciona15
ˆ10C5´x
.
dos”. Então X „ h pN “ 25; n “ 5; K “ 15q, com f pxq “ Cx25
C5
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
28/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
(b) o valor esperado do número de alunas seleccionadas;
E rXs “ 5 ˆ
3
5
Sejam:
“ 3.
• X1 - “Número de navios tanque europeus”;
(c) a probabilidade de se seleccionarem mais de três alunas;
P rX ą 3s “ P rX “ 4s ` P rX “ 5s “
15C ˆ10C
4
1
25C
5
`
15C ˆ10C
5
0
25C
5
• X2 - “Número de navios tanque japoneses”;
“ 0, 313.
(d) Use a aproximação binomial para calcular a probabilidade da alínea
anterior.
`
˘
Aproximação à distribuição binomial: X „b
9 n “ 5; p “ 15
“ 0, 6 .
25
P rX ą 3s “ P rX “ 4s ` P rX “ 5s “ 5C4 ˆ 0, 64 ˆ 0, 41 ` 5C5 ˆ 0, 65 ˆ
N
ˆ0, 40 “ 0, 337. Note-se que a aproximação seria melhor se n ă 10
.
3.8
• X3 - “Número de navios tanque americanos”.
Tendo-se um total de N “ 10 navios, pretendem-se seleccionar n “ 6
navios. Não faz sentido fazer a selecção com reposição. Assim temos a
extracção de 6 navios sem reposição. Temos ainda que: M1 “ 5, M2 “ 3 e
M3 “ 2. A probabilidade pedida é:
5
P rX1 “ 3, X2 “ 2, X3 “ 1s “
Distribuição hipergeométrica generalizada
A distribuição hipergeométrica generalizada representa uma generalização da
distribuição hipergeométrica para a situação em que a população é constituída por k tipos diferentes de elementos (ou objectos).
3.8.1
Função de probabilidade
Suponha uma população com N elementos dos quais M1 são do tipo 1, M2
do tipo 2, . . . , Mk do tipo k. É retirada uma amostra de n elementos sem reposição. Sejam X1 , X2 , . . . , Xk as variáveis aleatórias tais que Xi representa
o número de elementos do tipo i na amostra, com i “ 1, . . . , k. A probabilidade de se obterem m1 elementos do tipo 1, m2 do tipo 2, . . ., mk do tipo k
é dada por:
M1
P rX1 “ m1 , X2 “ m2 , . . . , Xk “ mk s “
onde mi “ 0, 1, 2, . . . , n,
řk
i“1
mi “ n e
řk
i“1
Cm1 ˆ M2Cm2 . . . ˆ MkCmk
,
NC
n
Mi “ N.
Exemplo 3.9. Como resultado da crise do Golfo, a produção de petróleo de
um dos países da OPEP apresentou quebras da ordem dos 30%, o que não
lhe permitiu satisfazer integralmente os compromissos anteriormente assumidos: o abastecimento de cinco navios tanque europeus, três japoneses e dois
americanos. Sabendo que 70% da sua produção lhe permite abastecer apenas
seis dos navios tanque, decidiu seleccionar aleatoriamente os navios tanque
a abastecer. Qual a probabilidade de serem seleccionados três navios tanque
europeus, dois japoneses e apenas um americano?
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
29/62
3.9
C3 ˆ 3C2 ˆ 2C1
“ 0, 286.
10C
6
Distribuição de Poisson
A distribuição binomial usa-se em situações, em que, além de conhecermos o
tamanho da amostra, sabemos quantas vezes é que um acontecimento ocorreu e quantas não ocorreu. Ora, nem sempre isso é possível. Quando ocorre
uma tempestade e resolvemos observar o céu durante uma hora, para contar
o número de relâmpagos, não faz sentido falarmos do número de vezes que
não relampejou. Outros exemplos são a contagem dos golos num desafio de
futebol, o número de erros ortográficos num livro e o número de defeitos numa
toalha de renda. Em qualquer destas situações, estamos interessados no número de acontecimentos que ocorrem durante um dado intervalo temporal ou
numa dada região espacial. Recorremos, nestes casos, à distribuição de Poisson, que tem na sua génese um processo de Poisson, tal como a distribuição
binomial tem o processo de Bernoulli.
Um processo de Poisson refere-se, normalmente, ao número de ocorrências de um acontecimento num intervalo temporal ou numa região espacial
(tempo, comprimento, área ou volume). Tem as seguintes propriedades:
• não tem memória (o número de ocorrências de um acontecimento num
intervalo é independente do número de ocorrências noutro intervalo
disjunto);
• a probabilidade de ocorrência de um acontecimento é a mesma para
intervalos com a mesma amplitude;
• a probabilidade de ocorrer mais do que um acontecimento, num intervalo suficientemente pequeno, é nula.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
30/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Seja λ ą 0 o número médio de ocorrências de um acontecimento num dado
intervalo de tempo ou numa dada região espacial (espaço contínuo temporal
ou espacial) e seja X uma variável aleatória que representa o número de
ocorrências de um acontecimento nesse intervalo de tempo ou nessa região.
X tem distribuição de Poisson com parâmetro λ e escreve-se X „ P oisson pλq
ou X „ P pλq.
3.9.1
3.9.2
"
λx e´λ
x!
0
, se x “ 0, 1, . . .
.
, se x ‰ 0, 1, . . .
3.9.4
Variância
V ar rXs “ λ.
Frequentemente estamos interessados em calcular probabilidades para diversos intervalos de tempo ou espaço, pelo que se torna mais conveniente
definir λ como sendo o número médio de ocorrências de um acontecimento
por unidade de tempo ou espaço. Neste caso, o parâmetro da distribuição
deixará de ser λ e passará a ser λt, em que t é a amplitude do intervalo e
escreve-se X „ P pλtq. Assim, a função de probabilidade é:
f pxq “
Aproximação da distribuição binomial à Poisson
Exemplo 3.11. Uma companhia de seguros possui 10000 apólices no ramo
vida referente a acidentes de trabalho. Sabe-se que, por ano, a probabilidade
de determinado indivíduo morrer de acidente de trabalho é 0,0001. Qual a
probabilidade de a companhia ter de pagar por ano a pelo menos 4 dos seus
segurados?
Consideremos a variável aleatória X - “número de apólices, em 10000, que
são pagas anualmente pela seguradora”. Tem-se X „ b pn “ 10000; p “ 0, 0001q.
Como n “ 10000 e p “ 0, 0001 existem condições para fazer a aproximação à
distribuição de Poisson. Temos então, X „P
9 pλ “ n ˆ p “ 1q. Assim temos,
Valor médio, valor esperado ou esperança matemática
E rXs “ λ.
3.9.3
Seja X2 - “número de partículas α emitidas em 2 milissegundos”, então
λ “ 2 ˆ 2 “ 4. Logo X2 „ P pλ “ 4q e tem-se P rX2 ě 3s “ 1 ´
0 ´4
1 ´4
2 ´4
P rX2 “ 0s´P rX2 “ 1s´P rX2 “ 2s “ 1´ 4 0!e ´ 4 1!e ´ 4 2!e “ 0, 762.
A distribuição binomial converge para a distribuição de Poisson, quando
n Ñ `8 e p Ñ 0, mantendo-se λ “ np constante. A aproximação será tanto
melhor quanto maior for n e menor for p. No entanto a aproximação já é
satisfatória desde que n ą 20 e np ă 5.
Função de probabilidade
f pxq “
(b) serem emitidas pelo menos três partículas em dois milissegundos.
pλtqx e´λt
,
x!
P rX ě 4s “ 1 ´ P rX ă 4s “ 1 ´
10 e´1 11 e´1 12 e´1 13 e´1
`
`
`
0!
1!
2!
3!
“ 1 ´ 0, 981 “ 0, 019.
“ 1´
3.9.5
com x “ 0, 1, . . . , n, . . ., sendo E rXs “ λt e V ar rXs “ λt.
Exemplo 3.10. Um material radioactivo emite partículas α a uma taxa de
duas por milissegundo. Determine a probabilidade de:
3
ÿ
1x e´1
“
x!
x“0
ˆ
˙
“
Aditividade nas distribuições de Poisson
Se X1 , . . . , Xn são variáveis aleatórias independentes, com Xi „ P pλi q, para
i “ 1, . . . , n, então
˜
¸
n
n
ÿ
ÿ
Xi „ P
λi .
i“1
i“1
(a) serem emitidas duas partículas num milissegundo;
Seja Xt - “número de partículas α emitidas em t milissegundos”. Então,
x ´2
X1 „ P pλ “ 2 ˆ 1q e f pxq “ 2 x!e , com x “ 0, 1, . . . , n, . . .. Assim,
22 e´2
P rX1 “ 2s “ f p2q “ 2! “ 0, 271.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
31/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
32/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
4
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Variáveis aleatórias unidimensionais contínuas
y
y= f (x )
Quando a variável aleatória é contínua, o conjunto de possibilidades para X
é infinito.
P [aXb]
Exemplo 4.1. Considerem-se as seguintes variáveis aleatórias:
• X - radiação solar total por dia;
0
• Y - medida das peças produzidas por uma máquina em relação à norma
especificada pela CE;
• Z - Tempo que um robot industrial opera durante uma semana;
Função de densidade de probabilidade
Seja X uma variável aleatória contínua. A função densidade de probabilidade
de X é uma função f pxq tal que:
żb
P ra ď X ď bs “
f pxq dx, @a, b P R : a ď b
a
e que tem as seguintes propriedades:
• f pxq ě 0, @x P R;
ş `8
• ´8 f pxq dx “ 1.
4.2
Função de distribuição
Seja X uma variável aleatória contínua com função densidade de probabilidade f pxq. A função de distribuição de X é dada por:
żx
F pxq “ P rX ď xs “
f psq ds.
´8
Constitui uma consequência da descrição probabilística de X, que para
qualquer valor especificado de X, digamos x0 , teremos
P rX “ x0 s “ 0,
porque
P rX “ x0 s “
ż x0
x0
Esta função tem domínio R, conjunto chegada r0, 1s, e satisfaz as seguintes
propriedades:
• F px2 q ě F px1 q, @x1 , x2 , com x2 ą x1 ;
• limxÑ´8 F pxq “ 0 e limxÑ`8 F pxq “ 1;
• é uma função contínua.
f pxq dx “ 0.
Com x1 ă x2 , podemos calcular a probabilidade de X tomar qualquer valor
no intervalo rx1 , x2 s, por:
P rx1 ď X ď x2 s “ P rx1 ď X ă x2 s “
“ P rx1 ă X ď x2 s “
“ P rx1 ă X ă x2 s “
ż x2
f pxq dx.
“
Observe-se que:
P rx1 ď X ď x2 s “
“
“
“
P rx1 ď X ă x2 s “
P rx1 ă X ď x2 s “
P rx1 ă X ă x2 s “
F px q ´ F px1 q “
ż x2 2
“
f pxq dx.
x1
x1
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
x
b
Exemplo 4.2. São exemplos, os tempos de vida duma componente electrónica de um certo equipamento ou de uma máquina de lavar, em milhares
de horas. Estas variáveis estão definidas em toda a semi-recta positiva da
recta real. Este tipo de variáveis que assumem qualquer valor num intervalo
dizem-se contínuas.
• W - altura das crianças, em metros.
4.1
a
33/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
34/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
• Para 0 ă x ď 4:
y
ż0
y= F(x )
1
´8
• Para x ą 4:
x
0
y
y
y= f (x )
0
F (b)=P [Xb]
x
a
y
´8
y= f (x )
F (a)=P [Xa]
b
0
x
b
żx
´8
x
0 ds “ 0;
Variáveis aleatórias e modelos teóricos unidimensionais
0
1
1
s ds “ x2 ;
8
16
1
s ds `
8
żx
4
0 ds “ 1.
De uma forma genérica podemos dizer que a função densidade de probabilidade pode ser obtida por derivação da função distribuição. Do teorema
fundamental do cálculo sabemos que
ż
d x
f psq ds “ f pxq .
dx ´8
dF pxq
dx
desde que a derivada exista.
Seja f , a função densidade, e F , a função distribuição de uma variável
aleatória contínua X. Se f é seccionalmente contínua em R (isto é, contínua
em R, com excepção de um número finito ou de uma infinidade numerável de
pontos de descontinuidade de 1a espécie), então F é derivável em qualquer
ponto de continuidade, x, de f e, nesse ponto, F 1 pxq “ f pxq.
Para obter a função de distribuição teremos que considerar os seguintes
casos:
C. Fernandes & P. Ramos
0
f pxq “
Exemplo 4.3. Considere a variável aleatória X com função densidade de
probabilidade
" 1
x , 0ăxď4
.
f pxq “ 8
0 , fora do intervalo
• Para x ď 0:
ż4
Então, dada F pxq
y= f (x )
a
0 ds `
żx
A função de distribuição desta variável será:
$
, xď0
& 0
1 2
F pxq “
x , 0ăxď4 .
16
%
1
, xą4
F (b)−F (a)=P [aXb]
0
ż0
0 ds `
35/62
Observação 4.1.
• Atendendo a que o número de descontinuidades é numerável, elas são
descontinuidades isoladas, isto é, existe uma vizinhança desse ponto
onde ela é a única descontinuidade.
• As funções densidade que consideramos são limitadas em R, isto é, os
possíveis pontos de descontinuidade são descontinuidades de 1a espécie.
Recordemos que um ponto de descontinuidade é de 1a espécie quando os
limites laterais da função nesse ponto existem, são diferentes e finitos,
enquanto que um ponto de descontinuidade é de 2a espécie quando, pelo
menos, um dos limites laterais no ponto é 8, isto é, a esse ponto está
associado uma assimptota vertical ao gráfico da função.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
36/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
• Quando a função densidade f é contínua num ponto x P R (e supomos
que pode existir um número finito de pontos, ou uma infinidade numerável de pontos de descontinuidade de f ), existe F 1 pxq e F 1 pxq “ f pxq.
Num ponto de descontinuidade de 1a espécie de f , admitimos que f assume um valor real que permite determinar de forma única, F pxq, embora não exista F 1 pxq. Assim, a uma função distribuição, podem estar
associadas uma infinidade de funções densidade, todas elas diferentes
entre si, apenas em um número finito ou uma infinidade numerável de
pontos.
No exemplo que se segue, é conhecida a função distribuição de uma variável aleatória contínua, logo uma função contínua em R e pretendemos
construir uma função densidade que lhe esteja associada.
• se x “ 3,
Fd1 p3q “ lim`
xÑ3
e
F pxq “
0
1 3
x
27
%
1
lim´
xÑ3
ou seja, não existe F 1 p3q.
Então,
F 1 pxq “
com o gráfico:
, se x ă 0
, se 0 ď x ď 3
, se x ą 3
"
-5
1
0,5
-4
-3
-2
-1
1
2
3
4
5
x
Estudemos a derivada desta função nos pontos do seu domínio:
• se x ă 0 ou x ą 3, F 1 pxq “ 0;
Fd1 p0q “ lim`
xÑ0
logo F p0q “ 0;
-2
-1
0
1
2
3
4
5
x
A função F pxq, como verificamos, não tem derivada no ponto x “ 3. De
forma a obter uma função f pxq, que seja função densidade de probabilidade
de uma variável aleatória contínua e que tenha F pxq como sua função distribuição, atribuiremos um valor a f p3q. Se definirmos f p3q “ 1, obteremos
a função
" 1 2
x , se x P r0, 3s
,
f pxq “ 9
0 , se x ‰ r0, 3s
´0
“0
x´0
1
0´0
“ 0,
x´0
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
-3
f (x)
Fe1 p0q “ lim´
1
-4
1 3
x
27
xÑ0
e
, se x P r0, 3r
, se x R r0, 3s
cujo gráfico é:
• se 0 ă x ă 3, F 1 pxq “ 91 x2 ;
• se x “ 0,
0
1
F (x)
-5
1 2
x
9
F'(x)
a função distribuição de uma variável aleatória X, cujo gráfico é:
0
1 3
x
27
´1
“
x´3 `
˘
1 2
px ´ 3q 27
x ` 19 x ` 13
“ lim´
“ 1,
xÑ3
x´3
Fe1 p3q “
Exemplo 4.4. Seja
$
&
1´1
“0
x´3
-5
37/62
-4
-3
-2
-1
0
1
2
3
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
4
5
x
38/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Facilmente, se verifica que
ż `8
´8
f pxq dx “
• quanto à dispersão - variância, desvio padrão e desvio médio;
ż3
0
2
„
3
x
x
dx “
9
27
ȷ3
0
• quanto à assimetria - parâmetro γ1 ;
“ 1,
• quanto ao achatamento ou curtose - parâmetro β3 .
com f pxq ě 0, @x P R e que
F pxq “ P rX ď xs ,
4.4
@x P R.
Podemos definir os seguintes momentos:
Observe-se que atribuindo, por exemplo, f p3q “ 0, em vez de f p3q “ 1,
também se teria solucionado o problema.
Nota e Complemento 4.1. (ver Murteira, B. e Ribeiro, C.S. (2010). Introdução à Estatística. Escolar Editora). Nos pontos
x P R, em que existe
şx
F 1 pxq, tem-se que F 1 pxq “ f pxq, pois F pxq “ ´8 f psq ds. Assim, convencionando escrever f pxq “ 0 nos pontos em que F 1 pxq não existe, conclui-se
que a função densidade de probabilidade determina univocamente a função
de distribuição. Se a função de distribuição é absolutamente contínua, como
presentemente se está a admitir, F 1 pxq existe quase por toda a parte, isto é,
existe excepto quando muito para um conjunto de pontos de R com medida à
Lebesgue igual a zero. Assim, as funções densidade compatíveis com a função
de distribuição F pxq só diferem em conjuntos com medida nula. Isto é, a
função f pxq determinada com a convenção referida (f pxq “ 0 nos pontos
em que F 1 pxq não existe) e todas as funções densidade f0 pxq, quase iguais
a f pxq (f0 pxq “ f pxq excepto em pontos x em que não existe F 1 pxq e que
formam um conjunto com medida nula) representam a infinidade de versões
de funções densidade compatíveis com a mesma função de distribuição F pxq.
Ao adoptar a referida convenção opta-se por uma das versões sabendo, aliás,
que as conclusões da análise probabilística não são afectadas. O que conta de
facto é a função de distribuição.
4.3
Parâmetros das variáveis aleatórias unidimensionais
continuas
Quando temos os valores que uma variável aleatória pode tomar e a respectiva
função de densidade de probabilidade, temos definida uma distribuição de
probabilidade. Uma distribuição de probabilidade estuda-se através de:
• parâmetros, momentos ou parâmetros de ordem;
• relativamente à localização ou tendência central - valor médio, moda e
mediana;
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
Momentos
39/62
“ ‰
• momentos de ordem k em relação à origem, E X k , com k inteiro
positivo:
ż `8
“ ‰
E Xk “
xk f pxq dx;
´8
• momentos
de ordem
k em relação à média ou momento central de ordem
”
ı
k, E pX ´ µqk , com k inteiro positivo:
ı ż `8
”
E pX ´ µqk “
px ´ µqk f pxq dx.
´8
4.5
Valor médio, valor esperado ou esperança matemática
É o primeiro momento em relação à origem,
E rXs “ µ.
O valor médio indica o ponto em torno do qual mais se concentra a densidade
de probabilidade. Define-se do seguinte modo:
ż `8
E rXs “
xf pxq dx.
´8
As propriedades do valor médio, que vimos para o caso discreto, mantêmse no caso contínuo.
Exemplo 4.5. Para a variável aleatória do exemplo 4.3, obtemos o valor
médio:
ż `8
ż4
ż4
1
1 2
E rXs “
xf pxq dx “
x ˆ ˆ x dx “
x dx “ 2, 667.
8
´8
0
0 8
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
40/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
4.6
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Os quartis são obtidos considerando:
Mediana
É um parâmetro de ordem que serve para localizar a distribuição ao centro.
Sendo a distribuição contínua, a mediana será o valor de x “ Me que satisfaz:
ż Me
1
F pMeq “
f psq ds “ .
2
´8
Exemplo 4.6. Seja X a variável que descreve o tempo, em minutos, entre
passagens consecutivas na via verde da Ponte Vasco da Gama, no sentido
S-N. A função densidade de probabilidade associada a esta variável é dada
por f pxq “ 0, 1e´0,1x , em que x ě 0. Qual é a mediana de X?
A mediana é o valor Me tal que:
ż Me
ln p0, 5q
F pMeq “ 0, 5 ô
0, 1e´0,1x dx “ 0, 5 ô Me “ ´
ô Me » 6, 93.
0, 1
0
4.7
Quantis
Seja X uma variável aleatória contínua, com função de distribuição F pxq e
p P r0, 1s. Chama-se quantil de probabilidade p ou quantil de ordem p da
variável aleatória X, ao valor χp tal que
F pχp q “ p.
F pχ0,25 q “ 0, 25;
• 2o quartil ou mediana:
F pχ0,5 q “ 0, 5;
• 3o quartil:
F pχ0,75 q “ 0, 75.
Exemplo 4.7. Para a variável aleatória do exemplo 4.6, determine os quartis
da variável aleatória de X?
A função densidade de probabilidade é dada por:
, x ě 0.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
ż χ0,25
0, 1e´0,1x dx “ 0, 25 ô χ0,25 » 2, 88;
ż χ0,5
0, 1e´0,1x dx “ 0, 5 ô χ0,5 » 6, 93;
0
• 2o quartil ou mediana:
F pχ0,5 q “ 0, 5 ô
0
• 3o quartil:
F pχ0,75 q “ 0, 75 ô
ż χ0,75
0
0, 1e´0,1x dx “ 0, 75 ô χ0,75 » 13, 86.
Assim podemos dizer que cerca de 25% dos valores da distribuição de probabilidade do tempo, em minutos, entre passagens consecutivas na via verde
da Ponte Vasco da Gama, no sentido S-N, são inferiores a 2, 88 minutos e
que cerca de 75% são inferiores a 13, 86 minutos. Podemos ainda referir que
cerca de 75% dos valores da distribuição de probabilidade do tempo, em minutos, entre passagens consecutivas na via verde da Ponte Vasco da Gama,
no sentido S-N, são superiores ou iguais a 2, 88 minutos e que cerca de 25%
são superiores ou iguais a 13, 86 minutos.
Moda
É um parâmetro de ordem que é o valor ou valores de x, pois a distribuição
pode ter mais de uma moda, para os quais a função densidade de probabilidade é máxima.
Para uma distribuição contínua, encontram-se os máximos de f pxq determinando a 1a derivada, que se iguala a zero, e avalia-se o sinal da 2a derivada
para ver se efectivamente existe um máximo.
• 1o quartil:
f pxq “ 0, 1e
F pχ0,25 q “ 0, 25 ô
4.8
Os quartis podem ser obtidos considerando:
´0,1x
• 1o quartil:
41/62
Exemplo 4.8. Para a variável aleatória do exemplo 4.6, qual é a moda de
X?
A moda é o valor de x que faz corresponder a f pxq um máximo. Como a
primeira derivada de f pxq é sempre negativa, tendendo para zero à medida
que x tende para `8,
df
“ ´0, 01e´0,1x ă 0,
dx
a função é decrescente. O valor máximo que a função assume corresponde
ao valor de f pxq quando x “ 0 (valor mínimo do domínio da função), ou
seja, f p0q “ 0, 1, pelo que Mod “ 0 minutos.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
42/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
4.9
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Variância
4.11
O 2o momento em relação à média ou 2o momento central,
“
‰
E pX ´ µq2 “ V ar rXs “ σ 2 ,
é chamado de variância de X. Como a variância é uma quantidade de 2a
ordem, exprime-se em punidades de Xq2 . Seja X uma variável aleatória, a
2
variância de X representada por V ar rXs “ σX
“ σ 2 define-se por:
ż `8
“
‰
V ar rXs “ E pX ´ µq2 “
px ´ µq2 f pxq dx.
´8
As propriedades da variância, que vimos para o caso discreto, mantêm-se
no caso contínuo.
“
‰
Observação 4.2. Observe-se que V ar rXs “ E pX ´ µq2 “ E rX 2 s´2µ2 `
2
2
2
µ “ E rX s ´ E rXs , com
“
E X
‰
2
“
`8
ż
´8
x2 f pxq dx.
Exemplo 4.9. Para a variável aleatória do exemplo 4.3, temos que:
ż `8
ż4
ż4
“ ‰
1
1 3
E X2 “
x2 f pxq dx “
x2 xdx “
x dx “ 8,
8
´8
0
0 8
É uma medida de dispersão que não depende das unidades em que X foi
medida, tal como vimos no caso discreto, pelo que deve ser usado para comparar variáveis quanto à dispersão, quando estas têm unidades de medida
diferentes ou quando têm valores médios muito diferentes.
4.12
Desvio médio
Nas distribuições contínuas temos:
Dm “ E r|X ´ µ|s “
ż `8
´8
|x ´ µ| f pxq dx.
Exemplo 4.10. Consideremos uma variável aleatória X definida pela seguinte função densidade de probabilidade:
" 3 2
x , se 0 ă x ă 2
.
f pxq “ 8
0 , se x está fora do intervalo
Calcule o desvio médio.
Sendo
E rXs “
obtendo-se a variância
ż2
0
xf pxq dx “
ż2
0
xˆ
3
3
ˆ x2 dx “ ,
8
2
tem-se
V ar rXs “ 8 ´ 2, 6672 “ 0, 887.
4.10
Coeficiente de variação
O coeficiente de variação calcula-se da mesma forma que vimos no caso discreto:
σ
Cv “ ˆ 100%.
µ
ż `8
ż2⏐
⏐
⏐x ´
⏐
⏐
3⏐
⏐ 3 x2 dx “
2⏐ 8
´8
0
˙
˙
ż2ˆ
ż3ˆ
2
3 3 2
3
3 2
x´
´x
x dx `
x dx “ 0, 32.
“
3
2
8
2 8
0
2
Dm “
Desvio padrão
O desvio padrão é a raiz quadrada da variância,
a
σ “ V ar rXs
e exprime-se em unidades de X. Tal como no caso discreto a variância e o
desvio padrão só assumem valores não negativos. Quanto menor for o valor
do desvio padrão maior é a concentração dos valores da variável em torno da
média.
4.13
|x ´ µ| f pxq dx “
Assimetria
A assimetria estuda-se da mesma forma que vimos para o caso discreto.
4.14
Achatamento ou curtose
A curtose estuda-se da mesma forma que vimos para o caso discreto.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
43/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
44/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
5
5.1
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Modelos teóricos unidimensionais contínuos
f ptq “
Distribuição exponencial
A distribuição exponencial é uma das distribuições contínuas mais importantes e é muito usada no estudo de filas de espera e de fiabilidade de sistemas
complexos (fiabilidade no instante t é a probabilidade do sistema ainda funcionar nesse instante).
A distribuição exponencial aparece frequentemente associada a um processo de Poisson, que é um processo que não tem memória e que se refere à
ocorrência de acontecimentos num intervalo de tempo ou numa região espacial. Enquanto a distribuição de Poisson serve como modelo probabilístico
de contagem do número de vezes que ocorre um acontecimento, a distribuição exponencial usa-se para representar o intervalo de tempo entre duas
ocorrências independentes ou o intervalo de tempo até à primeira ocorrência.
De facto, demonstra-se que, num processo de Poisson, o “tempo” de espera
até ao primeiro sucesso ou “tempo” de espera entre dois sucessos consecutivos,
segue uma certa distribuição exponencial. Por exemplo, o tempo entre a
chegada de clientes a um estabelecimento ou o tempo entre a chegada de
encomendas a um armazém ou o tempo entre a ocorrência de avarias ou a
duração (tempo de vida) de máquinas e de outros dispositivos.
Consideremos a variável aleatória X - “número de ocorrências de um
acontecimento por unidade de tempo ou espaço”, com X „ P pλq. Defina-se,
também, uma outra variável T - “tempo de espera até à primeira ocorrência
de um acontecimento”. Esperar pelo menos t tempo até à primeira ocorrência,
é assumir que no intervalo r0, ts não há ocorrências. Seja Xt - “número de
ocorrências no intervalo r0, ts”, então:
P rT ą ts “ P rXt “ 0s “
pλtq0 e´λt
“ e´λt ,
0!
e F ptq “ P rT ď ts “ 1 ´ P rT ą ts “ 1 ´ e´λt , sendo λ o número médio
de ocorrências do acontecimento por unidade de tempo ou espaço. Então a
função de distribuição da variável aleatória T é FT ptq “ P rT ď ts “ 1´e´λt ,
t ě 0. Derivando FT ptq em ordem a t, obtém-se a função densidade de
probabilidade da variável aleatória T , fT ptq “ λe´λt .
5.1.1
dade é dada por:
Função densidade de probabilidade
Se uma variável aleatória contínua T tem distribuição exponencial, escreve-se
T „ Exponencial pλq ou T „ exp pλq e a sua função densidade de probabiliVariáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
45/62
"
λ e´λt , se t ą 0
,
0
, se t ď 0
onde λ é o parâmetro caracterizador da distribuição, sendo λ ą 0.
5.1.2
Função distribuição ou função cumulativa
Sendo T „ exp pλq, a sua função distribuição é dada por:
F ptq “ 1 ´ e´λt ,
5.1.3
Valor médio, valor esperado ou esperança matemática
E rT s “
5.1.4
t ą 0.
1
.
λ
Variância
1
.
λ2
O modelo exponencial aplica-se frequentemente quando se pretende estudar tempos até à ocorrência de falhas, por exemplo em componentes electrónicos, em que se admite que o tempo que a componente vai durar, é
independente do tempo que esta já durou. Isto significa que um componente
com tempo de vida exponencial, tem a mesma qualidade ao longo do tempo,
ou seja, verifica-se a propriedade:
V ar rT s “
P rX ě a ` b | X ě as “ P rX ě bs .
Exemplo 5.1. Os relâmpagos que rasgam o céu durante uma forte tempestade, num determinado local, são estatisticamente independentes e o seu
número tem uma distribuição de Poisson com média de 12 por minuto. Considere a variável aleatória T que representa o intervalo de tempo, em minutos,
entre relâmpagos consecutivos.
(a) Identifique e caracterize a distribuição de T ;
Consideremos as variáveis aleatórias X - “número de relâmpagos por
minuto” com X „ P pλ “ 12q e T - “intervalo de tempo, em minutos,
entre relâmpagos consecutivos”.
Como num processo de Poisson, o tempo de espera entre dois sucessos consecutivos, segue uma distribuição exponencial, temos que T „
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
46/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
exp pλ “ 12q sendo λ “ 12 o número médio de relâmpagos por minuto.
A função distribuição da variável T é dada por F ptq “ 1 ´ e´12t , t ě 0,
1
1
o valor médio por E rT s “ 12
e a variância por V ar rT s “ 144
.
5.2.2
Em alternativa podemos pensar da seguinte forma, não relampejar num
intervalo de 10 segundos é admitir que o intervalo entre dois relâmpagos consecutivos é superior a 10 segundos, logo P rT ą 10s “ 1 ´
P rT ď 10s “ 1 ´ F p10q “ e´2 “ 0, 135.
5.2.3
Logo P rY ě 5s “ P rY “ 5s` P rY “ 6s “ 6C5 ˆ 0, 8655 ˆ 0, 135 ` 6C6 ˆ
0, 8656 ˆ 0, 1350 “ 0, 811.
5.2
5.2.4
5.2.1
V ar rXs “
f pxq “ f px; a; bq “
"
1
b´a
0
, se a ă x ă b
.
, fora do intervalo
Os parâmetros caracterizadores desta distribuição são a e b, que satisfazem
a condição, ´8 ă a ă b ă `8.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
47/62
1
żb
x
a
b`a
1
dx “
.
b´a
2
żb
a
px ´ µq2
1
pb ´ aq2
dx “
.
b´a
12
Exemplo 5.2. Considere o processo de seleccionar números reais, ao acaso,
no intervalo ra, bs. Suponha que selecciona um número no intervalo r5, 7s.
Determine a probabilidade do número estar compreendido entre 6, 3 e 6, 95.
Seja X - “número seleccionado no intervalo r5, 7s”, com X „ U p5; 7q e
f pxq “ 21 , se x P r5, 7s. Tem-se:
E rXs “
7`5
“ 6,
2
e
F pxq “
V ar rXs “
$
& 0
x´5
2
%
1
p7 ´ 5q2
1
“
12
3
, se x ă 5
, se 5 ď x ď 7 .
, se x ą 7
A probabilidade do número seleccionado estar compreendido entre 6, 30 e 6, 95
é dada por: P r6, 3 ď X ď 6, 95s “ F p6, 95q ´ F p6, 3q “ 0, 325.
5.3
Função de densidade de probabilidade
%
, se x ď a
, se a ă x ă b .
, se x ě b
Variância
Distribuição uniforme
Esta distribuição utiliza-se quando os valores de certa variável aleatória podem ocorrer dentro dum intervalo limitado (aberto ou fechado) pa, bq e quaisquer dois subintervalos com a mesma amplitude têm a mesma probabilidade,
ou seja, é usada para representar uma quantidade que varia aleatoriamente
no intervalo pa, bq e cuja probabilidade de tomar valores num subintervalo
de pa, bq é proporcional ao seu comprimento. Se a variável aleatória X tem
distribuição uniforme no intervalo pa, bq escreve-se X „ Unif orme pa; bq ou
X „ U pa; bq.
x´a
b´a
Valor médio, valor esperado ou esperança matemática
E rXs “
(c) Considere intervalos de tempo de 10 segundos. Qual é a probabilidade
de relampejar em pelo menos 5 de 6 intervalos consecutivos?
Seja a variável aleatória Y - “número de intervalos, em 6, em que
relampejou” em que Y „ b pn “ 6; p “ 0, 865q onde p “ P rX 1 ě 1s “
1 ´ P rX 1 “ 0s “ 1 ´ 0, 135 “ 0, 865.
$
& 0
F pxq “ P rX ď xs “
(b) Qual é a probabilidade de não relampejar num intervalo de 10 segundos;
Seja a variável aleatória
X 1 - “número
`
˘ de relâmpagos por 10 segundos”,
12
em que X 1 „ P λ “ 60
ˆ 10 “ 2 pois λ “ 12
o número médio de
60
0 ´2
relâmpagos por segundo. Logo P rX 1 “ 0s “ f p0q “ 2 0!e “ 0, 135.
Função de distribuição
Distribuição normal
A distribuição normal é uma distribuição contínua com a forma de sino e é,
sem qualquer dúvida, a mais importante. Foi De Moivre, no século XVIII,
que determinou a expressão matemática da sua função densidade de probabilidade, calculando o limite da função de probabilidade binomial para um
número infinito de tentativas. Também Gauss (séculos XVIII - XIX) teve
um papel decisivo no seu desenvolvimento e a distribuição normal é também
chamada, em sua honra, distribuição de Gauss.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
48/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
As razões da importância da distribuição normal são várias, mas não se
pode deixar de referir as seguintes:
y
• é um modelo adequado para representar muitos dos fenómenos do
mundo real, nomeadamente, características humanas como a altura e
o peso, e outras características que tenham a ver com medições;
1
σ 2π
• é muito usada na inferência estatística. Tal deve-se, em grande parte
ao facto de, mesmo quando a distribuição não é normal, a distribuição
das médias amostrais ser aproximadamente normal (teorema do limite
central);
• muitas técnicas desenvolvidas em Estatística são exactas no caso de
distribuições normais;
x
0
µ
Quanto maior for o desvio padrão σ, mais achatada é a curva da normal:
• algumas variáveis aleatórias (como, por exemplo, a binomial e a de
Poisson) podem ser aproximadas por uma variável aleatória normal.
5.3.1
Função densidade de probabilidade
σ2
Consideremos uma variável aleatória X que segue uma distribuição normal
com média µ e desvio padrão σ, escrevendo-se X „ Normal pµ; σq ou X „
N pµ; σq. A sua função de densidade de probabilidade é dada por:
1 x´µ 2
1
f pxq “ f px; µ; σq “ ?
e´ 2 p σ q ,
σ 2π
com ´8 ă x ă `8, ´8 ă µ ă `8 e σ ą 0.
5.3.2
σ1
σ2 >σ1
A concavidade da curva muda de sentido em x1 “ µ ´ σ e x2 “ µ ` σ,
sendo x1 e x2 as abcissas dos pontos de inflexão da curva da normal:
Valor médio, valor esperado ou esperança matemática
E rXs “ µ.
5.3.3
µ−σ
Variância
µ
µ+σ
A área abaixo da curva distribui-se em intervalos da seguinte forma:
V ar rXs “ σ 2 .
A distribuição normal é caracterizada pelos valores assumidos pelos parâmetros. Assim conforme o centro da distribuição (média) e a variabilidade
relativamente ao centro (desvio padrão), assim a distribuição apresenta diferente comportamento, bem como diferente aspecto gráfico, mais ou menos
achatada e mais ou menos enviesada. A curva que representa f pxq tem a
forma de um sino e é simétrica em relação à recta x “ µ e a ordenada máxima
da curva corresponde ao ponto µ e é igual a σ?12π :
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
49/62
68,27%
µ−σ
µ
µ+σ
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
50/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
5.3.6
Variância
95,45%
µ−2σ
V ar rZs “ V ar
µ+2σ
µ
„
ȷ
X ´µ
1
“ 2 V ar rX ´ µs “
σ
σ
1
pV ar rXs ` V ar rµsq “
σ2
˘
1 ` 2
σ `0 “
“
σ2
“ 1.
“
99,73%
µ−3σ
µ+3σ
µ
Conclui-se então que Z „ N p0; 1q.
5.3.7
5.3.4
Cálculo de probabilidades na distribuição normal
Uma vez que os parâmetros da distribuição podem tomar um número infinito
de valores possíveis, existem devido a isso, uma infinidade de distribuições
normais com comportamentos diferentes.
Tendo a função de densidade de probabilidade uma expressão um pouco
elaborada, torna-se moroso fazer o cálculo de probabilidades através dessa
função. Assim, procede-se ao que se chama a normalização ou estandardização da variável inicial. Isso consiste em subtrair a variável inicial por µ e
dividir por σ. Então se a variável inicial X tem distribuição normal de parâmetros µ e σ, ou seja, se X „ N pµ; σq, calcula-se a variável transformada
, que é chamada a normal reduzida ou normal padrão.
Z tal que, Z “ X´µ
σ
5.3.5
Valor médio, valor esperado ou esperança matemática
E rZs “ E
„
Função densidade de probabilidade
A função de densidade de probabilidade da normal padrão é dada por:
z2
1
e´ 2 ,
ϕ pzq “ ?
2π
com ´8 ă z ă `8.
5.3.8
Função de distribuição
A função de distribuição associada permite-nos calcular probabilidades em
determinados intervalos. Assim, temos,
żz
1
s2
?
Φ pzq “ P rZ ď zs “
e´ 2 ds.
2π
´8
Existe uma tabela para a função de distribuição da variável Z „ N p0; 1q.
Esta função representa-se por
ȷ
X ´µ
1
“ E rX ´ µs “
σ
σ
Φ pzq “ P rZ ď zs .
1
pE rXs ´ E rµsq “
“
σ
1
“
pµ ´ µq “
σ
“ 0.
Deste modo, o cálculo de probabilidades é feito da seguinte forma:
‰
` ˘
`
˘
“
ď Z ď b´µ
“ Φ b´µ
´ Φ a´µ
;
• P ra ď X ď bs “ P a´µ
σ
σ
σ
σ
“
‰
` a´µ ˘
a´µ
• P rX ď as “ P Z ď σ “ Φ σ ;
‰
`
˘
“
“ 1 ´ Φ a´µ
;
• P rX ą as “ 1 ´ P rX ď as “ 1 ´ P Z ď a´µ
σ
σ
e utilizando, em seguida, a tabela da função de distribuição da normal reduzida.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
51/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
52/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Como ϕ pzq é simétrica, tem-se que
com ai P R e i “ 1, . . . , n, tem distribuição normal com valor médio
Φ p´zq “ 1 ´ Φ pzq ,
µY “ a1 µ1 ` a2 µ2 ` ¨ ¨ ¨ ` an µn “
como se ilustra nas figuras seguintes:
n
ÿ
ai µi
i“1
e variância
Φ (z)
σY2 “ a21 σ12 ` a22 σ22 ` ¨ ¨ ¨ ` a2n σn2 “
z
0
D(z)=Φ(z)−Φ(−z)
z
0
a2i σi2 ,
i“1
ou seja,
Z
Y “
-z
n
ÿ
n
ÿ
i“1
ai Xi „ N
˜
n
ÿ
ai µi ;
i“1
d
n
ÿ
a2i σi2
i“1
¸
;
(b) Sejam X1 , X2 , . . . , Xn variáveis aleatórias independentes, cada uma com
distribuição normal com valor médio µ e variância σ 2 , ou seja, Xi „
N pµ; σq, com i “ 1, . . . , n. Então, a variável aleatória
Z
Y “ X1 ` X2 ` ¨ ¨ ¨ ` Xn “
n
ÿ
Xi
i“1
tem distribuição normal com valor médio
1−Φ (z)
Φ (−z)
-z
0
z
µY “ µ ` µ ` ¨ ¨ ¨ ` µ “ nµ
e variância
Z
ou seja,
Exemplo 5.3. Pretende-se calcular o valor da função de distribuição de X
no ponto 15, quando X „ N p10; 5q. “
‰
Logo, F p15q “ P rX ď 15s “ P X´10
ď 15´10
“ P rZ ď 1s “ Φ p1q “
5
5
0, 8413.
5.3.9
Aditividade da distribuição normal
(a) Sejam X1 , X2 , . . . , Xn variáveis aleatórias independentes, cada uma com
distribuição normal com valor médio µi e variância σi2 , ou seja, Xi „
N pµi ; σi q, com i “ 1, . . . , n. Então, a variável aleatória
Y “ a1 X1 ` a2 X2 ` ¨ ¨ ¨ ` an Xn “
n
ÿ
Y “
n
ÿ
i“1
´
¯
?
Xi „ N nµ; nσ 2 ;
(c) Sejam X1 , X2 , . . . , Xn variáveis aleatórias independentes, cada uma com
distribuição normal com valor médio µ e variância σ 2 , ou seja, Xi „
N pµ; σq, com i “ 1, . . . , n. Então, a variável aleatória
řn
Xi
X1 ` X2 ` ¨ ¨ ¨ ` Xn
“ i“1
X“
n
n
tem distribuição normal com valor médio
µX “
ai Xi ,
µ ` µ ` ¨¨¨` µ
nµ
“
“µ
n
n
i“1
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
σY2 “ σ 2 ` σ 2 ` ¨ ¨ ¨ ` σ 2 “ nσ 2 ,
53/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
54/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
e variância
ou seja,
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
(b) Admita que a agência bancária cumpre os seus objectivos, se o total
de depósitos efectuados numa semana (5 dias), exceder 760 unidades
monetárias. Qual é a probabilidade de numa semana a agência cumprir
os seus objectivos?
σ2 ` σ2 ` ¨ ¨ ¨ ` σ2
nσ 2
σ2
“ 2 “ ,
n2
n
n
řn
ˆ
˙
Xi
σ
X “ i“1
„ N µ; ?
.
n
n
2
σX
“
Exemplo 5.4. Uma fábrica produz 3 tipos de componentes eléctricas X, Y
e W cujos preços por unidade são 6e, 3e e 7e, respectivamente. A venda
(número de unidades vendidas por semana) de cada componente segue uma
distribuição normal, ou seja,
• componente X: N p190; 48q;
Consideremos a variável aleatória Y - “montante de depósitos efectuados em 5 dias numa agência bancária”.
Usando a ?
aditividade
`
˘ da
2 , ou
distribuição normal
tem-se,
Y
„
N
µ
“
5
ˆ
150;
σ
“
5
ˆ
10
? ˘
`
seja, Y „ N µ “ 750;
” σ “ 500 ı. Assim temos, P rY ą 760s “ 1 ´
P rY ď 760s “ 1 ´ P Z ď
760´750
?
500
“ 1 ´ Φ p0, 45q “ 0, 3264.
(c) Determine a probabilidade de em pelo menos duas semanas de um determinado mês (4 semanas), a agência cumprir os objectivos?
• componente Y : N p232; 64q;
• componente W : N p225; 60q.
Qual é a probabilidade da fábrica realizar mais de 3500e numa semana com
a venda das componentes?
Para calcular a probabilidade da fábrica realizar mais de 3500e numa
semana com a venda das componentes, temos de considerar a variável aleatória T “ 6X ` 3Y ` 7W para a qual, utilizando a aditividade da distribuição
normal, se tem:
• µ “ 6 ˆ 190 ` 3 ˆ 232 ` 7 ˆ 225 “ 3411;
?
• σ “ 62 ˆ 482 ` 32 ˆ 642 ` 72 ˆ 602 “ 544, 3;
isto é, T „ N pµ “ 3411;
” σ “ 544, 3q.ı Assim temos que P rT ą 3500s “ 1 ´
P rT ď 3500s “ 1 ´ P Z ď 3500´3411
“ 1 ´ Φ p0, 16q “ 1 ´ 0, 5636 “ 0, 4364.
544,3
Exemplo 5.5. O montante de depósitos efectuados diariamente numa agência bancária, é uma variável aleatória com distribuição normal de valor médio e desvio padrão de 150 e 10 unidades monetárias, respectivamente. Pode
considerar-se que os montantes depositados em dias diferentes são independentes.
Consideremos a variável aleatória W - “número de semanas, em 4, em
que a agência cumpre os objectivos” em que W „ b pw; n “ 4; p “ 0, 3264q,
onde p “ P rY ą 760s “ 0, 3264.
Então, P rW ě 2s “ 1 ´ P rW ă 2s “ 1 ´ p4C0 ˆ 0, 32640 ˆ 0, 67364`
4
C1 ˆ 0, 3264 ˆ 0, 67363q “ 0, 3951.
Exemplo 5.6. Uma fábrica de componentes electrónicos produz resistências
que têm resistência média de 100 ohms e um desvio padrão de 10 ohms. A
distribuição da resistência é normal. Determine a probabilidade de que uma
amostra aleatória de n “ 25 resistências, ter uma resistência média inferior
a 95 ohms.
Note que a distribuição amostral de X é normal, com média µX “ 100
ohms e desvio padrão de σX “ ?σn “ ?1025 “ 2.
Assim, a probabilidade desejada corresponde à área a sombreado da figura
seguinte:
σX = 2
(a) Qual é o montante cujo valor não é excedido em 95% dos dias?
95
100
X
Consideremos a variável aleatória X - “montante de depósitos efectuados diariamente numa agência bancária” tendo-se que
X „ N pµ “ 150; σ “ 10q .
“
‰
`
˘
P rX ď as “ 0, 95 ô P Z ď a´150
“ 0, 95 ô Φ a´150
“ 0, 95 ô
10
10
a´150
a´150
´1
“ Φ p0, 95q ô 10 “ 1, 645 ô a “ 166, 45 unidades monetá10
rias.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
55/62
“
‰
“
Assim tem-se P X ă 95 “ P Z ă
95´100
2
‰
“ P rZ ă ´2, 5s “ 0, 0062.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
56/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
6
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Teorema limite central
Observação 6.1. Observe-se que
O teorema limite central é um dos resultados mais importantes em Estatística e indica qual a distribuição de X (aproximadamente normal) desde que
a amostra seja suficientemente grande e a distribuição da população tenha
variância finita. A definição de suficientemente grande depende, evidentemente, da distribuição da população e do grau de aproximação pretendido.
Quanto mais assimétrica e afastada da normal for a população, maior terá
que ser o tamanho da amostra. No entanto, desde que as observações sejam
independentes, a aproximação à normal para X é geralmente satisfatória se
n ą 30, seja qual for a forma da distribuição. Para n ď 30, a aproximação
é satisfatória se a distribuição da população não diferir excessivamente da
distribuição normal.
Teorema 6.1. Seja X1 , X2 , . . . , Xn uma amostra aleatória independente identicamente distribuída (i.i.d.) de dimensão n, com E rXi s “ µ e V ar rXi s “
σ 2 , com i “ 1, . . . , n, e seja Y “ X1 ` X2 ` ¨ ¨ ¨ ` Xn . Então para valores
grandes de n pn ą 30q, a variável aleatória
Y ´ nµ
Z“ ?
nσ 2
converge em distribuição para a normal padrão ou normal estandardizada,
isto é, para n grande tem-se
Y ´ nµ
?
„N
9 p0, 1q .
nσ 2
Dividindo por n o numerador e o denominador da variável Z, obtém-se
Y
n
´µ
?σ
n
Observe-se que
„N
9 p0, 1q .
řn
Xi
Y
“ i“1
“ X.
n
n
Logo, pelo teorema limite central conclui-se que, se Xi , com i “ 1, . . . , n,
forem n variáveis aleatória independentes identicamente distribuídas, com
média µ e variância finita σ 2 , então a média amostral X, para amostras
grandes pn ą 30q, terá uma distribuição aproximadamente normal com média
2
µ e variância σn , ou seja,
X ´µ
?σ
n
C. Fernandes & P. Ramos
µX “
µX ` µX ` ¨ ¨ ¨ ` µX
“ µ Xi
n
e variância
σ2
σ2 ` σ2 ` ¨ ¨ ¨ ` σ2
“ X2i ,
n2
n
com i “ 1, . . . , n, se a amostra aleatória é retirada de uma população normal.
Se a amostra é retirada duma população com distribuição desconhecida, a
distribuição de X será aproximadamente normal com média µXi e variância
2
σX
“
2
σX
n
i
, se o tamanho da amostra for suficientemente grande.
Este teorema é interessante porque permite fazer inferência sobre a média
amostral, a partir de uma amostra suficientemente grande, sem se precisar
de conhecer a forma da distribuição da população. O teorema limite central
também justifica o uso da aproximação normal para calcular probabilidades
de distribuições discretas, como por exemplo, as distribuições binomial e de
Poisson. Conforme referimos, os resultados referentes à média e variância
de X e o teorema limite central, são válidos apenas para amostras aleatórias independentes identicamente distribuídas: amostragem aleatória de uma
população infinita ou amostragem aleatória de uma população finita com reposição. No entanto, mesmo quando a amostragem é de uma população finita
e sem reposição, é razoável admitir a validade destes resultados, desde que
o tamanho da amostra, n, seja pequeno quando comparado com o tamanho
da população, N.
Exemplo 6.1. Suponhamos que a variável aleatória X tem distribuição uniforme contínua,
" 1
, se 4 ď x ď 6
.
f pxq “ 2
0 , outros casos
Encontre a distribuição da média amostral da amostra aleatória de tamanho n “ 40.
2
A média e a variância de X são µ “ 6`4
“ 5 e σ 2 “ p6´4q
“ 31 ,
2
12
respectivamente. Pelo teorema limite central temos:
?σ
n
57/62
X1 ` X2 ` ¨ ¨ ¨ ` Xn
n
tem distribuição normal com média
X ´µ
„N
9 p0, 1q .
Variáveis aleatórias e modelos teóricos unidimensionais
X“
“
X ´5
X ´5
?1 “ b
„
9 Normal p0; 1q ,
?
3
40
1
120
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
58/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
pelo que a distribuição da média amostral da amostra aleatória
b é aproxima1
damente normal com média µX “ 5 e desvio padrão σX “ 120
.
As distribuições de X e de X são apresentadas nas figuras seguintes:
σ2X = 1
120
4
5
6
X
4
5
6
X
Exemplo 6.2. Na confecção de uma determinada peça de roupa, o desperdício de tecido resultante do corte automático para cada peça, tem comprimento
que varia uniformemente entre 0cm e 25cm, sendo a largura fixa. Calcule a
probabilidade do comprimento total desperdiçado no corte de tecido para 60
peças se situar entre 747cm e 752cm.
Consideremos a variável aleatória X - “comprimento do desperdício de
tecido resultante do corte automático de tecido para cada peça” em que X „
U p0; 25q. Consideremos agora a variável aleatória Y - “comprimento total
de tecido
ř desperdiçado no corte automático de tecido para 60 peças”, ou seja,
Y “ 60
i“1 Xi . Como a variável segue uma distribuição uniforme tem-se,
2
E rXs “ 25
“ 12, 5 e V ar rXs “ 25
“ 52, 08. Como o tamanho da amostra
2
12
é superior a 30 peças podemos utilizar o teorema limite central. Assim, temse que:
• µ “ 60 ˆ 12, 5 “ 750;
?
• σ “ 60 ˆ 52, 08 “ 55, 9
Para n pequeno, as probabilidades associadas a uma variável aleatória binomial, X „ b pn; pq, são facilmente calculadas através da fórmula exacta:
" n
Cx px p1 ´ pqn´x , se x “ 0, 1, 2, . . . , n
P rX “ xs “ f pxq “
.
0
, outros valores
Para n grande, torna-se mais fácil usar aproximações, se por exemplo,
não tivermos um computador nem uma calculadora à mão.
A distribuição normal, apesar de ser uma distribuição contínua, é frequentemente uma aproximação razoável duma distribuição discreta, quando
esta tem a forma de sino e é simétrica. Em particular, algumas distribuições,
como a binomial e a de Poisson, convergem para a normal, quando os seus
parâmetros se aproximam de certos valores limite. Além disso, como a distribuição normal é facilmente tabelada, é uma aproximação muito conveniente.
6.1.1
Distribuição normal como aproximação da distribuição binomial
A distribuição normal é utilizada como distribuição aproximada da distribuição binomial sempre que n ą 20 e np ě 5, embora a aproximação seja tanto
melhor quanto maior for n.
Se X „ b pn; pq, com n Ñ `8 e np ě 5, em termos práticos quando
n ą 20, então
?
X „N
9 pµ “ np; σ “ npqq ,
X ´ np
„N
9 p0; 1q .
?
npq
Este resultado é uma consequência do teorema limite central.
6.1.2
pelo que a distribuição da variável aleatória Y é aproximadamente normal
com média µY “ 750 e desvio padrão σY “ 55,” 9.
ı
Então tem-se que P r747 ď Y ď 752s “ P 747´750
ď Z ď 752´750
“
55,9
55,9
“ Φ p0, 04q ´ Φ p´0, 05q “ 0, 0359.
C. Fernandes & P. Ramos
Distribuição normal e a sua aproximação à binomial
e à de Poisson
ou seja,
podendo escrever-se
řn
ř60
Xi ´ nµ
Xi ´ 750
Y ´ nµ
?
„
9 Normal p0; 1q ,
“ i“1?
“ i“1
2
2
55, 9
nσ
nσ
Variáveis aleatórias e modelos teóricos unidimensionais
6.1
59/62
Distribuição normal como aproximação da distribuição de
Poisson
A distribuição normal é utilizada como distribuição aproximada da distribuição de Poisson sempre que λ ą 20, embora a aproximação seja tanto melhor
quanto maior for λ.
Se X „ P pλq, com λ Ñ `8, em termos práticos quando λ ą 20, então
´ ? ¯
X „N
9
λ; λ ,
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
60/62
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
Instituto Superior de Engenharia de Lisboa
Área Departamental de Matemática
Resumos sobre Probabilidades e Estatística
ou seja,
X ´λ
? „N
9 p0; 1q .
λ
Este resultado é uma consequência do teorema limite central.
6.1.3
Correcção da continuidade
A aproximação à distribuição normal de uma distribuição discreta, tem de
ser efectuada tendo em conta que a distribuição normal é uma distribuição
contínua. Ou seja, o acontecimento X “ x, no caso discreto, tem de ser
reescrito como x´ ε ď X ď x` ε, no caso contínuo, visto que P rX “ xs “ 0,
quando X é uma variável aleatória contínua. Como os valores discretos
consecutivos distam de uma unidade, escolhemos ε “ 0, 5. Isto é o que se
designa por correcção de continuidade, cujo objectivo é reduzir o erro de
aproximação.
Exemplo 6.4. O número de avarias que uma máquina tem por dia, é uma
variável aleatória com distribuição de Poisson de valor médio 0, 2. Calcule
um valor aproximado para a probabilidade da referida máquina ter durante
um ano (365 dias) exactamente 75 avarias.
Consideremos a variável aleatória X - “número de avarias que a máquina tem por dia”, em que X „ P pλ “ 0, 2q. Considerando a variável
aleatória X 1 - “número de avarias que a máquina tem por ano”, temos que
X 1 „ P pλ “ 0, 2 ˆ 365 “ 73q. Como λ ą 20, podemos
fazer?a aproximação
`
˘
à distribuição normal. Assim temos que X „N
9
µ “ 73; σ “ 73 .
A probabilidade pretendida é P rX “ 75s. Usando a correcção de continuidade
temos que P r75
”
ı ´ 0, 5 ď X ď 75 ` 0, 5s “ P r74, 5 ď X ď 75, 5s “
75,5´73
?
?
P 74,5´73
“ Φ p0, 29q ´ Φ p0, 18q “ 0, 0427.
ď
Z
ď
73
73
Definição 6.1. Seja X uma variável aleatória discreta. A correcção de continuidade consiste em converter X numa variável aleatória contínua, reescrevendo o acontecimento x1 ď X ď x2 como x1 ´ 0, 5 ď X ď x2 ` 0, 5
e calculando P rx1 ´ 0, 5 ď X ď x2 ` 0, 5s a partir da função densidade de
probabilidade.
Exemplo 6.3. Numa determinada cidade, a taxa de desemprego é de 11%.
Tendo-se recolhido uma amostra de 300 pessoas, aptas para o trabalho, calcule
um valor aproximado para a probabilidade de:
(a) haver no máximo 17 desempregados na amostra recolhida;
Consideremos a variável aleatória X - “número de desempregados em
300 pessoas”, tendo-se que X „ b pn “ 300; p “ 0, 11q. Como o tamanho da amostra é superior a 20 e np “ 33 ě 5, podemos fazer a
aproximação à distribuição normal. Temos que?E rXs “ np “ 33 e
V ar rXs “ npq “ 29, 3, logo X „N
9 pµ “ 33; σ “ 29, 3q.
A probabilidade pretendida é P rX ď 17s. Usando a correcção
de conti”
ı
?
nuidade temos P rX ď 17 ` 0, 5s “ P rX ď 17, 5s “ P Z ď 17,5´33
“
29,3
Φ p´2, 86q “ 0, 0021.
(b) haver mais de 30 desempregados na amostra referida.
A probabilidade pretendida é P rX ě 31s. Usando a correcção
de conti-ı
”
?
nuidade temos P rX ě 31 ´ 0, 5s “ P rX ě 30, 5s “ 1´P Z ă 30,5´33
29,3
“ 1 ´ Φ p´0, 46q “ 0, 6772.
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
61/62
Variáveis aleatórias e modelos teóricos unidimensionais
C. Fernandes & P. Ramos
62/62