219 Estudo da estrutura e da composição interna das estrelas de

Estudo da estrutura e da composição interna das estrelas de nêutrons
Paula M. G. L. Ferreira, German Lugones
Centro CCNH Universidade Federal do ABC
Av. dos Estados, 5001, Santo André, SP
[email protected], [email protected]
Resumo. Neste trabalho utilizamos as equações da estrutura estelar relativística para descrever estrelas de nêutrons e estrelas de quarks.
Utilizamos as equações de estado de Bethe-Johnson e de Baym-Pethick-Sutherland para descrever estrelas de nêutrons e o modelo sacola
do M.I.T. para descrever estrelas de quarks. A relação “massa-raio” é qualitativamente diferente em ambos os casos. Isto mostra que é
possível inferir a composição interna das estrelas compactas a partir de determinações observacionais da massa e o raio destas estrelas.
Palavras-chave. Estrela de nêutrons, Equações de T.O.V.
I. INTRODUÇÃO
II. DESENVOLVIMENTO
s estrelas de nêutrons são sustentadas contra a pressão
gravitacional através da pressão de degenerescência dos
nêutrons contidos no seu interior. Para descrever a estrutura
das estrelas, podemos utilizar as equações da relatividade geral
conhecidas como equações de Tolman-Oppenheimer-Volkoff
(TOV) [1]. Essas equações são deduzidas dentro do
formalismo da relatividade geral, a partir das equações de
campo de Einstein, considerando-se a estrela como uma
distribuição de matéria relativística, esfericamente simétrica,
estática e composta por matéria que se comporta como um
fluido perfeito. As equações de TOV possuem a seguinte
forma:
Nesse trabalho calculamos o raio da estrela de acordo com sua
pressão central utilizando o software Wolfram Mathematica
7.0. O programa integra repetidamente as equações de TOV
até que encontre o raio da estrela (local onde a pressão é nula).
E assim construímos os gráficos onde relacionamos a massa
de uma estrela de nêutrons com o seu respectivo raio.
A
III. RESULTADOS E DISCUSSÃO
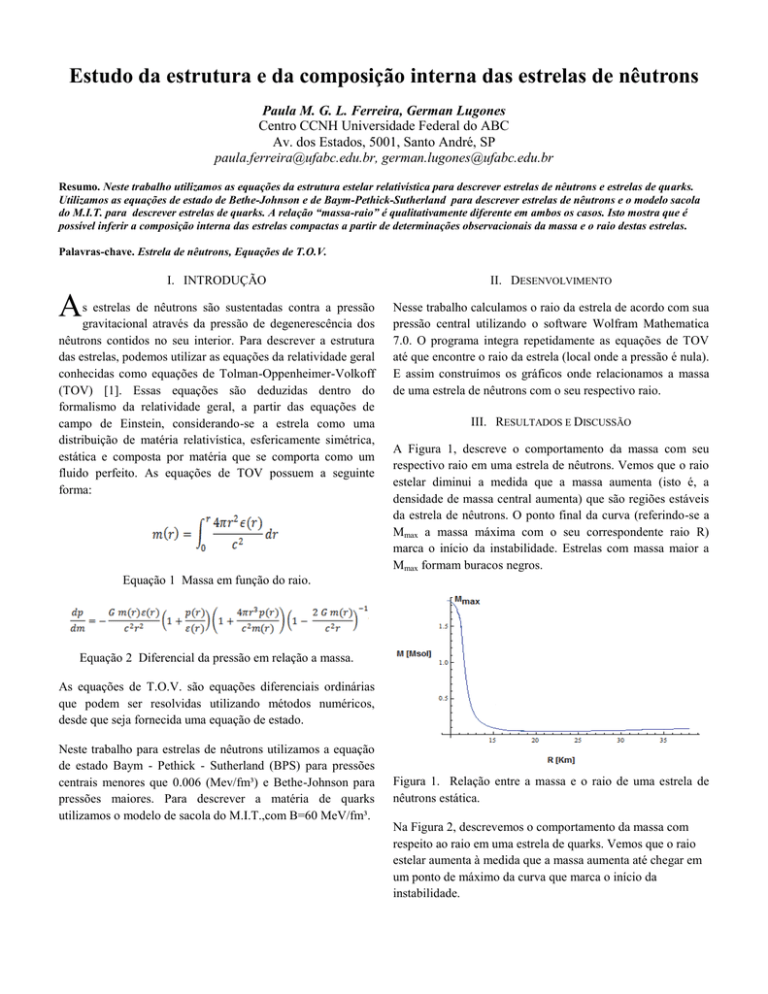
A Figura 1, descreve o comportamento da massa com seu
respectivo raio em uma estrela de nêutrons. Vemos que o raio
estelar diminui a medida que a massa aumenta (isto é, a
densidade de massa central aumenta) que são regiões estáveis
da estrela de nêutrons. O ponto final da curva (referindo-se a
Mmax a massa máxima com o seu correspondente raio R)
marca o início da instabilidade. Estrelas com massa maior a
Mmax formam buracos negros.
Equação 1 Massa em função do raio.
Equação 2 Diferencial da pressão em relação a massa.
As equações de T.O.V. são equações diferenciais ordinárias
que podem ser resolvidas utilizando métodos numéricos,
desde que seja fornecida uma equação de estado.
Neste trabalho para estrelas de nêutrons utilizamos a equação
de estado Baym - Pethick - Sutherland (BPS) para pressões
centrais menores que 0.006 (Mev/fm³) e Bethe-Johnson para
pressões maiores. Para descrever a matéria de quarks
utilizamos o modelo de sacola do M.I.T.,com B=60 MeV/fm³.
Figura 1. Relação entre a massa e o raio de uma estrela de
nêutrons estática.
Na Figura 2, descrevemos o comportamento da massa com
respeito ao raio em uma estrela de quarks. Vemos que o raio
estelar aumenta à medida que a massa aumenta até chegar em
um ponto de máximo da curva que marca o início da
instabilidade.
Figura 2. Relação entre a massa e o raio de uma estrela de
quarks.
IV. CONCLUSÃO
Com base nos resultados obtidos pelo modelo proposto
concluímos que a massa máxima para uma estrela de nêutrons
é aproximadamente 1,8 massas solares e o raio máximo para
uma estrela de quarks é aproximadamente 11 km. Esses dados
estão
de
acordo
com
os
valores
observados
experimentalmente.
Vimos que em uma estrela de nêutrons, a massa se mostra
inversamente proporcional ao raio enquanto, em uma estrela
de quarks a massa se mostra proporcional ao raio. Logo,
podemos inferir a composição interna das estrelas compactas
através da determinação da relação “massa-raio” que é
qualitativamente distinta em ambos os casos.
REFERÊNCIAS
[1]
Shapiro, S. L. & Teukolsky S. A. Black Holes, White Dwarfs and
Neutron Stars: The Physics
AGRADECIMENTOS
Ao Programa de Iniciação Científica da
(PIC/UFABC) pelo financiamento deste trabalho.
UFABC