Se a um ângulo não raso. O con unto dos pontos do

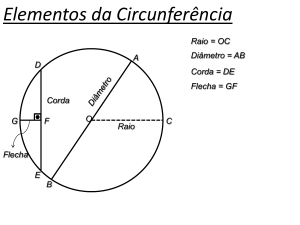
GEOMETRIA EUCLIDIANA I
AULA 06: CIRCUNFERÊNCIA
TÓPICO 06: ÂNGULOS DE UMA CIRCUNFERÊNCIA
DEFINIÇÃO 10:
Seja
um ângulo não raso. O conjunto dos pontos do plano não
pertencentes
mais os lados de chamaremos de ângulo côncavo de lados
e
e de vértice O, o qual representaremos por
(clique aqui para
abrir) .
Definimos a medida de
Note que 180º < |
como se segue: |
|= 360 - |
|.
| < 360º e que, de fato, um ângulo côncavo é
uma região côncava do plano.
Note também que os ângulos que até então considerávamos eram
figuras convexas.
DEFINIÇÃO 11:
Chama-se ângulo central de uma circunferência qualquer ângulo côncavo ou
convexo cujo vértice é o centro da circunferência
DEFINIÇÃO 12:
Chama-se arco a interseção de um ângulo central com a circunferência
(clique aqui para abrir ).
Se A e B são os pontos dos lados do ângulo central pertencentes à
circunferência e C é um ponto distinto de A e de B pertencente ao arco,
então este será denotado por
Definimos a medida do arco
ou simplesmente por
e a indicamos por |
medida do ângulo central associado (
ou
| como sendo a
). Chamamos de
arco menor
aquele associado ao ângulo central convexo
arco maior
aquele associado ao ângulo central côncavo
Chama-se semi-circunferência todo arco
e de
.
cuja medida é 180º
DEFINIÇÃO 13:
Um ângulo convexo é dito inscrito em uma circunferência α se seu vértice
pertence a α e as retas que contêm seus lados são secantes a α.
DEFINIÇÃO 14:
A cada ângulo inscrito
numa circunferência α em que B,C
∈Α
associamos um arco, a saber: o arco
que não contém A, e, a cada ângulo
semi-inscrito
associamos o arco que é a interseção do próprio ângulo
com α.
Se um arco está associado a um ângulo inscrito ou semi-inscrito, dizemos
que o ÂNGULO SUBTENDE O ARCO.
Um ângulo convexo é dito semi-inscrito em uma circunferência α se seu
vértice pertence a α e a reta que contém um de seus lados é secante e a que
contém o outro é tangente a α.
OLHANDO DE PERTO
Observe que todo ângulo inscrito ou semi-inscrito numa circunferência é
não raso.
Responsável: Professor José Aílton Forte Feitosa
Universidade Federal do Ceará - Instituto UFC Virtual