Faculdade de Ciências Departamento de Matemática

Faculdade de Ciências
Departamento de Matemática e Informática
Licenciatura em Informática, Diurno
2
0
Teste de Fundamentos de Geometria. Guião da Correcção.
Duração: 90 minutos
25.04.2016
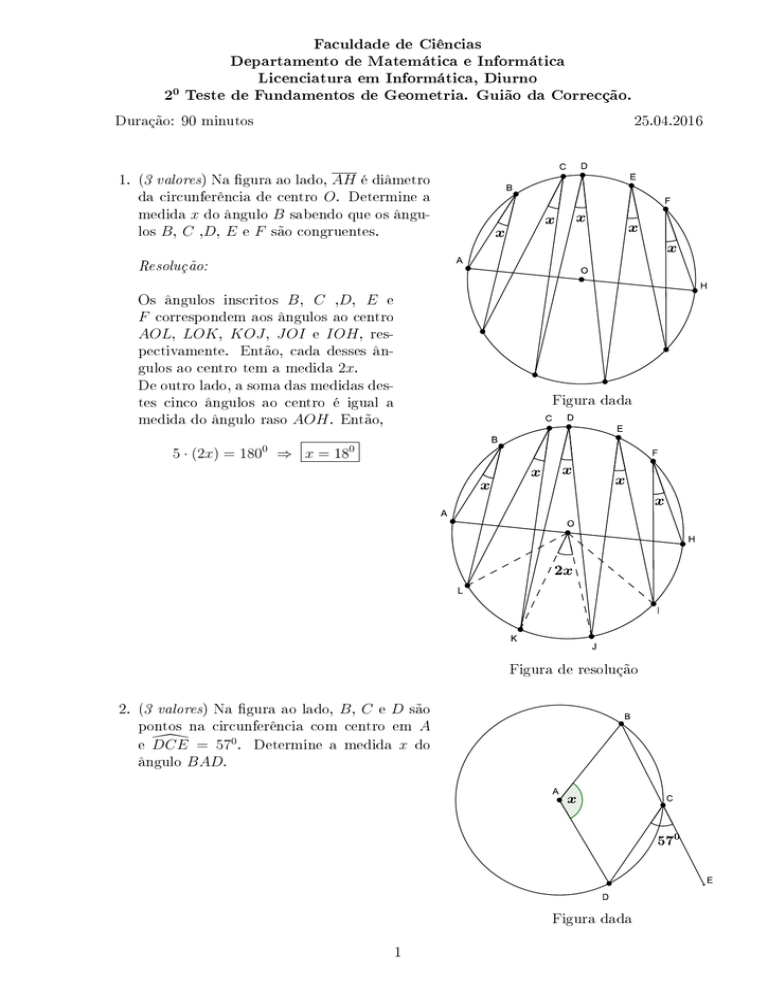
1. (3 valores) Na gura ao lado, AH é diâmetro
da circunferência de centro O. Determine a
medida x do ângulo B sabendo que os ângulos B , C ,D, E e F são congruentes.
Resolução:
Os ângulos inscritos B , C ,D, E e
F correspondem aos ângulos ao centro
AOL, LOK , KOJ , JOI e IOH , respectivamente. Então, cada desses ângulos ao centro tem a medida 2x.
De outro lado, a soma das medidas destes cinco ângulos ao centro é igual a
medida do ângulo raso AOH . Então,
Figura dada
5 · (2x) = 1800 ⇒ x = 180
Figura de resolução
2. (3 valores) Na gura ao lado, B , C e D são
pontos na circunferência com centro em A
\ = 570 . Determine a medida x do
e DCE
ângulo BAD.
Figura dada
1
Resolução:
Os ângulos DCE e BCD são suplementares, então
\ = 1800 − 570 = 1230
BCD
O ângulo ao centro que corresponde ao
ângulo inscrito BCD mede
2 · 1230 = 2460
(veja a gura de resolução). Mas
a soma das medidas deste ângulo ao
cento e do ∠BAD é igual a medida do
ângulo giro. Temos
Figura de resolução
2460 + x = 3600 ⇒ x = 1140
3. (3.5 valores) Um quadrilátero ABCD cuja área é igual a S1 é circunscrito ao círculo
cuja área é igual a S0 , sendo |CD| = 2|AB|. Demonstre que
√
π S1
.
|AB| = √
3 S0
1) Designemos por r o raio da
circunferência e por x a medida do lado AB .
Temos
Resolução:
|AB| + |CD| = x + 2x = 3x,
e pela uma propriedade de quadrilátero circunscrito a uma circunferência
|BC| + |AD| = |AB| + |CD| = 3x.
Então, o perímetro P do quadrilátero é igual a
Figura de resolução
P = |BC| + |AD| + |AB| + |CD| = 6x.
2) Exprimimos o raio por S0 :
S0 = πr
2
√
S0
r= √ .
π
⇒
3) A medida da apótema é igual a r. Então, pela fórmula conhecida da área dim polígono
circunscrito temos
√
√
P
6x
S0
3 S0 x
S1 = r =
· √ = √
2
2
π
π
2
⇒
√
π S1
|AB| = x = √ ,
3 S0
c.q.d.
4. (3.5 valores) Na gura ao lado, cada circunferência tem o raio de 1 cm. Determine a
área da gura sombreada.
Resolução:
Designemos por A, B e C os centros das circunferências, e por D ponto médio de BC .
O 4ABC é equilátero com medida de lado 2
cm.
A área S da gura sombreada calcula-se pela
fórmula
S = S4 − 3S1
(1)
onde S4 é área do 4ABC e S1 a área do
sector circular de raio 1 cm que corresponde
ao ângulo ao centro de 600 .
A mediana AD do 4ABC também é altura.
Do 4ABD, pelo teorema de Pitágoras, temos
Figura dada
|AB|2 = |AD|2 + |BD|2 ⇒√
22 = |AD|2 + 12 ⇒ |AD| = 3 cm.
Então, pela fórmula conhecida da área de triângulo:
√
√
1
1
S4 = |BC| |AD| = · 2 · 3 = 3 cm2 .
2
2
(2)
Pela fórmula conhecida da área de sector circular, temos:
S1 =
π
π|CD|2 · 600
= cm2 .
0
360
6
Figura de resolução
(3)
Substituindo as expressões (2) e (3) para (1) obtemos:
S=
√
3−3·
π
6
⇒
S=
√
π
3 − cm2
2
5. (3 valores) Sejam A(−2; 1) e B(0, −3). Determine C(x, y) em seguintes suposições: os
−→ −−→
−→
vectores CA e BC têm a mesma direcção, os sentidos contrários e o módulo de CA é
−−→
igual a metade do módulo de BC .
Resolução: Sabendo a interpretação geométrica do produto dum vector por um número,
−→
−−→
−→ −−→
concluímos que CA = − 12 BC , ou, o que é equivalente, 2CA = CB.
−→
−−→
Escrevemos os vectores CA e CB na forma coordenada:
−→
CA = (xA − xC ; yA − yC ) = (−2 − x; 1 − y),
−→
−−→
−−→
CB = (xB − xC ; yB − yC ) = (−x; −3 − y).
Escrevemos a igualdade 2CA = CB na forma coordenada e determinemos as coordena3
das do ponto C :
2·(−2−x; 1−y) = (−x; −3−y) ⇒
−4 − 2x = −x
2 − 2y = −3 − y
⇒
x = −4
y=5
⇒ C(−4; 5)
−
) No sistema de coordenadas são apresentados o ponto A e os vectores →
a e
→
−
→
− −
→
→
−
b . No mesmo sistema, construa o vector u = b − 2a ao seleccionar o ponto A como
−
a origem do vector →
u.
6. (2
valores
−−→
−−→
−
−
7. (2 valores) Seja D o ponto médio do lado AB do 4ABC . Sejam →
u = CD e →
v = BC .
−→
→
−
→
−
Determine o vector CA em função de u e v .
Resolução: Pela regra de sequência,
−→ −−→ −→
−−→
−−→
−
−
CA = CB + BA = −BC − 2AD = −→
v − 2→
u.
Resposta:
−→
−
−
CA = −2→
u −→
v
Professores Yury Nepomnyashchikh e Clarinda Nhangumbe
4