Teorema do Valor Médio

Universidade Tecnológica Federal do Paraná – Câmpus Cornélio Procópio
Notas de aula: Prof. Me. Armando P. Silva
Teorema do Valor Médio e Teorema de Rolle
Teorema do Valor Médio
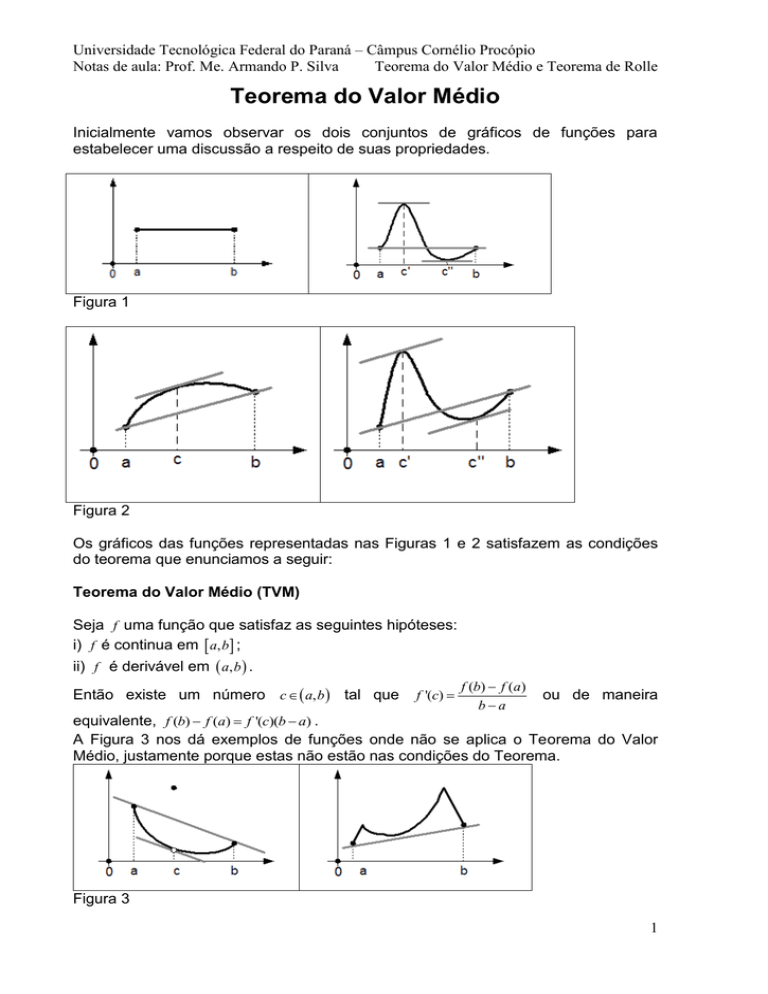
Inicialmente vamos observar os dois conjuntos de gráficos de funções para
estabelecer uma discussão a respeito de suas propriedades.
Figura 1
Figura 2
Os gráficos das funções representadas nas Figuras 1 e 2 satisfazem as condições
do teorema que enunciamos a seguir:
Teorema do Valor Médio (TVM)
Seja f uma função que satisfaz as seguintes hipóteses:
i) f é continua em  a, b ;
ii) f é derivável em  a, b  .
Então existe um número c   a, b  tal que
f '(c) 
f (b)  f (a)
ba
ou de maneira
equivalente, f (b)  f (a)  f '(c)(b  a) .
A Figura 3 nos dá exemplos de funções onde não se aplica o Teorema do Valor
Médio, justamente porque estas não estão nas condições do Teorema.
Figura 3
1
Universidade Tecnológica Federal do Paraná – Câmpus Cornélio Procópio
Notas de aula: Prof. Me. Armando P. Silva
Teorema do Valor Médio e Teorema de Rolle
Para compreender o significado do Teorema do Valor Médio faremos uma analogia
com a seguinte situação:
Se a média de velocidade, em uma viagem de carro de uma cidade a outra, é de
80Km/h, então em algum momento da viagem o velocímetro do carro deve ter
marcado 80Km/h. Fazendo uma leitura em termos matemáticos, seja s(t ) a posição
do carro em cada instante t . Se a viagem começa em t  a (horas) e termina em
t  b (horas), a velocidade média é dada por: vM (t ) 
s(b)  s(a)
.
ba
A afirmação de que em algum momento da viagem a velocidade instantânea deve
ser igual a velocidade média, significa que em algum tempo t * tem-se
vM (t ) 
s(b)  s(a)
 v(t * )  s '(t * ) .
ba
Dando interpretação similar, porém, agora observando o conjunto de gráficos da
Figura 1, podemos perceber que se a função de posição s(t ) de um objeto em
movimento passar pelo mesmo lugar um dois instantes diferentes, t  a e t  b então
s(a)  s(b) , o que indica que pelo menos uma vez no percurso, o objeto teve
velocidade instantânea nula.
Na verdade este resultado é dado pelo Teorema de Rolle. Nós o enunciaremos na
sequencia, também porque iremos utilizá-lo na demonstração do TVM.
O Teorema do Valor Médio estabelece as condições mínimas que uma função s
s(b)  s(a)
deve satisfazer para que a igualdade vM (t ) 
 v(t* )  s '(t* ) seja
ba
verdadeira.
Teorema de Rolle
Seja f uma função que satisfaz as seguintes hipótese:
i) f é continua em  a, b ;
ii) f é derivável em  a, b  ;
iii) f (a)  f (b) .
Então existe um número c   a, b  tal que f '(c)  0 .
Podemos observar que o conjunto de funções representadas graficamente na Figura
1 satisfaz as hipóteses do teorema de Rolle.
Demonstração do TVM
Vamos construir as funções S e g para compor a demonstração:
f (b)  f (a)
( x  a) , x   a, b , cujo gráfico é a reta secante ao gráfico
ba
de f passando pelos pontos  a, f (a)  e  b, f (b)  e

S ( x)  f ( a ) 
2
Universidade Tecnológica Federal do Paraná – Câmpus Cornélio Procópio
Notas de aula: Prof. Me. Armando P. Silva
Teorema do Valor Médio e Teorema de Rolle

g ( x)  f ( x)  S ( x) , com x   a, b note que a função g assim definida, mede,
para cada x   a, b , a distância vertical entre os pontos ( x, f ( x)) no gráfico de f e
( x, g ( x)) na reta secante S . Veja que g (a)  g (b)  0 .
A função g satisfaz as condições do teorema de Rolle, então, existe c   a, b  tal que
g '(c)  0 .
Além
g '( x)  f '( x) 
disso,
g '( x)  f '( x)  S '( x)
f (b)  f (a)
.
ba
Para x  c , g '(c)  f '(c) 
e
S '( x) 
f (b)  f (a)
,
ba
assim,
f (b)  f (a)
 0 . Portanto, f (b)  f (a)  f '(c)(b  a) .
ba
Geometricamente, podemos perceber que a reta tangente ao gráfico de f
é paralela ao segmento da reta secante em  a, b exatamente em um ponto em que
a função g atinge o seu maior valor.
Consequências do Teorema do Valor Médio
A primeira consequência é a recíproca do fato trivial de que a derivada de uma
função constante é igual à zero, ou seja, se a derivada de uma função é zero, a
função é constante. A princípio nada nos assegura que este fato seja verdadeiro.
Será que não poderia existir uma função desconhecida, estranha, e não constante
cuja derivada fosse zero? Bem, com o Teorema do Valor Médio podemos provar que
tal função estranha não existe.
Nos corolários que seguem consideramos f e g contínuas no intervalo fechado
 a, b e deriváveis em  a, b  .
Corolário 1 (Funções com derivada zero)
Se f '( x)  0 para todo x   a, b  , então f é uma função constante em  a, b , isto é,
existe um número real k, tal que, f ( x)  k , qualquer que seja o ponto x de  a, b .
Corolário 2 (Funções com derivadas iguais)
Se f '( x)  g '( x) , para todo x no intervalo  a, b  . Então, f e g diferem por uma
constante, isto é, existe um número real k , tal que, f ( x)  g ( x)  k , para todo
x   a, b  .
Interpretação Geométrica:
Como as duas funções f e g diferem por uma constante, o gráfico de f pode ser
obtido a partir do gráfico de g , ou vice-versa, por uma translação vertical. Além
3
Universidade Tecnológica Federal do Paraná – Câmpus Cornélio Procópio
Notas de aula: Prof. Me. Armando P. Silva
Teorema do Valor Médio e Teorema de Rolle
disso, como estas funções têm a mesma derivada em cada ponto x   a, b , seus
gráficos têm retas tangentes paralelas nos pontos correspondentes ( x, f ( x)) e
( x, g ( x)) . Por isso estes gráficos são ditos paralelos. Veja Figura 4:
f
g h
Figura 4
Observe que as retas tangentes correspondentes, de cada curva são paralelas, ou
seja, suas derivadas são iguais para todo x .
Corolário 3 (Funções crescentes e decrescentes)

Se f '( x)  0 para todo x   a, b , então f é uma função crescente em  a, b .

Se f '( x)  0 para todo x   a, b , então f é uma função decrescente em  a, b .
Corolário 4 (Teorema do Valor Médio generalizado)
Sejam f e g contínuas em  a, b e deriváveis em  a, b  e suponha além disso que
g '( x)  0 para a  x  b . Então existe pelo menos um c entre a e b tal que
f '(c) f (b)  f (a)

g '(c) g (b)  g (a)
1
4
Exercício: Mostre que a função f ( x)  x3  1 satisfaz as hipóteses do Teorema do
Valor Médio no intervalo [0, 2] e encontre todos os valores de c do intervalo (0, 2) ,
nos quais a reta tangente ao gráfico de f é paralela à reta secante que liga os
pontos (0, f (0)) e (2, f (2)) .
4