Módulo VIII - Curso Matemática Para Concursos II

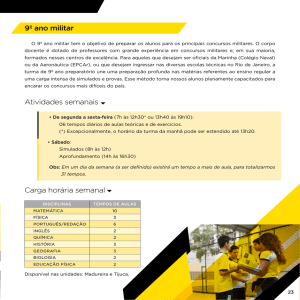
1
Curso Matemática Para Concursos II – Módulo VIII
Módulo VIII
Probabilidade: Espaço Amostral e Evento
Suponha que em uma urna existam cinco bolas vermelhas e uma branca.
Extraindo-se, ao acaso, uma das bolas, é mais provável que esta seja
vermelha. Isto significa que não saia a bola branca, mas que é mais fácil a
extração de uma vermelha. Os casos possíveis são seis:
Cinco são favoráveis à extração da bola vermelha. Dizemos que a
probabilidade da extração de uma bola vermelha é
5
1
e a bola branca .
6
6
Se as bolas da urna fossem todas vermelhas, a extração de uma
vermelha seria certa e de probabilidade igual a 1. Consequentemente, a
extração de uma bola branca seria impossível e de probabilidade igual a
zero.
Espaço amostral:
Dado um fenômeno aleatório, isto é, sujeito as leis do acaso, chamamos
espaço amostral ao conjunto de todos os resultados possíveis de
ocorrerem. Vamos indicá-lo pela letra E.
Exemplos:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
2
Curso Matemática Para Concursos II – Módulo VIII
Lançamento de um dado e observação da face voltada para cima:
E = {1, 2,3, 4,5, 6} .
Lançamento de uma moeda e observação da face voltada para cima:
E = {C , R} , onde C indica cara e R coroa.
Lançamento de duas moedas diferentes e observação das faces voltadas
para cima: E =
{( C , C ) , ( C , R ) , ( R, C ) , ( R, R )} .
Evento:
Chama-se evento a qualquer subconjunto do espaço amostral. Tomemos,
por exemplo, o lançamento de um dado:
• ocorrência do resultado 3: {3}
• ocorrência do resultado par: {2, 4, 6}
• ocorrência de resultado 1 até 6: E (evento certo)
• ocorrência de resultado maior que 6: ∅ (evento impossível)
Como evento é um conjunto, podemos aplicar-lhe as operações entre
conjuntos apresentados a seguir:
• união de dois eventos – Dados os eventos A e B, chama-se união de A
e B ao evento formado pelos resultados de A ou de B, indica-se por
A∪ B .
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
3
Curso Matemática Para Concursos II – Módulo VIII
• intersecção de dois eventos – Dados os eventos A e B, chama-se
intersecção de A e B ao evento formado pelos resultados de A e de B.
Indica-se por A ∩ B .
Se A ∩ B = ∅ , dizemos que os eventos A e B são mutuamente exclusivos,
isto é, a ocorrência de um deles elimina a possibilidade de ocorrência do
outro.
• evento complementar - Chama-se evento complementar do evento A
aquele formado pelos resultados que não são de A, indica-se A .
Aplicações
1) Considerar o experimento “registrar as faces voltadas para cima” em
três lançamentos de uma moeda.
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
4
Curso Matemática Para Concursos II – Módulo VIII
a) Quantos elementos tem o espaço amostral?
b) Escreva o espaço amostral?
Solução:
a) o espaço amostral têm 8 elementos, pois para cada lançamento temos
duas possibilidades e, assim: 2 ⋅ 2 ⋅ 2 = 8
b) E =
{( C , C , C ) , ( C.C.R ) , ( C , R, C ) , ( R, C , C ) , ( R, R, C ) , ( R, C , R ) , ( C , R, R ) , ( R, R, R}
2) Descrever o evento “obter pelo menos uma cara no lançamento de
duas moedas”.
Solução:
Cada elemento do evento será representado por um par ordenado.
Indicando o evento pela letra A, temos:
A=
{( C , R ) , ( R, C ) , ( C , C )}
3) Obter o número de elementos do evento “soma de pontos maior que 9
no lançamento de dois dados”.
Solução:
O evento pode ser tomado por pares ordenados com soma 10, soma 11
ou soma 12. Indicando o evento pela letra S, temos:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
5
Curso Matemática Para Concursos II – Módulo VIII
S=
{( 4, 6 ) , ( 5,5) , ( 6, 4 ) , ( 5, 6 ) , ( 6,5) , ( 6, 6 )} → n ( S )
= 6 elementos
4) Lançando-se um dado duas vezes, obter o número de elementos do
evento “número par no primeiro lançamento e soma dos pontos igual a
7”.
Solução:
Indicando o evento pela letra B, temos:
B=
{( 2,5) , ( 4,3) , ( 6,1)}
→ n ( B ) = 3 elementos
Probabilidade
Sendo n ( A ) o número de elementos do evento A, n ( E ) o número de
elementos do espaço amostral E
( A ⊂ E) , a
probabilidade de ocorrência
do evento A, que se indica por P ( A) , é o número real:
Observações:
1) Dizemos que n ( A ) é o número de casos favoráveis ao evento A e
n ( E ) o número de casos possíveis.
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
6
Curso Matemática Para Concursos II – Módulo VIII
2) Esta definição só vale se todos os elementos do espaço amostral
tiverem a mesma probabilidade.
3) A é o complemento do evento A.
Propriedades:
Aplicações
1) No lançamento de duas moedas, qual a probabilidade de obtermos
cara em ambas?
Solução:
Espaço amostral:
E=
{( C , C ) , ( C , R ) , ( R, C ) , ( R, R )} → n ( E ) = 4
Evento A: A =
Assim: P ( A ) =
{( C , C )} → n ( A) = 1
n ( A)
n(E)
=
1
4
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
7
Curso Matemática Para Concursos II – Módulo VIII
2) Jogando-se uma moeda três vezes, qual a probabilidade de se obter
cara pelo menos uma vez?
Solução:
E=
{( C , C , C ) , ( C , C , R ) , ( C , R, C ) , ( R, C , C ) , ( R, R, C ) , ( R, C, R ) , ( C , R, R ) , ( R, R, R )}
→ n(E) = 8
A =
{( C , C , C ) , ( C , C , R ) , ( C , R, C ) , ( R, C , C ) , ( R, R, C ) , ( R, C, R ) , ( C , R, R )}
→
n ( A) = 7
P ( A) =
n ( A)
n(E)
= P ( A) =
7
8
3) (Cesgranrio) Um prédio de três andares, com dois apartamentos por
andar, tem apenas três apartamentos ocupados. A probabilidade de
que cada um dos três andares tenha exatamente um apartamento
ocupado é:
a)
2
5
b)
3
5
c)
1
2
d)
1
3
e)
2
3
Solução:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
8
Curso Matemática Para Concursos II – Módulo VIII
O
número
n ( E ) = C6,3 =
de
elementos
do
espaço
amostral
é
dado
por:
6!
= 20
3!3!
O número de casos favoráveis é dado por n ( A ) = 2 ⋅ 2 ⋅ 2 = 8 , pois em cada
andar temos duas possibilidades para ocupá-lo. Portanto, a probabilidade
pedida é:
P ( A) =
n ( A)
n(E)
=
8 2
= (alternativa a)
20 5
4) Numa experiência, existem somente duas possibilidades para o
resultado. Se a probabilidade de um resultado é
1
, calcular a
3
probabilidade do outro, sabendo que eles são complementares.
Solução:
Indicando por A o evento que tem probabilidade
1
, vamos indicar por A o
3
1
outro evento. Se eles são P ( A) + P ( A ) = 1 → + P ( A ) = 1∴
3
5) No lançamento de um dado, qual a probabilidade de obtermos na face
voltada para cima um número primo?
Solução:
Espaço amostral: E = {1, 2,3, 4,5, 6} → n ( E ) = 6
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
9
Curso Matemática Para Concursos II – Módulo VIII
Evento A: A = {2,3,5} → n ( A) = 3
Assim: P ( A ) =
n ( A)
n(E)
=
3
1
→ P ( A) =
6
2
6) No lançamento de dois dados, qual a probabilidade de se obter soma
dos pontos igual a 10?
Solução:
Considere a tabela, a seguir, indicando a soma dos pontos:
Da tabela: n ( E ) = 36 e n ( A ) = 3
Assim: P ( A ) =
n ( A)
n(E)
=
3
1
=
36 12
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
10
Curso Matemática Para Concursos II – Módulo VIII
Adição de Probabilidades
Sendo A e B eventos do mesmo espaço amostral E, tem-se que:
“A probabilidade da união de dois eventos A e B é igual à soma das
probabilidades de A e B, menos a probabilidade da intersecção de A com
B”.
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
11
Curso Matemática Para Concursos II – Módulo VIII
Justificativa:
Sendo n ( A ∪ B ) e n ( A ∩ B ) o número de elementos dos eventos A ∪ B e
A ∩ B , temos que:
n ( A ∪ B ) = n ( A) + n ( B ) − n ( A ∩ B ) →
n ( A ∪ B)
n(E)
=
n ( A)
n(E)
+
n(B)
n(E)
−
n ( A ∩ B)
n(E)
∴
∴ P ( A ∪ B ) = P ( A) + P ( B ) − P ( A ∩ B )
Observação:
Se A e B são eventos mutuamente exclusivos, isto é:
A ∩ B = ∅ , então, P ( A ∪ B ) = P ( A ) + P ( B ) .
Aplicações:
1) Uma urna contém 2 bolas brancas, 3 verdes e 4 azuis. Retirando-se
uma bola da urna, qual a probabilidade de que ela seja branca ou verde?
Solução:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
12
Curso Matemática Para Concursos II – Módulo VIII
Número de bolas brancas: n ( B ) = 2
Número de bolas verdes: n (V ) = 3
Número de bolas azuis: n ( A ) = 4
A probabilidade de obtermos uma bola branca ou uma bola verde é dada
por:
P ( B ∪ V ) = P ( B ) + P (V ) − P ( B ∩ V )
Porém, P ( B ∩ V ) = 0, pois o evento bola branca e o evento bola verde
são mutuamente exclusivos.
Logo: P ( B ∪ V ) = P ( B ) + P (V ) , ou seja:
P ( B ∪V ) =
2 3
5
+ → P ( B ∪V ) =
9 9
9
2) Jogando-se um dado, qual a probabilidade de se obter o número 4 ou
um número par?
Solução:
O número de elementos do evento número 4 é n ( A ) = 1 .
O número de elementos do evento número par é n ( B ) = 3 .
Observando que n ( A ∩ B ) = 1 , temos:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
13
Curso Matemática Para Concursos II – Módulo VIII
P ( A ∪ B ) = P ( A) + P ( B ) − P ( A ∩ B ) →
P ( A ∪ B) =
1 3 1 3
1
+ − = ∴ P ( A ∪ B) =
6 6 6 6
2
3) A probabilidade de que a população atual de um país seja de 110
milhões ou mais é de 95%. A probabilidade de ser 110 milhões ou menos
é 8%. Calcular a probabilidade de ser 110 milhões.
Solução:
Temos P ( A) = 95% e P ( B ) = 8% .
A probabilidade de ser 110 milhões é P ( A ∩ B ) . Observando que
P ( A ∪ B ) = 100% , temos:
P ( A ∪ B ) = P ( A) + P ( B ) − P ( A ∩ B ) → 100% = 95% + 8% − P ( A ∩ B ) ∴
( A ∩ B ) = 3%
Probabilidade Condicional
Muitas vezes, o fato de sabermos que certo evento ocorreu modifica a
( A)
probabilidade que atribuímos a outro evento. Indicaremos por P B
a
probabilidade do evento B, tendo ocorrido o evento A (probabilidade
condicional de B em relação a A). Podemos escrever:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
14
Curso Matemática Para Concursos II – Módulo VIII
Multiplicação de probabilidades:
A probabilidade da intersecção de dois eventos A e B é igual ao produto
da probabilidade de um deles pela probabilidade do outro em relação ao
primeiro.
Justificativa:
n( A ∩ B)
n( A ∩ B)
n(E)
P B =
→P B =
∴
A
A
n ( A)
n ( A)
n(E)
( )
( )
( A) = P (PA(∩A)B )
P ( A ∩ B ) = P ( A) ⋅ P ( B )
A
∴P B
Analogamente:
( B)
P ( A ∩ B) = P ( B) ⋅ P A
Eventos independentes:
Dois eventos A e B são independentes se, e somente se:
( B ) = P ( A) ou P ( B A) = P ( B )
P A
( A) , e se A e B forem independentes,
Da relação P ( A ∩ B ) = P ( A) ⋅ P B
temos:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
15
Curso Matemática Para Concursos II – Módulo VIII
Aplicações:
1) Escolhida uma carta de baralho de 52 cartas e sabendo-se que esta
carta é de outros, qual a probabilidade de ser dama?
Solução:
Um baralho com 52 cartas tem 13 cartas de ouro, 13 de copas, 13 de
paus e 13 de espadas, tendo uma dama de cada naipe.
Observe que queremos a probabilidade de a carta ser uma dama de ouros
num novo espaço amostral modificado, que é o das cartas de ouros.
Chamando de:
• evento A : cartas de ouros
• evento B : dama
• evento A ∩ B : dama de ouros
Temos:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
16
Curso Matemática Para Concursos II – Módulo VIII
2) Jogando-se um dado e uma moeda. Dê a probabilidade de obtermos
cara na moeda e o número 5 no dado.
Solução:
Evento A: A = {C} → n ( A ) = 1
Evento B: B = {5} → n ( B ) = 1
Sendo A e B eventos independentes, temos:
P ( A ∩ B ) = P ( A) ⋅ P ( B ) → P ( A ∩ B ) =
P ( A ∩ B) =
1 1
⋅ ∴
2 6
1
12
3) (Cesgranrio) Um juiz de futebol possui três cartões no bolso. Um é todo
amarelo, outro é todo vermelho, e o terceiro é vermelho de um lado e
amarelo do outro. Num determinado lance, o juiz retira, ao acaso, um
cartão do bolso e mostra a um jogador. A probabilidade de a face que o
juiz vê ser vermelha e de a outra face, mostrada ao jogador, ser amarela
é:
a)
1
2
b)
2
5
c)
1
5
d)
2
3
e)
1
6
Solução:
Evento A: cartão com as duas cores
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
17
Curso Matemática Para Concursos II – Módulo VIII
Evento B: face para o juiz vermelha e face para o jogador amarela, tendo
saído o cartão de duas cores.
Temos:
( A) , isto é, P ( A ∩ B ) = 13 ⋅ 12
P ( A ∩ B ) = P ( A) ⋅ P B
P ( A ∩ B) =
1
(alternativa e)
6
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
18
Curso Matemática Para Concursos II – Módulo VIII
Exercícios Resolvidos
1) Sorteando um número de 1 a 30, qual a probabilidade de que ele seja
par ou múltiplo de 5?
Solução: Seja A (número par)
B (múltiplo de 5)
A = {2; 4;6;...30} → n ( A ) = 15
B = {5;10;15; 20; 25;30} → n ( B ) = 6
A ∩ B = {10; 20;30} → n ( A ∩ B ) = 3
n ( ∪ ) = 30 , temos então:
P ( A ∪ B ) = P ( A) + P ( B ) − P ( A ∩ B )
15 6
3
+ −
=
30 30 30
15 + 6 − 3 18 3
=
=
=
30
30 5
P ( A ∪ B) =
2)
Lançando-se
simultaneamente
dois
dados
não
viciados,
a
probabilidade de que suas faces superiores exibam soma igual a 7 ou 9 é:
a)
1
6
b)
4
9
c)
2
11
d)
5
18
e) n.r.a.
Solução: Temos:
∪ = {(1,1) , (1, 2 ) ,... ( 6,5 ) , ( 6, 6 )} , n ( ∪ ) = 36
Para a soma igual a 7, temos:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
19
Curso Matemática Para Concursos II – Módulo VIII
A = {(1; 6 ) ; ( 2;5 ) ; ( 3; 4 ) ; ( 4;3) ; ( 5; 2 ) ; ( 6;1)}
n ( A) = 6
Para a soma igual a 9, temos:
B = {( 3;6 ) ; ( 4;5 ) ; ( 5; 4 ) ; ( 6;3)}
n ( B) = 4
Como A ∩ B = ∅
P ( A ∪ B) =
6
4 10
5
+
=
=
→ alternativa d.
36 36 36 18
3) Numa pesquisa feita com 600 pessoas de uma comunidade, verificouse que 200 lêem o jornal A, 300 lêem o jornal B e 150 lêem os jornais A e
B. Qual a probabilidade de, sorteando-se uma pessoa, ela ser leitora do
jornal A ou jornal B?
Solução:
n (U ) = 600
n ( A ) = 200
n ( B ) = 300
n ( A ∩ B ) = 150
P ( A ∪ B) =
200 600 150
+
−
→
600 600 600
200 + 300 − 150 350
=
600
600
7
P ( A ∪ B) =
12
P ( A ∪ B) =
4) Extrai-se aleatoriamente uma carta de um baralho de 52 cartas. Qual é
a probabilidade de a carta extraída ser valete ou carta de paus?
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
20
Curso Matemática Para Concursos II – Módulo VIII
Solução:
Seja A o evento “ocorrência de valete”.
n ( A ) = 4 , porque são 4 os valetes.
Seja B o evento “ocorrência de carta de paus”.
n ( B ) = 13 , porque são 13 as cartas de paus.
Como só existe um valete de paus, n ( A ∪ B ) = 1 .
P ( A ∪ B) =
4 13 1 4 + 13 − 1
+ −
=
52 52 52
52
P ( A ∪ B) =
16
4
=
52 13
5) Numa urna há 40 bolas brancas, 25 bolas pretas e 15 vermelhas, todas
de mesmo formato e indistinguíveis pelo tato. Retirando-se uma bola ao
acaso, determine a probabilidade de que ela seja preta ou vermelha.
Solução:
n (U ) = 40 + 25 + 15 = 80
n ( B ) = 40
n ( P ) = 25
n (V ) = 15
n ( P ∩V ) = ∅
P ( P ∪ V ) = P ( P ) + P (V ) − P ( P ∩ V )
25 15 0
+ −
80 80 80
40 1
P ( P ∪V ) =
= = 50%
80 2
P ( P ∪V ) =
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
21
Curso Matemática Para Concursos II – Módulo VIII
Exercícios
1) Um dado é lançado e observa-se o número de face de uma
Ω = {1, 2,3, 4,5, 6}
Ω = espaço amostral
Eis alguns eventos:
A = ocorrência de número ímpar.
Solução:
A = {1,3,5}
B = ocorrência de número primo.
Solução:
B = {2,3,5}
C = ocorrência de número menor que 4.
Solução:
C = {1, 2,3}
D = ocorrência de número menor que 7.
Solução:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
22
Curso Matemática Para Concursos II – Módulo VIII
D = {1, 2,3, 4,5, 6}
E = ocorrência de número maior que 7.
Solução:
E ={
}
ou E = ∅ evento impossível.
2) Dar um espaço amostral para cada um dos experimentos abaixo:
a) Uma urna contém 5 bolas vermelhas (V ) e 2 brancas ( B ) . Duas bolas
são extraídas, sem reposição, e observadas suas cores, na seqüência
que foram extraídas.
Solução:
5V
2B
Ω = {(V , B ) , (V ,V ) , ( B, B ) , ( B,V )}
4 possibilidades
b) Três pessoas A, B, C são colocadas numa fila e observa-se a
disposição das mesmas.
Solução:
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
23
Curso Matemática Para Concursos II – Módulo VIII
Ω = {( A, B, C ) , ( B, C , A) , ( C , B, A ) , ( C , A, B ) , ( B, A, C ) , ( A, C , B )}
c) Um casal planeja ter 3 filhos. Observa-se a seqüência de sexos dos 3
filhos:
Solução:
( M , F , M ) , ( M , F , F ) , ( M , M , F ) , ( M , M , M , ) 
Ω=

( F , F , M ) , ( F , F , F ) , ( F , M , F ) , ( F , M , M ) 
3) No lançamento de um dado, determine a probabilidade de se obter:
a) o número 3
b) um número par
c) um número maior que 2
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
24
Curso Matemática Para Concursos II – Módulo VIII
Solução:
Sendo u = {1; 2;3; 4;5; 6} e n ( u ) = 6 , então:
a) A = {3}
P ( A) =
n ( A) = 1
1
6
b) AΙ = {2, 4, 6}
n ( AΙ ) = 3
P(A ) =
Ι
P ( AΙ ) =
n ( AΙ )
n (u )
3 1
=
6 2
c) AΙΙ = {3; 4;5; 6}
n ( AΙΙ ) = 4
P(A
ΙΙ
n ( AΙΙ )
) = n (u )
=
4 2
=
6 3
4) Considere o experimento aleatório: “Lançar dois dados e obter as faces
voltadas para cima”. Determine a probabilidade de se obter:
a) A soma dos pontos igual a 10;
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
25
Curso Matemática Para Concursos II – Módulo VIII
b) O número em uma das faces igual ao dobro do número na outra face;
c) A soma dos pontos igual a 13;
d) A soma dos pontos menor ou igual a 12;
e) Sair faces iguais.
Solução:
Usaremos
u = espaço amostral
P ( A) → probabilidade de A
(1;1) , (1; 2 ) , (1;3) , (1; 4 ) , (1;5 ) , (1;6 ) , 


( 2;1) , ( 2; 2 ) , ( 2;3) , ( 2; 4 ) , ( 2;5 ) , ( 2; 6 ) , 
 3;1 , 3; 2 , 3;3 , 3; 4 , 3;5 , 3;6 , 
( ) ( ) ( ) ( ) ( ) ( ) 
u=

( 4;1) , ( 4; 2 ) , ( 4;3) , ( 4; 4 ) , ( 4;5 ) , ( 4; 6 ) , 
 5;1 , 5; 2 , 5;3 , 5; 4 , 5;5 , 5;6 , 
( ) ( ) ( ) ( ) ( ) ( ) 
( 6;1) , ( 6; 2 ) , ( 6;3) , ( 6; 4 ) , ( 6;5 ) , ( 6;6 ) 


Temos n ( u ) = 36
a) A soma dos pontos igual a 10
temos: A = {( 4; 6 ) , ( 5;5 ) , ( 6; 4 )} e n ( A ) = 3 , então:
P ( A) =
n ( A)
n (u )
=
3
1
=
36 12
b) A1 ; obter em uma das faces número igual ao dobro do número na outra
face.
A1 = {(1; 2 ) , ( 2;1) , ( 2; 4 ) , ( 3; 6 ) , ( 4; 2 ) , ( 6;3)}
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
26
Curso Matemática Para Concursos II – Módulo VIII
n ( A1 ) = 6 , então:
P ( A1 ) =
n ( A1 )
n (u )
=
6
1
=
36 6
c) A2 : obter soma dos pontos igual a 13, temos A2 = ∅ , então P ( A2 ) = 0
(evento impossível).
d) A3 = u = n ( u ) , então, P ( A3 ) =
36
=1
36
Portanto, P ( A3 ) → evento certo
e) A4 = {(1;1) , ( 2; 2 ) , ( 3;3) , ( 4; 4 ) , ( 5;5 ) , ( 6;6 )}
n ( A4 ) = 6
P ( A4 ) =
6
36
P ( A4 ) =
1
6
5) No jogo da sena seis números distintos são sorteados dentre os
números 1;2;...;50. A probabilidade de que, numa extração, os seis
números sorteados sejam ímpares, vale aproximadamente:
Solução:
O número de elementos do evento é uma combinação de 25 algarismos
ímpares tomados 6 a 6.
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
27
Curso Matemática Para Concursos II – Módulo VIII
n ( E ) = C25,6
O espaço amostral é o número de extrações ou seja, uma combinação de
50 algarismos formados 6 a 6.
P(E) =
P(E) =
n(E)
n (u )
C25,6
C50,6
25!
= 6!19! = 0, 011 ou 1,1%
50!
6!44!
6) Na escolha de um número de 1 a 25, qual a probabilidade de que seja
sorteado um número múltiplo de 6?
Solução:
u = {1; 2;...; 25}
E = {6;12;18; 24}
P(E) =
P(E) =
n(E)
n (u )
4
25
7) Numa empresa, trabalham 10 homens e 5 mulheres. Para formar uma
comissão com 4 pessoa, é feito um sorteio. Qual a probabilidade de se
obter a comissão formada por 2 homens e 2 mulheres?
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
28
Curso Matemática Para Concursos II – Módulo VIII
Solução:
n ( E ) = C10,2 ⋅ C5,2
n ( u ) = C15,4
P(E) =
C10,2 ⋅ C5,2
C5,4
10!
5!
⋅
2!(10 − 2 ) ! 2!( 5 − 2 ) !
P(E) =
15!
4!(15 − 4 ) !
P(E) =
450 30
=
1365 91
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.
29
Curso Matemática Para Concursos II – Módulo VIII
LEMBRETE: Todos os módulos do curso são revisados pela equipe www.somaticaeducar.com.br,
quaisquer divergência com sinais, números, símbolos, soluções dos exercícios, problemas de digitação
ou outros problemas, a www.somaticaeducar.com.br deverá ser comunicada imediatamente para que
sejam resolvidos tais problemas.