3.2 Os dados de um teste tensão-deformação de uma cerâmica são

Resistência dos Materiais
Exercícios de Diagrama Tensão × Deformação
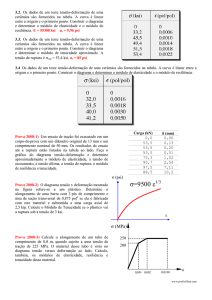
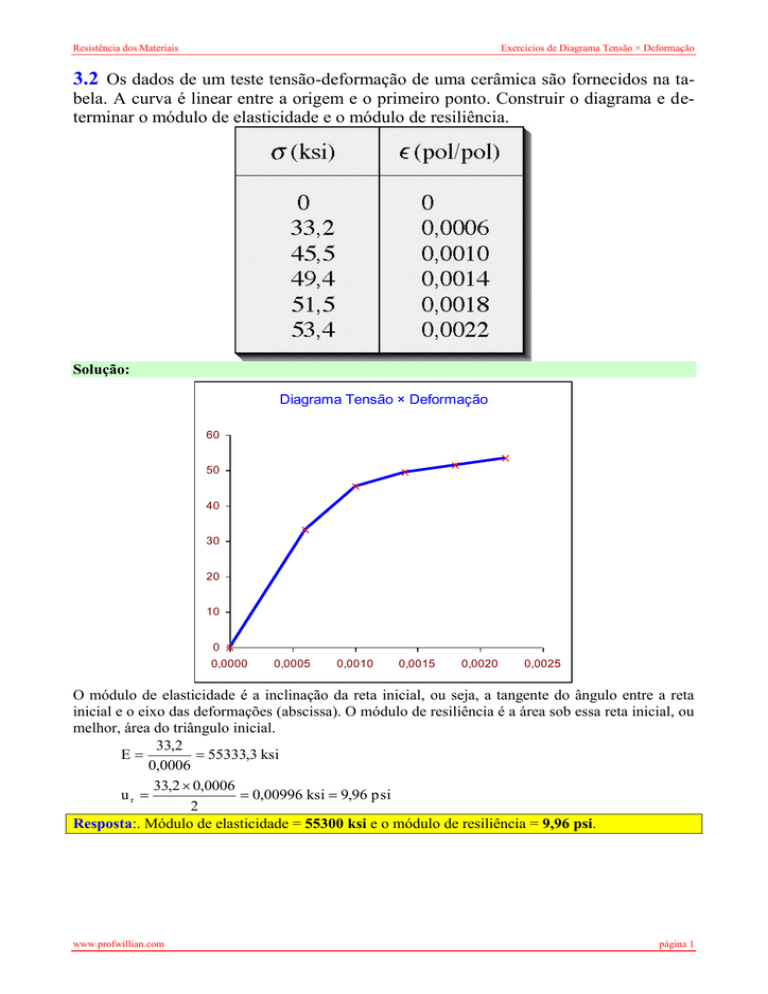
3.2 Os dados de um teste tensão-deformação de uma cerâmica são fornecidos na tabela. A curva é linear entre a origem e o primeiro ponto. Construir o diagrama e determinar o módulo de elasticidade e o módulo de resiliência.
Solução:
Diagrama Tensão × Deformação
60
50
40
30
20
10
0
0,0000
0,0005
0,0010
0,0015
0,0020
0,0025
O módulo de elasticidade é a inclinação da reta inicial, ou seja, a tangente do ângulo entre a reta
inicial e o eixo das deformações (abscissa). O módulo de resiliência é a área sob essa reta inicial, ou
melhor, área do triângulo inicial.
33,2
E
 55333,3 ksi
0,0006
33,2  0,0006
ur 
 0,00996 ksi  9,96 psi
2
Resposta:. Módulo de elasticidade = 55300 ksi e o módulo de resiliência = 9,96 psi.
www.profwillian.com
página 1
Resistência dos Materiais
Exercícios de Diagrama Tensão × Deformação
3.3 Os dados de um teste tensão-deformação de uma cerâmica são fornecidos na tabela. A curva é linear entre a origem e o primeiro ponto. Construir o diagrama e determinar o módulo de tenacidade aproximado se a tensão de ruptura for de 53,4 ksi.
Solução:
Diagrama Tensão × Deformação
60
50
40
30
20
10
0
0,0000
0,0005
0,0010
0,0015
0,0020
0,0025
O módulo de tenacidade será a soma das áreas abaixo da curva do diagrama tensão versus deformação, neste caso, um triângulo e quatro trapézios:
33,2  0,0006 0,0004
0,0004
ut 

 (33,2  45,5) 
 (45,5  49,4) 
2
2
2
0,0004
0,0004
 (49,4  51,5) 
 (51,5  53,4)  0,08584 ksi  85,84 psi
2
2
Resposta:. O módulo de tenacidade = 85,8 psi.
www.profwillian.com
página 2
Resistência dos Materiais
Exercícios de Diagrama Tensão × Deformação
3.4 Os dados de um teste tensão-deformação de uma cerâmica são fornecidos na tabela. A curva é linear entre a origem e o primeiro ponto. Construir o diagrama e determinar o módulo de elasticidade e o módulo de resiliência.
Solução:
Diagrama Tensão × Deformação
45
40
35
30
25
20
15
10
5
0
0,0000
0,0010
0,0020
0,0030
0,0040
0,0050
0,0060
O módulo de elasticidade é a tangente do ângulo entre a reta inicial e o eixo das deformações (abscissa). O módulo de resiliência é a área sob essa reta inicial.
32
E
 20000 ksi
0,0016
32  0,0016
ur 
 0,0256 ksi  25,6 psi
2
Resposta:. O Módulo de elasticidade = 20,0×103 ksi, e o módulo de resiliência = 25,6 psi.
www.profwillian.com
página 3
Resistência dos Materiais
Exercícios de Diagrama Tensão × Deformação
2008-1) Um ensaio de tração foi executado em um corpo-de-prova com um diâmetro original de 13mm e um comprimento nominal de 50mm. Os resultados do ensaio
até a ruptura estão listados na tabela ao lado. Faça o gráfico do diagrama tensãodeformação e determine aproximadamente o módulo de elasticidade, a tensão de escoamento, a tensão última, a tensão de ruptura, o módulo de resiliência e tenacidade.
Carga (kN)
0,0
53,5
53,5
53,5
75,3
90,7
97,5
88,5
(mm)
0,00
0,13
0,20
0,51
1,02
2,54
7,11
10,2
Solução:
A coluna da carga (1 kN = 1000 N) deve ser dividida pela área da seção transversal do corpo-deprova:
  (13mm) 2
A
 132,7323 mm 2
4
A coluna do alongamento 
Tensão x Deformação
deve ser dividida pelo comprimento nominal do corpo-de- 800
prova:
700
L i  50 mm
600
Assim temos uma nova tabela:
 (mm/mm)  (MPa)
0,0000
0,0026
0,0040
0,0102
0,0204
0,0508
0,1422
0,2040
0,0
403,1
403,1
403,1
567,3
683,3
734,6
666,8
500
400
300
200
100
0
0,0000
0,0500
0,1000
0,1500
0,2000
Módulo de Elasticidade E:
403,1 MPa
E
 155026 MPa  155 GPa
0,0026
Módulo de Resiliência ur:
0,0026  403,1 MPa
ur 
 0,524 MPa  524 kPa
2
Utilizando-se a regra dos trapézios (soma de trapézios sob a curva tensão x deformação) temos o
Módulo de Tenacidade: u t  135,6 MPa
Resposta:
Módulo de Elasticidade =
Módulo de Resiliência =
Módulo de Tenacidade =
www.profwillian.com
155 GPa
524 kPa
136 MPa
Tensão de Escoamento =
Tensão Última (Max) =
Tensão de Ruptura =
403 MPa
735 MPa
667 MPa
página 4
Resistência dos Materiais
Exercícios de Diagrama Tensão × Deformação
2008-2) O diagrama tensão x deformação mostrado na figura refere-se a um plástico. Determine o alongamento de uma barra com 3 pés de comprimento e área de seção transversal de 0,875 pol2 se ela é fabricada com este material e submetida a uma
carga axial de 2,5 kip. Calcule o Módulo de Tenacidade se o plástico vai a ruptura
sob a tensão de 3 ksi.
σ (psi)
=9500 1/3
ε
Solução:
  
  

 

 9500 
 9500 
3
  9500 
1/ 3
3
Mas,

P 2500 lbf

 2857,143 psi
A 0,875 in 2
Então:
3
 2857,143 

  0,027204
 9500 
Como:


   L
L
Onde L = 3 pés = 36 pol
Assim,
  0,027204  36
   0,979 pol
Módulo de Tenacidade
3
 rup
 3000 

  0,0314915
 9500 
 rup
ut 
 9500 d  9500
1/ 3
0
4/3
 rup
 9500
4/3
 rup
4/3
4/3
 9500
(0,0314915) 4 / 3
4/3
 70,9 psi
0
Resposta: O alongamento da barra com 3 pés (36 pol) de comprimento será de 0,979 pol e o módulo de tenacidade = 70,9 psi.
www.profwillian.com
página 5
Resistência dos Materiais
Exercícios de Diagrama Tensão × Deformação
2008-3) Calcule o alongamento de um tubo de comprimento de 8,0 m, quando sujeito a uma tensão de tração de 225 MPa. O material desse tubo é visto no diagrama tensão versus deformação ao
lado. Calcule, também, os módulos de elasticidade, resiliência e tenacidade desse material.
 (MPa)
250
200
0,001
0,002
0,0100

Solução:
Módulo de Elasticidade
200
E  tg  
 200000 MPa  200 GPa
0,001
Módulo de Resiliência
0,001  200
ur 
 0,1 MPa
2
Módulo de Tenacidade
0,001 200 (0,002  0,001)
ut 

 200  250  (0,010  0,002)  250  2,325 MPa
2
2
Para uma tensão de 225 MPa temos uma deformação =0,0015, como visto no diagrama. Assim:

       L  0,0015  8000 mm
L
   12 mm
Resposta: O alongamento do tubo de 8000 mm é de 12 mm. Os Módulos de Elasticidade, Resiliência e Tenacidade são: 200 GPa, 100 kPa e 2,33 MPa, respectivamente.
www.profwillian.com
página 6