Relação entre Tensão e Deformação

Relação entre Tensão e Deformação
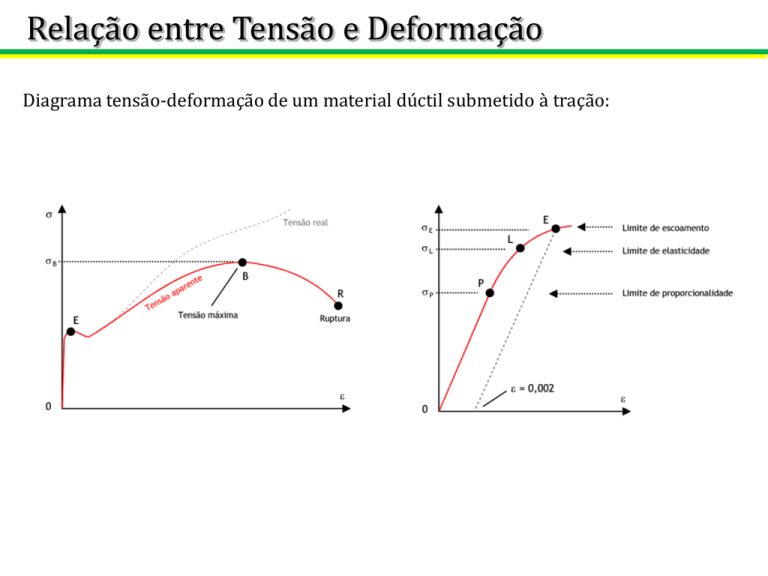
Diagrama tensão-deformação de um material dúctil submetido à tração:
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
1
Relação entre Tensão e Deformação
A relação linear entre a tensão e a deformação é dada por:
σ ij  Cijkl  kl
Para um problema tridimensional, temos:
σ i  Cij  j  i, j  1...6
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
2
Relação entre Tensão e Deformação
A matriz C é denominada de elasticidade, e é dada por:
 c11
c
 12
c23
Cij   
 c14
 c15

 c16
c12
c22
c23
c24
c25
c26
c13
c23
c33
c34
c35
c36
c14
c24
c34
c44
c45
c46
c15
c25
c35
c45
c55
c56
c16 
c26 
c36 

c46 
c56 

c66 
A matriz C é simétrica e tem 21 constantes independentes, e descreve os materiais
Anisotrópicos.
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
3
Relação entre Tensão e Deformação
Material Ortotrópico tem 9 constantes independentes (material compósito, osso,
madeira ...):
 c11
c
 12
c23
Cij   
0
0

 0
c12
c22
c13
0
0
0
c13
c23
c33
0
0
0
0
0
0
c44
0
0
0
0
0
0
c55
0
0
0 
0

0
0

c66 
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
4
Relação entre Tensão e Deformação
Material Ortotrópico (transversalmente isotrópicos):
 c11 c12 c13
c
 12 c11 c13
 c13 c13 c33
Cij    0 0 0

0 0 0

0 0 0

0
0
0
c44
0
0
0
0
0
c44
0
0








 c11  c12  
2
0
0
0
0
0
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
5
Relação entre Tensão e Deformação
Para materiais isotrópicos a matriz de elasticidade é dada por:
 xx 
1
  1
 yy    
  E  
 zz 


1

   xx 
 
   yy 
1   zz 

   xx 
 xx 
1 
E
 
 


 1     yy 
 yy  

  1  1  2   
 


1


 zz 

  zz 
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
6
Relação entre Tensão e Deformação
Para materiais isotrópicos a matriz de elasticidade é dada por:


1 
 
1 

 xx 

 
 
 1 
yy
 

 zz 
E
 0
0
0
 


1


1

2




xy
 

  yz 
 0
0
0
 


 xz 

0
0
 0


E
  G 
G
2 1  
0
0
0
0
0
0
1

2
0
0
1

2
0
0


  xx 
  
  yy 
0   zz 
  
  xy 
0   yz 
 
  xz 
1
 
2

11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
0
0
0
7
Relação entre Tensão e Deformação
Para materiais isotrópicos a matriz de elasticidade é dada por:
1
 xx 
 
 

 yy 
 zz  1  
  
 xy  E  0
0
 yz 

 
 0
 xz 

1

0
0
0


1
0
0
0
0
0
0   xx 
0
0
0   yy 
 
0
0
0   zz 
 
2 1  
0
0    xy 
0
2 1  
0    yz 
 
0
0
2 1      xz 

E
  G 
G
2 1  
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
8
Relação entre Tensão e Deformação
Para as tensões no plano, temos dois modelos:
 Estado plano de tensões mecânicas (EPTM);
 Estado plano de deformações mecânicas (EPDM).
 zz   yz   xz  0
 zz   yz   xz  0 e u2  0
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
9
Relação entre Tensão e Deformação
Estado plano de tensões mecânicas (EPTM) consideramos:
1
 xx 
 
 
yy

 
 zz  1  
  
 xy  E  0
0
 yz 

 

 xz 
 0

1

0
0
0


1
0
0
0
0
0
0   xx 
0
0
0   yy 
 
0
0
0   zz 
 
2 1  
0
0    xy 
0
2 1  
0    yz 
 
0
0
2 1      xz 
 xx 
1
  1
 yy    
  E  0

 xy 

1
0
0   xx 
 
0   yy 
2 1      xy 


1 
 xx 
0   xx 
 
E 
 
 1
0   yy 
 yy  
2 
  
   1   
1


   xy 
 xy 
0 0 


2
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
10
Relação entre Tensão e Deformação
Estado plano de deformações mecânicas (EPDM) consideramos:


1 
 
1 

 xx 

 
 
 1 
 yy 

E
 0
 zz 
0
0
 


 xy  1  1  2  
  yz 
 0
0
0
 

  xz 

0
0
 0

0
0
0
0
0
0
1

2
0
0
1

2
0
0


  xx 
  
  yy 
0   zz 
  
  xy 
0   yz 
 
  xz 
1
 
2

0
0
0

1 
 xx 


E
 
1 
 yy  
 
1


1

2




 

 xy 
0
 0

 xx 

1  
  1   

1


 yy  

E
 
 0
0
 xy 

0   xx 
 
0   yy 
  xy 
1
   
2

0   xx 
 

0   yy 

2  

 xy 
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
11
Referêncas
 Kim, Nam-Ho & Sankar B.V., Introdução à Análise e ao Projeto em
Elementos Finitos, 2009;
 REDDY, J.N., Energy principles and variational methods in applied
mechanics, Hoboken, EUA: Wiley, c2002. xvi, 591 p. ISBN 9780471179856;
 http://ocw.mit.edu/courses/aeronautics-and-astronautics/16-21techniques-for-structural-analysis-and-design-spring-2005/
11th US NATIONAL CONGRESS ON COMPUTATIONAL MECHANICS
12