Aula 04 - Solução

Aula 04
Assunto:
• Equilíbrio dos sólidos
• Refração
• Gravitação
• Pêndulo simples
1.
• Potência elétrica
• Equações dimensionais
• Estudo dos gases
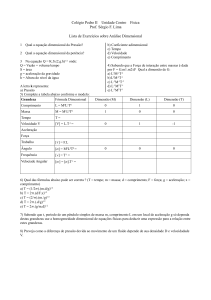
(CEFET/CE-2005) A figura abaixo mostra um operário de peso 900,0N sobre uma prancha de peso 350,0N e comprimento
3,0m. A prancha é articulada na extremidade A e presa na extremidade B a um fio que passa por uma polia. Nessa situação, a
prancha encontra-se em equilíbrio na horizontal e o fio na vertical. Considerando o fio e a polia ideais, determine a tração no
fio e a força de reação na extremidade A da prancha.
Solução:
•
Isolando o operário:
N + T = PH
N = PH — T →
N = 900 — 525
•
Isolando a prancha:
VA + T = PB + N →
VA + 525 = 350 + 375 →
→
N = 375N
VA = 200N
3MAF = 0 → T x 3 — (PH — T) x 2,8 — PB x 1,5 = 0
3T — 2520 + 2,8T — 525 = 0
2.
→
5,8T = 3045
→
T = 525N
(UFGO-2005) Um feixe estreito de luz monocromática, propagando-se inicialmente no ar, penetra em um meio transparente,
formando ângulos de 60° e 30° com a normal, como ilustrado na figura abaixo.
Aula 04
Dados:
Índice de refração do ar = 1,00
Velocidade da luz no ar = 3 x 108m/s
Comprimento de onda da luz no ar = 633nm
Calcule o comprimento de onda da luz no novo meio.
Solução:
NAR . seni = nM . senγ → 1 x
c 3
3
v=
3.
ƒ=
3 c
1
= x
2
v
2
v
→
λ
c
c 3
=
λ AR 3λ M
→
λM =
λ AR 3 633 x
=
3
3
3
λM = 365nm
(UFES-2005) Uma sonda espacial encontra-se em órbita circular em torno de um planeta. Sabe-se apenas que a sonda tem
massa m e a órbita circular tem período T e raio R. Em relação à sonda, determine:
a) o módulo da velocidade;
b) a energia cinética;
c) a energia potencial;
d) a energia mecânica total.
Solução:
a)
v=
b) Ec =
c) EP = —
GMm
→
R
EP = — G
Fc = FG
v 2R
1
.m.
G
R
d) EM = Ec + EP → EM =
4.
→
1 4π 2R 2
m
2
T2
mv 2 GMm
=
R
R2
EP = −
2π2 . R 2 . m
T2
2πR
T
4π 2 . R 2
T2
−
→
Ec =
M=
2mπ 2R 2
T2
v 2R
G
.m
4π 2 . R 2 . m
T2
→
⇒
EM = −
2π2 . R 2m
T2
(UFAL-2005) O corpo suspenso do pêndulo da figura oscila entre os pontos A e B. Iniciando o movimento a partir de A,
contou-se que, em 1 minuto, o corpo suspenso atingiu B e voltou a A, 30 vezes.
a) Calcule o período do pêndulo, em segundos, e o valor de sua freqüência, em hertz.
b) É possível que o comprimento desse pêndulo (L) seja igual a 2,0m? Por quê?
2
OSG 0000/06
Aula 04
Solução:
a) 60s → 30 osc
1s → ƒ → ƒ =
b) T = 2π
5.
L
g
30
60
→
→ T 2 = 4π 2
→
ƒ = 0,5Hz
gt 2
L
→ L=
g
4π2
T=
→ L=
1
ƒ
→
10 x 4
T = 2s
→
4 x π2
L ≅ 1m
(UFES-2005) No circuito mostrado na figura, considere que:
• ε é a f.e.m. da fonte de tensão;
• R1 = R; R2 = 2R e R3 = 3R.
Determine:
a) a corrente que atravessa a fonte de tensão;
b) a corrente que atravessa a resistência R3;
c) a potência dissipada em R2.
Solução:
a) R' =
2R x 3R
2R + 3R
→ R' =
Re = R' + R → Re =
ε = Re . i → ε =
6R
5
11R
6R
+ R → Re =
5
5
11R
. i
5
→
5ε
11R
i=
b) A d.d.p. em R' → V' = R' . i → V' =
A corrente em R3 → V' = R3 . i3 →
c) P2 =
6.
V '2
2R
→ P2 =
36ε 2
1
x
121
2R
5ε
6R
.
11R
5
∴ V' =
6ε
= 3R . i3 →
11
→
P2 =
6ε
11
i3 =
2ε
11R
18ε 2
121R
(UFRJ-2005) Uma partícula de massa m oscila no eixo OX sob a ação de uma força F = -kx3, na qual k é uma constante
positiva e x é a coordenada da partícula.
Suponha que a amplitude de oscilação seja A e que o período seja dado por T = cmαkβAλ onde c é uma constante adimensional e α,
β e λ são expoentes a serem determinados.
Utilize seus conhecimentos de análise dimensional para calcular os valores de α, β e λ.
3
OSG 0000/06
Aula 04
Solução:
Dimensional da constante k → [ F ] = [ k ] [ x ]3
M. L . T-2 = [ k ] . L3 → [ k ] = M . L-2 T—2
Dimensional do período → [ T ] = [ c ] [ m ]α . [ k ]β . [ A ]λ
T = 1 x Mα . (M. L-2 T-2)β . Lλ → T = Mα + β . Lλ - 2β . T—2β
—2β = 1
λ — 2β = 0
7.
→
β=−
→
1
2
λ = 2β
α+β=0
→
→
α = —β
→
α=
1
2
λ=—1
(UFRRJ-2005) Um conjunto de 3 resistores, uma lâmpada e uma bateria. Veja a figura destes elementos.
a) Represente o circuito que produz a maior corrente possível com o uso de todos os elementos citados.
b) Com o mesmo circuito, calcule a energia consumida pela lâmpada durante 5 minutos de uso.
Solução:
a) Para maior corrente os elementos devem ser associados em paralelo.
b) A potência dissipada é a potência nominal
PL = 10W
4
OSG 0000/06
Aula 04
A energia consumida em 5min = 300s é
U=P.t
8.
⇒
U = 10 x 300
→
U = 3000J
(PUC/RJ-2005) Um gás ideal, inicialmente a uma temperatura de 300K e à pressão atmosférica 1 atm, pode ter seu estado modificado
por diferentes processos. Determine:
a) a temperatura final do gás sabendo que este gás é submetido a um processo isovolumétrico e que sua pressão final é o
dobro da pressão inicial.
b) a temperatura final do gás sabendo que este gás é submetido a um processo isobárico e que o volume final ocupado pelo
gás é 1/3 do volume inicial.
Solução:
a) Pi = 1atm
Ti = 300K
Pi Pƒ
=
Ti Tƒ
Pƒ = 2atm
Tƒ = ?
→
Tƒ = 2Ti
Tƒ = 600K
b) Vi •
Vƒ =
Ti = 300K
Vi Vƒ
=
Ti Tƒ
Vi
3
Tƒ
→
Tƒ = 100K
5
OSG 0000/06