Tensão Normal médial

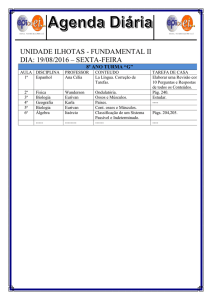
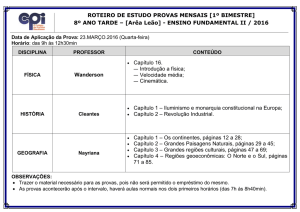
Aula 03 – Tensão; Tensão Normal Média em uma barra com carga axial Prof. Wanderson S. Paris, M.Eng. [email protected] Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Aula 2
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Conceito de Tensão Conceito de
Tensão
Representa
a intensidade
da força
sobre um
plano
•  Representa a intensidade da interna
força interna sobre um plano (área)
específico (área) que passa por um ponto.
específico
que passa
por
um
determinado
determinado ponto. Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais idade da força
ouNormal
força
Tensão por unida
A, é definida
•  A intensidade da como
força ou força tensão
por unidade de normal
área, que atua no sen=do perpendicular a ∆A, é definida como tensão normal, σ (sigma). Portanto pode-­‐ se escrever que: ∆F
σ = lim
∆A→0 ∆A
Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais RESISTÊNCIA DOS MATERIAIS
Tensão Normal AULAS PROF. GILFRAN MILFONT
Carga Axial : Tensão Normal
•  A força resultante interna para um membro carregado axialmente é normal ‡ A tensão
normaltéransversal, definida como: perpendicular ao à seção eixo d
a '
F peça. P
V
V
lim
‡ A força resultante interna para um membro
carregado axialmente é normal à seção
transversal, perpendicular ao eixo da peça.
'Ao 0
'A
med
A
‡ A tensão normal em um ponto pode não ser igual
a tensão normal média, mas a resultante das
tensões na seção precisa satisfazer a equação:
•  O detalhamento da distribuição das tensões em uma determinada seção P V medA ³ dF
³ V dA
não pode ser Adeterminado u=lizando-­‐se ‡ O detalhamento
daa distribuição
das tensões em
somente e
stá=ca. uma determinada seção não pode ser
determinado utilizando-se somente a estática.
Prof. Wanderson S. Paris -­‐ [email protected] 1 - 10
Resistência dos Materiais Aula 2
Unidades de Tensão no SI Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Unidades
de
Tensão
no
SI
•  No Sistema Internacional de Unidades (SI), a intensidade tanto da tensão normal quanto da tensão de cisalhamento é No Sistema Internacional de Unidades (SI), a intensidade tanto da tensão
especificada na unidade básica de newtons por metro normal quanto da tensão de cisalhamento é especificada na unidade básica de
quadrado (N/m2). newtons
por metro
quadrado (N/m²).
• EstaEsta unidade é denominada ascal (1 Pcomo
a = 1essa
N/m2), como unidade
é denominada
pascal (1 Pap=
1 N/m²),
unidade
é
muito
pequena,
nos trabalhos
engenhariansão
prefixos
quilo
essa unidade é muito depequena, os usados
trabalhos de como
engenharia 6) ou giga (109).
(10³),
mega
(10
são usados prefixos como quilo (103), mega (106) ou giga (109). 1MPa = 106 Pa = 106 N / m ²
1GPa = 109 Pa = 109 N / m ²
Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Aula 2
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Tensão N
ormal M
édia
Tensão Normal Média
Hipóteses de simplificação
1) É necessário que a barra permaneça
2) A fim de que a barra
reta tanto antes como depois de a
possa sofrer deformação
carga ser aplicada, e, além disso, a
uniforme, é necessário
seção transversal deve permanecer
que P seja aplicada ao
plana durante a deformação.
longo do eixo do
centróide da seção
transversal e o material
deve ser homogêneo e
isotrópico.
Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Resistência dos Materiais
Tensão Normal Média -­‐ Simplificações •  Material Homogêneo: Possui as mesmas propriedades [sicas e mecânicas em todo o seu volume. •  Material Isotrópico: Possui as mesmas propriedades [sicas e mecânicas em todas as direções. Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Aula 2
Distribuição da Tensão Normal Distribuição da Tensão Normal Média
Média Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
! dF = ! σdA
A
P =σ ⋅ A
σ=
P
A
onde:
σ = Tensão normal média em qualquer ponto da área da
seção transversal.
P = resultante da força normal interna, aplicada no centróide
da área da seção transversal.
A = área da seção transversal da barra.
Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Resistência dos Materiais
Aula 2
Prof. MSc. Luiz Eduardo Miranda J.
Exercício 1
Exercício 1
1) A1)
luminária de 80 kde
g é80
suportada por duas por
hastes AB hastes AB
A luminária
kg é suportada
duas
e BC como mostra a figura. Se AB Se
tem diâmetro de 10 de 10 m
BC
como
mostra
a figura.
AB
tem diâmetro
mm e BC tem diâmetro de 8 mm. Determinar a tensão BC tem diâmetro de 8 mm. Determinar a tensão norma
normal média em cada haste. média em cada haste.
Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Aula 2
Solução do Exercício 1 Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 1
Diagrama de corpo livre:
Determinação das forças em AB e BC:
!F
=0
x
4
FBC ⋅ − FBA ⋅ cos 60° = 0 (I)
5
!F
y
=0
3
FBC ⋅ + FBA ⋅ sen60° − 784,8 = 0 (II)
5
Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Aula 2
Solução do Exercício 1 Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 1
De (I)
4
FBC ⋅ − FBA ⋅ cos 60° = 0
5
5 ⋅ FBA ⋅ cos 60°
(III)
FBC =
4
Substituindo-se (III) em (II), tem-se que:
5
3
⋅ FBA ⋅ cos 60° ⋅ + FBA ⋅ sen60° − 784,8 = 0
4
5
15
⋅ FBA ⋅ cos 60° + FBA ⋅ sen60° − 784,8 = 0
20
& 15
#
FBA ⋅ $ ⋅ cos 60° + sen60° ! − 784,8 = 0
% 20
"
FBA =
784,8
& 15
#
$ ⋅ cos 60° + sen60° !
% 20
"
FBA = 632,38 N
Em (III)
FBC =
5 ⋅ 632,38 ⋅ cos 60°
4
FBC = 395,23 N
Prof. Wanderson S. Paris -­‐ [email protected] Resistência ddos
os MMateriais
ateriais Resistência
Solução do Exercício 1 Aula 2
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 1
Área do Circulo
ACIRC =
π ⋅d2
4
Tensão Normal
σ=
F
F
4⋅ F
=
=
A π ⋅d2 π ⋅d2
4
Cabo BC
σ BC
FBC 4 ⋅ 395,23
=
=
= 7,86 MPa
2
ABC
π ⋅8
Cabo BA
σ BA
FBA 4 ⋅ 632,38
=
=
= 8,05 MPa
2
ABA
π ⋅10
Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Resistência dos Materiais
Exercícios Propostos [P06] Durante uma corrida, o pé de um homem com massa 72 kg é subme=do momentaneamente a uma força equivalente a 5 vezes o seu peso. Determine a tensão normal média desenvolvida na bbia T da perna desse homem na seção média a-­‐a. A seção transversal pode ser considerada circular, com diâmetro externo de 45 mm e diâmetro interno de 25 mm. Considere que a [bula F está suportando nenhuma carga. Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais 20
Exercícios Propostos y Pearson Prentice Hall, Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved. This material is protected under all
. No portion of this material may be reproduced, in any form or by any means, without permission in writing from the publisher.
[P07] O mancal de encosto está sujeito ás cargas mostradas. Determine a tensão normal média desenvolvida nas seções transversais que passam pelos pontos B, C e D. Faça um rascunho dos resultados sobre um elemento de volume infinitesimal localizado em cada seção. Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Exercícios Propostos [P08] O pequeno bloco tem espessura de 5 mm. Se a distribuição de tensão no apoio desenvolvida pela carga variar como mostra a figura, determine a força F aplicada ao bloco e a distância d até o ponto onde ela é aplicada. Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Exercícios Propostos [P09] Omaterial
eixo éis sprotected
ubme=do ucopyright
ma força xial e 40 kN. Determinar a ll rights reserved.
This
underaall
lawsaas
theydcurrently
in any formtensão or by any means,
without
permission
in writing fromqthe
normal média do rolamento ue publisher.
atua sobre o colar C e a tensão normal no eixo. 40 kN.
llar C
40 kN
30 mm
C
40 mm
Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais Exercícios Propostos J. All rights reserved. This material is protected under all copyright laws as they currently
ced, in any form or by any means, without permission in writing from the publisher.
f 5 mm. If[P10] Hastes AB e BC têm cada rmine theuma, um diâmetro de 5 mm. Se uma carga P = 2 kN é aplicada ao anel, determinar a tensão normal média em cada haste se θ = 60 °. 2.309 kN
C
A
u
P
B
C
= 1.155 kN
p
=
(0.005 )
4
2
Prof. Wanderson S. Paris -­‐ [email protected] C are A AB = A BC
Resistência dos Materiais Referências Bibliográficas •  hDp://www.cronosquality.com/aulas/rm/index.html •  Hibbeler, R. C. -­‐ Resistência dos Materiais, 7.ed. São Paulo :Pearson Pren=ce Hall, 2010. •  BEER, F.P. e JOHNSTON, JR., E.R. Resistência dos Materiais, 3.o Ed., Makron Books, 1995. •  Rodrigues, L. E. M. J. Resistência dos Materiais, Ins=tuto Federal de Educação, Ciência e Tecnologia – São Paulo: 2009. •  BUFFONI, S.S.O. Resistência dos Materiais, Universidade Federal Fluminense – Rio de Janeiro: 2008. •  MILFONT, G. Resistência dos Materiais, Universidade de Pernanbuco: 2010. Prof. Wanderson S. Paris -­‐ [email protected] Resistência dos Materiais