Enunciados Abertos e Enunciados Fechados Sumário

Lógica
2014-1
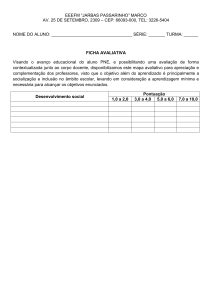
Texto 12
Lógica para Ciência da Computação I
Lógica Matemática
Texto 12
Enunciados Abertos e Enunciados Fechados
Sumário
1 Enunciados atômicos abertos e fechados
1.1 Observações . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Exercı́cios resolvidos . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
3
4
2 Enunciados moleculares abertos e fechados
2.1 Observações . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2 Exercı́cio resolvido . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
7
8
Neste texto, abordamos os conceitos de enunciado aberto e enunciado fechado.
Depois de estudá-lo, vamos ser capazes de:
– determinar quando um enunciado é aberto ou fechado.
1
Lógica
1
2014-1
Texto 12
Enunciados atômicos abertos e fechados
A ocorrência de variáveis em um enunciado pode influenciar fortemente a maneira
como ele é avaliado.
Exemplo 1 Considere os enunciados
2 é positivo
(1)
x é positivo
(2)
e
Sabemos que cada um deles pode ser classificado como V ou F , de maneira exclusiva,
em um dado contexto. Mas há uma diferença bastante sutil entre os contextos nos
quais eles devem ser avaliados.
Para entender esta diferença vamos considerar que ambos os enunciados foram
escritos em um quadro-negro de uma sala de aula, por um professor de Matemática,
que está estudando com seus alunos os números inteiros (negativos, zero e positivos):
. . . , −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, . . .
Após escrever os enunciados no quadro, o professor escolheu um aluno estudioso
e perguntou:
O enunciado (1) é V ou F ?
O aluno estudioso não teve nenhuma dúvida em responder:
O enunciado (1) é V .
Depois de parabenizá-lo pela resposta correta, o professor perguntou ao mesmo
aluno:
E o enunciado (2), ele é V ou F ?
Mesmo sendo estudioso, é certo que ao avaliar o enunciado (2) o aluno teve
dúvidas e, muito provavelmente, o melhor que pode fazer foi devolver para o professor
uma outra pergunta:
Mas professor..., qual é o valor de x?
De fato, o que o aluno perguntou ao professor fazia muito sentido, uma vez que,
se o professor respondesse para ele que o valor de x era −2, o aluno deveria responder
que o enunciado era F , mas se o professor respondesse que o valor de x era 3, o aluno
devereria responder que o enunciado era V .
O Exemplo 1 sugere que, a princı́pio, podemos considerar a existência de dois
tipos de enunciados:
2
Lógica
2014-1
Texto 12
(a) aqueles que, como (1), só possuem ocorrências de constantes e, por esta razão,
podem ser avaliados diretamente, quando conhecemos o contexto no qual eles
são pronunciados;
(b) aqueles que, como (2), possuem ocorrências de ao menos uma variável e, por
esta razão, não podem ser avaliados diretamente, mesmo que conheçamos o
contexto no qual eles são pronunciados.
Baseados nesta distinção, temos a seguinte classificação dos enunciados atômicos:
Seja ϕ um enunciado atômico.
(1) Dizemos que ϕ é fechado se todas as expressões que ocorrem nele são
constantes.
(2) Alternativamente, dizemos que ϕ é aberto se pelo menos uma das expressões
que ocorre nele é uma variável.
Exemplo 2 (a) Os enunciados
Augusto é tutor de MD
Leonardo e Carolina são casados
8.589.869.056 é perfeito
17.296 e 18.416 são amigos
são fechados.
(b) Os enunciados
x é tutor de MD
Leonardo e y são casados
x e Carolina são casados
y e z são casados
m é perfeito
x e 18.416 são amigos
17.296 e y são amigos
x e y são amigos
são abertos.
1.1
Observações
Observação 1 Alguns autores não consideram que enunciados abertos como
ela é professora
,
3
x é um número real
Lógica
2014-1
Texto 12
são enunciados. Eles argumentam que estas frases não podem ser classificadas como
V ou F , pois suas avaliações dependem dos valores das variáveis que ocorrem nelas.
Mas lembremos que, para nós, um enunciado é uma frase que pode ser classificada
como V ou F em um dado contexto e que nos contextos em que conhecemos os
valores das variáveis, frases como estas podem, em princı́pio, ser classificadas como
V ou F , de maneira exclusiva. Assim, consideramos que elas são enunciados.
1.2
Exercı́cios resolvidos
Exercı́cio 1 Determine as constantes e as variáveis que ocorrem em cada um dos
enunciados.
(i)
2 é o menor número primo
(ii) ele é o meu primo mais novo
(iii) 2 e p são primos entre si
(iv) João está em casa
(v) X está entre (0, 1) e (0, 5)
Exercı́cio 2 Classifique cada enunciado do Exercı́cio 1 em aberto ou fechado.
Antes de ler as resoluções, tente resolver os exercı́cios usando os
conceitos estudados.
Resolução do Exercı́cio 1: (i) Constante: 2. Nenhuma variável. (ii) Nenhuma
constante. Variável: ele. Pode ser reescrito como x é meu primo mais novo. (iii)
Constante: 2. Variável: p. (iv) Constante: João. Nenhuma variável. (v) Constantes:
(0, 1) e (0, 5). Variável: X. As constantes (0, 1) e (0, 5) são formadas a partir das
outras constantes, 0, 1 e 5, por meio de uma notação especial.
Resolução do Exercı́cio 2: (i) Fechado, pois é atômico e não possui ocorrência
de variável. (ii) Aberto, pois é atômico e possui ocorrência de variável. (iii) Aberto,
pois é atômico e possui ocorrência de variável. (iv) Fechado, pois é atômico e não
possui ocorrência de variável. (v) Aberto, pois é atômico e possui ocorrência de
variável.
2
Enunciados moleculares abertos e fechados
Com um pouco de cuidado, a classificação em aberto ou fechado se estende de
maneira natural para enunciados moleculares.
Exemplo 3 (a) Os enunciados
Leonardo e Carolina não são namorados
João é inteligente e João é preguiçoso
243112609 − 1 é primo ou 243112609 − 1 é composto
4
Lógica
2014-1
Texto 12
são fechados.
(b) Os enunciados
Se x está noiva, então x usa aliança
y vai ao cinema todas as semanas ou y não é cinéfilo
Se p é primo e p é maior do que 2, então p é ı́mpar
z é primo se, e somente se z 6= 1 e z não possui divisores próprios
são abertos.
Os Exemplos 2 e 3 mostram alguns enunciados atômicos e alguns enunciados
moleculares cuja classificação em abertos ou fechados não apresenta dificuldades.
Nestes exemplos, a classificação dos enunciados como abertos se deve apenas ao fato
de que eles possuem ocorrências de variáveis. Mas, como veremos a partir de agora,
a classificação de um enunciado molecular como aberto ou fechado é um pouco mais
sutil e, geralmente, mais difı́cil do que simplesmente verificar se ele possui ou não a
ocorrência de variáveis.
O principal ponto a ser observado é que enunciados abertos — tanto os atômicos
quanto os moleculares — dão origem a enunciados fechados por dois processos distintos:
– substituição de uma variável por uma constante;
– quantificação de uma variável.
Vamos, agora, exemplificar cada um destes processos. Nestes exemplos, consideramos que os enunciados de conteúdo não matemático se referem a pessoas e que
os enunciados de conteúdo matemático se referem a números naturais não nulos:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, . . .
Sejam ϕ um enunciado, v uma variável que ocorre em ϕ e c uma constante
qualquer.
O processo de substituir v por c em ϕ consiste, simplesmente, em escrever a
constante c nos lugares aonde ocorre a variável v em ϕ.
Este processo, quando aplicado a enunciados atômicos, gera enunciados atômicos;
e, quando aplicado a enunciados moleculares, gera enunciados moleculares.
Exemplo 4 (a) A partir do enunciado aberto
x é professora
podemos formar os enunciados fechados
Eliane é professora
Kátia é professora
Regina é professora
5
Lógica
2014-1
Texto 12
e muitas outras, obtidas a partir do enunciado aberto pela substituição da variável
x
por nomes próprios.
(b) A partir do enunciado aberto
n é par
podemos formar os enunciados fechados
1 é par
2 é par
3 é par
e muitos outros, obtidos a partir do enunciado aberto pela substituição da variável
n
por numerais.
Seja ϕ um enunciado e v uma variável que ocorre em ϕ.
O processo de quantificar v consiste em prefixar ϕ com uma das expressões
para todo v
ou
existe ao menos um v
usualmente, tendo primeiro encerrado ϕ entre parênteses.
Este processo, quando aplicado a enunciados atômicos ou a enunciados moleculares, gera enunciados moleculares.
Exemplo 5 (a) A partir do enunciado atômico aberto
n é par
podemos formar os enunciados moleculares fechados
para todo n (n é par)
existe ao menos um n (n é par)
obtidos a partir do enunciado aberto pela quantificação da variável n.
Observe que estes são os únicos enunciados fechados que podem ser obtidos a
partir do enunciado dado pela quantificação da variável.
6
Lógica
2014-1
Texto 12
A diferença sutil do papel desempenhado por cada variável em enunicados como
a é divisor de 12
para todo a (a é divisor de 12)
existe a (a é divisor de 12)
apresentados no Exemplo 5(a) motiva a seguinte definição:
Seja ϕ um enunciado molecular.
Dizemos que ϕ é fechado se ϕ não possui ocorrências de variáveis ou se todas
as variáveis que ocorrem em ϕ estão quantificadas.
Mais adiante, vamos estudar mais detalhadamente a formação e a avaliação de
proposições que possuem ocorrências de quantificadores.
2.1
Observações
Observação 2 Quando substituı́mos variáveis por constantes, todas as ocorrências
da variável devem ser substiuı́das pela contante.
Por exemplo, substituindo x por −1 no enunciado molecular aberto
x é o simétrico de 1 e x elevado ao quadrado é igual a 1
obtemos o enunciado fechado
−1 é o simétrico de 1 e −1 elevado ao quadrado é igual a 1
Observação 3 Assim como podemos formar enunciados fechados a partir de enunciados abertos pela substituição de variáveis por constantes, também podemos efetuar o processo reverso de substituir constantes por variáveis e formar enunciados
abertos a partir de enunciados fechados.
Por exemplo, substituindo −1 por x no enunciado fechado
−1 é o simétrico de 1 e −1 elevado ao quadrado é igual a 1
voltamos ao enunciado aberto
x é o simétrico de 1 e x elevado ao quadrado é igual a 1
Observação 4 Assim como podemos formar enunciados fechados a partir de enunciados abertos pela quantificação de variáveis, também podemos efetuar o processo
reverso de desquantificar variáveis e formar enunciados abertos a partir de enunciados fechados.
Por exemplo, desquantificando a variável x no enunciado fechado
existe ao menos um x (x é real e x2 − x − 1 = 0)
obtemos o enunciado aberto
x é real e x2 − x − 1 = 0
7
Lógica
2.2
2014-1
Texto 12
Exercı́cio resolvido
Exercı́cio 3 Classificar cada enunciado abaixo como aberto ou fechado.
√
(i)
2 é racional
(ii) M é uma matriz quadrada
(iii) x2 + y 2 = z 2
(iv) para todos x, y e z: x2 + y 2 = z 2
(v) existem x e y tais que: x3 + y 3 = z 3
Antes de ler a resolução, tente resolver o exercı́cio usando os conceitos estudados.
Resolução do Exercı́cio 3: (i) Fechado, pois é atômico e não possui ocorrência
de variável. (ii) Aberto, pois é atômico e possui ocorrência de variável. (iii) Aberto,
pois é atômico e possui ocorrência de variável. (iv) Fechado, pois todas as ocorrências
de variáveis estão quantificadas. Pode ser reescrito como para todo x, para todo y
e para todo z: x2 + y 2 = z 2 . (v) Aberto, pois a ocorrência da variável z não está
quantificada. Pelo processo de quantificação da variável z, este enunciado dá origem
a dois outros enunciados fechados: existe x, existe y e existe z tais que: x3 + y 3 = z 3
e existe x e existe y tais que para todo z: x3 + y 3 = z 3 .
c 2014 Márcia Cerioli, Renata de Freitas e Petrucio Viana
IM-UFRJ, IME-UFF
8