Aula 3 - Tensão Admissível, Fator de Segurança e Projeto de

Resistência dos Materiais
Aula 3 – Tensão Admissível, Fator
de Segurança e Projeto de
Acoplamentos Simples
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Tópicos Abordados Nesta Aula
Tensão Admissível.
Fator de Segurança.
Projeto de Acoplamentos Simples.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Tensão Admissível
O engenheiro responsável
pelo projeto de elementos
estruturais ou mecânicos
deve restringir a tensão do
material a um nível seguro,
portanto, deve usar uma
tensão segura ou admissível.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Fator de Segurança (F.S.)
O fator de segurança (F.S.) é a relação entre a carga de
ruptura Frup e a carga admissível Fadm.
O fator de segurança é um número maior que 1 a fim de
evitar maior possibilidade de falha.
Valores específicos dependem dos tipos de materiais usados
e da finalidade pretendida da estrutura ou máquina.
F .S . =
Frup
Fadm
σ rup
F .S . =
σ adm
τ rup
F .S . =
τ adm
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Projeto de Acoplamentos Simples
Elemento sujeito a aplicação de
força normal:
A=
Elemento sujeito a aplicação de
força de cisalhamento:
P
A=
σ adm
P
τ adm
Problemas comuns:
1) Área da seção transversal de um elemento de tração.
2) Área da seção transversal de um acoplamento submetido a cisalhamento.
3) Área requerida para resistir ao apoio.
4) Área requerida para resistir ao cisalhamento provocado por carga axial.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Área da Seção Transversal de um Elemento
sob Tração
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Acoplamento Submetido a Cisalhamento
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Área Requerida para Apoio
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Cisalhamento por Carga Axial
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Exercício 1
1) O tirante está apoiado em sua extremidade por um disco circular fixo como
mostrado na figura. Se a haste passa por um furo de 40 mm de diâmetro, determinar
o diâmetro mínimo requerido da haste e a espessura mínima do disco necessários
para suportar uma carga de 20 kN. A tensão normal admissível da haste é σadm = 60
MPa, e a tensão de cisalhamento admissível do disco é τadm = 35 MPa.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 1
Diâmetro da haste: por
verificação, a força axial na
haste é 20 kN, assim, a área
da seção transversal da haste
é dada por:
A=
Sabe-se que:
A=
20000
A=
60
A = 333,33 mm²
4
Portanto:
P
σ adm
π ⋅d2
d=
d=
4⋅ A
π
4 ⋅ 333,33
π
d = 20,60 mm
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 1
A área seccionada é dada por:
A=
V
τ adm
20000
A=
35
A = 571,42 mm²
A = 2 ⋅π ⋅ r ⋅ t
Portanto:
t=
A
2 ⋅π ⋅ r
571,42
t=
2 ⋅ π ⋅ 20
t = 4,55 mm
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Exercício 2
2) A barra rígida mostrada na figura é suportada por uma haste de aço AC
que tem diâmetro de 20 mm e um bloco de alumínio que tem área da seção
transversal de 1800 mm². Os pinos de 18 mm de diâmetro em A e C estão
submetidos a um cisalhamento simples. Se a tensão de ruptura do aço e do
alumínio forem (σaço)rup = 680 MPa e (σal)rup = 70 MPa, respectivamente, e a
tensão de cisalhamento de ruptura de cada pino for τrup = 900 MPa,
determinar a maior carga P que pode ser aplica à barra. Aplicar F.S = 2.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 2
∑M
Diagrama de corpo livre:
A
=0
FB ⋅ 2 − P ⋅ 0,75 = 0
Relação entre as forças:
Reações de apoio:
∑M
B
=0
− FAC ⋅ 2 + P ⋅1,25 = 0
FAC
1,25 ⋅ P
=
2
FAC = 0,625 ⋅ P
0,75 ⋅ P
FB =
2
FB = 0,375 ⋅ P
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 2
Aço
Alumínio
(σ )
aço rup
(σ al )rup
(σ )
=
(σ )
680
=
2
(σ al )adm
(σ )
= 340 MPa
(σ al )adm = 35 MPa
aço adm
aço adm
aço adm
F .S .
(σ al )adm =
Pino
τ adm =
F .S .
70
=
2
τ adm =
τ rup
F .S .
900
2
τ adm = 450 MPa
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 2
Barra AC
(σ )
aço adm
(σ )
aço adm
(σ )
aço adm
(σ )
aço adm
FAC
=
AAC
FAC
=
π ⋅d2
4
4 ⋅ FAC
=
π ⋅d2
=
P=
(σ )
aço
2
⋅
π
⋅
d
adm
4 ⋅ 0,625
340 ⋅ π ⋅ 20 2
P=
4 ⋅ 0,625
P = 170816 N
4 ⋅ 0,625 ⋅ P
π ⋅d2
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 2
Bloco B
(σ al )adm = FB
AB
(σ al )adm
P=
0,375 ⋅ P
=
AB
P=
35⋅1800
0,375
P = 168000 N
(σ al )adm ⋅ AB
0,375
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Solução do Exercício 2
Pino A
τ adm
V
=
Ap
450 ⋅ π ⋅182
P=
4 ⋅ 0,625
V = FAC = τ adm ⋅ Ap
0,625 ⋅ P = τ adm ⋅
P=
π ⋅d2
4
P = 183124 N
Por comparação, a
maior carga que pode
ser aplicada ao sistema é
P = 168000 N, pois
qualquer carga maior
que essa fará com que a
tensão admissível seja
excedida.
τ adm ⋅ π ⋅ d 2
4 ⋅ 0,625
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Exercícios Propostos
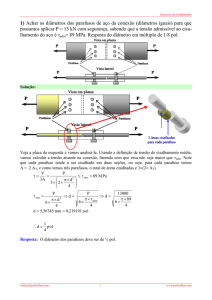
1) Uma carga axial no eixo mostrado na figura é resistida pelo colar em C, que
está preso ao eixo e localizado à direita do mancal em B. Determinar o maior
valor de P para as duas forças axiais em E e F de modo que a tensão no colar
não exceda uma tensão de apoio admissível em C de σadm = 75 MPa e que a
tensão normal média no eixo não exceda um esforço de tração admissível de
σadm = 55 MPa.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Exercícios Propostos
2) A alavanca é presa ao eixo A por meio de uma chaveta que tem largura d e
comprimento de 25 mm. Supondo que o eixo esteja fixo e seja aplica uma força
vertical de 200 N perpendicular ao cabo, determinar a dimensão d se a tensão de
cisalhamento admissível para a chaveta for τadm = 35 MPa.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Exercícios Propostos
3) As duas hastes de alumínio suportam a carga vertical P = 20 kN. Determinar seus
diâmetros requeridos se o esforço de tração admissível para o alumínio for (σt)adm = 150
MPa.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Exercícios Propostos
4) O punção circular B exerce uma força de 2 kN no topo da chapa A. Determinar a tensão
de cisalhamento média na chapa devida a esse carregamento.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Exercícios Propostos
5) O conjunto da correia sobreposta será submetido a uma força de 800 N. Determinar (a)
a espessura t necessária para a correia se o esforço de tração admissível para o material for
(σt)adm = 10 MPa, (b) o comprimento dl necessário para a sobreposição se a cola pode
resistir a um esforço de cisalhamento admissível de (τadm)c = 0,75 MPa e (c) o diâmetro dr
do pino se a tensão de cisalhamento admissível para o pino for (τadm)p = 30 MPa.
Resistência dos Materiais
Aula 3
Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
Próxima Aula
Estudo de Deformações, Normal e por
Cisalhamento.
Propriedades Mecânicas dos Materiais.
Coeficiente de Poisson.
Resistência dos Materiais