do arquivo

PROF. GUSTAVO VIEGAS
MATEMÁTICA
RESUMO TEÓRICO
Geometria Analítica
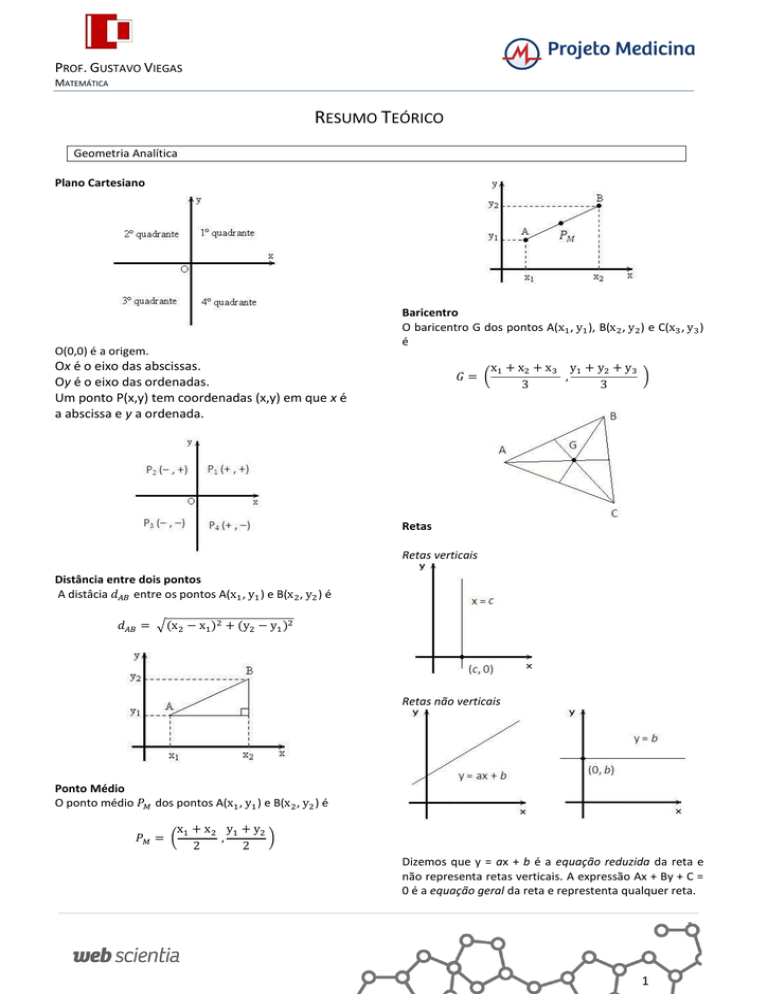
Plano Cartesiano
Baricentro
O baricentro G dos pontos A( ,
é
O(0,0) é a origem.
Ox é o eixo das abscissas.
Oy é o eixo das ordenadas.
Um ponto P(x,y) tem coordenadas (x,y) em que x é
a abscissa e y a ordenada.
(
), B( ,
) e C( ,
)
)
Retas
Retas verticais
Distância entre dois pontos
A distâcia
entre os pontos A( ,
√(
)
) e B( ,
(
)é
)
Retas não verticais
Ponto Médio
O ponto médio
dos pontos A( ,
(
) e B( ,
)é
)
Dizemos que y = ax + b é a equação reduzida da reta e
não representa retas verticais. A expressão Ax + By + C =
0 é a equação geral da reta e represtenta qualquer reta.
1
PROF. GUSTAVO VIEGAS
MATEMÁTICA
Equação da reta
Área do triângulo
a) Reta que passa por dois pontos
Sejam
. Para encontrar a equação da reta y = ax +
b que passa por ( , ) e ( , ), basta resolver o
sistema
A área do triângulo de vértices A( ,
C( , ) é
{
||
), B( ,
) e
||
Note que se a A = 0, então os pontos estão alinhados.
Se ( , ) e ( , ) pertencem à reta com
, então a reta é vertical e sua equação é x =
e
.
Equação da circunferência
b) reta que passa por um ponto e a declividade é
conhecida.
Sejam P(x, y) um ponto genérico, ( , ) um ponto
fixado e a a declividade da reta. Então
y – = a(x – )
A equação da circunferência de raio r e centro C(
(
)
(
)
,
)é
Retas paralelas e retas percendiculares
Dada a reta y = ax + b, a declividade vale
Se y =
x +
e y =
x +
são paralelas, então
.
Se y =
x+
.
ey=
x+
são perdiculares, então
Observação
Para verificar se A + B + Cxy + Dx + Ey + F = 0
representa uma circunferência, completamos os
quadrados. Como, necessariamente, A = B e C = 0
A + Dx + A + Ey + F = 0
Distância entre ponto e reta
A distância d entre a reta Ax + By + C = 0 e o ponto
P( , ) é
|
|
+ x+
(
+ y+
) +(
=0
) =
+( ) +( )
√
2