RESOLUÇÃO DA AVALIAÇÃO DE MATEMÁTICA 1a SÉRIE DO

RESOLUÇÃO DA AVALIAÇÃO DE MATEMÁTICA
1a SÉRIE DO ENSINO MÉDIO – 15/08/09
PROFESSOR: ROBERTO CIDREIRA
Sejam: A = {2, 4, 6, 8, 10, 12,.... 62, 64} e B = {(m, n) ∈ A x A | m + n = 64}.
O número de elementos de B é igual a:
A
A
Sabendo que n(A) = 32, e que é possível formar pares ordenados
2
4
6
8
.
.
.
60
62
64
2
4
6
8
.
.
.
60
62
64
(x; y) ∈ A X A tais que x + y = 64, conclui-se que somente os pares
ordenados (64; y) e (x; 64) não poderão ser formados pois o
conjunto A não possui o elemento zero.
Logo, só é possível formar 31 pares ordenados (x; y) tais que x + y = 64.
veja a sequência!
((2;62); (4;60); (6;58);...; (60;4); (62;2))
Para todos os pares ordenados de números inteiros define-se uma operação ∆ por: (a; b) ∆ (c; d) = (a + c;
b – d). Se um par de números inteiros (x; y) é tal que [(1; 2) ∆ (–2; 3)] ∆ (x; y) = (–1; 2), então x + y é
igual a:
1O PASSO
2O PASSO
[(1;2) ∆ (–2;3)] ∆ (x; y) = (–1; 2)
–1 + x = –1 e –1 – y = 2
(1 + (–2); 2 – (3)) ∆ (x; y) = (–1; 2)
x = 0 e –y = 3
(–1; –1) ∆ (x; y) = (–1; 2)
y = –3
(–1 + x; –1 – y) = (–1; 2)
Daí, vem:
x + y = –3
Qual dos seguintes gráficos não representa uma função f : R → R?
Esse gráfico
0
x
Pois existem elementos do domínio com mais de uma imagem ou existem elementos do conjunto
partida sem imagem.
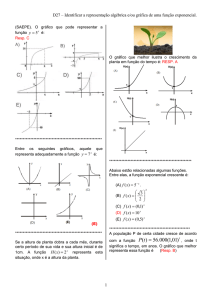
O gráfico de uma função f é:
O domínio e o conjunto imagem de f são respectivamente:
Resp.: [–5, –3[ ∪ [4, 7[ e ]–2, 5].
Justificativa: Interpretação gráfica.
Seja f : R → R tal que y = f(x).
Analisando o gráfico de f, representado acima, assinale a afirmação correta:
Resp.: f(–3) = f(6).
Justificativa: Interpretação gráfica.
O domínio da função y =
1
x +1
−
1
x −1
é:
Resp.: ]1, + ∞[
1o PASSO
2o PASSO
x+1>0
x–1>0
I)
x > –1
x > 1 II
II)
I
I ∩ II
–1
1
1
Sobre a função f, de [a, b] em R, cujo gráfico se vê acima, é verdade que:
Resp.: f(0) ≤ 0 para todo x no intervalo [d, e].
Justificativa: Interpretação gráfica.
Seja uma função y = f(x) cujo gráfico está representado abaixo.
Assinale a afirmação correta:
Resp.: f(x1) = f(x3) = f(x5) = 0.
Justificativa: Interpretação gráfica.
Qual das funções a seguir não possui raiz real?
Resp.: t(x) = x − 1 − x .
Justificativa:
x −1− x = 0
Como o discriminante "∆" da equação é negativo, a
equação não admite raízes reais.
x −1= x
x – 1 = x2
x2 – x + 1 = 0
∆=1–4
∆ = –3
Toda criança é feliz. Algumas pessoas que usam óculos são infelizes. Logo:
Resp.: todas as crianças que usam óculos são felizes.
Numa indústria trabalham 40 homens. As mulheres constituem 31,25% dos trabalhadores e os menores
representam 20% do total de mulheres.
Quantos trabalham nessa indústria?
1o PASSO
3o PASSO
Considere
No DE PESSOAS
PERCENTUAL
40
62,5
x
100
H: conjunto dos homens;
M: conjunto das mulheres;
C: conjunto dos menores.
62,5x = 4000
2o PASSO
x=
n(c) = 20% de n(m)
6,25
4000
62,5
x = 64
20 1
31,25
n(c) =
.
100 5
100
1
n(c) = 6,25%
Logo, n(c) + n(m) ⇔ 37,5%
Daí, vem que n(H) = 62,5%
O gráfico de R x {0, 2} é a figura constituída por:
Resp.: duas retas paralelas a OX .
Justificativa: Representação gráfica abaixo.
y
2
1
0
x
João e José sentam-se, juntos, em um restaurante. O garçom, dirigindo-se a João, pergunta-lhe: “Acaso
a pessoa que o acompanha é seu irmão?” João responde ao garçom: “Sou filho único, e o pai da
pessoa que me acompanha é filho de meu pai”.
Então, José é:
Resp.: filho de João
Considerando o indivíduo "I" como o pai de João, podemos concluir que no momento em que João
responde ao garçom: "Sou filho único, e o pai da pessoa que me acompanha é filho de meu pai",
pode-se concluir que o pai de José é filho de "I", logo José é filho de João.
Durante o tratamento térmico de uma peça metálica, sua temperatura varia de acordo com o gráfico.
É válido afirmar-se:
Resp.: A partir do instante t = 20, as temperaturas são crescentes.
Justificativa: A partir do instante T = 20 a função representada é estritamente crescente.
T(ºC)
20
10
0
100
T(ºX)
Determine a temperatura em graus Celsius associada à temperatura expressa em 200ºX, sabendo que
1
x + 10.
a função T( x ) =
10
T(200) =
1 20
( 200) + 10
10
T(200) = 20 + 10
T(200) = 30
Resp.: 30ºC