A Derivada e a Inclinação de um Gráfico

1. Tangente a um gráfico
UNIVERSIDADE DO ESTADO DE MATO GROSSO
CAMPUS UNIVERSITÁRIO DE SINOP
FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS
CURSO DE ENGENHARIA CIVIL
DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I
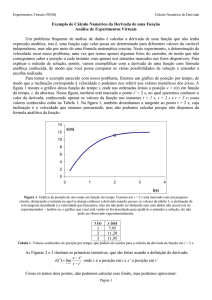
Por exemplo, na figura abaixo, a parábola
sobe mais rapidamente no ponto (x1, y1) do que no
ponto (x2, y2). No vértice (x3, y3), o gráfico deixa
de subir ou descer, e no ponto (x4, y4), o gráfico
está descendo.
A Derivada e a Inclinação de um Gráfico
Prof.: Rogério Dias Dalla Riva
4
A Derivada e a Inclinação de um Gráfico
1. Tangente a um gráfico
1.Tangente a um gráfico
Para determinar a taxa à qual um gráfico
sobe ou desce em um ponto determinado, podemos
achar o coeficiente angular da tangente no ponto.
Em termos simples, a tangente ao gráfico de uma
função f em um ponto P (x, y) é a reta que melhor
aproxima o gráfico naquele ponto, conforme
mostra a figura do slide anterior.
2.Inclinação de um gráfico
3.Inclinação e o processo de limite
4.A derivada de uma função
5.Diferenciabilidade e continuidade
5
1. Tangente a um gráfico
1. Tangente a um gráfico
A figura abaixo ilustra outros exemplos de
tangentes.
O Cálculo é o ramo da matemática que
estuda as taxas de variação de funções. Na função
de 1o grau, sabemos que o coeficiente angular de
uma reta indica a taxa à qual a reta sobe ou desce.
Para uma reta, esta taxa é a mesma em todos os
seus pontos. Para outros gráficos, que não retas, a
taxa à qual o gráfico sobe ou desce pode variar de
ponto para ponto.
3
6
1
1. Tangente a um gráfico
2. Inclinação de um gráfico
Quando Isaac Newton (1642-1727) estava
trabalhando no “problema da tangente”, constatou
quão difícil era definir com precisão o que significa
tangente a uma curva genérica. Pela geometria,
sabemos que uma reta é tangente a um círculo se o
intercepta em apenas um ponto, conforme a figura
abaixo.
Exemplo 1: Utilizando o gráfico abaixo, obtenha
uma aproximação da inclinação do gráfico de
f(x) = x2 no ponto (1, 1).
7
1. Tangente a um gráfico
10
2. Inclinação de um gráfico
As tangentes a gráficos não-circulares,
entretanto, podem interceptar o gráfico em mais
de um ponto. Assim é que, no gráfico da figura
abaixo, se prolongarmos a tangente ela irá
interceptar o gráfico em outro ponto distinto do
ponto de tangência. Veremos como a noção de
limite pode ser usada para definir uma tangente
genérica.
Pelo gráfico de f(x) = x2,
vemos que a tangente em (1, 1)
sobe aproximadamente duas
unidades para cada unidade de
variação em x. Assim, o coeficiente angular da tangente em
(1, 1) é dado por
variação de y 2
= =2
variação de x 1
8
11
2. Inclinação de um gráfico
2. Inclinação de um gráfico
Como a tangente é a aproximação linear do
gráfico em um ponto, o problema da determinação
da inclinação de um gráfico se reduz ao de achar o
coeficiente angular da tangente naquele ponto.
Como a tangente no ponto
(1, 1) tem inclinação 2 aproximadamente, podemos concluir que o
gráfico tem essa mesma inclinação em (1, 1)
9
12
2
2. Inclinação de um gráfico
3. Inclinação e o processo de
limite
Exemplo 2: A figura abaixo ilustra a temperatura
diária (em graus Fahrenheit) em Duluth,
Minnesota. Estime a inclinação deste gráfico no
ponto indicado e interprete fisicamente o
resultado.
Se (x, f(x)) é o ponto de tangência e
(x + ∆x, f(x + ∆x)) é um segundo ponto do gráfico
de f, então o coeficiente angular da secante pelos
dois pontos é
13
msec =
f ( x + ∆x ) − f ( x ) ∆y
=
∆x
∆x
Coef. ang. da secante
16
3. Inclinação e o processo de
limite
2. Inclinação de um gráfico
Pelo gráfico podemos
ver que a tangente no ponto
dado cai aproximadamente 27
unidades para cada duas
unidades de variação de x.
Podemos, assim, estimar a
inclinação no ponto dado
como
variação de y −27
=
= −13,5 graus/mês.
variação de x
2
O membro direito desta equação é chamado
quociente de diferenças. O denominador ∆x é a
variação de x, e o numerador é a variação de y.
Obteremos aproximações cada vez melhores do
coeficiente angular da tangente, escolhendo o
segundo ponto cada vez mais próximo do ponto de
tangência. Observe a sequência de imagens a
seguir.
Isto siginifica que podemos esperar, em novembro,
temperaturas diárias médias mais baixas do que as
14
temperaturas correspondentes em outubro.
17
3. Inclinação e o processo de
limite
3. Inclinação e o processo de
limite
Nos exemplos anteriores aproximamos a
inclinação de um gráfico em um ponto fazendo um
esboço cuidadoso e traçando “a olho” a tangente no
ponto de tangência.
Utilizando
o
processo de limite,
podemos
achar
o
coeficiente
angular
exato da tangente em
(x, f(x)).
Um método mais preciso de obter
aproximação de tangentes consiste em fazer uso
da reta secante pelo ponto de tangência e por um
segundo ponto do gráfico, conforme a figura a
seguir.
15
18
3
3. Inclinação e o processo de
limite
3. Inclinação e o processo de
limite
Nota: ∆x é usada como variável para
representar a variação em x na definição do
coeficiente angular de um gráfico. Podem ser
usadas também outras variáveis. Assim é que esta
definição se escreve às vezes como:
f ( x + ∆x ) − f ( x )
m = lim msec = lim
∆x → 0
∆x →0
∆x
f ( −2 + ∆x ) − f ( −2)
∆x
( −2 + ∆x )2 − ( −2)2
=
∆x
4 − 4∆x + ( ∆x )2 − 4
=
∆x
−4∆x + ( ∆x )2
=
∆x
∆x ( −4 + ∆x )
=
∆x
= −4 + ∆x,
∆x ≠ 0
msec =
Estabelecer o quociente de diferenças
Fazer f ( x ) = x 2
Desenvolver
Simplificar
Fatorar e cancelar
Simplificar
19
3. Inclinação e o processo de
limite
22
3. Inclinação e o processo de
limite
Definição da inclinação de um gráfico:
Em seguida, tomemos o limite de msec quando
∆x → 0.
m = lim msec = lim ( −4 + ∆x ) = −4
A inclinação m do gráfico de f no ponto
(x, f(x)) é igual ao coeficiente angular da tangente
em (x, f(x)) e é dado por
m = lim msec = lim
∆x → 0
∆x → 0
∆x → 0
∆x →0
Assim, o gráfico de f tem inclinação -4 no
ponto (-2, 4), conforme mostra a figura a seguir.
f ( x + ∆x ) − f ( x )
∆x
desde que o limite exista.
20
23
3. Inclinação e o processo de
limite
3. Inclinação e o processo de
limite
Exemplo 3: Determine a inclinação do gráfico de
f(x) = x2 no ponto (-2, 4).
Comecemos achando uma expressão que
represente o coeficiente angular de uma secante
no ponto (-2, 4).
21
24
4
3. Inclinação e o processo de
limite
3. Inclinação e o processo de
limite
Exemplo 4: Ache a inclinação do gráfico de
f(x) = -2x + 4.
Já no Exemplo 4, obtivemos uma fórmula
para a inclinação em um ponto arbitrário do
gráfico. Em tais casos, devemos utilizar x, e não c,
no quociente de diferenças.
Pelo estudo das funções lineares, sabemos
que a reta dada por f(x) = -2x + 4 tem coeficiente
angular -2, conforme a figura a seguir. Esta
conclusão é consistente com a definição de
inclinação como limite.
m = lim
∆x → 0
f ( x + ∆x ) − f ( x )
∆x
Fórmula para a inclinação
Com exceção das funções lineares, esta
forma sempre produz uma função de x, que pode
então ser calculada para se determinar a inclinação
em qualquer ponto que queiramos.
25
28
3. Inclinação e o processo de
limite
3. Inclinação e o processo de
limite
f ( x + ∆x ) − f ( x )
[−2( x + ∆x ) + 4] − [−2x + 4]
= lim
∆x →0
∆x
∆x
− 2 x − 2∆x + 4 + 2x − 4
− 2 ∆x
= lim
= lim
= −2
∆x →0
∆x →0
∆x
∆x
m = lim
∆x →0
Exemplo 5: Determine uma fórmula para a
inclinação do gráfico de f(x) = x2 + 1. Qual é a
inclinação nos pontos (-1, 2) e (2, 5)?
f ( x + ∆x ) − f ( x )
∆x
[( x + ∆x )2 + 1] − [ x 2 + 1]
=
∆x
msec =
3. Inclinação e o processo de
limite
∆x →0
f (c + ∆ x ) − f (c )
∆x
2
2
2
Desenvolver
Simplificar
Fatorar e cancelar
Simplificar
29
3. Inclinação e o processo de
limite
É importante distinguir entre as maneiras
como foram estabelecidos os quocientes de
diferenças nos Exemplos 3 e 4. No Exemplo 3,
determinamos a inclinação de um gráfico em um
ponto específico (c, f(c)). Para achar a inclinação,
podemos utilizar a seguinte forma de um quociente
de diferenças.
m = lim
Fazer f ( x ) = x 2 + 1
x + 2 x ∆x + ( ∆x ) + 1 − x − 1
∆x
2x ∆x + ( ∆x )2
=
∆x
∆x (2x + ∆x )
=
∆x
= 2 x + ∆x,
∆x ≠ 0
=
26
Estabelecer o quociente de diferenças
Inclinação em um ponto
27
Em seguida, tomemos o limite de msec quando
∆x → 0.
m = lim msec = lim (2 x + ∆x ) = 2 x
∆x → 0
∆x →0
Aplicando a fórmula m = 2x, podemos achar
a inclinação em pontos específicos. Em (-1, 2) é
m = 2(-1) = -2, e em (2, 5), é m = 2(2) = 4. A figura
a seguir mostra o gráfico de f.
30
5
3. Inclinação e o processo de
limite
4. A derivada de uma função
Nota: A notação dy/dx se lê “derivada de y em
relação a x” e, utilizando a notação de limite,
podemos escrever
dy
∆y
f ( x + ∆x ) − f ( x )
= lim
= lim
= f ' ( x ).
dx ∆x →0 ∆x ∆x →0
∆x
Além de f’(x), podem ser utilizadas outras
notações para a derivada de y = f(x). As mais
comuns são
dy
,
dx
y ',
d
[ f ( x )] , e
dx
Dx [ y ]
31
4. A derivada de uma função
No
34
4. A derivada de uma função
exemplo
5,
partimos
da
função
Exemplo 6: Ache a derivada de f(x) = 3x2 – 2x.
f(x) = x2 + 1 e utilizamos o processo de limite para
deduzir outra função m = 2x, que representa a
inclinação do gráfico de f no ponto (x, f(x)). Esta
função é chamada a derivada de f em x.
Representa-se por f’ ’(x) e se lê “f linha de x”.
f ( x + ∆x ) − f ( x )
∆x
[3( x + ∆x )2 − 2( x + ∆x )] − [3 x 2 − 2 x ]
= lim
∆x →0
∆x
f ' ( x ) = lim
∆x →0
3 x 2 + 6 x ∆x + 3( ∆x )2 − 2 x − 2∆x − 3 x 2 + 2x
∆x
6 x ∆x + 3( ∆x )2 − 2∆x
= lim
∆x →0
∆x
∆x (6 x + 3 ∆x − 2)
= lim
∆x →0
∆x
= lim (6 x + 3 ∆x − 2)
= lim
∆x →0
∆x →0
32
4. A derivada de uma função
= 6x − 2
35
4. A derivada de uma função
Assim, a derivada de f(x) = 3x2 – 2x é
Definição da derivada:
f ’(x) = 6x – 2.
A derivada de f em x é dada por
f ' ( x ) = lim
∆x →0
Em muitas aplicações, é conveniente
utilizarmos outro símbolo que não x como variável
independente. O Exemplo 7 mostra uma função em
que t é a variável independente.
f ( x + ∆x ) − f ( x )
∆x
desde que o limite exista. Uma função é
diferenciável em x se sua derivada existe em x. O
processo de cálculo de derivadas é chamado
diferenciação.
33
36
6
4. A derivada de uma função
5. Diferenciabilidade e continuidade
Exemplo 7: Ache a derivada de y em relação a t
2
para a função y = .
t
2t − 2(t + ∆t )
2
2
−
dy
f (t + ∆t ) − f (t )
t (t + ∆t )
= lim
= lim t + ∆t t = lim
∆t →0
∆t →0
dt ∆t →0
∆t
∆t
∆t
2t − 2t − 2∆t
−2 ∆t
−2
2
t (t + ∆t )
t (t + ∆t )
= lim
= lim
= lim
=− 2
∆t →0
∆t → 0
∆t →0 t (t + ∆t )
t
∆t
∆t
37
4. A derivada de uma função
40
5. Diferenciabilidade e continuidade
A derivada de uma função dá uma fórmula
para achar o coeficiente angular da tangente em
qualquer ponto do gráfico da função. Por exemplo,
o coeficiente angular da tangente ao gráfico de f
no ponto (1, 2) é dado por
f ' (1) = −
Pela figura anterior, podemos ver que a
continuidade não é uma condição suficientemente
forte para garantir a diferenciabilidade. Todas as
funções exibidas – exceto uma – são contínuas em
(0, 0), mas nenhuma é diferenciável ali. Por outro
lado, se uma função é diferenciável em um ponto,
então ela é contínua aí. Este importante resultado
está englobado no teorema seguinte.
2
= −2
(1)2
38
5. Diferenciabilidade e continuidade
41
5. Diferenciabilidade e continuidade
Nem toda função é diferenciável. A figura a
seguir mostra algumas situações usuais em que uma
função não é diferenciável em um ponto –
tangentes verticais, descontinuidades e reversões
bruscas. As funções apresentadas no gráfico são
diferenciáveis para todos os valores de x exceto
em x = 0.
A diferenciabilidade implica continuidade
Se uma função é diferenciável em x = c,
então ela é contínua em x = c.
39
42
7