Ângulos planos: uma abordagem qualitativa na 5º

Ângulos planos: uma abordagem qualitativa na 5º série
Rodrigo Sychocki da Silva
Mestrando em Ensino de Matemática - UFRGS
A geometria plana é uma parte da matemática que merece atenção dos professores da
educação básica. É nesse estágio, que são apresentadas aos alunos as principais ideias sobre
os elementos da geometria: ponto, reta, ângulo e plano. Em algumas escolas, a geometria é
concebida
como
uma
disciplina
diferente
da
matemática,
e
são
em
períodos
que
complementam a carga horária da matemática que essa disciplina é trabalhada com os alunos.
Essencialmente, vamos nos concentrar no processo de ensino e aprendizagem da noção de
ângulo plano por alunos da 5º série.
A sugestão de VAN HIELE que propõe os chamados níveis de ensino, iniciando com o
processo da visualização ou reconhecimento das estruturas geométricas, que inicialmente não
usa as propriedades intrínsecas das estruturas, são de considerável importância para os alunos
no aspecto da sua aprendizagem sobre ângulos.
A facilidade demonstrada que alguns alunos possuem sobre este assunto remete ao fato
de em sua vivência quotidiana refletir a aplicação de estruturas e raciocínios matemáticos para
a resolução de problemas. Esse aspecto, comentado por HERSCHKOWITZ diz que em uma
experiência realizada com crianças entre 8 e 12 anos que viviam de forma isolada na Índia e
que não tinham tido escolaridade suficiente para a experiência e que também não haviam sido
expostas às convenções dadas pela civilização de certo modo “orientada”, mostrou que a
habilidade dessas crianças estava relacionada ao seu treinamento profissional, que por sua vez
possuía relação explícita com o tipo de ocupação profissional do seu grupo familiar.
Sobre a aprendizagem de geometria, podemos dizer segundo HERSCHKOWITZ que o
início é quando a criança começa a ver e a conhecer o mundo ao seu redor, e isso prossegue
até o pensamento geométrico chegar até um nível onde é possível fazer deduções e inferências
sobre determinados contextos. Por esse motivo, é que no ensino de ângulos planos é
importante que os esforços do professor sejam suficientemente capazes de conduzir os alunos
para a compreensão do assunto de forma a não causar implicações pedagógicas não positivas
futuramente.
O papel da instituição escolar nessa jornada é conciliar os três personagens: aluno,
professor e saber. Essencialmente, segundo LERNER:
(...) é importante que a escola desempenhe a função
de comunicar às novas gerações os saberes socialmente
produzidos,
aqueles
que
são
considerados
válidos
e
relevantes. A comunicação dos conteúdos escolares origina a
relação didática, essa relação ternária que se estabelece
entre professor, aluno e saber. Ao estudar a situação
didática, é preciso levar em consideração, além da natureza
do processo cognitivo da criança, a natureza do saber que
se tenta comunicar e a ação exercida pelo professor para
garantir a comunicação desse saber, para cumprir a função
social a ele atribuída e que o torna responsável pelo
aprendizado dos seus alunos.
No momento em que verificamos a existência de uma proatividade dos alunos, não
podemos desperdiçar a chance de modelar o trabalho do professor de modo que sejam
considerados válido a construção do conhecimento por parte dos alunos. Nesse contexto, a
palavra ensino deve então ser repensada do ponto de vista construtivista. Seus traços
essenciais são considerados por LERNER:
(...) ensinar é colocar problemas a partir dos quais seja
possível reelaborar os conteúdos escolares e também é
fornecer toda a informação necessária para as crianças
poderem avançar na reconstrução desses conteúdos. Ensinar
é promover a discussão sobre os problemas colocados, é
fornecer a oportunidade de coordenar diferentes pontos de
vista, é orientar para a resolução cooperativa das situações
problemáticas.
Ensinar
é
incentivar
a
formulação
de
conceitualizações necessárias para o progresso no domínio
do
objeto
do
conhecimento,
é
propiciar
redefinições
sucessivas até atingir um conhecimento próximo ao saber
socialmente estabelecido.
Para caracterizar como as crianças se apropriam dos conceitos geométricos podemos
dizer que isso ocorre através da relação entre o trio: professor, aluno e saber. A vizinhança,
pais, os elementos externos também contribuem para que haja a apropriação. Para
exemplificar a forma de ensino de geometria vigente, encontramos em livros didáticos de 5º
série uma abordagem sobre ângulos qualitativamente pobre de ideias e que não instigam o
professor a procurar alternativas para alterar esse quadro. De acordo com HERSCHKOWITZ,
podemos dizer que isso ocorre devido a algumas características: falta de completude em sala
de aula (somente parte de exemplos sobre o assunto são apresentados), falta de consciência
por parte do professor e dos livros didáticos (não é apresentado a existência de elementos
adicionais para contribuir no aprendizado), a falta de consciência das dificuldades que existem
do aluno em entender os conceitos, generalização dos atributos realizadas tanto pelo professor
como pelo material didático, onde o aluno é visto como um simples receptor passivo
(contribuindo ainda mais para a dificuldade em entender o conceito).
Abaixo, imagens retiradas de um livro didático que trata do assunto ângulos.
Figura 1 – livro didático de 5º série e o conteúdo ângulos (Parte 1)
Figura 2 – livro didático de 5º série e o conteúdo ângulos (Parte 2)
Uso do Super Logo 3.0 para abordagem sobre Ângulos
O uso da ferramenta SUPER LOGO irá contribuir para a aprendizagem do conceito de
ângulo por alunos de 5º série. Além de ser um software onde o contato direto proporciona um
momento dinâmico de aprendizagem, o software possibilita a inserção do aluno no ambiente
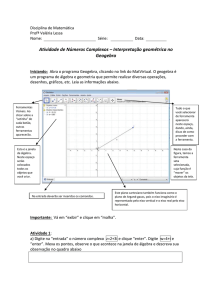
informatizado associado às aulas de matemática. Eis algumas etapas dessa atividade:
1º momento - Familiarização dos alunos com o software e seus comandos básicos PF
(para frente), PT (para trás). Testes de hipóteses, será fornecido uma lista para os alunos com
os questionamentos:
Digite na janela de comando “ pf 100 ”. Descreva o que ocorre:________________ (...)
Aperte o botão limpar. Descreva o que ocorre:________________ (...)
Digite na janela de comando “ pt 100 ”. Descreva o que ocorre:________________ (...)
Aperte o botão limpar.
Digite na janela de comando “ pf 200 ”. Descreva o que ocorre:________________ (...)
Aperte o botão limpar. Descreva o que ocorre:________________ (...)
Digite na janela de comando “ pt 200 ”. Descreva o que ocorre:________________ (...)
Aperte o botão limpar.
Digite na janela de comando “ pf 300 ”. Descreva o que ocorre:________________ (...)
Aperte o botão limpar. Descreva o que ocorre:________________ (...)
Digite na janela de comando “ pt 300 ”. Descreva o que ocorre:________________ (...)
Descreva o que você pode concluir dos comandos “ pf “ e “ pt "._______________ (...)
2º momento - Neste segundo momento serão dados questionamentos do tipo:
1) Inicialmente, siga a seqüência de códigos:
Digite o comando “ pf 100 ”.
Digite o comando “ pf 100 “.
Digite o comando “ pt 100 ”.
Digite o comando “ pt 100 ”.
Digite “ pd 80 ”.
Digite “ pd 40 ”.
Digite o comando “ pf 100 ”.
Digite o comando “ pf 100 ”.
Digite o comando “ pt 100 ”.
Digite o comando “ pt 100 ”.
Há diferença entre os desenhos?Justifique: _______________________ (...)
Descreva por que você acha que ocorreu isso:________________ (...)
Há relação entre os desenhos que você vê? Justifique: __________________ (...)
2) Inicialmente, siga a seqüência de códigos:
Digite o comando “ pf 100 ”.
Digite o comando “ pf 100 “.
Digite o comando “ pt 100 ”.
Digite o comando “ pt 100 ”.
Digite “ pd 45 ”.
Digite “ pd 135 ”.
Digite o comando “ pf 100 ”.
Digite o comando “ pf 100 ”.
Digite o comando “ pt 100 ”.
Digite o comando “ pt 100 ”.
Há diferença entre os desenhos?Justifique: _______________________ (...)
Descreva por que você acha que ocorreu isso:________________ (...)
Há relação entre os desenhos que você vê? Justifique: __________________ (...)
3) Inicialmente, siga a seqüência de códigos:
Digite o comando “ pf 100 ”.
Digite o comando “ pf 100 “.
Digite o comando “ pt 100 ”.
Digite o comando “ pt 100 ”.
Digite “ pd 120 ”.
Digite “ pd 60 ”.
Digite o comando “ pf 100 ”.
Digite o comando “ pf 100 ”.
Digite o comando “ pt 100 ”.
Digite o comando “ pt 100 ”.
Há diferença entre os desenhos?Justifique: _______________________ (...)
Descreva por que você acha que ocorreu isso:________________ (...)
Há relação entre os desenhos que você vê? Justifique: __________________ (...)
4) Inicialmente, siga a seqüência de códigos:
Digite o comando “ pf 100 ”.
Digite o comando “ pf 300 “.
Digite o comando “ pt 100 ”.
Digite o comando “ pt 300 ”.
Digite “ pd 120 ”.
Digite “ pd 120 ”.
Digite o comando “ pf 100 ”.
Digite o comando “ pf 300 ”.
Digite o comando “ pt 100 ”.
Digite o comando “ pt 300 ”.
Há diferença entre os desenhos?Justifique: _______________________ (...)
Descreva por que você acha que ocorreu isso:________________ (...)
Há relação entre os desenhos que você vê? Justifique: __________________ (...)
Qual relação você percebe entre o ângulo e o lado dele? ____________________ (...)
5) Inicialmente, siga a seqüência de códigos:
Digite o comando “ pf 100 ”.
Digite o comando “ pf 300 “.
Digite o comando “ pt 300 ”.
Digite o comando “ pt 900 ”.
Digite “ pd 120 ”.
Digite “ pd 120 ”.
Digite o comando “ pf 100 ”.
Digite o comando “ pf 300 ”.
Digite o comando “ pt 300 ”.
Digite o comando “ pt 900 ”.
Há diferença entre os desenhos?Justifique: _______________________ (...)
Descreva por que você acha que ocorreu isso:________________ (...)
Há relação entre os desenhos que você vê? Justifique: __________________ (...)
Qual relação você percebe entre o ângulo e o lado dele? ____________________ (...)
3º momento - Definição matemática de ângulo, relação do ângulo e sua medida. Esse é o
momento de apresentação do assunto de maneira formal pelo professor. Exemplos de ângulos
importantes no quotidiano.
4º momento - Construção de ângulos usando a ferramenta SUPER LOGO.
Construa os seguintes ângulos:
a) Medida de 60º e os seus lados tem tamanho 100.
b) Medida de 130º e os seus lados tem tamanho 200.
c) Medida de 30º e os seus lados tem tamanho 300.
d) Medida de 25º e os seus lados tem tamanho 400.
e) Medida de 70º e os seus lados tem tamanho 100.
Referências:
ARTIGUE, Michelle. Engenharia didáctica. Retirado do capítulo 4 do livro Didática das
Matemáticas de Jean Brun, Ed. Lisboa, Horizontes Pedagógicos Instituto Piaget, p.193-217;
CARNEIRO, Vera Clotilde GARCIA. Engenharia didática: um referencial para ação
investigativa e para formação de professores de Matemática. Zetetike, Campinas UNICAMP, v. 13, n. 23, 2005, p. 85-118.
HERSCHKOWITZ, Rina. Aspectos Psicológicos da Aprendizagem da Geometria. Boletim
GEPEM, Nª 32.
LERNER, Delia. O ensino e o aprendizado escolar – argumentos contra uma falsa
oposição. Ática, 1995.
MACHADO, Antonio. Iezzi, Gelson. Dolce, Osvaldo. Matemática e realidade 5º. Ensino
Fundamental, Editora Atual.