Estatística e Probabilidades

Estatística e Probabilidades
A distribuição normal nas calculadoras gráficas:
Clicar na ligação que interessa
Texas TI-82/83/84
Casio CFX 9850/9950G
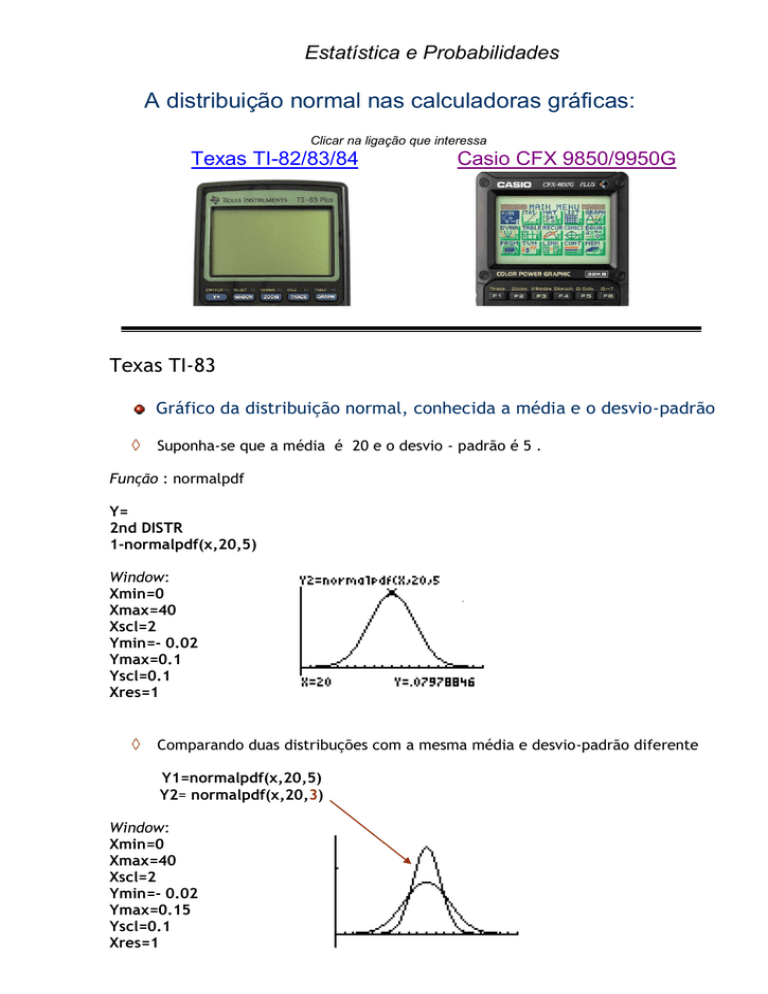
Texas TI-83
Gráfico da distribuição normal, conhecida a média e o desvio-padrão
 Suponha-se que a média é 20 e o desvio - padrão é 5 .
Função : normalpdf
Y=
2nd DISTR
1-normalpdf(x,20,5)
Window:
Xmin=0
Xmax=40
Xscl=2
Ymin=- 0.02
Ymax=0.1
Yscl=0.1
Xres=1
 Comparando duas distribuções com a mesma média e desvio-padrão diferente
Y1=normalpdf(x,20,5)
Y2= normalpdf(x,20,3)
Window:
Xmin=0
Xmax=40
Xscl=2
Ymin=- 0.02
Ymax=0.15
Yscl=0.1
Xres=1
Valor da probabilidade correspondente a um intervalo
i) P(18  X 22)
Neste exemplo calcula-se a percentagem da área sob a curva (*)
que corresponde ao intervalo ] -  ; +  [ i.e. :
sendo
=20 e
=2 ,
P(18  X 22)
(*) Também se diz: probabilidade da variável aleatória assumir valores do
intervalo ]18,22[, numa distribuição normal.
 Cálculo imediato no écran principal
 Função : normalcdf
2nd DISTR
2- normalcdf ( 18,22,20,2)
Resposta : 0,682689
 Graficamente :
Função - ShadeNorm
Sintaxe : ShadeNorm ( limite inferior, limite superior, média, desvio-padrão)
No écran principal:
2nd DISTR DRAW
1- ShadeNorm(18,22,20,2)
ii) P( X  16 )
Basta introduzir no limite inferior um valor suficientemente pequeno.
normalcdf ( 4,16,20,2)
iii) P( X  25 )
Basta introduzir no limite inferior um valor suficientemente grande.
normalcdf ( 25,40,20,2)
Bibliografia:
Brochura: Probabilidades 12º ano Ministério da Educação
Manual da Casio CFX 9850G
Matemática, Editora Contraponto
@M.G.T.Lagido
Casio CFX 9850/9950G
Valor da probabilidade correspondente a um intervalo
Suponha-se que se tem para média e desvio padrão : =20 e  = 2
A distribuição de probabilidade é calculada na Casio pelas funções P(t) e R(t)
cujos gráficos figuram abaixo.
i) P(X ≤ 16 )
Neste exemplo calcula-se a área sob a curva (*) que corresponde ao intervalo
] -  ;16 [ i.e. :
sendo =20
e =2 , P( X  16 )
(*) Probabilidade da variável aleatória assumir valores menores ou iguais a 16,
numa distribuição normal
Usamos a função P(t) , como sugere o gráfico:
Primeiro, calcula-se o valor de t pela fórmula: t =
x-

t = (16-20)/2  t=-2
OPTN
F6( )
F3 (PROB)
F6 ( )
F1 P(-2)
Resposta : P(-2)=0,02275
ii) P( X  25)
Usamos a função R(t) como sugere o gráfico
t= (25-20)/2  t=2,5
OPTN
F6( )
F3 (PROB)
F6 ( )
F1 R(2,5)
Resposta : 0,00621
iii) P(18  X  22)
Calcula-se P(22) - P(18) como em i)
Resposta: 0,68268
Casio CFX 9850/9950G
Gráfico da distribuição de probabilidade:
Suponha-se que queremos visualizar P(X  22)
22-20
t = 1 porque t=
2
Shift F4 ( Sketch)
F5(Graph)
F1(Y=)
OPTN
F6
F3(PROB)
F6
F1 P()
1
Resposta: 0,84134
Bibliografia:
Brochura: Probabilidades 12º ano Ministério da Educação
Manual da Casio CFX 9850G
Matemática, Editora Contraponto
@M.G.T.Lagido