Análise de tensão e deformação

Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
Análise de tensão e
deformação
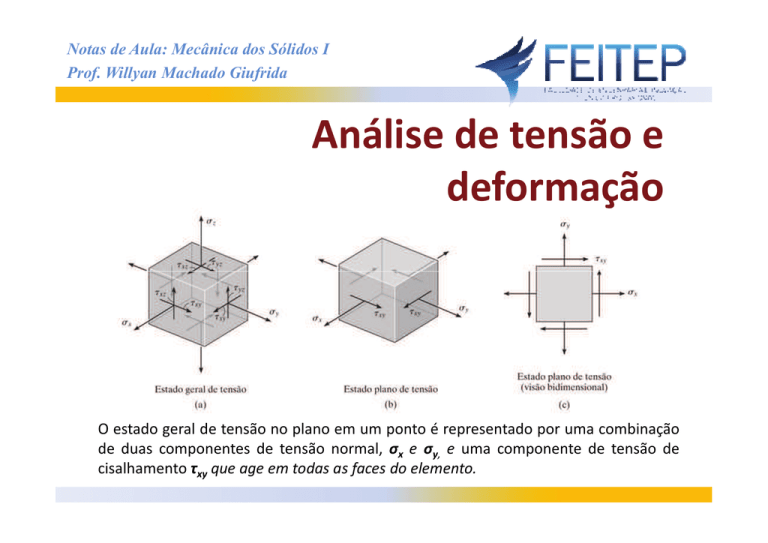
O estado geral de tensão no plano em um ponto é representado por uma combinação
de duas componentes de tensão normal, σx e σy, e uma componente de tensão de
cisalhamento τxy que age em todas as faces do elemento.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
“O estado plano de tensão em um ponto é
representado exclusivamente por três componentes
que agem sobre o elemento que tenha uma
orientação específica neste plano”.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Convenção de sinais
– Uma componente tensão normal ou de cisalhamento é
“positiva” contanto que aja na direção positiva da coordenada
da face positiva do elemento e negativa se for o contrário. Em
resumo, σx e σy é positiva quando age em direção oposta a face
e negativa se age no sentido da face, e τxy será positiva quando
estiver na diagonal com canto superior a direita do elemento,
caso contrário será negativo.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Exemplo:
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Equações gerais de transformação de tensão
no plano.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Determinação do sinal do ângulo
– Se o ângulo de transformação do elemento for
orientado no sentido horário, o mesmo será
“negativo” o contrário será “positivo”.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Regra do topo
– http://web.mst.edu/~mecmovie/
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Exemplo 1: O estado de tensão em um ponto é representado
pelo elemento mostrado na figura. Determine o estado de
tensão no ponto em outro elemento orientado a 30° no
sentido horário em relação à posição mostrada.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Exemplo 2: O estado de tensão em um ponto em um
elemento estrutural é mostrado no elemento. Determine as
componentes de tensão que agem no plano inclinado AB.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Exemplo 3: As fibras da madeira da tábua formam um ângulo
de 20° com a horizontal como mostra a figura. Determine a
tensão normal e a tensão de cisalhamento que agem
perpendicularmente às fibras, se a tábua é submetida a uma
carga axial de 250 N.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Exemplo 4: Uma placa de aço tem espessura de 10 mm e está
sujeita à carga periférica mostrada na figura. Determine a
tensão de cisalhamento máximo no plano e a tensão normal
média desenvolvidas no aço.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Tensões principais e tensão de cisalhamento
máximo no plano
Na prática da engenharia, muitas vezes é importante determinar a
orientação dos planos que fazem com que a tensão normal seja máxima e
mínima e a orientação dos planos que fazem com que a tensão de
cisalhamento seja máxima.
• Tensões principais no plano
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Tensão de cisalhamento máximo no plano e tensão
média
• Orientação dos planos
Os planos para a tensão se cisalhamento máxima podem ser determinados
orientando um elemento a 45° em relação à posição de um elemento que
define os planos da tensão principal.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Exemplo 5: O estado plano de tensão em um ponto sobre um corpo é
mostrado no elemento na figura abaixo. Represente esse estado de tensão
em termos das tensões principais.
Notas de Aula: Mecânica dos Sólidos I
Prof. Willyan Machado Giufrida
• Exemplo 6: O tubo da perfuratriz em diâmetro externo de 75 mm,
espessura de parede de 6 mm e pesa 0,8 kN/m. Se for submetido a um
torque e a uma carga axial como mostra a figura, determine (a) as tensões
principais e (b) a tensão de cisalhamento máxima no plano em um ponto
sobre a sua superfície na seção a.