INTEGRAL DEFINIDO

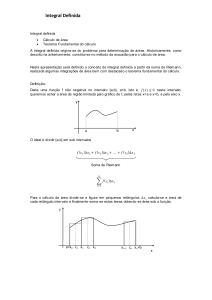
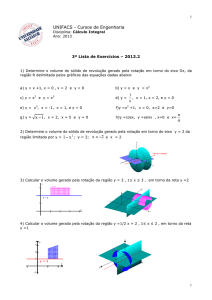
INTEGRAL DEFINIDO
O conceito de integral definido está relacionado com um problema
geométrico: o cálculo da área de uma figura plana.
Vamos começar por determinar a área de uma figura delimitada por
duas rectas verticais, o semi-eixo positivo dos XX e por uma dada
função y = f (x) .
Definição:
Seja f uma função, real de variável real, definida num intervalo
[a, b]. Chama-se partição P desse intervalo a qualquer decomposição
de [a, b] em n subintervalos da forma xi tais que:
a = x0 < x1 < x2 <
< xn = b .
Definição:
Seja f uma função, real de variável real, definida num intervalo
[a, b] e P uma partição desse intervalo. Chama-se Soma de Riemann
de f em relação à partição P, a toda a expressão da forma:
n
i =1
f ( wi )∆xi ,
onde wi é um valor qualquer do intervalo xi .
44
Definição:
Seja f uma função, real de variável real, definida num intervalo
[a, b] e P uma partição desse intervalo. Chama-se integral definido de
b
f desde a até b e escreve-se f ( x) dx , ao limite tal que
a
b
n
f ( x) dx = lim
P → 0 i =1
a
f ( wi )∆xi ,
onde wi é um valor do intervalo ∆ xi .
NOTAS:
1) Se tal limite existe então dizemos que f é integrável no intervalo
[a, b].
2) A a e a b chama-se limites de integração:
a → limite inferior do integral;
b → limite superior do integral.
3) Sempre que utilizamos um intervalo [a, b] supomos que a < b . Mas
a definição anterior pode ser estendida ao caso a > b:
b
a
a
f ( x) dx = − f ( x) dx .
b
a
Como consequência imediata temos o resultado seguinte: f ( x) dx = 0 .
a
45
O teorema que se segue transforma o difícil problema de calcular
integrais definidos por meio de cálculo de limites de somas, num
problema bem mais fácil que se resume, praticamente, na
determinação de uma primitiva da função dada.
Teorema Fundamental do Cálculo:
Seja f uma função, real de variável real, contínua definida num
intervalo [a, b]. Se F é a sua primitiva então
b
f ( x) dx = F (b) − F (a ) .
a
Notação:
b
Pode-se escrever:
b
f ( x) dx = F ( x) |
ou
a
a
b
a
f ( x) dx = [F ( x)] ba .
Propriedades do integral definido
1. Toda a função contínua em [a, b] é integrável em [a, b].
2. Se f é integrável em [a, b] e k é um número real então a função
k f é ainda integrável no mesmo intervalo e tem-se
b
b
k f ( x) dx = k f ( x) dx .
a
a
3. Se f e g são duas funções integráveis em [a, b] então a função
f + g ainda é integrável no mesmo intervalo e tem-se:
b
a
[ f ( x) + g ( x)]dx =
b
a
b
f ( x) dx + g ( x) dx .
a
46
4. Se a < c < b e f é integrável nos intervalos [a, c ] e [c, b] então a
função f é integrável em [a, b] e tem-se:
b
c
b
a
c
f ( x) dx = f ( x) dx + f ( x) dx .
a
5. Se f é integrável num intervalo [a, b] e f ( x) ≥ 0 , ∀x ∈ [a, b], então
b
f ( x) dx ≥ 0 .
a
6. Se f e g são duas funções integráveis em [a, b] e f ( x) ≥ g ( x) ,
b
b
a
a
∀x ∈ [a, b], então f ( x) dx ≥ g ( x) dx .
Nota:
As tabelas e as técnicas de integração utilizadas para o cálculo de
integrais indefinidos são ainda válidas para o cálculo de integrais
definidos.
Exemplo:
Calcule os seguintes integrais definidos:
10
1
a)
dx
2 5x − 1
b)
ln 3
5e x dx
0
47
Mudança de variável no cálculo do integral definido
Seja f uma função contínua no intervalo [a, b]. Pretende-se calcular
b
f ( x) dx por mudança de variável. Seja t a nova variável tal que
a
t = g ( x) .
Quando se faz a mudança de variável os limites de integração, por
dizerem respeito à variável apresentada, deixam de ter significado,
pelo que surge a necessidade de também se efectuar mudanças nos
limites de integração. Para tal, basta calcular os valores
correspondentes de a e b em função da nova variável: t1 = g ( a) e
t 2 = g (b) . Utilizando estes valores torna-se então desnecessário voltar
à variável original x após a integração.
Exemplo: Calcule
5
x −1
dx .
x
1
48
APLICAÇÕES DO CÁLCULO INTEGRAL
Cálculo de áreas
1) Cálculo da área de uma região plana limitada pelo eixo das
abcissas, pelo gráfico de uma função e por duas rectas
verticais
Se f é uma função contínua num intervalo [a, b] e f ( x ) ≥ 0 ,
∀x ∈ [a, b], então a área sob o gráfico de f de a até b é dada por:
b
f ( x)dx .
a
Se f ( x ) ≤ 0 , ∀x ∈ [a, b], então a área sob o gráfico de f de a até b
b
é dada por: − f ( x)dx .
a
Se f muda de sinal em [a, b] um número finito de vezes, então é
dada por:
b
f ( x) dx .
a
y = f (x)
b
a
A
a
A=
A
b
b
a
f ( x )dx
A= −
b
a
f ( x)dx
49
2) Cálculo da área de uma região plana limitada por duas
curvas e por duas rectas verticais
Definição:
Se f e g são funções contínuas no intervalo [a, b] e se f ( x) ≥ g ( x)
∀x ∈ [a, b], então a área da região plana fechada, limitada pelas curvas
y = f (x) , y = g (x) e pelas rectas verticais x = a e x = b , é dada por:
A=
b
[ f ( x) − g ( x)]dx .
a
Nota:
Se falhar a condição f ( x) ≥ g ( x) , A =
b
f ( x) − g ( x) dx .
a
3) Cálculo da área de uma região plana limitada por duas
curvas e por duas rectas horizontais
Definição:
Se f e g forem funções contínuas no intervalo [c, d ] e se f ( y ) ≥ g ( y )
∀y ∈ [c, d ], então a área da região plana fechada, limitada pelas curvas
x = f ( y ) , x = g ( y ) e pelas rectas horizontais y = c e y = d , é dada por
A=
d
[ f ( y ) − g ( y)]dy .
c
Nota:
Se falhar a condição f ( y ) ≥ g ( y ) , A =
b
f ( y ) − g ( y ) dy .
a
50
Exemplos:
a) Calcule a medida da área da região fechada limitada pela função
y = sen ( x ) e pelo eixo das abcissas quando x ∈[0 , 2π ].
b) Calcule a medida da área da região limitada pelas rectas y = 2 x + 1,
1
y = x + 3 e x = 0.
2
c) Calcule a medida da área de um círculo de raio 3.
d) Calcule a área da região fechada limitada pelas funções y = − x + 1,
y = 0 e x = 0.
e) Calcule a medida da área da região fechada compreendida entre os
gráficos das funções y = x 3 e x = y 2 .
51
Cálculo de volumes de sólidos de revolução
Fazendo-se girar uma região plana em torno de uma recta do plano,
o sólido resultante chama-se sólido de revolução. Neste caso, diz-se
que o sólido é gerado pela região e a recta, em torno da qual se
processa a revolução, é chamada eixo de revolução.
Exemplo:
Fazendo-se girar em torno do eixo dos xx uma região limitada pelo
gráfico da uma função contínua não negativa f , pelo eixo dos XX e
pelos gráficos de x=a e de x=b, de acordo com a figura 1, obtém-se
um sólido do tipo exibido na figura 2.
Figura 1
Figura 2
Definição:
Seja f : x → y = f ( x ) uma função, real de variável real, contínua em
[a, b]. O volume V do sólido de revolução gerado pela rotação, em
torno do eixo dos XX, da região limitada pelos gráficos de y = f (x ) ,
x=a, x=b e pelo eixo dos XX é dado por:
V =π
b
a
[ f ( x)]2 dx .
52
Definição:
Seja f : x → y = f ( x ) uma função real de variável real contínua em
[c, d ]. O volume V do sólido de revolução gerado pela rotação, em
torno do eixo dos YY, da região limitada pelos gráficos de x = f ( y ) ,
y=c, y=d e pelo eixo dos YY é dado por:
V =π
d
c
[ f ( y )]2 dy .
Definição:
Sejam f : x → y = f ( x ) e g : x → y = g ( x) funções, reais de variável
real, contínuas em [a, b], com f ( x ) ≥ g ( x ) ≥ 0 . O volume V do sólido
de revolução gerado pela rotação, em torno do eixo dos XX, da região
limitada pelos gráficos de y = f (x ) , y = g (x ) , x=a e x=b é dado por:
V =π
b
a
([ f ( x)]2 − [g ( x)]2 )dx .
Definição:
Sejam f : y → x = f ( y ) e g : y → x = g ( y ) funções, reais de variável
real, contínuas em [c, d ], com f ( y ) ≥ g ( y ) ≥ 0 . O volume V do sólido
de revolução, gerado pela rotação em torno do eixo dos YY, da região
limitada pelos gráficos de x = f ( y ) , x = g ( y ) , y=c, de y=d é dado
por:
V =π
d
c
([ f ( y)]2 − [g ( y)]2 )dy .
53
Exemplos:
a) Calcule a medida do volume do sólido gerado pela rotação da
região do plano limitada pelos gráficos das funções y = x 2 + 1,
y = 0 , x = −1 e x = 1 , em torno do eixo dos xx.
b) A região do plano limitada pelos gráficos das funções y = x ,
y = 2 x e y = x 2 roda em torno do eixo dos xx. Determine a medida
do volume do sólido gerado.
c) Utilizando integrais definidos, prove que o volume de uma esfera
4
3
de raio r é dado por V = πr 3 .
d) Determine o volume do sólido de revolução, gerado pela rotação da
região limitada pelos gráficos de y = x 2 e y = 2 , em torno do eixo
dos yy.
e) Calcule o volume do sólido de revolução, gerado pela rotação em
torno do eixo dos yy, da região limitada por y = x , y = 2 e x = 0 .
f) Utilizando integrais definidos, prove que o volume de um cilindro
circular recto de altura h e raio r é dado por V = πr 2 h .
54
INTEGRAIS IMPRÓPRIOS
A definição de integral definido foi estabelecida para uma função
definida num intervalo [a, b] e contínua nesse intervalo. Vamos agora
considerar os casos: [a,+∞[ , ]− ∞, a ] e ]− ∞,+∞[ . Nestes intervalos não
tem sentido generalizar a definição de integral definido usando somas
de Riemann pois teríamos de usar partições com uma infinidade de
subintervalos.
Exemplos:
Consideremos as funções:
a) f ( x) =
x
, x ∈ [0,+∞[ ;
50
b) g ( x) =
1
x
2
, x ∈ [1,+∞[ .
Definição:
Seja f uma função, real de variável real, definida num intervalo
[a,+∞[ e integrável em qualquer intervalo do tipo [a, X ] com X
arbitrário, superior a a. Se existir lim
que o integral impróprio
+∞
+∞
x →+∞ a
f (x) dx
a
X
f ( x) dx = L então dizemos
é convergente e que
f (x) dx = L.
a
55
Definição:
Seja
f
X
lim
x →+∞ a
[a,+∞[.
uma função contínua no intervalo
Se existir
f ( x) dx = L então dizemos que a área da figura limitada pelo
gráfico de f , pela recta x = a , pelo eixo dos XX e tal que x > a ,existe
e é igual a L.
Nota:
1) No caso do limite não existir ou ser infinito diz-se que o integral
impróprio é divergente ou que a medida da área não existe.
b
2) No caso do integral impróprio
f (x) dx mantém-se tudo o que
−∞
foi dito desde que se considere o limite: lim
b
x →+∞ −Y
f ( x) dx .
Definição:
Seja f uma função integrável em qualquer intervalo fechado. Seja a
um número real qualquer. Se existirem
lim
a
y → +∞ − y
+∞
f ( x) dx = B
−∞
Exemplo: Calcule
x → +∞ a
f ( x) dx = A e
então dizemos que o integral impróprio
f ( x) dx é convergente e que
+∞
lim
X
1
−∞ 1 + x
2
+∞
f ( x) dx = A + B .
−∞
dx .
56
Definição:
Seja f uma função contínua e positiva num intervalo [a, b], excepto
num ponto c, com c ∈ [a, b]. Tem-se que:
b
com
c
y →c −
a
b
a
c
f ( x) dx = f ( x) dx + f ( x) dx ,
a
f ( x) dx = lim
c
y
f ( x) dx
b
e
f ( x) dx = lim
z →c +
c
a
b
f ( x) dx .
z
Quando tais limites existem, diz-se que o integral
Exemplo: Calcule
0
f ( x) dx
a
converge. Caso contrário diverge.
3
b
1
dx .
3− x
Exemplos:
Determine a natureza dos seguintes integrais impróprios:
a)
+∞
e
−x
b)
dx
1
1
+∞
1
−∞ 1 +
x
2
dx
0
1
e)
dx
x
−1
d) ln( x) dx
0
c)
f)
+∞
−∞
1
x
2
x +1
1
−1 x
2
π
g)
2
1x
2
1
(ln( x) )1 / 5
dx
2
h) tan( x) dx
0
i)
1 sen
0
dx
dx
(ln( x) ) dx
x
57
j)
+∞
1
1
dx
x ln( x)
k)
+∞
e−x
−∞ 1 + e
−2 x
dx
+∞
l) sen x dx .
0
58