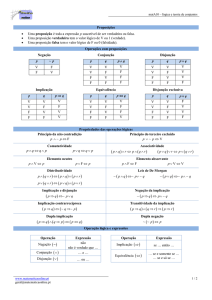
I SEMANA DA MATEMÁTICA
11 a 13 de dezembro 2002
MINICURSO : LÓGICA CLÁSSICA
APLICAÇÕES E CONEXÕES
AULA 1
Um pouco da História da Lógica
Aristóteles (384 – 322 a.C.) é considerado o primeiro a investigar os modos
do raciocínio. Além das estruturas de silogismo investigadas por ele, há o
primeiro uso claro de variáveis em toda a ciência, no enunciado: “Se A é
predicado de todo B e B, de todo C, então, necessariamente, A é predicado de
todo C”.
Estóicos: Crísipo (280 – 205 a.C.) e Filo ( 220 a.C.) são considerados os
responsáveis pelo estudo dos conectivos da linguagem e pela acomodação dos
argumentos aristotélicos em 5 tipos básicos, a seguir:
Se o primeiro, então o segundo
Se o primeiro, então o segundo
O primeiro
Não o segundo
Logo, o segundo
Logo, não o primeiro
Nem o primeiro, nem o segundo
O primeiro
Logo, não o segundo
O primeiro, ou o segundo
O primeiro
Logo, não o segundo
O primeiro, ou o segundo
Não o primeiro
Logo, o segundo
De acordo com Crísipo, um cão, quando possui três caminhos distintos
à sua frente, age da seguinte maneira. Se fareja o primeiro e não lhe serve,
então fareja o segundo. Se este não lhe serve também, o cão ruma pelo
terceiro caminho sem necessidade de verificação. Os cães, segundo ele,
utilizam-se de um argumento do tipo:
O primeiro, ou o segundo, ou o terceiro
Não o primeiro
Não o segundo
Logo, o terceiro
É digno de nota a diferenciação feita entre os dois tipos de disjunção
(inclusiva e exclusiva) e o fato de que o símbolo utilizado atualmente para a
disjunção inclusiva () vem do fato de que, em Latim, a palavra a designar tal
conectivo é a palavra vel (em contraposição à palavra alt, que é utilizada no
caso da disjunção exclusiva)
Argumento de Orígenes (185 – 253)
Eis um argumento divertido, de autoria do filósofo Orígenes de Alexandria:
Se você sabe que está morto, está morto.
Se você sabe que está morto, não está morto.
Logo, você não sabe que está morto.
Leibniz, a Linguagem Natural e a Linguagem simbólica.
O filósofo e matemático Gottfried Wilhelm Leibniz (1646-1716)
dedicou um grande interesse pela lógica e consagrou dignos esforços em um
plano concebido antes que completasse 20 anos de idade. Para Leibniz, a
linguagem comum, sujeita a ambigüidades e imprecisões de toda ordem, não
seria o veículo ideal para a condução das idéias e da comunicação. Se
objetivo passou a ser a construção de uma língua racional, com leis sintáticas
lógicas, criada a partir do levantamento das idéias mais simples, chamadas por
ele de “alfabeto dos pensamentos humanos”, de forma que as idéias mais
complexas pudessem ser desenvolvidas a partir desse “alfabeto”.
Leibniz visava a construção de uma linguagem artificial, que chamava
de Characteristica Universalis (ou Lingua Philosophica), espécie de álgebra
ou matemática generalizada, por meio da qual as estruturas do pensamento e
do raciocínio pudessem ser substituídas pelas estruturas do cálculo. E aparece
em 1666 no livro De arte combinatória.
A presumível execução de seu plano, dava confiança a Leibniz na
possibilidade de desenvolver regras mecânicas que determinariam a solução
de todos os problemas oriundos de imprecisões e dúvidas relativas à
comunicação através da linguagem natural.
“Se tivéssemos isso, seríamos capazes de raciocinar na metafísica e na
moral, do mesmo modo que o fazemos na geometria e na análise. Se
surgissem controvérsias, não haveria mais necessidade de que os filósofos
tivessem mais disputas do que as que ocorrem entre dois peritos em
contabilidade. Pois bastaria que tomassem de seu lápis, sentassem diante de
suas lousas e dissessem um ao outro: calculemos”.
Augustus De Morgan (1806 – 1871) e George Boole (1815 – 1864), lançam
as bases da lógica matemática com os escritos Formal Logic, do primeiro, em
1847 e An Investigation into the Laws of Thought, do segundo, em 1854.
Friedrich Ludwig Gottlob Frege (1848 – 1925), com seus estudos do que
chamava de “Língua Formal do Pensamento Humano” entre 1879 e 1903, é
considerado o recriador da lógica ao elaborar uma teoria dedutiva para o
cálculo e predicados, construindo inúmeras notações, tais como
quantificadores e variáveis que pudessem fornecer fundamentos para a Lógica
Matemática.
A Linguagem Natural e a Lógica
Vejamos alguns casos em que há uma necessidade de maiores cuidados
na transposição entre as linguagens, seja pela ambigüidade da linguagem
natural, seja pela confusão na utilização dos termos.
Uma proposição deve ter o mesmo valor de sua negação dupla:
Hoje é quarta feira não é a negação de Hoje é terça feira
Apesar de ambas satisfazerem à propriedade de uma só ser verdadeira
se a outra for falsa, as duas podem ser falsas simultaneamente.
Alguns alunos não são estudiosos não é a negação de
Alguns alunos são estudiosos
Apesar de ambas satisfazerem à propriedade de uma só ser falsa se a
outra for verdadeira, as duas podem ser verdadeiras simultaneamente
(de fato, consideramos que é o que ocorre com nossas turmas de alunos)
A Conjunção e a propriedade comutativa:
Ela é baiana e maior de idade e Ela é maior de idade e baiana
são proposições equivalentes
Entretanto, tal propriedade (comuntativa) não se dá com
Ela correu e caiu e Ela caiu e correu.
A Conjunção e a divisão em duas proposições:
A proposição Ela é baiana e maior de idade pode ser dividida
nas proposições atômicas Ela é baiana e Ela é maior de idade, sem nenhum
prejuízo da lógica das idéias envolvidas.
Tal não ocorre com a proposição José e Maria são casados, que, se for
substituída por José é casado e Maria é casada, sofre uma alteração na lógica
envolvida.
Alguns paradoxos de linguagem e alguns paradoxos lógicos:
Protágoras de Abdéia ( 480 – 410 a.C), filósofo grego da escola
sofista, é considerado o primeiro filósofo a cobrar por seus ensinamentos. É
atribuído a ele o seguinte paradoxo:
Chamemos de A um advogado e de B seu discípulo. A ministra aulas a
B e combinam que B pagará a A por essas lições. O acordo entre os dois é de
que o pagamento será feito assim que B ganhar uma causa.
Preocupado com a demora que B demonstra em defender qualquer causa, A
processa B, para receber pelas aulas.
Raciocínio de A:
Se eu ganhar, o juiz determina que B me pague;
Se eu perder, B ganhou sua causa, e deve me pagar.
Raciocínio de B:
Se eu ganhar, o juiz determina que nada devo pagar;
Se eu perder, ainda não ganhei uma causa, e portanto...
Eubúlides de Mileto (384 – 322 a.C.) e Epimênides de Creta (século
V a.C.) são responsáveis pelo talvez mais conhecido paradoxo da história da
ciência, o paradoxo do mentiroso.
Eubúlides, contemporâneo de Platão e Aristóteles, adversário deste último
formula o paradoxo da seguinte maneira:
1) “A afirmação que estou fazendo agora é falsa”
Epimênides, da ilha de Creta, afirma que
2) “ Todos os cretenses são mentirosos”
É curioso, mas tal paradoxo parece ter chegado a São Paulo, que cita a
idéia da falsidade, sem contudo considerar o ponto central da lógica
envolvida. Lê-se, na Epístola a Tito: “Um deles, seu próprio profeta, disse
que os homens de Creta são todos mentirosos, criaturas venenosas, vermes
famintos”.
Bertrand Russel (1872 – 1970) é responsável por um paradoxo que
inclusive tem algumas versões populares. Em sua origem, o paradoxo de
Russel se refere a conjuntos. Há conjuntos de dois tipos, os conjuntos que se
contém e os conjuntos que não se contém. O conjunto dos livros não é ele
próprio um livro, assim como o conjunto dos animais não é um animal. São
conjuntos que não se contém. Entretanto, existem conjuntos que se contém,
tais como o conjunto dos conjuntos, que é ele próprio um conjunto, ou o
conjunto das idéias abstratas que é uma idéia abstrata. O paradoxo de Russel
se forma diante da seguinte situação: Chamemos de A o conjunto formado por
todos os conjuntos que não se contém (e somente por esses). A estará contido
em A? Se A se contém, então A não se contém, e se A não se contém, A se
contém.
Esse mesmo paradoxo aparece em outra roupagem, do próprio Russel,
de 1919. Consideremos uma pequena aldeia que possui um barbeiro singular,
que obedece à seguinte regra: ele faz a barba de todos os homens da cidade
que não barbeiam a si próprios (e somente desses). Agora, apreciemos a
pergunta: quem faz a barba do barbeiro? É intrigante considerar que, numa tal
aldeia não pode existir um barbeiro assim, pois, se ele se barbear, estará
fazendo a barba de alguém que se barbeia, o que não satisfaz à regra, ao passo
que, se ele não se barbear, ele terá que ter a barba feita por si próprio, o que
também vai contra o estabelecido.
Em 1908, Leonhard Nelson e Kurt Greeling propuseram uma situação
que se tornou conhecida como o paradoxo de Greeling. Separemos os
adjetivos em duas classes: os adjetivos que se auto-referem serão chamados
de autológicos (proparoxítona, português, polissílabo) e os adjetivos que não
se auto-referem serão chamados de heterológicos (francês, monossílabo,
paroxítona). A palavra “heterológico” é um adjetivo. Em qual dos dois tipos
essa palavra se inclui? Se ela for autológica, então ela se auto-refere, portanto
é heterológica. Se ela for heterológica, ela estará se auto-referindo, sendo
portanto autológica.
Um outro paradoxo curioso, proposto em 1906, conhecido como o
paradoxo de Berry, será adaptado para a língua portuguesa, sem comprometer
a linha de argumentação. Em qualquer língua, cada número inteiro pode ser
descrito com um número de sílabas. O inteiro 352, por exemplo, será descrito
(na forma: “trezentos e cinqüenta e dois”) com 11 sílabas. Para cada inteiro,
existe um número mínimo de sílabas com o qual ele pode ser descrito.
Admitamos que exista um menor número inteiro positivo que não possa ser
descrito com menos do que vinte e oito sílabas e chamemos de P esse número
inteiro. Ora, podemos expressar P como sendo “o menor inteiro positivo que
não se pode expressar com vinte e sete sílabas”, que é uma frase com vinte e
sete sílabas.
O que dizer da frase que expressa “o menor inteiro positivo que não se
pode expressar com menos que trinta e duas sílabas” ?
Em quase todos os paradoxos vistos, aparece o problema de algo que se
refere a si mesmo. A questão que se coloca é de que maneira pode-se fazer
uma auto-referência sem entrar em contradições? Neste minicurso, não há a
pretensão de discutir esse tema, mas, ao aluno interessado em maiores
detalhes a respeito, convém buscar maior aprofundamento, conforme
indicações na bibliografia no final desse texto, acerca dos estudos de Kurt
Gödel (1906 – 1978) e de Alfred Tarski (1902 – 1983), entre outros.
Para escaparmos das ambigüidades da linguagem, teremos que realizar uma
restrição em nosso universo. Simplificando um pouco o processo, diremos
que nossa limitação será nos circunscrevermos às sentenças em que sejam
obedecidos três princípios básicos, que chamaremos de princípios
fundamentais:
O Princípio da Identidade (Uma proposição verdadeira é verdadeira)
O Princípio da Não Contradição (Uma proposição não pode ser
simultaneamente verdadeira e falsa)
O Princípio do Terceiro Excluído (uma proposição ou é verdadeira
ou é falsa)
Assim, qualquer sentença que não obedeça a um desses três princípios
terá que ser descartada em uma análise que utilize a lógica matemática.
Exemplos de proposições que estariam fora do nosso universo de análise:
Esta afirmativa é falsa.
A blusa que estou usando é bonita.
Está frio aqui.
Oba!
Hoje é terça feira?
AULA 2
Os conectivos lógicos e suas tabelas verdade
Negação
p
V
F
~p
F
V
~ ~p
V
F
Vemos acima a tabela verdade da negação de uma proposição.
Assim, se a proposição p é verdadeira, sua negação será falsa e vice-versa. É
necessário termos um certo cuidado na determinação de negações na
linguagem natural, pois uma propriedade a ser satisfeita é a da dupla negação
de uma proposição, que obedece aos mesmos valores verdade da proposição
em si.
Por exemplo, analisemos as proposições “Hoje é terça-feira” e
“Hoje é quinta-feira” , como se uma fosse a negação da outra. É verdade que
se uma for verdadeira, a outra será necessariamente falsa, mas o Princípio do
Terceiro Excluído não está sendo satisfeito, pois há uma possibilidade de
termos uma proposição e sua negação, ambas falsas (aliás, uma chance de 5
em 7, aproximadamente 71%).
Um outro caso a ser detidamente considerado é o da negação de
proposições que utilizam o que os lógicos chamam de quantificadores.
Ponderemos o caso de afirmarmos a partir da intuição, que as proposições
“Alguns alunos são pontuais” e “Alguns alunos não são pontuais” sejam
uma a negação da outra. Observe que ambas as proposições podem ser
simultaneamente verdadeiras (e de fato é o que acontece com nossos alunos!),
não satisfazendo assim o Princípio da Não Contradição. Assim a negação da
primeira proposição deverá ser “Todos os alunos não são pontuais”.
Conjunção
p
V
V
F
F
q
V
F
V
F
pq
V
F
F
F
Também aí é necessário que tomemos cuidados ao traduzirmos de uma
linguagem natural para a linguagem simbólica. A tabela verdade da conjunção
nos fornece a propriedade comutativa para uma tal operação. Assim, a
proposição p q será equivalente a q p.
Consideremos o caso de uma proposição como “Pedro correu e caiu”,
que, de fato, pode ser expressa como a conjunção das duas proposições
atômicas “Pedro correu” e “Pedro caiu”. Até aí, nenhum problema, mas a
proposição encerra um componente implícito de causalidade, pois uma
possível interpretação da sentença é a de que Pedro caiu porque correu. Veja
que se escrevermos “Pedro caiu e correu” a proposição perde esse sentido.
Observe como existe a necessidade de estarmos atentos aos exemplos
mais corriqueiros, tais como “João e Márcia são casados”. O que se dá
quando escrevemos a proposição como uma conjunção das duas proposições
“João é casado” e “Márcia é casada”? Veja como o sentido pode ter
mudado, pois no segundo caso não estamos afirmando que os dois são
casados um com o outro, e na primeira frase, esse sentido é naturalmente
extraído.
Disjunção
p
V
V
F
F
q
V
F
V
F
pq
V
V
V
F
Façamos aqui a necessária distinção entre os dois tipos de disjunção
existentes. Uma delas é o que chamamos de disjunção inclusiva, que
também é nomeada pela expressão e/ou, e que aparece na proposição
“Ela não veio à prova por estar doente ou cansada”, pois é possível
que as duas coisas tenham ocorrido. O outro caso é o da disjunção
exclusiva, também chamada de ou/ou, como em “Ele veio à prova ou
não veio à prova”, em que não é possível que as duas coisas tenham
acontecido. Na tabela verdade acima, tratamos, como se pode verificar,
da disjunção inclusiva.
Implicação
p
V
V
F
F
q
V
F
V
F
pq
V
F
V
V
Se considerarmos a questão da tradução entre as linguagem natural e
simbólica, talvez seja a tabela verdade da implicação a que mais causa
confusões. Em suas duas primeiras linhas, não parece haver problema algum.
Basta tomarmos um exemplo simples, como a proposição “Se fizer sol, irei à
praia”. Analisando a primeira linha da tabela, se de fato fez sol, e fui à praia,
a implicação se torna verdadeira. Mas a frase é admiravelmente falsa se tiver
feito sol e eu não tiver ido à praia, o que obedece ao resultado da segunda
linha. Entretanto, o que dizer da frase “Se fizer sol, irei à praia”, se tivermos
um dia de chuva? Pode-se garantir que não irei à praia? A resposta é que não,
pois a frase afirma algo que certamente acontecerá se fizer sol, mas nada
afirma caso não faça sol.
Mas, ainda assim, quais seriam as razões para que, nesse caso, os
resultados da tabela verdade sejam verdadeiros? Tomemos uma implicação
que tenha uma premissa verdadeira. É evidente que só é possível tirarmos
conclusões verdadeiras daí, o que explica as duas primeiras linhas da tabela.
Por outro lado, e se tivermos uma implicação com uma premissa falsa? De
fato, poderemos ter tanto conclusões verdadeiras como conclusões falsas.
Tomemos um exemplo dado por Bertrand Russel para justificar a quarta linha
da tabela, ou seja, partirmos de uma premissa falsa para chegarmos a uma
conclusão falsa (mantendo a validade do argumento):
“Se 2 = 1, então eu sou o papa”
Demonstração:
Eu e o papa somos 2.
2 = 1.
Logo, eu e o papa somos 1.
E portanto eu sou o papa.
A terceira linha da tabela verdade da implicação afirma ser possível
se partir de uma premissa falsa e a partir dela, se chegar a uma conclusão
verdadeira. Tomemos a implicação “Se 2 = 1, então existe apenas um sol no
nosso sistema solar” . É necessário que se avise que poderíamos provar que
existem quantos sóis quisermos. Mas, como queremos uma conclusão
verdadeira, iremos demonstrar que existe apenas um.
Demonstração:
Ou não existem sóis ou existem sóis.
Caso 1:
Não existem sóis.
2=11=0
Assim, existe um único sol.
Caso 2:
Existem sóis.
Se for um sol, não há o que provar.
Se forem mais de um, basta utilizarmos que
2 = 1 3 = 2 4 = 3 5 =4 ......
Argumentos
Um argumento se define como tendo um certo número de
Premissas (P1, P2, P3, ...., Pn) e uma conclusão C. Vamos tentar determinar o
que se apresenta como sendo um argumento válido e o que se apresenta como
sendo um argumento consistente.
Um argumento é considerado válido se a proposição (P1 P2 ... Pn) C
for uma Tautologia, isto é, tiver todas as linhas de sua tabela verdade com o
resultado V.
Um argumento é considerado consistente se a proposição (P1 P2 ... Pn)
tiver pelo menos uma linha de sua tabela verdade com o resultado V. Em
outras palavras, se não for uma Contradição.
Exercícios :
Verifique a Validade dos Argumentos abaixo:
1)
P1: Penso, logo existo.
P2: Repolhos não pensam.
C : Repolhos não existem.
2)
P1: Se a canoa não virar, eu chego lá.
P2: A canoa virou.
C : Não cheguei lá.
3)
P1: Se a canoa não virar, eu chego lá.
P2: Não cheguei lá.
C : A canoa virou.
4)
P1: Se eu fosse você, eu faria a prova.
P2: Não sou você.
C : Não vou fazer a prova.
5)
P1 : Se Londres não fica na Dinamarca, Paris fica na França.
P2 : Paris não fica na França.
C: Londres fica na Dinamarca.
6)
P1 : Se 6 é par, então 2 não divide 7.
P2 : Ou 5 não é primo, ou 2 divide 7.
P3 : 5 é primo.
C: 6 é ímpar.
7)
P1: Eu amo pelo menos uma das 3 garotas, Ana, Luana ou Maria.
P2: Se eu amo Ana, mas não Maria, então eu também amo Luana.
P3: Ou eu amo Luana e Maria, ou eu não amo nenhuma das duas.
P4: Se eu amo Maria, então eu também amo Ana.
C : Eu amo Luana.
AULA 3
Aplicações
Argumentos falaciosos em política:
P1: Se ele fosse bom governante, a inflação estaria baixa.
P2: A inflação está baixa.
C: Ele é um bom governante.
P1: Se vocês querem pagar impostos mais altos, então votem
no meu oponente.
P2: Vocês não querem pagar impostos mais altos.
C: Não votem no meu oponente.
P1: Se eu for inocente dessas acusações sórdidas de meus
adversários, a Justiça dirá.
P2: Não fui condenando a nada.
C: Sou inocente, honesto e mereço seu voto.
P1: O Congresso Brasileiro está cheio de ladrões
P2: João é congressista brasileiro
C: João é ladrão
P1: Se o governador for inocente, ele irá depor à Justiça.
P2: O governador irá ao Tribunal.
C: O governador é inocente.
Casos complexos em psicologia devido à confusão cotidiana entre as posturas
abaixo (que podem ser, e quase sempre são, ambas falsas)
X é totalmente bom X é totalmente mau
Há que se ter uma distinção necessária entre Contrário e Contraditório
Hoje é terça feira. Hoje é sábado
(contrariedade, pois ambas podem ser simultaneamente falsas)
Hoje é terça feira. Hoje não é terça feira.
(contradição, pois uma é a negação da outra)
“Algumas pessoas sugeriram que a Lógica é perigosa porque leva a
pensar de modo radical. Isso resulta do princípio segundo o qual todo
enunciado ou é verdadeiro ou é falso. Seria melhor, assim prosseguem as
alegações, considerar os enunciados como verdadeiros até certo ponto e falsos
em certa medida, a fim de evitar qualquer espécie de pensamento radical. O
curioso é que essa crítica à lógica se baseia no mesmo erro dos que estão
comprometidos com o pensamento radical: a confusão dos contrários e
contraditórios; “p é verdadeiro” e “p é falso” não são contrários e não devem
ser tratados como tal. Nada existe na Lógica que proponha a confusão entre
contrariedade e contradição; inversamente, o estudo da lógica deve por fim à
confusão”.
Argumentos falaciosos em Propaganda:
ESTATÍSTICA INSUFICIENTE
P1: Y pessoas preferem a marca cccddd.
P2: A marca cccddd é melhor que as outras marcas.
C: A marca cccddd é a melhor.
C’: Compre!!!
AUTORIDADE
P1: X é uma autoridade no assunto.
P2: X usa a marca aaabbb.
C: A marca aaabbb é a melhor.
C’: Compre!!!
TRANSFERÊNCIA DE AUTORIDADE
P1: X é uma autoridade em algo.
P2: X usa a marca aaabbb.
C: A marca aaabbb é a melhor.
C’: Compre!!!
Esportistas, Astros (9 entre 10 estrelas de cinema etc, etc...), Cientistas,
Políticos, Padres, Pessoas Respeitáveis, etc.
AMBIGÜIDADE DOS TERMOS
P1: Só o homem é racional
P2: Nenhuma mulher é homem
C: Nenhuma mulher é racional
O Direito e o comprometimento da logicidade do sistema:
1) Antinomia : Conflito entre normas de mesmo ordenamento
(Princípio da Não Contradição)
Superação de Antinomias
Hierarquia (Federal>Estadual>Municipal)
Especialidade (Tribunal específico da causa>Outro Tribunal)
Cronologia (Mais recente>Mais antigo)
2) Lacuna : Falta de ordenamento jurídico
(Princípio do Terceiro Excluído)
Espaços Jurídicos definidos como
Pleno: condutas referidas no sistema jurídico
Vazio: condutas irrelevantes para o direito (tomar água, chorar)
Superação das lacunas no caso brasileiro: Constituição Federal, artigo 5º, II
Ninguém é obrigado a fazer ou a deixar
de fazer algo senão em virtude da lei.
Além da Lei de Introdução ao Código Civil, artigo 4º
Analogia, Socorro aos Costumes
A - proposições do tipo “Todo X é Y”
E - proposições do tipo “Nenhum X é Y”
I - proposições do tipo “Algum X é Y”
O - proposições do tipo “Algum X não é Y”
A
sub
con
con
al
tra
ter
nos
I
E
c o n t r á r i o s
di
sub
tra
al
di
ter
tórios
tórios
nos
O
s u b c o n t r á r i o s
Comportamentos no Direito:
Obrigatório O(p)
Permitido P(p)
Proibido V(p)
O(p) = V(¬p) = ¬ P(¬p)
V(p) = O(¬p) = ¬ P(p)
P(p) = ¬ O(¬p) = ¬ V(p)
P(¬p) = ¬ O(p) = ¬V(¬p)
O(p)
sub
c o n t r á r i o s
con
al
tra
ter
nos
con
di
tórios
V(p)
sub
tra
al
di
ter
tórios
nos
P(p) s u b c o n t r á r i o s
P(¬p)
Aplicações de Lógicas Não Clássicas:
O Controle de processos industriais foi área pioneira, sendo as primeiras
experiências datadas de 1975 quando foi demonstrado no Queen College, em Londres, que
um controlador nebuloso muito simples conseguiu controlar eficientemente uma máquina a
vapor. Na mesma época, a primeira aplicação industrial significativa foi desenvolvida pela
indústria de cimento F.L.Smidth Corp. da Dinamarca. Hoje em dia, uma grande variedade
de aplicações comerciais e industriais estão disponíveis, destacando-se neste cenário o
Japão e mais recentemente, os EUA e a Alemanha. Dentre os exemplos típicos incluem
produtos de consumo tais como geladeiras (Sharp), ar condicionado (Mitsubishi), câmeras
de vídeo (Canon, Panosonic), máquinas de lavar roupa (Sanyo), aspiradores de pó, etc. Na
indústria automotiva destacam-se transmissões automáticas (Nissan, Lexus), injeção
eletrônica, suspensão ativa, freios antibloqueantes. Sistemas industriais incluem controle
de grupo de elevadores (Hitachi, Toshiba), veículos autoguiados e robôs móveis (Nasa,
IBM), controle de motores (Hitachi), ventilação de túneis urbanos (Toshiba), controle de
tráfego urbano, controle de parada e partida de trens de metrô (Sendai, Tokio). Estas
citações são ilustrativas pois atualmente mais de 1000 patentes envolvendo Lógica Difusa
já foram anunciadas.
Lógicas Trivalentes (V, F ou pode ser)
Lógicas Multivalentes (A Lógica Fuzzy)
Lógica Paraconsistente (Newton da Costa)
Referências sobre a Lógica Clássica:
Kneale, W & M. Kneale – O Desenvolvimento da Lógica. Fundação Calouste
Gulbekian, 3ª edição, 1968.
Suppes, P – Introduction to Logic. Van Nostrand, 1957.
Mendelson, E. – Introduction to Mathematical Logic. Wadsworth & Brooks.
Attie, Joao Paulo – Introdução à Lógica e Aplicações. Ed. Plêiade, 1999.
Referências sobre as Lógicas não Clássicas:
http://www.cwb.matrix.com.br/dbkroeff/
http://www.geocities.com/logicas2000/
http://www.din.uem.br/~ia/controle/fuz_prin.htm
http://www.ai.sri.com/~ruspini/
http://jazz.graco.unb.br/~adolfo/index.html
http://corvo.cpgei.cefetpr.br/~arruda
http://www.flll.uni-linz.ac.at/index.html
http://www.austinlinks.com/Fuzzy/
http://www.abo.fi/~rfuller/ifsa.html