testes não -paramétricos

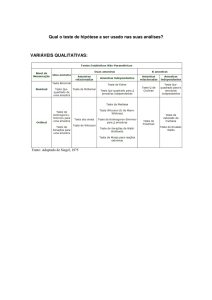
TESTES NÃO - PARAMÉTRICOS
As técnicas da Estatística Não-Paramétrica são, particularmente,
adaptáveis aos dados das ciências do comportamento. A aplicação dessas
técnicas não exige suposições quanto à distribuição da variável populacional. Os
testes não-paramétricos são extremamente interessantes para análises de dados
qualitativos. Na Estatística Paramétrica, para aplicação de teste como o “t” de
Student, a variável em análise precisa ser numérica. Como o próprio nome sugere,
a Estatística Não-Paramétrica independe dos parâmetros populacionais e de suas
respectivas estimativas.
Assim, se a variável populacional analisada não segue uma distribuição
normal e/ou as amostras forem pequenas, pode-se aplicar um teste NãoParamétrico.
Vantagens dos Métodos Não-Paramétricos
1. Os métodos Não-Paramétricos podem ser aplicados a uma ampla
diversidade de situações, porque não exigem populações distribuídas
normalmente.
2. Ao contrário dos métodos Paramétricos, os métodos Não-Paramétricos
podem freqüentemente ser aplicados a dados não-numéricos.
3. Os métodos Não-Paramétricos em geral envolvem cálculos mais simples do
que seus correspondentes Paramétricos, sendo, assim, mais fáceis de
entender.
Desvantagens dos Métodos Não-Paramétricos
1. Os métodos Não-Paramétricos tendem a perder informação, porque os
dados numéricos são freqüentemente reduzidos a uma forma qualitativa.
2. Os testes Não-Paramétricos não são tão eficientes quanto os testes
Paramétricos; assim, com um teste Não-Paramétrico, em geral
necessitamos de uma amostra maior ou maiores diferenças para então
rejeitarmos uma hipótese nula.
1
Teste para Amostras Dependentes (Pareadas)
Teste dos Sinais
É utilizado para análise de amostras dependentes. Logo, esse teste é uma
alternativa para o teste “t” para amostras dependentes. É aplicado em situações
em que o pesquisador deseja determinar se duas condições são diferentes.
O teste do sinal tem pouco poder, pois usa como informação apenas o sinal
das diferenças entre pares. A única pressuposição exigida pelo teste do sinal é a
de que a distribuição da variável seja contínua. Esse teste não faz qualquer
suposição sobre a forma da distribuição das diferenças de médias. É útil nos
trabalhos de pesquisa em que é impossível ou inviável a obtenção de uma
mensuração quantitativa, mas é possível estabelecer postos em relação a cada
um dos dois membros de cada par.
A lógica do teste é que as condições podem ser consideradas iguais
quando as quantidades de "+" e "-" forem aproximadamente iguais.
Procedimento:
a) Formular as hipóteses: a hipótese em teste é a de que as medidas feitas no par
são iguais;
b) Comparar o valor da primeira medida com o valor da segunda medida, feita no
mesmo par de pessoas, animais ou objetos; atribuir o símbolo “+” para todo par de
observações em que a primeira medida for maior do que a segunda e “-“ quando
acontecer o contrário;
c) Contar o número de “+” e de “-“;
d) Para pequenas amostras utilize:
Distribuição amostral. A probabilidade associada de ocorrência é dada pela
1
distribuição binomial com p = q = .
2
d) Para grandes amostras utilize:
Aproximação da distribuição binomial pela normal. Do mesmo modos: p = q =
1
2
2

(x ± 0,5) - 

z=
n
2
n

2
≈ N ( 0,1)
(x + 0,5) é utilizado quando x <
1
1
n e (x − 0,5) é utilizado quando x > n
2
2
x - número de vezes que o sinal menos freqüente ocorre;
n - tamanho da amostra descontando os empates.
Obs.: Diferenças iguais a zero devem ser ignoradas. Essa solução, porém, só é
satisfeita se houver poucos zeros.
O teste dos sinais é fácil de aplicar e praticamente não exige
pressuposições. Mas possui pouco poder.
Siegel (1977) apresenta um estudo referente ao efeito da ausência do pai no
desenvolvimento das crianças. Dezessete casais foram entrevistados, pais e mães
separadamente, e foi verificado o grau de discernimento quanto à disciplina
paterna após o retorno dos pais ao lar, após uma grande ausência. Buscou-se
então verificar se havia ou não diferença entre os cônjuges. Apesar de serem
esperadas diferenças favoráveis à mãe, tendo em vista a ausência prolongada dos
pais, considerou-se como hipótese inicial (nula) a de não diferença entre os pais.
Além disso, três casais foram eliminados do estudo, tendo em vista que o pai e a
mãe apresentaram graus de discernimento considerados iguais. Assim, os
resultados referentes aos 14 casais restantes, as diferenças no grau de
discernimento (Di) e o sinal destas diferenças, representados por 1 se é positivo e
por 0 se este sinal é negativo, são mostrados na tabela 1.
Verifica-se que para 11 casais o grau de discernimento da mãe é superior ao do
pai, ou seja, existe uma forte evidência de que a suspeita dos psicólogos era
correta em relação ao discernimento da autoridade paterna após o retorno ao lar.
1º Passo: Definição das hipóteses.
3
 H 0 : Não existe diferença

 H 1 : Existe diferença
2º Passo: Definição da estatística de teste.
 1
Supondo H 0 como verdadeira: X ~ Binomial  n; 
 2
3º Passo: Introdução dos dados do problema.
Os dados mostram que apenas 14 casais apresentam diferenças então
1

X ~ Binomial  14;  .
2

p = P ( X ≤ 3) = P( X = 0 ) + P ( X = 1) + P ( X = 1) + P ( X = 3) =
14
14
14
 1
1  1
2 1
3  1
= C140   + C14
  + C14   + C14  
 2
 2
 2
 2
14
= 0,029
4º Passo: Definição do nível de significância e construção da região crítica.
α = 5%
Rejeite H 0 se p ≤ 0,05
5º Passo: Conclusão.
Rejeitamos H 0 utilizando 5% de significância.
O exemplo a seguir é apresentado por Siegel (1977).
Suponha que um pesquisador esteja interessado em avaliar se determinado filme
sobre delinqüência juvenil contribui para modificar a opinião de uma comunidade
sobre quão severa deve ser a punição para tais casos. Para isso extrai-se uma
amostra de tamanho 100 e realiza-se um estudo do tipo “antes e depois”. O
resultado encontra-se resumido no quadro abaixo:
4
1º Passo: Definição das hipóteses.
 H 0 : O filme não produz efeito sistemático

 H 1 : O filme produz efeito sistemático
2º Passo: Definição da estatística de teste.

(x ± 0,5) - 

Supondo H 0 como verdadeira: z =
n
2
n

2
≈ N ( 0,1)
3º Passo: Introdução dos dados do problema.
Os dados mostram que 8 + 7 = 15 adultos não modificaram sua opinião. Logo a
hipótese em estudo se aplica somente aos 85 adultos restantes. Desses 85
adultos 26 modificaram a sua opinião de mais para menos enquanto 59
modificaram de menos para mais.
 85 
(26 + 0,5) -  
1
1
 2  = − 3,47
Z Calculado =
pois x < n, isto é, 26 < 85 = 42,5
2
2
85
2
Ou, do mesmo modo:
Z Calculado
 85 
(59 − 0,5) -  
 2  = 3,47
=
85
2
pois x >
1
1
n, isto é, 59 > 85 = 42,5
2
2
5
4º Passo: Definição do nível de significância e construção da região crítica.
α = 5%
Rejeite H 0 se Z Calculado ≤ − 1,96 ou Z Calculado ≥ 1,96
5º Passo: Conclusão.
Como Z Calculado = 3,47 > 1,96 então rejeitamos H 0 utilizando 5% de significância, ou
seja, rejeitamos a hipótese de que o filme não produz um efeito sistemático.
Teste de Wilcoxon
Trata-se de uma extensão do teste dos sinais. É mais interessante pois leva
em consideração a magnitude da diferença para cada par. O teste de Wilcoxon
exige que a variável em análise seja medida em escala ordinal ou numérica, e a
diferença entre duas observações, feitas no mesmo par, também possa ser
ordenada.
Procedimento:
a) Formular as hipóteses: a hipótese em teste é a de que as medidas feitas no
par são iguais;
b) Preparação:
• Calcular a diferença entre a primeira e a segunda medida, feitas no
mesmo par, para todos os pares da amostra. Excluir as diferenças
iguais a zero. Isso significa reduzir a amostra se houver diferenças
iguais a zero;
•
Independentemente do sinal, atribuir um posto a cada diferença; em
caso de empates, atribuir a média dos postos empatados;
•
Atribuir sinais nos postos, respeitando os sinais das diferenças;
•
Obter o valor T que representa a menor das somas de postos de
mesmo sinal;
•
Determinar N que é o total das diferenças com sinal.
c) Cálculo da estatística de teste:
Se N ≤ 25 , obter valor crítico através da tabela apropriada. “Valores críticos da T –
Prova de Wilcoxon”
Exemplo da construção da Tabela de valores críticos para N = 8 .
Casos possíveis: 2 8 = 256
6
Distribuição de freqüência.
7
Se N > 25 , determinar a média e o desvio-padrão aproximado da soma dos
postos. Em seguida, obter o valor de z calculado e o valor de z tabelado. Significa
8
portanto, a utilização da aproximação da distribuição binomial pela distribuição
Normal
z calculado =
sendo: µ T =
T-µ T
σT
N ( N + 1)
4
e
σ
T
=
N ( N + 1)(2 N + 1)
24
d) Critério de decisão:
Se N ≤ 25 ,
Rejeite H 0 se um Tcalculado ≤ Ttabela . Ou seja, rejeite H 0 para todos os valores de T
tão pequenos que a probabilidade associada à sua ocorrência sob H 0 não seja
superior a α % .
Se N > 25 ,
Z
< Zα
Z
> Z α
Para um teste bilateral: Rejeite H 0 se claculado
ou calculado
1−
2
2
Z
> Z α
Para um teste unilateral superior: Rejeite H 0 se calculado
1−
2
Z
< Zα
Para um teste unilateral inferior: Rejeite H 0 se calculado
2
Exemplo: Foram ministrados dois testes similares para verificar o aprendizado. O
objetivo é verificar se os dois testes apresentados são equivalentes. Os testes
foram aplicados ao mesmo grupo de alunos; um no início do período letivo e outro
no fim do período. Os resultados dos testes estão no quadro abaixo.
1º Passo: Definição das hipóteses.
 H 0 : Não existe diferença

 H 1 : Existe diferença
9
2º Passo: Preparação e cálculo da estatística de teste.
O valor T representa a menor das somas de postos de mesmo sinal e o valor de N
que é o total das diferenças com sinal.
N=
T=
8
4
3º Passo: Critério de decisão.
Como a amostra apresenta N ≤ 25, o valor crítico é obtido na tabela dos valores
críticos de Wilcoxon.
Como Tcalculado = 4 > Ttabela = 3 nesse caso não se rejeita-se a hipótese das médias
serem iguais utilizando α = 5% . Repare que o p − valor = 2 ⋅ 0,0273 = 0,0547 > 5% . a
probabilidade associada à sua ocorrência sob H 0 é superior a α % , logo não
podemos rejeitar H 0 .
Obs.: Um ou outro empate não atrapalha o resultado, principalmente se a amostra
é grande. Mas se os empates são muitos, não se pode aplicar a estatística de
teste como definida acima. É preciso usar a fórmula com uma correção para os
empates. Os programas computacionais fazem essa correção automaticamente.
10
Testes Não-Paramétricos para Amostras Independentes
Teste de Mann-Whitney
É usado para testar se duas amostras independentes foram retiradas de
populações com médias iguais. Esse teste é, portanto, uma alternativa para o
teste “t” para amostras independentes quando a amostra for pequena e/ou as
pressuposições, exigidas pelo teste “t”, estiverem seriamente comprometidas. A
única exigência do teste de Mann-Whitney é a de que as observações sejam
medidas em escala ordinal ou numérica.
Procedimento
a) Formular as hipóteses: a hipótese em teste é a de que as medidas feitas no
par são iguais
b) Coloque os dados dos dois grupos em uma única ordenação crescente. Às
observações empatadas atribuir a média dos postos correspondentes;
c) Considerar
n1 = número de casos do grupo 1;
n2 = número de casos do grupo 2;
d) Calcular
= soma dos postos do grupo 1 ;
R2 = soma dos postos do grupo 2 ;
R1
e) Calcular a estatística de Mann-Whitney (U )
n1 ( n1 + 1)
− R1 , ou o que é equivalente:
2
n ( n + 1)
U = n1 n 2 + 2 2
− R2
2
U = n1 n2 +
f) Escolher o menor valor de U, se n < 20 utilizar a tabela de valores críticos
de Mann-Whitney (U ) , caso contrário para ser utilizado no cálculo de z.
z=
U -µ
σ R
R
µ
R
=
n1 ⋅ n2
2
σ
R
=
n1 ⋅ n2 ( n1 + n2 + 1)
12
11
A eficácia da publicidade dos dois produtos concorrentes (Marca X e Marca Y) foi
comparado. Uma pesquisa de mercado realizada em um centro comercial local
ofereceu a cada participante uma xícara de café e depois de degustar cada
participante deu uma nota.
1º Passo: Ordenar as notas:
2º Passo: Calcular
R1 e R2
3º Passo: Calcular Calcular a estatística de Mann-Whitney (U )
12
n1 ( n1 + 1)
6⋅ 7
− R1 = 6 ⋅ 6 +
− 23 = 34 ,
2
2
n ( n + 1)
6⋅ 7
U = n1 n2 + 2 2
− R2 = 6 ⋅ 6 +
− 55 = 2
2
2
U = n1 n2 +
Menor valor de U = 2
4º Passo: Decisão
O valor calculado U = 2 é menos ou igual aos valores da tabela.
Para α = 5% , U Tabela = 5 e para α = 1% , U Tabela = 2
Nesse caso rejeita-se a hipótese nula de igualdade entre as médias populacionais.
Teste Kruskal-Wallis
Trata-se de teste extremamente útil para decidir se k amostras (k > 2)
independentes provêm de populações com médias iguais. Esse teste só deve ser
aplicado se a amostra for pequena e/ou as pressuposições, exigidas para
proceder à Análise de Variância, estiverem seriamente comprometidas. Como o
teste de Mann-Whitney, esse teste também condiciona que a variável em análise
seja medida em escala ordinal ou numérica.
Procedimento
a) Dispor, em ordem crescente, as observações de todos os k grupos, atribuindolhes postos de 1 a n. Caso haja empates, atribuir o posto médio;
b) Determinar o valor da soma dos postos para cada um dos k grupos: Ri, i = 1, 2,
..., k;
c) Escolher uma variável Qui-quadrado com ν = k – 1 (cada amostra deve conter
pelo menos 5 observações);
d) Realizar o teste:
K
( R i ) − 3(N + 1)
12
H=
∑
N(N + 1) i= 1 ni
2
Obs.: Esse teste exige variâncias iguais, por isso não deve ser usado se as
diferentes amostras têm variâncias muito diferentes.
O teste de Kruskal-Wallis é um teste unilateral à direita.
13
Obs.: Quando ocorrem muitos empates, não se deve utilizar a estatística H. É
preciso aplicar uma correção na fórmula. Os aplicativos fazem essa correção
automaticamente. Assim, se mais de um terço dos dados está envolvido em
empates, use um software de estatística.
14
Valores críticos - Teste de Wilcoxon
Fonte: http://www.sussex.ac.uk/Users/grahamh/RM1web/WilcoxonTable2005.pdf
15
Valores críticos - Teste de Mann-Whitney
Fonte:http://www.sussex.ac.uk/Users
16