teoremas de circuitos - corradi.junior.nom.br

TEOREMAS DE CIRCUITOS - Exemplos
III.1 Teorema da Superposição
Em um circuito linear contendo várias fontes independentes, a corrente ou tensão de um
elemento do circuito é igual a soma algébrica das correntes ou tensões dos componentes
produzidas por cada fonte independente operando isoladamente.
Este teorema só se aplica no cálculo de correntes ou tensões e não pode ser utilizado no
cálculo da potência.
Para que se possa operar cada fonte isoladamente, as outras devem ser eliminadas. O
procedimento que deve ser adotado nesta eliminação, das fontes de tensão e fontes de corrente, é
apresentado seguir.
A
A
Curto-Circuito
+
-
EAB = 0
E=0
RAB = 0
B
B
A
A
Circuito-Aberto
I=0
I=0
RAB = ∞
B
B
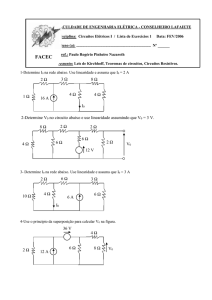
Exemplo 1: Determinar para o circuito abaixo os valores E1, I1, P2, E2, I2 e I3.
E1
+
I1
20 Ω
E2
140 V
I2
I3
6 Ω
5 Ω
18 A
-
Passo 1: Devido à fonte de 140V, abrindo a fonte de corrente tem-se:
E´1
+
I´1
E1’ = 20 I1’
20 Ω
E´2
140 V
I´2
I´3
6 Ω
5 Ω
E2’ = 6 I2’= 5 I3’
LTK ! 140 = E1’ + E2’
-
LCK ! I1’ = I2’ + I3’
Fazendo as substituições tem-se:
E1' E '2 E '2
=
+
20
6
5
Teoremas de Circuitos
 22 
LKT ! 140 =  + 1.E 2´
 3

3E1' = 10E '2 + 12E '2
3E1' = 22E '2 ! E1´ =
22 ´
.E2
3
Tem-se então:
E2’ = 16,8V
I2’ = 2,8A
E1’ = 123,2V
I3’ = 3,36A
I1’ = 6,16A
Passo 2: Devido à fonte de 18A, curto-circuitando a fonte de tensão tem-se:
E´´
1
I´´
1
20 Ω
E´´
2
I´´
2
I´´
3
6 Ω
5 Ω
E1”= 20 I1”
E2”= 6 I2” = 5 I3”
18 A
LTK ! -E1” - E2” = 0
LCK ! I1” + 18 = I2” + I3”
Fazendo as substituições tem-se:
E1"
E" E"
+ 18 = 2 + 2
20
6
5
3E1” + 1080 = - 10E1” - 12E1”
I1”= −
E1” = - 43,2V
E2” = 43,2V
43,2
= −2,16A
20
I2” =
43,2
= 7,20A
6
I3” =
43,2
= 8,64A
5
Passo 3: Devido à superposição tem-se:
E1 = E1’ + E1” = 112,2 - 43,2 = 80V
I2 = 10A
E2 = E2’ + E2’’ = 60V
I3 = 12A
I1 = I1’ + I1” = 4,0A
P2 = 6 (2,8)2 + 6 (7,2)2 = 358W
Levando em consideração este valor de P2, pode-se observar que o Teorema da
Superposição não é válido em relação a potência. Para tanto se deve calcular a potência
dissipada utilizando as fórmulas usuais. Tem-se então:
© Prof. Corradi - www.corradi.junior.nom.br
2/13
Teoremas de Circuitos
P2 = R2 . I 22
ou
P2 = 6.10 2 = 600W
P2 =
V22
R2
P2 =
ou
60 2
= 600W
6
Pode-se observar que a potência dissipada calculada pela fórmula usual não é igual ao
valor encontrado aplicando-se o teorema da superposição comprovando a afirmação feita
anteriormente.
Exercício: resolver o exemplo utilizando o teorema da superposição e os conceitos de divisor de
tensão e corrente que foram apresentados no capítulo anterior.
III.2 Teoremas de Thévenin e Norton
Para que se aplique estes teoremas a uma rede qualquer esta deve ser dividida em duas
partes: X e Y. A rede X deve ser linear e bilateral (2 terminais) e a rede Y deve ser composta por
uma resistência e/ou uma fonte e/ou qualquer ramo. O teorema especifica que a parte X pode ser
substituída por um circuito equivalente de Thévenin ou de Norton. Após o cálculo deste circuito
equivalente, a parte Y deve ser novamente agregada a este circuito equivalente para a solução
final.
Circuito Equivalente de Thévenin
X
Y
X
R Th
A
A
+
VTh
Eth : Tensão de Thévenin
Rth : Resistência de Thévenin
-
B
B
X
Y
X
A
A
IN
Circuito Equivalente de Norton
IN : corrente de Norton
GN
GN: condutância de Norton
B
B
A seguir apresenta-se como calcular os valores dos circuitos equivalentes de Thévenin e
Norton.
•
Eth é a tensão em circuito aberto, medida nos terminais AB. É calculada resolvendo-se
o circuito correspondente considerando as fontes ativas e as resistências do circuito
em relação a estes terminais;
•
RTh é a resistência vista nos terminais AB, quando todas as fontes internas são
anuladas (fonte de tensão = curto-circuito e fonte de corrente = circuito-aberto);
•
IN é a corrente através do curto-circuito aplicado aos terminais AB no sentido A!B;
•
GN é a condutância vista nos terminais AB, quando todas as fontes internas são
anuladas (fonte de tensão = curto-circuito e fonte de corrente = circuito-aberto).
3/13
Teoremas de Circuitos
O conceito de Equivalência de Fontes, apresentado abaixo pode ser utilizado na
resolução de circuitos utilizando-se os teoremas de Thévenin e Norton.
A
R
I
I
+
E0
A
≡
E
-
circuito a
G
I0
B
circuito b
E
B
A seguir se apresenta os cálculos que revelam as relações que devem existir para que as
fontes acima sejam equivalentes.
Se EAB = 0 (curto-circuito)
Circuito b:
Circuito a:
I=
E0
R
I = I0
⇒ E0 = R . I0
Se I = 0 (circuito aberto)
Circuito b:
Circuito a:
E = E0
Então: R =
E=
I0
G
⇒ E0 =
I0
G
E
1
e I= 0
G
R
Exemplo 2: Calcular a fonte equivalente à fonte de tensão apresentada.
10 Ω
A
+
A
≡
30 V
-
0,1 S
3A
B
B
Como o circuito de Norton e o de Thévenin são representações para a mesma fonte física,
para que suas características terminais sejam as mesmas, deve-se ter:
E Th = R Th . I N
R Th =
1
GN
Exemplo 3: Determinar a corrente I no circuito abaixo usando o Teorema de Thévenin.
4/13
Teoremas de Circuitos
20 Ω
+
140 V
I
6 Ω
5 Ω
18 A
-
Para este exemplo considera-se a resistência de 6 Ω como sendo o circuito Y. Para
calcular o circuito equivalente de Thévenin segundo a metodologia apresentada deve-se
retirar o circuito Y (a resistência de 6Ω).
Y
X
20 Ω
+
A
A
5 Ω
140 V
-
18 A
6 Ω
B
B
Cálculo do Equivalente de Thévenin:
ETh = 140 - 20I1
R Th
A
140 - 20 I1 - 5 (I1 + 18) = 0
140 - 25 I1 - 90 = 0
E Th
+
I1 = 2A
-
ETh = 140 - 40 = 100 V
B
Por superposição calcula-se ETh:
ETh = E’ + E”
5
E ' = .140 = 28V
25
5 .18 18
I1” =
= A
25
5
18
E” =
.20 = 72V
5
ETh = 100 V
Calculando agora RTh:
RTh = 20//5 !
20x5
= 4Ω
25
Após ter-se calculado VTh e RTh pode-se
finalmente calcular a corrente no resistor de
6 Ω:
RTh= 4 Ω
+
ETh= 100V
LCK ! I1 - I2 + 18 = 0
6Ω
-
Solução alternativa por Kirchoff:
LTK ! 140 - 20I1 - 5I2 = 0
A
B
I=−
100
! I = −10A
10
III.3 Análise por Correntes de Malha
Este tipo de análise resulta da aplicação das leis de Kirchhoff a circuitos com várias
malhas. As leis de Kirchhoff são aplicadas às correntes das diversas malhas respeitando sentidos
arbitrados (preferencialmente o sentido horário).
5/13
Teoremas de Circuitos
Para exemplificar este procedimento será utilizado o circuito apresentado na figura
abaixo.
R1
Eb
R2
R3
+
-
+
+
Ea
I1
-
R5
R4
I3
I2
-
Ec
Aplicando-se as leis de Kirchhoff tem-se:
Ea - R1I1 - R4 (I1 - I2) = 0
-R2I2 + Eb - R5 (I2 - I3) - R4 (I2 - I1) = 0
-R3I3 - EC - R5 (I3 - I2) = 0
Reescrevendo a primeira equação tem-se:
Ea = (R1 + R4) I1- R4I2
Pode-se observar que R1 e R4 são as resistências que pertencem a malha 1 (resistência
própria) e que -R4 (o coeficiente de I2) é o negativo da resistência existente entre a malha 1 e a
malha 2 (resistência mútua).
Estendendo o mesmo raciocínio para as outras malhas tem-se:
Eb = (R2 + R4 + R5) I2 - R4I1 - R5I3
-Ec = (R3 + R5) I3 - R5I2
Escrevendo os resultados na forma matricial tem-se:
 Ea  R1 + R 4
E  =  −R
4
 b 
- E c   0
− R4
R2 + R4 + R5
− R5
0  I1 
− R 5  I 2  ou seja: E = R .I
 
R 3 + R 5  I 3 
A seguir apresenta-se como, extrapolando os resultados apresentados acima, e baseandose na teoria matemática, pode-se montar diretamente as matrizes E , R e I :
♦ Montagem direta de E :
Ei : é dada pela soma algébrica das fontes de tensão ao se percorrer a malha no
sentido arbitrado para a corrente. A tensão será positiva se a corrente sair pelo
terminal positivo da fonte.
♦ Montagem direta de R :
•
Os elementos da diagonal principal – Rii – são obtidos pela soma das resistências
dos ramos da malha i;
•
Os elementos fora da diagonal principal – Rij – tem o valor da resistência
equivalente do ramo comum à malha i e j com sinal (-).
♦ Montagem direta de I :
A matriz I é o Vetor de corrente de malhas a serem determinadas, arbitradas num
mesmo sentido.
6/13
Teoremas de Circuitos
Exemplo 4: Determinar as correntes de malha para o circuito abaixo:
10 Ω
Utilizando-se
as
regras
apresentadas acima, se obtém a
seguinte equação matricial:
I3
1Ω
2Ω
56 V
-
56  9 −5 −2  I1 
 8  =  −5 10 −1 I 
  
  2
 0  −2 −1 13   I 3 
-
+
5Ω
I1
2Ω
8V
I2
+
4Ω
 9 −5 −2
Calculando o determinante tem-se: ∆ = det  −5 10 −1 = 775
−2 −1 13 
Para o cálculo de I1, deve-se substituir a primeira coluna da matriz ∆ pelo vetor das
tensões (analogamente para o cálculo de I2 e I3). Desta maneira tem-se:
56 − 5 − 2
∆1= det  8 10 − 1  = 7760
 0 − 1 13 
Considerando calculadas ∆1 e ∆2, pode-se calcular as correntes utilizando a Regra de
Cramer:
I1 =
∆1
∆
I2 =
I1 = 10A
∆2
∆
I3 =
I2 = 6A
∆3
∆
I3 = 2A
Casos Particulares:
•
Existência de fontes de corrente em paralelo com uma condutância (resistência) !
efetuar a conversão de fontes
1Ω
5Ω
1Ω
4Ω
2A
≡
5Ω
8V
4Ω
+
• Corrente arbitradas em qualquer sentido ! aplica-se as mesmas regras só que na
montagem de R , os elementos fora da diagonal principal terão sinais positivos se as
correntes nestes elementos estiverem no mesmo sentido.
7/13
Teoremas de Circuitos
+
2Ω
-
I3
4Ω
 7 2 − 4
R =  2 7 3 
− 4 3 9 
3Ω
+
-
1Ω
I1
+
2Ω
2Ω
-
I2
+
-
• Fontes de corrente sem possibilidade de conversão: considera-se que existe uma tensão a
ser determinada nas extremidades das fontes.
10 V
4Ω
I1
E
2A
-
+
2Ω
I2
3Ω
2Ω
4Ω
 E   10
 10  =  − 2

 
 − 20   − 4
−2
7
−9
−
−
4 2 
9I2 
 
9   I 3 
I3
-
+
20 V
3Ω
• Fontes controladas ! monta-se as equações diretamente:
 30   7 −4  I1 
− E = −4 14  -2I 
  
  1
E
3Ω
2.I 1
30 = 7I1 + 8I1 ! I1 = 2A
+
30 V
-
I1
4Ω
I2
10 Ω
logo ! I2 = -4A
-E = -4I1 - 28I1 ! E = 64V
III.4 Análise pelas Tensões nos Nós (Nodal)
Este método permite que se determine a tensão em 2 ou mais nós, em relação a um nó de
referência. Para tanto, as equações decorrentes da LCK são escritas implicitamente, de tal modo
que somente as equações LTK precisem ser resolvidas.
O circuito da figura abaixo é utilizado para demonstrar a análise de um circuito
utilizando-se o método das tensões nos nós.
8/13
Teoremas de Circuitos
E AB
I AB
A
IA
I1
G1
G2
EA
B
IB
EB
I2
G3
Nó de referência
LTK ! EAB - EA + EB = 0 ⇒ EAB = EA - EB
 I − I − I AB = 0 ⇒ I1 = I A + I AB ⇒ I1 = G1 E A + G 2 (E A − E B )
LCK Nós A e B !  1 A
I 2 − I B + I AB = 0 ⇒ I 2 = I B − I AB ⇒ I 2 = G 3 E B − G 2 (E A − E B )
Reescrevendo convenientemente tem-se:
 I1 = (G 1 + G 2 )E A − G 2 E B

I 2 = −G 2 E A + (G 2 + G 3 )E B
 I  G + G 2
Escrevendo na forma matricial: I = G.E !  1  =  1
I 2   − G 2
− G 2  E A 
G 2 + G 3   E B 
A seguir apresenta-se como, extrapolando os resultados apresentados acima, e baseandose na teoria matemática, pode-se montar diretamente as matrizes I , E e G :
♦ Montagem direta de I :
Ii: soma algébrica das fontes de corrente ligadas ao nó i, sendo positivas as que
entram no nó em questão.
♦ Montagem direta de G :
•
Elementos da diagonal principal – Gii – soma de todas as condutâncias ligadas
ao nó i;
•
Elementos fora da diagonal principal – Gij – condutância equivalente conectada
entre os nós i e j, com sinal negativo.
♦ Montagem direta de E :
Ei :faz referência a tensão do nó i em relação ao nó de referência.
Exemplo 5: Determinar para o circuito abaixo as tensões EA e EB utilizando-se o método da
tensão nos nós.
Ref.
A
3Ω
-
+
20/3 A
20 V
A
5Ω
2Ω
+
4Ω
Ref.
2Ω
10 V
0,33 S
2A
0,2 S
0,5 S
B
B
O circuito equivalente, transformando as
fontes é dado por:
9/13
0,25 S
0,5 S
Teoremas de Circuitos
Tem-se que: I = G.E , e desta maneira:
−1 5 −1 2
2 + 20 3 1 5 + 1 2 + 1 3
 − 2  =  −1 3 −1 2
1 5 + 1 2 +1 4 + 1

 
 E A 
.
2  E B 
Resolvendo a equação matricial tem-se: EA = 11,2 V e EB = 4V.
Casos Particulares:
• Existência de fontes de tensão em série com uma resistência: efetuar a conversão de
fontes. Exemplo: calcular as correntes IA e IB da figura a seguir.
4Ω
2Ω
A
B
IA
Matrizes I = G.E :
IB
+
4Ω
4Ω
8V
2A
−1 / 2   E A 
 2  1 / 2 + 1 / 2
=
 −2   −1 / 2
1 / 4 + 1 / 2  E B 
  
-
Nó de referência
2Ω
A
2A
4Ω
4Ω
4Ω
Resolvendo para as tensões tem-se:
B
2 = EA – 1/2 EB
-2 = -1/2 EA +0,75 EB
2A
EA = 1V
Nó de referência
IA
2A
Calculando agora as correntes tem-se:
EB
EA
1/2 S
1
1
x1 = A
4
4
1
1
IB = −2 x
= - A
4
2
IA =
IB
1/2 S
EB = -2V
2A
1/4 S
E0
• Fontes de tensão sem possibilidade de conversão: considera-se que existe uma corrente a
ser determinada para cada fonte.
Resolvendo para o segundo elemento
da matriz I tem-se:
2 = -0,25 . 10 + 0,75 EB
2A
I
A
B
4Ω
0,75 EB = 2 + 2,5
+
5Ω
10 V
-
EA
EB
2Ω
4A
E0
Matrizes I = G.E :
− 1 / 4   10 
 I + 2  1 / 5 + 1 / 4
4 − 2 =  − 1 / 4
1 / 2 + 1 / 4 E B 

 
EB =
4,5
= 6V
0,75
EA = 10V (dado)
Para o primeiro elemento tem-se:
I + 2 = 0,45 . 10 - 0,25 EB
I = 4,5 - 1,5 - 2 ! I = 1A
III.5 Teorema de Millman
O Teorema de Millman apresenta um método usado para reduzir um número qualquer de
fontes de tensão em paralelo a apenas uma. Este teorema constitui um caso especial da aplicação
do teorema de Thévenin. A seguir, a partir de um exemplo este método é apresentado.
10/13
Teoremas de Circuitos
A
R1
R2
+
E1
-
E2
A
RM
R3
+
-
E3
-
EM
+
+
-
B
B
O primeiro passo é transformar os ramos “fonte de tensão/resistência em série” em
“fontes de corrente/condutâncias em paralelo”. Estes cálculos são feitos da seguinte maneira:
A
Gi =
1
Ri
I1
I i = E i Gi
G1
I2
G2
I3
G3
B
A seguir, deve-se calcular o circuito equivalente com uma única fonte de corrente e uma
única condutância. Para tanto os seguintes cálculos devem ser realizados:
I = I1 + I2 - I3
G = G1 + G2 + G3
A seguir apresenta-se este circuito assim como o equivalente de Millman.
A
I
A transformação do circuito fonte de
corrente/condutância em fonte de tensão/resistência
deve ser realizada da seguinte maneira:
G
E M = E AB =
B
RM =
A
1
1
=
G G1 + G 2 + G 3
A tensão entre os pontos AB pode também
ser dada da seguinte maneira:
RM
EM
I +I −I
I
= 1 2 3
G G1 + G 2 + G 3
+
E AB =
-
E1 G1 + E 2 G 2 − E 3 G 3
G1 + G 2 + G 3
B
11/13
Teoremas de Circuitos
Exemplo 6: Determinar a corrente na resistência de 5Ω utilizando o Teorema de Millmam.
Resolver também utilizando o teorema de Thévenin para efetuar uma comparação.
Usando Millman:
A
10 Ω
4V
-
5Ω
+
8V
E AB =
+
-
E AB
4Ω
2Ω
I=−
I
8(1 / 10 ) + 4(1 / 2)
= 2,667V
1 1 1 1
+ + +
10 2 4 5
2,667
= −0,533A
5
B
Usando Thévenin:
A
10 Ω
8V
10 Ω
4Ω
2Ω
+
Eth será calculada utilizando-se o
teorema da superposição.
A
4 × 8 20 × 4
ETh = E AB = 3
+ 7
4
20 + 2
10 +
3
7
10,67 11,43
ETh =
+
= 3,29 V
11,33 4,86
+
-
4V
4Ω
2Ω
-
B
B
A
Rth será calculada utilizando-se o procedimento padrão
descrito.
10 Ω
2Ω
4Ω
1
1 1 1
=
+ +
R Th 10 2 4
B
1
= 0,85
R Th
R Th = 11765
,
Ω
Tendo calculado ETh e RTh pode-se finalmente calcular a corrente I.
R = 1,1765 Ω A
Th
I=
+
E = 3,29 V
Th
-
5Ω
I
I=−
ETh
RTh + RC
3,293
= −0,533A
1.1765 + 5
B
III.6 Teorema da Máxima Transferência de Potência
Este teorema é utilizado quando em uma rede elétrica deseja-se obter a máxima
transferência de potência da rede para uma carga resistiva RL.
Para se calcular esta máxima transferência de potência utiliza-se o equivalente de
Thévenin da rede para determinar a corrente I que passa pela carga RL. O circuito apresentado a
seguir mostra um exemplo.
12/13
Teoremas de Circuitos
R
A
Th
+
R
E
Th
-
I=
L
I
E Th
R Th + R L
B
A potência absorvida pela carga será:
PL = R L I =
2
R L E Th 2
(R Th + R L )2
E Th 2   R Th − R L  
=

1 − 
4 R Th   R Th + R L  
A potência transferida PL será máxima quando RL = RTh, ou seja, quando a carga for igual ao
valor da resistência equivalente de Thévenin do circuito. Neste caso a potência em RTh será
2
E Th
e assim pode-se afirmar que quando a potência transferida é a máxima, a eficiência do
4R Th
circuito é de 50%.
13/13
COTUCA - www.corradi.junior.nom.br
ELETRICIDADE BÀSICA
ELETRICIDADE BÁSICA
TEOREMAS DA ANÁLISE DE CIRCUITOS
INTRODUÇÃO
Serão apresentados os teoremas fundamentais da análise de circuitos. Isto inclui
os teoremas da superposição, de Thévenin e de Norton.
TEOREMA DA SUPERPOSIÇÃO
O teorema da superposição, bem como os métodos vistos anteriormente, pode ser
usado para encontrar a solução para circuitos contendo uma ou mais fontes que não
estejam em série nem em paralelo. A vantagem mais evidente deste método é dispensar
o uso de ferramentas matemáticas, como os determinantes, para calcular as tensões e
correntes solicitadas. Em vez disso, o efeito de cada fonte é levado em conta
separadamente e o valor da incógnita é obtido efetuando a soma algébrica desses
efeitos individuais.
O enunciado do teorema da superposição é o seguinte:
A corrente através de um elemento, ou a tensão entre seus terminais, em um
circuito linear bilateral é igual à soma algébrica das correntes ou das tensões
produzidas independentemente por cada uma das fontes.
Ao se aplicar o teorema, é possível considerar os efeitos de duas fontes ao
mesmo tempo e reduzir o número de circuitos a serem analisados. Mas, em geral:
Números de circuitos
a serem analisados
Números de fontes
independentes
=
Para considerar os efeitos de cada fonte independentemente, é necessário que
estas sejam removidas e substituídas sem afetar o resultado final. Uma fonte de tensão,
na aplicação do teorema, deve ser substituída por um curto-circuito e uma fonte de
corrente deve ser substituída por um circuito aberto.
A corrente total em qualquer parte do circuito é a igual à soma algébrica das
correntes que seriam produzidas separadamente por cada uma das fontes
O princípio da superposição não pode ser usado para calcular a potência
dissipada em um circuito, já que a dissipação de potência em um resistor varia com o
quadrado da corrente ou da tensão, sendo, portanto um efeito não-linear.
EXEMPLO NUMÉRICO
1. Determinar a corrente I1 para o circuito da Figura 1.
Solução:
Figura 1 – Circuito do exemplo 1.
Fazendo E = 0 V no circuito visto na
Figura 1, obtém-se o circuito mostrado
na Figura 2. Notar que toda a corrente
fornecida pela fonte de 3 A irá passar
pelo ramo onde está o curto-circuito e
assim I’1 = 0.
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
1
Figura 2 – Contribuição de I para I1.
Substituindo-se a fonte de corrente por
um circuito aberto, obtém-se o circuito
mostrado na Figura 3. Aplicando a lei
de Ohm:
E 30 12
I1'' 


 I1''  5 A
R1 6
4
Como I’1 e I”1 têm o mesmo sentido, a
corrente I1 é dada pela soma dessas duas
correntes:
I1  I1'  I1''  0  5  I1  5 A
Note que neste caso a fonte de corrente
não afeta a corrente no resistor. A
tensão entre os terminais do resistor é
30 V, pois ele está em paralelo com a
fonte de tensão.
Figura 3 – Contribuição de E para I1.
EXEMPLO NUMÉRICO
2. Usando o teorema da superposição, determinar a corrente no resistor de 4 Ω na Figura 4.
Solução:
Considerando os efeitos da fonte
de 54 V (ver Figura 5):
R T  R 1  R 2 || R 3  24  12 || 4 
24  3  R T  27 
Figura 4 – Circuito do exemplo 2.
Figura 5 – Efeito de E1 sobre a corrente I3.
E1 54

 I  2A
R T 27
Usando a regra dos divisores de corrente:
R2  I
12  2 24
I3' 


 I3'  1,5 A
R 2  R 3 12  4 16
Considerando agora os efeitos da fonte de 48 V (ver Figura 6):
I
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
2
R T  R 3  R 1 || R 2  4  24 || 12  4  8  R T  12 
Figura 6 – Efeito de E2 sobre a corrente I3.
E 2 48

 I  4A
R T 12
A corrente resultante no resistor de 4 Ω é:
I 3'' 
I 3  I 3' '  I '3  4  1,5  I 3  2,5 A no sentido de I”3.
EXEMPLO NUMÉRICO
3. Usando o teorema da superposição,
determinar a corrente I2 no resistor de
12 kΩ na Figura 7.
Solução:
Considerando o efeito da fonte de
corrente de 6 mA (ver Figura 8) e
aplicando a regra dos divisores de
corrente:
I '2
Figura 7 – Exemplo 3.
R1  I
6000  6  10 3


 I '2  2 mA
R 1  R 2 6000  12000
Considerando o efeito da fonte de 9 V
(ver Figura 9):
E
9
I '2' 

 I '2'  0,5 mA
R 1  R 2 6000  12000
Figura 8 – Efeito da fonte de tensão sobre a
corrente I2.
Figura 9 – Efeito da fonte de corrente sobre a corrente I2.
NOTAS DE AULA - TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
3
Como I’2 e I”2 têm o mesmo sentido em R2, a corrente desejada é dada pela soma
dessas duas correntes:
I 2  I '2  I '2'  2 mA  0,5 mA  I 2  2,5 mA
TEOREMA DE THÉVENIN
O teorema de Thévenin afirma que:
Qualquer circuito de corrente contínua bilateral de dois terminais
pode ser substituído por um circuito equivalente constituído por
uma fonte de tensão e um resistor em série.
Na Figura 10(a) o circuito no interior da caixa só está ligado o exterior por dois
terminais, que denominamos a e b. Usando o teorema de Thévenin, é possível substituir
tudo o que existe no interior da caixa por uma fonte e um resistor, como mostrado na
Figura 10(b), sem mudar as características do circuito entre os terminais a e b. Ou seja,
qualquer carga conectada aos terminais a e b se comportará da mesma maneira se
estiver conectada ao circuito da Figura 10(a). Nos dois casos a carga receberá a mesma
corrente, tensão e potência.
Figura 10 – Efeito da aplicação do teorema de Thévenin.
Para o circuito mostrado na Figura 10(a), o circuito equivalente de Thévenin
pode ser determinado diretamente combinando as baterias e resistores em série. Mas, na
maioria dos casos, existem outros elementos conectados à direita ou à esquerda dos
terminais a e b. Entretanto, para aplicar o teorema, o circuito a ser reduzido à sua forma
equivalente de Thévenin tem de ser isolado como mostra a Figura 10, e os terminais ‘de
conexão’ identificados.
A aplicação desse teorema permite determinar qualquer valor particular de tensão
ou corrente num circuito linear com uma, duas ou qualquer outro número de fontes. É
possível também separar uma parte de um circuito, substituindo-o pelo equivalente de
Thévenin. Por exemplo, na Figura 11, após se obter o circuito equivalente de Thévenin
para a parte sombreada, pode-se calcular facilmente a corrente no resistor variável RL e
a tensão entre seus terminais para qualquer valor que RL possa assumir.
Na Figura 11, todo o circuito, com exceção de RL, deve ser substituído por uma
bateria e um resistor em série. Os valores desses dois componentes do circuito
equivalente têm de ser escolhidos de modos a garantir que o resistor RL se comporte, no
circuito visto na Figura 11(a), da mesma forma que no circuito mostrado na Figura
11(b). Em outras palavras, a corrente e tensão no resistor RL devem ser as mesmas para
os dois circuitos para qualquer valor de RL.
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
4
Figura 11 – Substituição de um circuito complexo pelo circuito equivalente de Thévenin.
Os passos do método são os seguintes:
1. Remove-se a parte do circuito para a qual deseja obter o equivalente Thévenin.
No caso da Figura 11(a), é necessário remover temporariamente o resistor RL.
2. Assinalam-se os terminais do circuito remanescente.
3. Calcula-se RTh, colocando primeiro todas as fontes em zero (substituindo as
fontes de tensão por curtos-circuitos e as fontes de corrente por circuitos
abertos) e em seguida determine a resistência equivalente entre os dois
terminais escolhidos.
4. Calcula-se ETh retornando primeiro todas as fontes às suas posições originais
no circuito e em seguida determinando a tensão entre os dois terminais
escolhidos, mantendo o circuito aberto entre os terminais a e b.
5. Desenha-se o circuito equivalente de Thévenin e recoloca-se entre os terminais
do circuito equivalente a parte que foi previamente removida.
EXEMPLO NUMÉRICO
4. Determinar o circuito equivalente de Thévenin para a parte sombreada do circuito da
Figura 12. Em seguida, determinar a corrente em R L considerando que essa
resistência tenha valores de 2 Ω, 10 Ω e 100 Ω.
Solução:
Os passos 1 e 2 levam ao circuito
da Figura 13.
Figura 12 – Circuito do exemplo 4.
Figura 13 – Circuito após a aplicação dos
passos 1 e 2.
Passo 3: Substituindo-se a fonte de tensão E1 por um curto-circuito, obtém-se o
circuito da Figura 14(a), onde:
R Th  R 1 || R 2 
36
 R Th  2 
3 6
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
5
Passo 4: Introduz-se novamente a fonte de
tensão (ver Figura 15). Neste exemplo, a
tensão de circuito aberto ETh é a mesma que
a queda de tensão entre os terminais da
resistência de 6 Ω.
Aplicando a regra dos divisores de tensão:
R2 E
6  9 54
E Th 


 6V
R 2  R1 6  3 9
Passo 5, ver Figura 16:
E Th
IL 
R Th  R L
6
R L  2   IL 
 1,5 A
22
6
R L  10   I L 
 0,5 A
2  10
6
R L  100   I L 
 0,059 A
2  100
Se não fosse possível a aplicação do
teorema de Thévenin, cada mudança no
valor de RL necessitaria de que todo o
circuito mostrado na Figura 12 fosse analisado para se determinar os valores de
tensão e corrente em RL.
Figura 14 – Determinação de RTh.
Figura 15 – Determinação de ETh.
Figura 16 – Substituição do circuito externo a RL
pelo circuito equivalente de Thévenin.
EXEMPLO NUMÉRICO
5. Determinar o circuito equivalente de Solução:
Thévenin para a parte sombreada do Os passos 1 e 2 levam ao circuito da
circuito da Figura 17.
Figura 18.
Figura 17 – Circuito do exemplo 5.
Figura 18 – Circuitos após os passos 01 e 02..
Passo 3 (ver Figura 19): Neste caso, a substituição da fonte de tensão E por um
curto-circuito estabelece uma conexão direta entre os pontos c e c’ na Figura 19(a),
o que permite ‘dobrar’ o circuito, tendo como eixo a reta horizontal que liga a e b,
resultando no circuito mostrado na Figura 19(b).
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
6
Então:
R Th  R a  b 
R 1 || R 3  R 2 || R 4 
6 || 3  4 || 12  2  3
R Th  5 
Figura 19 – Determinação de RTh.
Passo 4: O circuito redesenhado é mostrado na Figura
20. A ausência de uma conexão direta entre a e b resulta
em um circuito com três ramos em paralelo. Portanto as
tensões V1 e V2 podem ser
determinadas usando a regra
dos divisores de tensão:
R1  E
6  72 432
V1 


 V1  48 V
R1  R 3 6  3
9
Figura 20 – Determinação de ETh.
R2  E
12  72 864


 V2  54 V
R 2  R 4 12  4 16
Considerando a polaridade indicada na Figura 20 para ETh e aplicando a LKT à
malha superior no sentido horário, obtém-se:
 V   E Th  V1  V2  0  E Th  V2  V1  54  48  E Th  6 V
V2 
Passo 5: Ver Figura 21
Figura 21 – Circuito equivalente de Thévenin.
A aplicação do teorema de Thévenin não
se restringe a apenas um elemento passivo,
como mostrado nos exemplos anteriores, pois
ele pode ser aplicado em fontes, ramos inteiros,
partes dos circuitos ou qualquer configuração
de circuito. Pode acontecer também que seja
necessário utilizar um dos métodos anteriores,
como o das malhas ou da superposição para
determinar o circuito equivalente de Thévenin.
EXEMPLO NUMÉRICO
6. Determinar o circuito equivalente de Thévenin para a parte sombreada do circuito da
Figura 22.
Solução:
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
7
O circuito é redesenhado e os
passos 1 e 2 são aplicados como
mostra a Figura 23.
Passo 3: Ver Figura 24.
R Th  R 4  R 1 || R 2 || R 3
R Th  1400  800 || 4000 || 6000
R Th  1400  800 || 2400
R Th  1400  600 
R Th  2000 
Figura 22 – Circuito do exemplo 6.
Passo 4: Aplicando o teorema
da superposição, serão considerados primeiro os efeitos da
fonte de tensão E1 (ver Figura
25).
O circuito aberto faz com que
V4 = I4∙R4 = 0∙R4 = 0 V e:
E 'Th  V3 e
R 'T  R 2 || R 3  4000 || 6000
Figura 23 – Circuito da Figura 22 redesenhado.
R 'T  2400 
Aplicando a regra dos divisores
de tensão:
V3 
R 'T  E1

2400  6

2400  800
R 'T  R 1
14400
V3 
 V3  4,5 V  E 'Th
3200
Figura 24 – Determinação de RTh.
A aplicação do método da
superposição para a fonte E2
resulta no circuito mostrado na
Figura 26. Novamente tem-se
V4 = I4∙R4 = 0∙R4 = 0 V e:
'
E 'Th
 V3
R 'T'  R 1 || R 3  800 || 6000 
R 'T'  706 
Figura 25 – Contribuição da tensão E1 para ETh.
Aplicando a regra dos divisores de tensão:
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
8
V3 
R 'T'  E 2
R 'T'  R 2

706 10
7060
'

 V3  1,5 V  E 'Th
706  4000 4706
Como E’Th e E”Th têm polaridades opostas:
'
E Th  E 'Th  E 'Th
 4,5  1,5  E Th  3 V
Passo 5: Ver Figura 27.
Figura 27 – Circuito equivalente de Thévenin.
Figura 26 – Contribuição da tensão E2 para ETh.
TEOREMA DE NORTON
Já foi visto que para qualquer fonte de
tensão em série com uma resistência interna
é possível se determinar uma fonte de
corrente equivalente. O circuito com fonte
de corrente equivalente ao circuito de
Thévenin, como mostra a Figura 28, pode
ser obtido com o auxílio do teorema de
Norton.
Figura 28 – O circuito equivalente de Norton.
O teorema de Norton afirma que:
Qualquer circuito de corrente contínua linear bilateral de dois
terminais pode ser substituído por um circuito equivalente formado por
uma fonte de corrente e um resistor em paralelo
Os passos do método são os seguintes:
1. Remove-se a parte do circuito para a qual deseja obter o equivalente de
Norton.
2. Assinalam-se os terminais do circuito remanescente.
3. Calcula-se RN, colocando primeiro todas as fontes em zero (substituindo as
fontes de tensão por curtos-circuitos e as fontes de corrente por circuitos
abertos) e em seguida determine a resistência equivalente entre os dois
terminais escolhidos. Nota-se que este passo é idêntico ao que foi descrito para
o teorema de Thévenin.
4. Calcula-se IN retornando primeiro todas as fontes às suas posições originais no
circuito e em seguida determinando a corrente de curto-circuito entre os dois
terminais escolhidos. Esta corrente é a mesma que seria medida por um
amperímetro conectado entre os terminais assinalados.
5. Desenha-se o circuito equivalente de Norton e recoloca-se entre os terminais
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
9
do circuito equivalente a parte que foi previamente removida.
Pode-se obter o circuito equivalente de Norton a partir do circuito equivalente de
Thévenin e vice-versa utilizando as técnicas de transformação de fontes, discutidas
anteriormente e reproduzidas na Figura 29.
Figura 29 – Determinação de RTh.
EXEMPLO NUMÉRICO
7. Determinar o circuito equivalente de
Norton para a parte sombreada do
circuito da Figura 30.
Solução:
Os passos 01 e 02 são mostrados na
Figura 31.
O passo 3 é mostrado na Figura 32
3 6
R N  R1 || R 2 
 2
3 6
Figura 31 – Identificação dos terminais de interesse.
Figura 30 – Circuito do exemplo 7.
Figura 32 – Determinação de RN.
O passo 4 é mostrado na Figura 33,
indicando claramente que o curtocircuito entre os terminais a e b está
em paralelo com R2, eliminando
qualquer efeito dessa resistência.
Portanto IN é a corrente que atravessa
R1, já que:
V2  I 2  R 2  0  6  V2  0 V
Portanto: I N 
E 9
  IN  3A
R1 3
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
Figura 33 – Determinação de IN.
10
Passo 5: Ver Figura 34. Este circuito é
o mesmo no qual foi aplicado o
teorema de thévenin inicialmente. Uma
simples conversão indica que os
circuitos de Thévenin e Norton são, de
fato, os mesmos (ver Figura 35).
Figura 34 – Determinação de RTh.
Figura 35 – Conversão entre os circuitos equivalentes de Norton e de Thévenin.
EXEMPLO NUMÉRICO
8. Determine o circuito equivalente de Norton para a parte do circuito à esquerda dos
pontos a e b vistos na Figura 36.
Figura 36 – Circuito do exemplo 8.
Solução:
Passos 1 e 2 ver Figura 37.
O passo 3 é mostrado na Figura 38 e:
46
R N  R1 || R 2 
 2, 4 
46
Figura 37 – identificação dos terminais de saída.
Figura 38 – Determinação de RN.
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
11
Passo 4: (Usando o teorema da
superposição).
Para a bateria de 7 V (ver Figura
39):
E
7
I 'N  1   I 'N  1,75 A
R1 4
No caso da fonte de 8 A (ver
Figura 40), tem-se que tanto R1
quanto R2 foram curto-circuitadas
pela ligação direta entre a e b e:
Figura 39 – Contribuição da fonte de tensão E1.
I ''N  I  8 A
I N  I''N  I 'N  8  1,75 
I N  6,25 A
Passo 5: ver Figura 41.
Figura 40 – Contribuição da fonte de corrente I.
Figura 41 – Circuito equivalente de Norton.
BIBLIOGRAFIA
Boylestad, R. L. – INTRODUÇÃO À ANÁLISE DE CIRCUITOS – 10ª Edição.
Capítulo 9. Pearson Education do Brasil. São Paulo / SP. 2004.
NOTAS DE AULA – TEOREMAS DA ANÁLISE DE CIRCUITOS – REV. 1
12