Algebra de blocos e representacao de sistemas

B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Função de Transferência – Relação Entrada-Saı́da
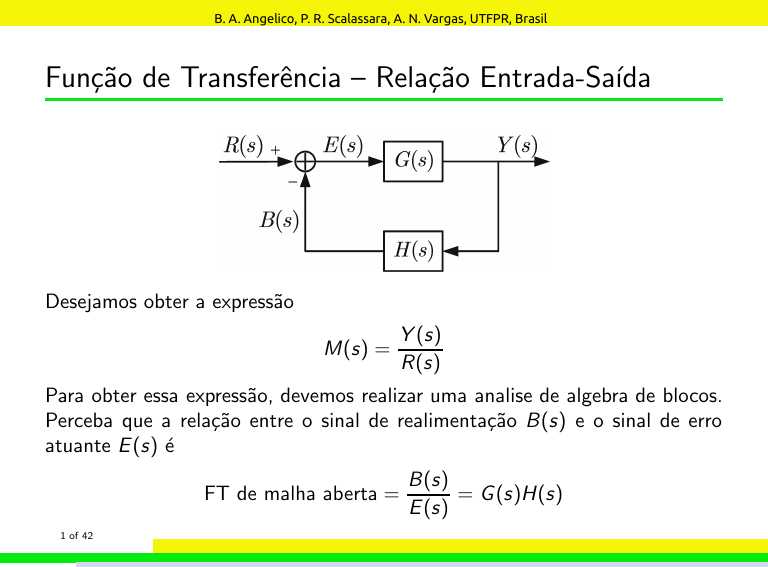
Desejamos obter a expressão
M(s) =
Y (s)
R(s)
Para obter essa expressão, devemos realizar uma analise de algebra de blocos.
Perceba que a relação entre o sinal de realimentação B(s) e o sinal de erro
atuante E (s) é
FT de malha aberta =
1 of 42
B(s)
= G (s)H(s)
E (s)
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
A relação entre o sinal de saı́da Y (s) e o sinal de erro atuante é chamada de
função de transferência do ramo direto,
FT de ramo direto =
Y (s)
= G (s)
E (s)
A expressão que relaciona a saı́da Y (s) e a entrada R(s) é obtida como:
Y (s) = G (s)E (s)
E (s) = R(s) − B(s) = R(s) − Y (s)H(s)
Realizando-se a substituição, tem-se:
Y (s) = G (s) [R(s) − Y (s)H(s)]
Y (s) [1 + G (s)H(s)] = G (s)R(s)
Portanto, a função de transferência de malha fechada é dada por:
G (s)
Y (s)
=
R(s)
1 + G (s)H(s)
2 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Diagrama de Blocos
Os elementos de um diagrama de blocos são listados a seguir:
• Seta: representação do sentido do fluxo de sinal.
• Bloco: operação matemática sobre o sinal de entrada que produz a saı́da.
Normalmente uma função de transferência.
• Ponto de soma: cı́rculo com o sı́mbolo “+” que indica uma operação de
soma. O sinal do lado externo determina se é realizada soma ou subtração.
• Ponto de junção: ponto a partir do qual o sinal proveniente de um bloco
vai para outros blocos ou pontos de soma.
3 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Propriedades dos Diagramas de Blocos
Associação em Cascata (Série):
Associação em Paralelo:
Realimentação Negativa:
4 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
5 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
6 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Gráfico de Fluxo de Sinais
Consiste em uma rede na qual os nós são conectados por ramos direcionados.
Os nós correspondem às variáveis do sistema e um ramo relaciona as variáveis
de entrada e saı́da pela multiplicação por um ganho.
Definições Básicas
• Nó - ponto que representa uma variável.
• Transmitância - Ganho entre dois nós.
• Ramo - Segmento direcionado que conecta dois nós aplicando um ganho à
variável de entrada.
• Nó de entrada - Nó que tem somente ramos de saı́da.
• Nó de saı́da - Nó que tem somente ramos que chegam.
• Nó misto - Nó que possui ambos tipos de ramos.
• Caminho - Percurso através dos ramos.
• Malha - Caminho fechado.
• Malhas que não se tocam - aquelas que não possuem nós em comum.
• Caminho de avanço - Caminho que inicia em um nó de entrada e termina
em um de saı́da sem passar por nenhum nó mais do que uma vez.
7 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo
8 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Propriedades dos Gráficos de Fluxo de Sinais
9 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Representação de Sistemas Lineares
x1 = a11 x1 + a12 x2 + a13 x3 + b1 u1
x2 = a21 x1 + a22 x2 + a23 x3 + b2 u2
x3 = a31 x1 + a32 x2 + a33 x3
10 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Representação de Sistemas Lineares
11 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Fórmula de Ganho de Mason
P=
1 X
Pk ∆k
∆
k
Pk : ganho do caminho direto de ordem k
P
P
P
∆: determinante do gráfico ∆ = 1 − a La + b,c Lb Lc − d,e,f Ld Le Lf
(1 - soma dos ganhos das malhas + soma dos produtos dos ganhos das
combinações de duas malhas que não se tocam - mesma coisa para
combinações de três malhas + ...)
∆k : cofator do k-ésimo caminho direto do gráfico de onde foram removidas
todas as malhas que tocam esse caminho.
12 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo
Obtenha a função de transferência de malha fechada C(s)/R(s) usando a fórmula de ganho de Mason.
13 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo
Obtenha a função de transferência de malha fechada C(s)/R(s) usando a
fórmula de ganho de Mason.
14 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Homework
Obtenha a função de transferência de malha fechada C(s)/R(s) usando a
fórmula de ganho de Mason.
15 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Modelagem de Sistemas Elétricos
Algumas relações envolvendo componentes elétricos básicos:
16 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo (Função de Transferência)
Encontre a função de transferência Eo (s)/Ei (s) do seguinte circuito RLC:
Aplicando a lei da tensões de Kirchhoff e depois a transformada de Laplace
(com condições iniciais nulas), tem-se:
Z
Z
di(t)
1
1
L
+ Ri(t) +
i(t)dt = ei (t) e eo (t) =
i(t)dt
dt
C
C
1
I (s) = Ei (s)
LsI (s) + RI (s) +
Cs
1
Eo (s) =
I (s) ⇒ I (s) = CsEo (s)
Cs
17 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo (continuação)
Portanto,
LCs 2 Eo (s) + RCsEo (s) + Eo (s) = Ei (s)
1
Eo (s)
=
⇒
Ei (s)
LCs 2 + RCs + 1
Exemplo (Elementos em Cascata)
Eo (s)
1
=
Ei (s)
(R1 C1 s + 1)(R2 C2 s + 1) + R1 C2 s
18 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Para componentes conectados em série, a impedância total é a soma das
impedâncias das componentes.
Zequiv = Z1 + Z2 + . . . + Zn
Para componentes conectados em paralelo, a inversa da impedância total é
a soma das inversas das impedâncias das componentes.
1
1
1
1
=
+
+ ...+
Zequiv
Z1
Z2
Zn
19 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Impedância RC
• A impedância equivalente resultante de um R em série com C é
Zequiv = R +
1
sCR + 1
=
sC
sC
• A impedância equivalente resultante de um R em paralelo com C é
1
Zequiv
20 of 42
=
1
1 + sCR
+ sC =
R
R
⇒
Zequiv =
R
1 + sCR
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
+
Z1
+
Vo
Vi
−
−
Z2
A relação entrada-saı́da do circuito é dada por
Vo
Z2
=
Vi
Z1 + Z2
Homework
Elabore um circuito usando apenas resistores e capacitores de modo que
s +a
Vo (s)
=
Vi (s)
s +b
no qual a e b são constantes que dependem dos resistores e capacitores.
21 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Circuito lead [avanço de fase]
R1
Vi
C1
R2
Note que R1 e C1 em paralelo resulta em
Z1 =
No circuito temos Z2 = R2 .
22 of 42
R1
1 + R1 C1 s
Vo
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
R1
Vi
R2
C1
Vo
Fazendo as contas vemos que
s + R11C1
s +a
R2 (1 + R1 C1 s)
Z1
V0 (s)
=
=
=
=
Vi (s)
Z1 + Z2
R1 + R2 + R1 C1 s
s +b
s + R11C1 + R21C1
Portanto
a=
1
R1 C1
b=
Perceba que a < b. Calcule a fase de
sistema realiza avanço.
23 of 42
1
1
+
R1 C1
R2 C1
V0 (s)
Vi (s)
e conclua que a < b implica que o
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Circuito lag [atraso de fase]
Homework
Faça a análise do circuito de
modo a determinar a e b tal que
a>be
s +a
V0 (s)
=
Vi (s)
s +b
(s)
Calcule a fase de VV0i (s)
e conclua
que a > b implica que o sistema
realiza atraso.
1
e b = R21C2 .
Dica: a = (R1 +R
2 )C2
24 of 42
Vi
R1
R2
C2
Vo
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Circuito lead-lag
Homework
Faça a análise do circuito de modo
a determinar a1 < b1 e a2 > b2
(s + a1 )(s + a2 )
V0 (s)
=
Vi (s)
(s + b1 )(s + b2 )
Vi
R1
C1
Dica:
(s +
V0 (s)
=
1
Vi (s)
s 2 + R2 C2 +
25 of 42
1
R1 C1 )(s
+
1
R2 C1
1
R1 C1
+
1
R2 C2 )
+
1
R1 C1 R2 C2
R2
C2
Vo
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Elementos sem Carga em Cascata
• A função de transferência de dois sistemas sem carga em cascata é a
multiplicação das funções de transferência individuais.
• Essa abordagem considera que a impedância de entrada do segundo
sistema é infinita, senão for ocorre o chamado efeito de carga.
• Para evitar esse efeito, utilizam-se amplificadores de acoplamento
(amp-ops).
26 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Amplificadores Operacionais
• Impedância de entrada infinita
• Impedância de saı́da zero
• Alto ganho diferencial (K):
e0 = K (e2 − e1 )
Exemplo (Amplificador Inversor)
Encontre a função de transferência do circuito com amp-op configuração inversor.
27 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo (continuação)
Como a impedância de entrada é elevada, a corrente de entrada no amplificador
é extremamente pequena. Assim, a equação de correntes no nó n é:
Eo − En
Ei − En
+
=0
Z1
Z2
Como o ganho diferencial do amp-op é muito alto, En ≈ 0, portanto:
Eo
Ei
+
=0
Z1
Z2
Z2
Eo
=−
Ei
Z1
28 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo
Encontre a função de transferência do circuito com amp-op abaixo.
29 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Homework
Encontre a função de transferência de cada circuito.
30 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Modelagem de Sistemas Mecânicos
A tabela seguinte apresenta algumas relações envolvendo componentes mecânicos:
31 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo
Obtenha a função de transferência, X (s)/F (s), para o sistema abaixo.
Considerando que a massa está sendo deslocada para a direita, somente a
força aplicada aponta para a direita; todas as outras forças impdedem o
movimento e agem contra ele. O diagrama do corpo livre deste sistema é
dado por:
32 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo (continuação)
Logo,
dx(t)
d 2 x(t)
+b
+ Kx(t) = f (t)
dt 2
dt
Aplicando a transformada de Laplace, com condições iniciais nulas, tem-se:
M
Ms 2 X (s) + bsX (s) + KX (s) = F (s)
Portanto,
33 of 42
X (s)
1
=
2
F (s)
Ms + bs + K
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Sistemas Massa-Mola-Amortecedor
• u(t): entrada - deslocamento do carro (u̇(t) constante)
• y (t): saı́da - deslocamento da massa m
34 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Continuação
ma =
m
d 2y
= −b
dt 2
X
F
du
dy
−
dt
dt
− k(y − u)
Ou, equivalentemente:
m
dy
du
d 2y
+b
+ ky = b
+ ku
dt 2
dt
dt
Aplicando-se Laplace:
ms 2 + bs + k Y (s) = (bs + k) U(s)
Y (s)
bs + k
=
U(s)
ms 2 + bs + k
35 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Sistemas Massa-Mola-Amortecedor Acoplados
m1 ẍ1 = −k1 x1 − k2 (x1 − x2 ) − b(ẋ1 − x˙2 ) + u
m2 ẍ2 = −k3 x2 − k2 (x2 − x1 ) − b(ẋ2 − x˙1 )
36 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Continuação
m1 ẍ1 + bẋ1 + (k1 + k2 )x1 = k2 x2 + bx˙2 + u
m2 ẍ2 + bẋ2 + (k2 + k3 )x2 = k2 x1 + bx˙1
Aplicando-se Laplace:
m1 s 2 + bs + (k1 + k2 ) X1 (s) = (k2 + bs) X2 (s) + U(s)
Resolvendo-se:
m2 s 2 + bs + (k2 + k3 ) X2 (s) = (k2 + bs) X1 (s)
X1 (s)
m2 s 2 + bs + k2 + k3
=
U(s)
(m1 s 2 + bs + k1 + k2 )(m2 s 2 + bs + k2 + k3 ) − (bs + k2 )2
37 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Modelagem de Sistemas Mecânicos Rotativos
Função de Transferência de Circuitos Mecânicos Rotativos
38 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo (Modelagem de Servomotor de Corrente Contı́nua)
Os servomotores DC têm diversas caracterı́sticas interessantes como controlabilidade, portabilidade, baixos custos de aquisicão e manutenção e adaptabilidade
a vários tipos de sistemas de controle. Considera-se a modelagem do servomotor controlado por armadura (campo constante).
39 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo (Continuação)
Assumindo corrente de campo (if ) constante, o torque do motor é proporcional
à corrente de armadura:
Tm (s) = Km Ia (s)
O torque do motor é igual à soma do torque da carga (Js 2 θ(s) + bsθ(s)) e o
torque de distúrbio, Td (s). Considerando Td (s) = 0, tem-se:
Tm (s) = Km Ia (s) = Js 2 θ(s) + bsθ(s)
A corrente de armadura se relaciona com a tensão de armadura como:
Va (s) = (Ra + La s) Ia (s) + Vb (s),
onde Vb (s) é a TL da força controeletromotriz gerada, que é proporcional à
velocidade do motor, ou seja,
Vb (s) = Kb ω(s)
40 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo (Continuação)
Assim, a corrente da armadura pode então ser escrita como:
Ia (s) =
Va (s) − Kb ω(s)
R a + La s
Então, tem-se:
Km Va (s) − Km Kb ω(s)
= s (Js + b) θ(s),
R a + La s
que pode ser escrita como (note que ω(s) = s θ(s))
Km Va (s) = s [(Js + b) (Ra + La s) + Km Kb ] θ(s).
Assim, a função de transferência θ(s)/Va (s) é dada por:
Km
θ(s)
=
Va (s)
s [(Js + b) (Ra + La s) + Km Kb ]
41 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Exemplo (Continuação)
Como ω(s) = s θ(s), a função de transferência ω(s)/Va (s) é dada por:
Km
ω(s)
=
Va (s)
(Js + b) (Ra + La s) + Km Kb
O diagrama de blocos do modelo motor controlado por armadura é dado por:
42 of 42
B. A. Angelico, P. R. Scalassara, A. N. Vargas, UTFPR, Brasil
Dica de atividades
Dica
1. Fazer os Exercı́cios apresentados no Cap. 9 do livro “Sistemas de Controle
Modernos” - Richard C. Dorf, Robert H. Bishop.
2. Fazer os Exercı́cios apresentados no livro K. OGATA, “Engenharia de
Controle Moderno”.
43 of 42