Integrais de Linha Intervalares: Fundamentos e Aplicações

Giovani Ângelo Silva da Nóbrega
Integrais de Linha Intervalares:
Fundamentos e Aplicações
Natal RN
Maio / 2010
Giovani Ângelo Silva da Nóbrega
Integrais de Linha Intervalares:
Fundamentos e Aplicações
Dissertação
apresentada
como
requisito
para aprovação na disciplina Dissertação de
Mestrado no período 2010.1.
Orientador:
Prof. Dr. Benjamin Rene Callejas Bedregal
Co-orientador:
Prof. Dr. Roberto Callejas Bedregal
Grupo de Lógica, Linguagem Informal, Teoria e Aplicação LoLITA
Programa de Pós-Graduação em Sistemas e Teoria da Computação
Departamento de Informática e Matemática Aplicada
Centro de Ciências Exatas e da Terra
Universidade Federal do Rio Grande do Norte
Natal RN
Maio / 2010
Dedico este trabalho aos meus pais, quem sempre me apoiaram e me forneceram
toda a educação necessária.
Agradecimentos
Primeiramente agradeço a Deus por toda a força e inteligência concedida, além de
ter guiado os meus passos.
Segundo, este trabalho não teria sido feito sem a ajuda
de diversas pessoas com quem convivo.
Agradeço à minha família que sempre me
apoiou. Agradeço a todos os professores da minha graduação e pós-graduação, em especial àqueles que me ensinaram e orientaram sobre matemática e teoria da computação.
E especialmente ao professor Benjamin Rene Callejas Bedregal pela paciência, incentivo
e pelo exemplo de competência e humanidade. Agradeço ao professor Enivaldo Bonelli
pela paciência, amizade e pelas aulas informais sobre física e matemática.
Resumo
A necessidade de uma precisão e de uma aproximação dos resultados numéricos
zeram com que diversas teorias surgissem: dentre elas, destacamos a Matemática Intervalar. A Matemática Intervalar surgiu na década de 60 com os trabalhos de pesquisa
de Moore (MOORE, 1959) , em que ele propôs trabalhar com uma Matemática baseada
na noção de intervalo real e não mais com um número como aproximação. Com isso,
surgiu a necessidade de revisitar e reformular os conceitos e resultados da Matemática
Clássica utilizando como base a noção de intervalo de Moore. Uma das áreas da Matemática Clássica que tem tido muitas aplicações em engenharias e ciências é a Análises
Numérica, onde um dos seus pilares é o Cálculo Integral e em particular as integrais de
linha. Assim, é muito desejável se ter um cálculo integral dentro da própria Matemática
Intervalar.
No presente trabalho apresenta-se uma noção de Integral de Linha Intervalar baseada na extensão de integração proposta por Bedregal em (BEDREGAL; BEDREGAL,
2010). Para a fundamentação apresenta-se incialmente uma introdução sobre a pespectiva em que o trabalho foi realizado, considerando alguns aspectos histórico-evolutivos
da Matemática Clássica. Os conceitos de Integrais de Linha Clássica, bem como algumas das suas aplicações mais importantes. Alguns conceitos de Matemática Intervalar
necessários para o entendimento do trabalho. Para nalizar propomos uma aplicação
da integral de linha em um experimênto clássico da mecânica quântica (a difração de
um elétron em uma fenda) que graças ao fato de ser a Matemática Intervalar utilizada,
nos dá um foco mais detalhado e mais próximo da realidade.
Palavras-chave:
Matemática Aplicada.
Matemática Intervalar, Análise Intervalar, Integral de Linha e
Abstract
The requirement of a greater precision and approximation of numerical results gave
rise to various theories: among them, we can highlight the mathematics of intervals.
The mathematics of intervals appeared in the 60s with the research works by Moore, in
which he proposed to work with mathematics based on the notion of real interval instead
of pointed numbers. So, a necessity of revisiting and reformulating the concepts and
results of classic mathematics appeared, using Moore's notion of intervals as basis. One
of the elds in classic mathematics which has had plenty of application in engineering
and sciences is the numerical analysis, whose one important basis is the full dierential
calculus and, in particular, the line integrals. Therefore, it is really desirable to have a
dierential and full calculus inside the mathematics of intervals itself. However, scientic work reasonably based in such theory cannot be found in the literature, that means,
works which contain a notion of integrals and derivatives for functions of interval that
fulll a similar result to the fundamental calculus theorem. This work presents a notion
of integral of line of intervals based on the integration extension proposed by Bedregal.
As fundamentals, this work presents, at rst, an introduction about the perspective
adopted by it, considering some historical-evolutionary aspects of classic mathematics.
The classical concepts of integrals of line, as well as some of their most important applications. Finally, an application of a line of integral in a classical experiment on quantum
mechanics (a diraction of an electron into a crack) is proposed, which, due to the fact
of the usage of the mathematics of intervals, provides a more detailed focus, closer to
reality.
Sumário
Lista de Figuras
Lista de Símbolos
1 Introdução
p. 11
1.1
Cálculo Integral Clássico . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 12
1.2
Cálculo Integral Intervalar . . . . . . . . . . . . . . . . . . . . . . . . .
p. 13
2 Integral de Linha Clássica
p. 15
2.1
Caracterização da Integral de Linha
. . . . . . . . . . . . . . . . . . .
p. 15
2.2
Propriedades de Integrais de Linha . . . . . . . . . . . . . . . . . . . .
p. 17
2.3
Aplicações de Integrais de Linha
. . . . . . . . . . . . . . . . . . . . .
p. 18
2.3.1
Densidade Linear . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 18
2.3.2
Lei de Biot-Savart
. . . . . . . . . . . . . . . . . . . . . . . . .
p. 18
2.3.3
Mercado Financeiro
. . . . . . . . . . . . . . . . . . . . . . . .
p. 19
3 Fundamentos de Matemática Intervalar
p. 22
3.1
Conceitos fundamentais
. . . . . . . . . . . . . . . . . . . . . . . . . .
p. 22
3.2
Propriedades Algébricas . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 24
3.3
Relação de Ordem
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 24
3.4
Topologia no I R
( )
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 25
3.5
Integração Intervalar . . . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 28
3.5.1
Integral de Moore e Yang
. . . . . . . . . . . . . . . . . . . . .
p. 28
3.5.2
Integral de Bedregal-Bedregal . . . . . . . . . . . . . . . . . . .
p. 29
4 Integral de Linha Intervalar
p. 30
5 Aplicação da Integral Intervalar de Linha Intervalar
p. 39
5.1
Difração de uma Partícula . . . . . . . . . . . . . . . . . . . . . . . . .
p. 40
5.2
Experimento
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 41
5.3
Modelagem Intervalar do Experimento de Difração de uma Partícula .
p. 43
5.3.1
p. 53
Considerações Finais sobre o Experimento . . . . . . . . . . . .
6 Conclusões e Trabalhos Futuros
6.1
Conclusões
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2
Trabalhos Futuros
Referências Bibliográcas
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 55
p. 55
p. 56
p. 57
Lista de Figuras
2.1
Variação dos índices Dow Jones . . . . . . . . . . . . . . . . . . . . . .
p. 20
5.1
Modelo de Difração . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
p. 42
5.2
Modelo da Difração Intervalar . . . . . . . . . . . . . . . . . . . . . . .
p. 43
5.3
Representação geométrica dos átomos e suas distâncias . . . . . . . . .
p. 44
5.4
Força gerada pelo campo elétrico da fenda . . . . . . . . . . . . . . . .
p. 47
5.5
Função força intervalar resultante . . . . . . . . . . . . . . . . . . . . .
p. 49
5.6
Gráco do Trabalho do
Movimento 1
. . . . . . . . . . . . . . . . . .
p. 52
5.7
Gráco do Trabalho do
Movimento 2
. . . . . . . . . . . . . . . . . .
p. 53
Lista de Símbolos
I
intervalo real
P (I )
conjunto de partições do intervalo
P
I (R)
I
diam(A)
A
d
A
F
j j
kk
max(X)
min(X)
Dom(f)
(F;; P )
(F;; P )
B
A F(X)dX
F(X)dS
k(t)k
P
R
R
I
Partição
Subconjunto aberto do R
n
Extensão dos reais intervalar
Subconjunto de intervalos de IR
Distância dos extremos do intervalo
Supremo de A
Inmo de A
Operador de módulo
Operador de norma
Valor máximo real do conjunto X
Valor mínimo real do conjunto X
Domínio da função
f
Somatório inferior de Riemann
Somatório superior de Riemann
Integral intervalar de F
Integral de Linha Intervalar de F sobre
Norma da função
11
1 Introdução
A computação cientíca tem ganho cada vez mais espaço no meio ciêntico, isso
por apresentar resultados cada vez mais rápidos e eciêntes no processamento de informações numéricas.
Junto a esse ganho de espaço no meio cientíco veio também
a necessidade do conhecimento e do controle rigoroso dos erros gerados e acumulados
durante o processamento dos dados. Existem, basicamente, três tipos de erros previstos
na computação: o primeiro tipo de erro é aquele oriundo das falhas ou incapacidade de
medição dos dados de entrada, devido a não serem erros da computação não é possível
torná-los sucientemente pequenos.
onados ao
arredondamento
e
O segundo e terceiro tipo de erros são os relaci-
truncamento.
O erro de arredondamento consiste na
aproximação de números reais para um número nito de dígitos, já o erro de truncamento surge do truncamento de um processo iterativo onde uma sequência innita de
operações aritméticas deve ser parada após um número nito de etapas. Tanto o erro
de arrendondamento quanto o erro de trucamento podem ser controlados a partir de
processos computacionais rigorosos, porém de custo computacional elevado.
No nal
da década de 50, os trabalhos (MOORE; YANG, 1959) e (SUNAGA, 1958) apresentam uma aritmética baseada em intervalos de extremos reais que tem como objetivo
mostrar uma solução segura e conável para problemas que não têm uma entrada de
dados exatos; não têm uma representação nita na linguagem de máquina, que possam
causar erros de truncamento ou arredondamento durante as interações; e que possibilita o controle automático dos erros da computação numérica.
Desde então, diversos
trabalhos tem sido desenvolvidos no intuito de dar uma maior fundamentação a esta
teoria assim como mostrar aplicações bem sucedidas da mesma em várias áreas, em que
destacamos: na física (CHANG; YU; LIOU, 1993), na engenharia (MERLET, 2004),
na robótica (ASHOKARAJ et al., 2004), na teoria de circuitos (KOLEV, 1993) e na
própria matemática (MENDOZA et al., 2009).
Mas a evolução da análise intervalar
1.1 Cálculo Integral Clássico
12
esbarra em alguns problemas que, segundo (TRINDADE, 2009), estão concentrados na
escolha da topologia para a denição dos espaços intervalares. Contudo, mesmo com
esses problemas, algumas teorias da matemática clássica tem sido estendidas para a matemática intervalar, porém, no caso da integral de linha não encontramos na literatura
qualquer extensão intervalar da mesma. Este trabalho tem como objetivo desenvolver
tal extensão de forma matematicamente fundamentada.
1.1
Cálculo Integral Clássico
Segundo (BOYER, 1949), o primeiro indício do cálculo integral foi encontrada no
Papiro Egípcio de Moscow datado de 1.800 a.C. que consistia, basicamente, em um
método não formal de cálculo de volume e área das pirâmides.
evolução da integração foi o surgimento do
método de exaustão
Um outro marco na
creditado a Eudoxo,
pelo qual se aproxima a quantidade desejada pelas somas parciais de uma série ou pelos
termos de uma sequência. Arquimedes (287-212 a.C.) com o seu trabalho mostrou um
modelo heurístico do método de exaustão desenvolvido por Eudoxo. Apesar do grande
progresso que o cálculo diferencial e integral ganhou entre os séculos XVI e XVII com
as contribuições dos grandes estudiosos da época, como Newton, Leibniz e Euler uma
fundamentação rigorosa só veio surgir no século XVIII com os trabalhos da época que,
dos quais destacamos os de Cauchy, Riemann e Weierstrass pelo estudo analítico das teorias matemáticas até então criadas. Destacamos o trabalho de Riemann sobre integrais
que se tornou importânte na história, segundo (BOYER, 1949), devido a ser a primeira
denição formal da integração de uma função denida em um intervalo.
Apesar da
denição de Riemann não ser uma formalização denitiva sobre integração, ela serviu
de base para o desenvolvimento das integrais de Riemann-Stieltjes que, posteriormente,
veio a ser estendida por Lebesgue para o que conhecemos como as integrais de Lebesgue.
Ainda nesse período, os estudos feitos na análise complexa tiveram resultados
fundamentais para a consolidação de teorias que até então não haviam sido vericadas
de forma analítica.
Destacamos a denição da integração no conjunto dos números
complexos que, também, foi denida no conjunto dos reais com o nome de
linha
integral de
que consiste em uma generalização das integrais denidas. A generalização das
integrais denidas possibilitou aplicações diversas onde destamos a aplicação no proces-
1.2 Cálculo Integral Intervalar
13
samento digital de imagens (SUNDQUIST, 2003); na física quântica, na estatística e na
matemática nanceira (KLEINERT, 2004).
1.2
Cálculo Integral Intervalar
Com o sucesso da matemática intervalar, naturalmente, reproduzir as teorias construidas na matemática clássica para a matemática intervalar veio a ser um dos principais
focos dos pesquisadores da área. O cálculo integral foi uma dessas teorias, onde destacamos o trabalho (SUNAGA, 1958) que apresenta a utilização do Método de Simpson
1
com o ajuste do erro baseado nas operações em intervalos. Já em (MOORE; YANG,
1959) foi apresentado uma fundamentação teórica do que seria uma integração intervalar de uma função intervalar.
O trabalho (ACIOLY, 1991) apresenta uma integração
de funções intervalares denidas sob a topologia de Scott.
Encontra-se no trabalho
(BEDREGAL; BEDREGAL, 2010) a fundamentação de um novo modelo de integração
que pode ser denido entre intervalos, diferentemente da integral de Moore que era
denida entre números reais. Sob a luz dessa evolução propomos no presente trabalho
uma fundamentação de um modelo de integral de linha intervalar como uma extensão
da integral proposta em (BEDREGAL; BEDREGAL, 2010).
Assim, este trabalho se encontra estruturado nos seguintes capítulos:
O capítulo 2, apresenta um resumo sobre as integrais de linha clássicas, a saber: a
denição, o teorema de caracterização, algumas das principais propriedades e aplicações.
O capítulo 3, apresenta um estudo das principais propriedades e aritmética inter-
( )
integrações intervalares e relações de pré-ordem no conjunto I(R).
valar básica (operações básicas); a topologia de Moore no I R ; funções intervalares,
O capítulo 4, desenvolve a proposta da dissertação. Apresentamos a denição e a
fundamentação de uma integral de linha baseada na integral fundamentada em (BEDREGAL; BEDREGAL, 2010).
O capítulo 5, apresenta um experimento clássico da mecânica quântica, a difração de
elétron em uma fenda. Neste experimento passamos a considerar uma das coordenadas
1 método
numérico utilizado para o cálculo de integrais denidas
1.2 Cálculo Integral Intervalar
14
da posição relativa do elétron como um intervalo e com isso, foi possível considerar
outras variáveis que até então não estavam inseridas no escopo do problema. Assim é
possível calcular o trabalho, usando a integral de linha intervalar, realizado pelas forças
durante a trajetória da partícula durante o experimento.
15
2 Integral de Linha Clássica
Intuitivamente podemos pensar em um caminho como um lugar geométrico, ou
seja, como um conjunto de pontos com uma determinada propriedade.
Também é
bem possível pensar no caminho como uma trajetória de uma partícula em movimento
em que as coordenadas são funções de um parâmetro que é regido pelo tempo. Esta
abordagem é a mais usada, pois usa como linguagem as funções que permitem explorar
melhor as características do caminho.
2.1
Caracterização da Integral de Linha
Denição 2.1. Uma partição de um intervalo real I = [a;b] é uma sequência P =
fa = x0;x1;:::;xn = bg tal que para cada i = 0;:::;n 1, xi < xi+1. P(I) é o conjunto
das partições de I .
Denição 2.2. A partição P1 de
por P1 P2 , se P2 P1 .
I é mais na que a partição P2 de I , denotada
Denição 2.3. Um caminho em um aberto Rn é uma aplicação : I
domínio é um intervalo I R.
! cujo
: I ! Rn é diferenciável em todos os ponto de I dizemos que o
0
n
caminho é diferenciável em I . A derivada nos dá uma aplicação : I ! R . Quando
0
1
a aplicação é contínua dizemos que é de classe C
Denição 2.4. Seja f : [a;b] ! um caminho com imagem denida no aberto
R, isto é, uma aplicação cujo domínio é um intervalo da reta. Diz-se que o
caminho f : [a;b] ! é diferenciável no ponto t0 2 [a;b] se existe:
f(t+h) f(t)
f 0(t0) = hlim
!0
h
Quando o caminho
2.1 Caracterização da Integral de Linha
16
chamado a derivada de f no ponto t0 .
Denição 2.5. Seja a função f : Rn ! R e o caminho
de linha de f sob o caminho é denida como
Z
Onde dS
: I ! , a integral
m
X
fdS = lim
f((ti))(ti)
!0
=0
é o comprimento innitesimal do caminho gerado pelo caminho .
i
Teorema 2.1. (FULKS, 1969) Considere uma função f : Rn ! R denida no
aberto . Tomemos uma função : [a;b] ! como uma função caminho. Então
Z
Z
0
fdS
=
f((t))
k
(t)kdt
a
b
P = fa = t0 < t1 < t2 < t3 < ::: < tm = bg de
0
0
0
0
0
0
um intervalo I , onde qualquer partição P = fa = t0 < t1 < t2 < t3 < ::: < tk = bg que
0
satisfaça P P . Claramente se verica que
Demonstração.
Considere uma partição
m
X
=0
i
k
X
f((ti))k(ti) (ti 1)k 6 f((t0i))k(t0i) (t0i 1)k
=0
i
Sabendo que a função é contínua:
k 0(t) 0(ti)k 6 "
Onde
8t 2 [ti 1;ti];i = 0;1;:::;m
" é uma constante relativamente pequena, Então:
m
X
=0
i
Mas
f((ti))k(ti) (ti 1)k = f((t))
Z ti
t
i
E
Z ti
t
i
m
X
=0
i
1
1
0(ti)dt
Z ti
t
i
0(t)dt 6 Z
1
ti
ti
1
Z ti
t
( 0(t) 0(ti))dt 6
0(ti)dt + Z
ti
ti
1
i
1
Z ti
t
( 0(t)
i
0(t)dt
1
0(t)dt
0(ti))dt
Além disso
Z ti
t
i
1
( 0(t)
0(ti))dt 6
Z
ti
ti
1
k( 0(t) 0(ti))kdt 6 "(ti ti 1)
2.2 Propriedades de Integrais de Linha
17
Logo
m
X
=0
i
m
X
f((ti))k(ti) (ti 1)k 6 (f((ti))k 0(ti)k(ti ti 1)+"(ti ti 1)) 6
=0
i
U (f((t))k 0k;P)+f((t))"(b a)
m
X
=0
i
m
X
f((ti))k(ti) (ti 1)k > (f((ti))k 0(ti)k(ti ti 1) "(ti ti 1)) >
=0
i
L(f((t))k 0k;P) f((t))"(b a)
Tomando partições arbitrariamente nas, conclui-se que:
Z
b
Z
b
Z
b
f((t))k 0(t)kdt f((t))"(b a) 6 a f((t))k 0(t)kdt
a
e
Z
b
f((t))k 0(t)kdt 6 a f((t))k 0(t)kdt+f((t))"(b a)
a
Sendo um
2.2
" sucientemente pequeno.
Propriedades de Integrais de Linha
Proposição 2.1. Seja f : Rn ! R e g : Rn ! R funções denidas no
aberto , : [a;b] ! a função que descreve o movimento de uma partícula em
medido em t.
1. Se a e b são números reais quaisquer tem-se
Z
Z
Z
(af +bg)dS = a fdS +b gdS
2. Se a curva é de class C 1 por partes, se for contínua e se existirem uma
partição a = t0 < t1 < ::: < tn = b e curvas i : [ti 1 ;ti ] ! , i = 1;2;3;4;:::;n,
de classe C 1 .
Z
Z
Z
Z
fdS = fdS + fdS +:::+ fdS
1
2
n
2.3 Aplicações de Integrais de Linha
2.3
2.3.1
18
Aplicações de Integrais de Linha
Densidade Linear
A integral de linha, relativa ao comprimento de arco, pode ser aplicada no cálculo da
massa de um o delgado, cuja
densidade linear seja conhecida de alguma maneira (valor
escalar ou alguma função com os parâmetros de entradas conhecidas ou estipuláveis).
Sendo assim: Dado a função
função
: [a;b] ! Rn, que representa a forma do o, e a
: Rn ! R a função densidade do o, a massa é dada for:
Z
2.3.2
Z
b
dS = a ((t))k 0(t)kdt
Lei de Biot-Savart
Dada uma carga positiva
q, movendo-se a uma velocidade !v .
Essa carga em mo-
vimento origina um campo magnético, cuja a intensidade em um ponto
P
qualquer é
dada por:
Bq = k q vrsen()
2
!!
onde, r é a distância entre a carga e P , e é o ângulo formado entre v , r e k é a
Nm
constante eletrostática no vácuo de valor 8;988 109
C
2
2
Suponha que a corrente elétrica de intensidade
i
circula um condutor em forma de
2.3 Aplicações de Integrais de Linha
19
C . Dividindo o condutor em pequenos segmentos de dimensão ds e admitindo
que a área de sua seção reta é A, podemos dizer que o volume pode ser calculado por
Ads. Sendo, n portadores de carga para cada unidade de volume e cada um de carga
q, então a carga total é:
dQ = n q A ds
(2.1)
O conjunto de cargas em movimento é equivalente a uma única carga dQ, movendo em
!
!
velocidade v , logo em um ponto qualquer P , o campo magnético d B produzido pelas
cargas de intensidade dB dada por:
dB = k dQ vr2sen()
(2.2)
uma curva
Substituindo a equação 2.1 em 2.2 teremos
dB = k n q v Ar2ds sen()
e sendo
n q v A a intensidade da corrente i, deste modo:
dB = k i dsrsen()
2
(2.3)
(2.4)
Lei de Biot-Savart. Ela fornece a intensidade do
campo magnético B gerado pela corrente i em qualquer ponto da curva de comprimento
A expressão 2.4 é conhecida como
ds. A intensidade do campo magnético resultante !
B em um ponto P qualquer é dado
pela integral de linha.
2.3.3
B = k C i sen()
r2 ds
Z
Mercado Financeiro
Um importante campo de aplicação da integral de linha é o mercado nanceiro. Os
preços do mercado nanceiro utuam em função do tempo, e quanto maior o número
de participantes no mercado, maior é a variação do valor utuante, podendo chegar
a ter um carater estocástico.
Esse comportamento aleatório é melhor interpretado,
sob o ponto de vista matemático, quando utilizamos sistemas de equações diferenciais
estocásticas, que para seus estudos, as integrais de linha ( como integrais de caminho)
são fundamentais para resolução desses sistemas. No texto desta seção, mostraremos
o desenvolver de uma dessas conclusões que é importante para o processamentos de
2.3 Aplicações de Integrais de Linha
20
informações pertinentes ao mercado.
Flutuação de Propriedades dos Valores Financeiros
Seja
S(t) o estoque monetário de uma ação ou outro valor nanceiro.
Analisando
a média dos preços das ações (ou de algum valor monetário) em longos períodos de
tempo, segundo (DOROGOVTSEV, 1995), pode ser aproximado exponencialmente isso
porque geralmente é utilizada uma escala exponencial para a plotagem. Isto é melhor
representado em 2.1.
Figura 2.1: Gráco do crescimento dos índices calculados sobre grandes unidades
industriais nos Estados Unidos nos últimos 60 anos
O estoque monetário satisfaz a equação diferencial estocástica para o crescimento
exponencial.
Onde
S 0(t) = rs +(t)
S(t)
S0 t
S t é chamado de
()
()
(2.5)
valor de retorno, rs , é a taxa de crescimento e (t) é o
ruido branco denido pela correlação da função:
h(t)i = 0
Onde
h(t)0(t)i = 2(t t0)
(2.6)
2 representa a variância dos valores. Muitas vezes é descrito como uma relação
2.3 Aplicações de Integrais de Linha
da volatilidade do preço das ações
21
v = . O retorno diário é calculado como:
S(t) = [S(tn+1) S(tn)]
O conjunto de todos os valores de
S(tn) é chamado de série de preços pelo tempo. Devido
aos valores serem muito grandes, faremos o logaritmo da equação
valor de retorno,
x(t) logS(t)
daí podemos escrever a equação diferencial de crescimento como:
0
x0(t) = SS 12 2 = rx +(t)
Daí tiramos que
rx rs 12 2
A diferenciação nita de x(tn ) = x(tn+1 )
x(tn) que corresponde a diferenciação dx
está relacionada ao retorno S(t) contudo é uma variação do logS(t). Contudo pela
expansão da derivada podemos ter:
dx dS(t)
dx = dS
0 (t)
dt
dx = SS(t)
1 d2x dS 2(t)+:::
2 dS 2 2
1 S 0(t) dt+:::
2 S(t)
"
#
As potências de ordem muito elevada não informam sobre a oscilação da potência gaussiana. Isso nos faz dizer que:
"
S 0(t) 2 dt = x02(t)dt
S(t)
#
Logo, é possível denir a média do estoque monetário em um período de tempo determinado pela integral de linha,
1
Z
b
0
b a a kx (t)kdt:
Que, em termos de aplicação a economia,fornece um indicador de desenvolvimento e
estabilidade econômica.
22
3 Fundamentos de Matemática
Intervalar
Apresentaremos neste capítulo alguns conceitos e denições básicas da matemática
intervalar que serão a base para o desenvolvimento dos lemas, teoremas, proposições
e corolários que serão apresentados no capítulo 4. Este capítulo está baseado nos trabalhos de (SUNAGA, 1958), (MOORE, 1959), (MOORE, 1966), (MOORE, 1979) e
(BEDREGAL; BEDREGAL, 2010).
3.1
Conceitos fundamentais
Denição 3.1. Dizemos que um intervalo é um conjunto fechado de números reais
representado pelo par composto pelo limite inferior e o limite superior do intervalo.
Assim para todo a;b 2 R tal que a b, o par [a;b] representa o intervalo.
[a;b] = fx 2 R j a 6 x 6 bg
(3.1)
a = b o intervalo [a;b] recebe o nome de intervalo
degenerado. O conjunto dos intervalos de extremos reais R é denominado de I(R).
Quando tivermos o caso de
Denição 3.2. O conjunto
( ) tem associado duas projeções:
I R
1;2 : I(R) ! R
1([x;x]) 7! x
2([x;x]) 7! x
Por convenção, para todo
por
x e x, respectivamente.
X 2 I(R), denotaremos suas projeções, 1(X) e 2(X),
3.1 Conceitos fundamentais
23
Denição 3.3 (Igualdade entre Intervalos). Sejam
Diz-se que X = Y se, e somente se x = y e x = y.
XeY
Denição 3.4 (Adição). Sejam X;Y 2 I(R). A soma de
X +Y , é o conjunto fx+y j x 2 X e y 2 Y g
dois intervalos de
X
( ).
I R
com Y , denotada por
X +Y = [x+y;x+y].
Denição 3.5 (Pseudo Inverso Aditivo). Dado X = [x;x] 2 I(R). X = [ x; x] 2 I(R)
é chamado de pseudo inverso aditivo de X . Observe que X = f x j x 2 X g
Sunaga em (SUNAGA, 1958) provou que
O pseudo inverso aditivo não é o inverso aditivo, pois a soma do pseudo inverso
[0;0] (que seria o intervalo neutro da soma). Pois, seja
X = [0;a] : para todo a 2 R f0g, logo o seu pseudo inverso seria X = [ a;0] portanto
X +( X) = [ a;a] 6= [0;0]. No entanto, podemos armar que 0 2 X X
Denição 3.6 (Subtração). Sejam X; Y 2 I(R). A subtração de Y em X , denotada
por X Y , é o conjunto fx y j x 2 X e y 2 Y g
com o intervalo nem sempre é
É fácil ver que pela denição de
portanto
pseudo inverso aditivo que
X Y = [x y;x y] = X +( Y ).
Y = [y;y] = [ y; y]
Este resultado foi devidamente provado
por Sunaga (SUNAGA, 1958)
Denição 3.7 (Multiplicação). Sejam X; Y 2 I(R). A multiplicação de
denotada por X Y , é o conjunto fx y j x 2 X e y 2 Y g
Sunaga em (SUNAGA, 1958) prova que
y;x y;x y;x y)]
X e Y,
X Y = [min(x y;x y;x y;x y);max(x Denição 3.8 (Pseudo Inverso Multiplicativo). Sejam o intervalo X . O pseudo
n
o
inverso multiplicativo de X é dado por X1 = x1 j x 2 X . Pelo fato de X1 =
n
1 j x 2 X o, 0 2= X .
x
Note que
1
X
= x1 ; x1 .
h
i
Denição 3.9 (Divisão). Seja os intervalos X e Y . A divisão de X por Y , denotada
n
o
n
o
por XY , é dada por XY = xy j x 2 X e y 2 Y Pelo fato de XY = x y1 j x 2 X e y 2 Y ,
zero não pode pertencer a Y .
X
Note que
Y
=
x 1
n
y
j x2X e y2Y =X
o
1; 1
y y .
3.2 Propriedades Algébricas
3.2
24
Propriedades Algébricas
As propriedades algébricas da aritmética intervalar são consequências imediatas do
conjunto de denições das operações da aritmética intervalar.
Proposição 3.1. Seja X,Y e Z
Associatividade na adição:
2 I(R), vale:
X +(Y +Z) = (X +Y )+Z
Associatividade na multiplicação:
Comutatividade na adição:
X (Y Z) = (X Y ) Z
X +Y = Y +X
Comutatividade na multiplicação
X Y = Y X
Identidade na adição: Existe 0 = [0;0] em
( ) tal que 0 +X = X + 0 = X
I R
Identidade na multiplicação: Existe 1 = [1;1] em
Subdistributividade:
Demonstração.
3.3
( ) tal que 1 X = X 1 = X
I R
X (Y +Z) X Y +X Z
Veja (MOORE, 1959)
Relação de Ordem
( )
Os intervalos em I R , podem assumir diversas semânticas diferentes. Um intervalo
pode ser visto como conjunto; como um intervalo; como uma informação; como uma
representação ou como um par ordenado.
É possível denir diversas ordens naturais
( ) respeitando uma semântica sobre I(R) .
sobre o conjunto I R
Denição 3.10 (Ordem de inclusão, (MOORE, 1979)). Sejam os intervalos X e Y a
ordem da Inclusão dene que X Y , y x e x y.
Denição 3.11 (Quase-ordem de Moore, (MOORE, 1979)). Sejam os intervalos X e
Y a ordem da Moore diz que X <M Y , 8x 2 X e 8y 2 Y;x < y , x < y.
Observe que a quase-ordem
1 de Moore não é uma ordem2 , pois não satisfaz a ree-
xividade.
1É
2É
uma relação que possui as propriedades: anti-reexiva e transitiva
uma relação que possui as propriedades: reexiva, anti-simétrica e transitiva
3.4 Topologia no
25
I(R)
Denição 3.12 (Ordem de Kulisch-Miranker, (KULISCH; MIRANKER, 1986)). Sejam
os intervalos X e Y a ordem de Kulisch-Miranker diz que X K Y , x y e x y.
Proposição 3.2 (Inclusão Monotônica, (MOORE, 1966)). Sejam X;Y;Z;W intervalos, tais que X Z e Y W . Então as seguintes relações são válidas:
ˆ
ˆ
ˆ
X +Y W +Z
X Z
X Y Z W
X Y Z W
1 1 desde que 0 2= Z;X
ˆ
X Z
X Z desde que 0 2= W;Y
ˆ
Y W
ˆ
Demonstração.
A prova é uma consequência direta das operações aritméticas.
Denição 3.13 (Ordem da Informação, (ACIOLY, 1991)). Sejam os intervalos
Y a ordem da informação diz que X v Y , X Y , x x e y y.
3.4
Topologia no
Xe
I(R)
Apresentamos nessa seção, algumas propriedades ligadas aos estudos de Análise
Intervalar como a noção de conjunto, partição, métrica e espaço métrico.
Denição 3.14. Uma partição de C 2 I(R) é uma sequência P = fc =x0 ;x1 ;x2 ;:::;xn =cg.
Tal que para cada i = 0;1;:::;n 1, xi < xi+1 . P(C) é o conjunto das partições de
C
Denição 3.15. A partição P1 de C é mais na que a partição P2 de C , denotada
por P1 4 P2 , se P2 P1
Proposição 3.3. Seja
(fc;cg).
Demonstração.
C 2 I(R). hP(C); 4i, é um reticulado com maior elemento
Veja em (BEDREGAL; BEDREGAL, 2010)
3.4 Topologia no
26
I(R)
Denição 3.16. Sejam
nimos
A e B dois intervalos reais distintos tal que A k B . DeI[A;B] = fX 2 I(R)j A k X k B g
(3.2)
Denição 3.17 (Distância entre dois intervalos). Sejam X;Y 2 I(R). A distância
entre X e Y , denotado por dM (X;Y ), é dada pelo número real não negativo
dM (X;Y ) = maxfjb aj; jb ajg
Proposição 3.4. Seja I um subconjunto não vazio de I(R). A função dM : I I
R+ é uma métrica de I pois satisfaz as seguintes propriedades:
ˆ
dM (X;Y ) = 0 sse X = Y
ˆ
dM (X;Y ) = dM (Y;X) 8 X;Y 2 I
ˆ
dM (X;Y ) dM (X;Z)+dM (Z;Y ) 8 Z;X;Y 2 I
Demonstração.
!
Veja em (MOORE, 1979)
Contudo, uma vez que
I é não vazio e a função dM
está denida sobre
I , então o
(I ;dM ) é um espaço métrico.
Uma vez que A 6= B , então a < b ou a < b. Dessa maneira, sem perda de generalidade,
vamos supor que a < b (no outro caso é dual).
Dado o espaço métrico (I ;dM ) e um subconjunto H I , denimos o diametro de
H, denotado por diam(H), como
par
diam(H) = fdM (X;Y ) j X;Y 2 Hg;
G
onde
F
denota o supremo com respeito à ordem usual da reta e
Moore. Devemos observar que
(3.3)
dM
é a distância de
diam(H) pode ser innito em alguns casos.
Denição 3.18. Um subconjunto
diam(X) 2 R+ .
X
de um espaço métrico (I ;dM ) é limitado se
I de I(R) é limitado com respeito à métrica
de Moore se estiver contido em I[A;B ] para algum A;B 2 I(R)
Claramente temos que um subconjunto
3.4 Topologia no
27
I(R)
Lema 3.1 (Lema da Completude). Seja H um subconjunto limitado de I(R). Denimos H = fc j C 2 Hg e H = fc j C 2 Hg. Então, o supremo e o ínmo de H
d
F
com respeito à ordem de Kulisch-Miranker, representado por H e H, são os
d d
F
F
intervalos [ H; H] e [ H; H], respectivamente.
Demonstração.
ver (BEDREGAL; BEDREGAL, 2010)
Lema 3.2. Sejam
I e J subconjuntos limitados de I(R) e
I + J = f X +Y j X 2 I ; Y 2 J g:
Então,
l
Demonstração.
(I + J ) = I + J
l
l
e
(I + J ) = I + J
G
G
G
veja (BEDREGAL; BEDREGAL, 2010)
Denição 3.19. Seja
dado por:
X 2 I( R).
O módulo de
X
é um número real não negativo
jX j = maxfjxj; jxjg 0
(3.4)
Geometricamente, o módulo do intervalo corresponde à maior distância do centro
da reta dos reais ( ponto 0) até um dos extremos.
Teorema 3.1. Sejam
X;Y 2 I(R). As seguintes propriedades se vericam:
1. jX j = 0 , X = [0;0]
2. jX +Y j jX j + jY j
3. jX Y j = jX jjY j
Demonstração.
Veja em (SANTOS, 2001)
Denição 3.20 (Denição de Função Intervalar). Uma função F é chamada de função intervalar se o seu domínio e o contradomínio são subconjuntos de I(R).
Denição 3.21. Seja F : I ! I(R) uma função intervalar ela é considerada uma
inclusão monotônica se para todo A;B 2 I tal que A B temos que F(A) F(B).
3.5 Integração Intervalar
28
Denição 3.22. Uma função intervalar F é dita limitada se, a imagem de F for
limitada, ou seja, está contida em I[A;B] para algum A;B 2 I(R). Neste caso,
A k F(X) k B , para todo X pertencente ao domínio de F .
F : I ! I(R), denimos as funções F : I ! R e
F : I ! R por F(X) = F(X) e F(X) = F(X), respectivamente.
Corolário 3.1. Seja I I(R) e F : I ! I(R) uma função intervalar limitada. Então
o subconjunto F(I ) = fF(X) 2 I(R) j X 2 Ig tem supremo e inmo com respeito à
Como notação, sendo a função
ordem de Kulisch-Miranker. De fato:
G
l
Demonstração.
3.5
3.5.1
F(I ) = [ F(I ); F(I )]
G
G
F(I ) = [ F(I ); F(I )]
l
l
veja em (BEDREGAL; BEDREGAL, 2010)
Integração Intervalar
Integral de Moore e Yang
Denição 3.23. Seja A um intervalo e F função intervalar contínua3 e uma inclusão monotônica com respeito a dM . A Soma de Riemann da função F para
uma partição P de A é denida como:
nX1
X
(F; P ) = F([xk ;xk 1])d(xk ;xk 1)
k=0
Onde d é a métrica usual sobre números reais d(x;y) = jy
e Yang no intervalo A é denida como:
Z
F(X)dX =
A
\
xj. A integral de Moore
(F; P )
X
P2P(A)
Teorema 3.2 (Teorema de Caracterização). Seja A um intervalo,
intervalar contínua e inclusão monotônica. Então
Z
A
3 Veja
F(X)dX =
"
Z
a
a
Z
a
#
fl(x)dx; a fr (x)dx
a denição em (MOORE; STROTHER; YANG, 1960)
F
uma função
3.5 Integração Intervalar
29
onde fl (x) = 1 (F[x;x]) e fr (x) = 2 (F[x;x])
Demonstração.
3.5.2
Veja em (MOORE; STROTHER; YANG, 1960)
Integral de Bedregal-Bedregal
Denição 3.24. Seja F : I[A;B] ! I(R) uma função intervalar contínua. Dada uma
partição P de I[A;B] . Nós denimos os seguintes Somatórios de Riemann de F
com respeito a P
ˆ Soma de Riemann Inferior
(F; P ) =
n
X
k
=1
l
F(I[X
k
1 ;Xk
] )dM (Xk 1 ;Xk )
ˆ Soma de Riemann Superior
X
Onde F(I[X
k
1 ;Xk
(F; P ) =
n G
X
k
=1
] ) = fF(X) j X 2 I[X
F(I[X
1 ;Xk
k
k
1 ;Xk
] )dM (Xk 1 ;Xk )
]g
Denição 3.25. Seja F : I[A;B] ! I(R) uma função intervalar contínua. Nós deniR
mos como a integral inferior da função F de A até B , denotada como AB F(X)dX ,
por
Z
B
F(X)dX =
A
G
P2P[A;B ]
e a denição da integral superior da função
RB
A F(X)dX , como sendo:
Z
B
F(X)dX =
A
(F; P )
F
X
l
P2P[A;B ]
de
A
B
A
Demonstração.
F(X)dX =
"
Z
B,
! I(R) uma função in-
dM (A;B)
F
F
r (x)dx
l (x)dx;
b a
a
a
b
Z
b
denotada como
(F; P )
Teorema 3.3 (Teorema de Caracterização). Seja F : I[A;B]
tervalar contínua, então F é uma função integrável e
Z
até
#
Veja em (BEDREGAL; BEDREGAL, 2010)
30
4 Integral de Linha Intervalar
Nessa seção apresentaremos a noção de integral de linha intervalar, bem como as
denições, teoremas, corolários, proposições e lemas necessários para a fundamentação.
Denição 4.1. Um caminho em I(R) é uma aplicação : I
é um intervalo I = [c;d] R.
! I(R), cujo domínio
: I ! I(R), denimos as funções : I ! R e
: I ! R por (x) = (x) e (x) = (x), respectivamente. Assim para cada t 2 I
temos que (t) = [(t);(t)].
Denição 4.2. O caminho é contínuo (resp. diferenciável) no ponto a 2 I se
cada uma das funções (t) e (t) forem contínuas (resp. diferenciáveis) em a:
Se for diferenciável em a dene-se a derivada do caminho no ponto a por
0(a) = (0(a);0(a)) 2 R2: A norma k 0(a) k= Maxfj 0(a) j; j 0(a) jg chama-se valor
absoluto da variação de em a:
Denição 4.3. Seja F : I[A;B] ! I(R) uma função intervalar limitada e : [c;d] !
I[A;B] um caminho de classe C 1. Dada a partição P de [c;d], denimos as seguintes
Somas de Riemann de F com respeito de e P :
Como notação, sendo a função
Somatório inferior de Riemann
(F;; P ) =
n
X
k
=1
l
F(I[(x
1
k
);(x )] )dM ((xk 1 );(xk ))
k
Somatório superior de Riemann
(F;; P ) =
X
Quando F(I[(x );(x )] )
k
1
k
n G
X
k
=1
F(I[(x
k
1
);(x )] )dM ((xk 1 );(xk ))
= fF((t))jt 2 [c;d]g
k
4 Integral de Linha Intervalar
31
F : I[A;B] ! I(R) uma função limitada e P
: [c;d] ! I[A;B] um caminho de classe C 1, então.
Lema 4.1. Seja
uma partição de
I
e
(F;; P ) (F;; P )
X
Demonstração. Para todo k = 0;1;2;:::;n 1, F(I[(x
e dM (((xi 1 );(y)) > 0. Então podemos escrever.
l
l
F(I[(x
);(x )] )
(F;; P ) (i 1)
G
(i 1)
F(I[(x
(F;; P )
(i 1)
i
);(x )] ) i
G
F(I[(x
(i 1)
);(x )] )
i
);(x )] )
i
X
Proposição 4.1. Seja : [c;d] ! I[A;B] um caminho de classe C 1 , F : I[A;B] ! I(R)
uma função limitada e sejam P 0 e P partições do intervalo I = [c;d]. Se P 0 4 P
então
X
(F;; P ) (F;; P 0) X(F;; P 0) (F;; P ):
Demonstração. Tomemos uma partição P onde P = fc = x0 ;:::;xn = dg e P 0 de maneira
0
que P = fa = x0 ;:::y:::;xn = bg Sabendo que a distância é:
dM ((xi 1);(y))+dM ((y);(xi)) = dM ((xi 1);(xi))
Também temos que:
l
F(I[(x
e também
l
)
1) );(x )]
(i
i
F(I[(x
(i 1)
l
F(I[(x
(i 1)
);(y)) )
);(x ) ) F(I[(y);(x )) )
i
l
i
4 Integral de Linha Intervalar
32
Por outro lado:
(F;; P 0)
=
1
iX l
k
=1l
F(I[(x
k
1
);(x )] )dM ((xk 1 );(xk ))
k
+ F(I[(x );(y)])dM ((xi 1);(y))
l
+ F(I[(y);(x )])dM ((y);(xi))
+
1l
nX
=
k i
1
iX l
k
=1l
1
i
i
F(I[(x );(x
k+1
k
F(I[(x
k
1
)] )dM ((xk );(xk+1 ))
);(x )] )dM ((xk 1 );(xk ))
k
+ F(I[(x );(x )])dM ((xi 1);(y))
l
+ F(I[(y);(x )])dM ((y);(xi))
+
=
1l
nX
=
k i
1
iX l
k
=1l
1
i
i
i
F(I[(x );(x
k+1
k
F(I[(x
k
+ F(I[(x
i
1l
1
1
)] )dM ((xk );(xk+1 ))
);(x )] )dM ((xk 1 );(xk ))
k
);(x )] (dM ((xi 1 );(y))+dM ((y);(xi )))
i
nX
+
F(I[(x );(x
k=i
= (F;; P )
k
k+1
)] )dM ((xk );(xk+1 ))
Provaremos agora que
(F;; P 0) (F;; P 0)
Temos que para todo k = 0;:::;n
1 d F(I[(x );(x )]) F(I[(x );(x
X
F
k+1
k
l
F(I[(x );(x
k
k+1
)] )dM ((xk+1 );(xk ))
(F;; P 0) G
k+1
k
F(I[(x );(x
(F;; P 0)
k
k+1
)] ) logo
)] )dM ((xk+1 );(xk ))
X
Como parte nal da demonstração do teorema provaremos que
X
(F;; P 0) (F;; P )
X
Também temos que:
G
F(I[(x
(i
)
1) );(x )]
i
G
F(I[(x
(i
)e
1) );(y ))
G
F(I[(x
(i
)
1) );(x )
i
G
F(I[(y);(x )))
i
4 Integral de Linha Intervalar
33
Por outro lado:
(F;; P 0)
X
=
1
iX G
F(I[(x );(x )])dM ((xk 1);(xk ))
+ F(I[(x );(y)])dM ((xi 1);(y))
+ F(I[(y);(x )])dM ((y);(xi))
n 1
+
F(I[(x );(x )])dM ((xk );(xk+1))
k
=1G
k
i
1
k
1
G
i
X G
=
1
k+1
k
k i
iX G
F(I[(x );(x )])dM ((xk 1);(xk ))
+ F(I[(x );(x )])dM ((xi 1);(y))
+ F(I[(y);(x )])dM ((y);(xi))
n 1
+
F(I[(x );(x )])dM ((xk );(xk+1))
k
=1G
k
i
1
1
k
i
G
i
X G
=
=
1
k+1
k
k i
iX G
F(I[(x );(x )])dM ((xk 1);(xk ))
+ F(I[(x );(x )])[dM ((xi 1);(y))+dM ((y);(xi))]
n 1
F(I[(x );(x )])dM ((xk );(xk+1)) = (F;; P )
+
k
=1G
k
i
1
1
k
i
X
X G
=
k
k i
Corolário 4.1. Seja F : I[A;B] ! I(R) e
Q partições de I , se P 4 Q temos:
k+1
: [c;d] ! I[A;B] funções limitadas e P e
(F;; P ) (F;; Q)
X
Demonstração.
(F;; P ) (F;; P [Q) (F;; P [Q) (F;; Q)
X
X
Denição 4.4. Seja F : [a;b] ! I(R) uma função limitada. Deniremos a integral
inferior e a integral superior como sendo, respectivamente:
Z
F(X)dS =
G
()
P 2P I
(F;; P )
4 Integral de Linha Intervalar
Z
34
F(X)dS =
Proposição 4.2. Seja F : I[A;B]
de tal que C F((x)) D 8
nós temos que
(F;; P )
X
l
()
P 2P I
! I(R) e : [c;d] ! I[A;B] seja uma função limitada
X 2 I[A;B]. Então para cada partição P de I = [c;d]
Z
Z
CdM ((c);(d)) (F;; P ) F(X)dS F(X)dS (F;; P ) DdM ((c);(d))
X
P> = [c;d] uma partição trivial de I .
(F;; P>) (F;; P ). Mas por denição temos que
Demonstração.
Seja
Pelo Lema 3.1 temos que
(F;; P>) = F(I[(c);(d)])dM ((c);(d)) CdM ((c);(d))
l
Tomando o resultado do Corolário 4.1, podemos concluir que
R
F(X)dS F(X)dS .
R
Para a terceira parte da desigualdade, tomemos por denição,
(F;; P>) = F(I[(c);(d)])dM ((c);(d)) DdM ((c);(d))
X
G
Proposição 4.3. Seja P0 e P00 subconjuntos de P[I] satisfazendo a seguinte propriedade:
X
8 P 2 P[I]9P 0 2 P0 e P 00 2 P00 tal que (F;; P ) (F;; P 0) e (F;; P 00) X
(F;; P ) Então
e
Z
F(X)dS =
Z
F(X)dS =
G
P 0 2P0
l
(F;; P 0)
X
P 00 2P00
(F;; P 00)
Corolário 4.2. Seja c y b um número real que y 2 [c;d], e P0 [I] um subconjunto
de P[I] que contém c. Então:
Z
F(X)dS =
Z
Demonstração.
F(X)dS =
Seja a partição
G
(F;; P )
P2P0
l X
P2P0
(F;; P )
P 2 P[I], P 0 = P [ fcg.
Sendo
P0
é mais na que
4 Integral de Linha Intervalar
P,
temos que
35
(F;; P ) (F;; P 0) e (F;; P 0) (F;; P ).
P
P
Deste modo,
P0
[I],
satisfazendo a condição da proposição acima.
Proposição 4.4. Seja
Z
b
c
Z
b
c
c < y < b seja um número real tal que y 2 [c;b]. Então:
F((t))k0(t)kdt
F((t))k0(t)kdt
Demonstração.
Seja
IeJ
=
Z
=
Z
y
c
y
c
F((t))k0(t)kdt+
Z
F((t))k0(t)kdt+
Z
b
y
F((t))k0(t)kdt
b
0 (t)kdt
F((t))
k
y
conjuntos de Somatório inferior de Riemann de
F j[c;y] e
F j[y;b], respectivamente. Então, podemos dizer que I + J é o conjunto somatório inferior
de Riemann da função F . Tendo os resultados do 3.2 e 4.2, temos que:
Z
b
F((t))k0(t)kdt =
c
=
=
(I + J )
(I )+ (J )
y
0 (t)kdt+ b F((t))k0 (t)kdt
F((t))
k
c
y
G
G
Z
G
Z
De maneira análoga temos obtemos o resultado para o somatório superior de Riemman.
Denição 4.5. Uma função limitada F : I[A;B] ! I(R) dizemos que é uma função
integrável com respeito ao caminho : [c;d] ! I[A;B] se
Z
Z
F(X)dS = F(X)dS
Este valor comum é chamado
de integral intervalar curvilínea de
Z
de e é denotada por F(X)dS
F
com respeito
Denição 4.6. Seja F : I[A;B] ! I(R) uma função denida limitada. Dena o
menor e o maior espectro de F , chamamos de Fl e Fr , respectivamente:
F(x) = 1F[x;x] e F(x) = 2F[x;x]
Teorema 4.1. Seja : [c;d] ! I[A;B] um caminho de classe C 1 e
uma função limitada. Então
Z
F(X)dS =
"
Z
d
c
F((x)) k 0(x) k dx;
Z
d
c
F : I[A;B] ! IR
F((x)) k 0(x) k dx
#
4 Integral de Linha Intervalar
e
Z
F(X)dS =
"
Z
d
c
36
F((x)) k 0(x) k dx;
Z
d
c
F((x)) k 0(x) k dx
#
Demonstração. Tomemos o conjunto de partições da imagem de : [c;d] ! I[A;B] ,
Pn = fA = X0;X1;:::;Xn = B g, onde A = (c) e B = (d) onde vinda da partição do
domínio de da forma T = fc = t0 ;t1 ;:::;tn = dg quando
dM ((tk );(tk+1)) = k0(tk )ktk
. Contudo
Z
F(X)dS =
=
=
=
G
n2N
(F;; P )
1l
G n
X
=0
1l
n2N k
G n
X
=0
n2N k
nX l
1
2
4
=0
1l
k
nX
k
=0
F(I[(x );(x
)] )dM ((xk );(xk+1 ))
F(I[(x );(x
)] )k0 (xk )kxk
k+1
k
k+1
k
F(I[(x );(x
k
k+1
3
F(I[(x );(x
k+1
k
)] )k0 (xk )kxk ;
)]
)k0(xk )kxk 5
Por outro lado:
Z
1
G n
X
d
F((x))k0(x)kdx =
c
=
=0
1
n 2N k
G n
X
n 2N k
=0
F((xk ))d((xk );(xk+1))
F((xk ))k0(xk )kxk
De maneira análoga temos:
Z
d
F((x))k0(x)kdx =
c
1
G n
X
n2N k
=0
F((xk ))k0(xk )kxk
Ou seja, podemos ter identidade:
1l
G n
X
n2N k
=0
F(I[(x );(x
k
k+1
)]
)k0(xk )kxk =
1
G n
X
n 2N k
=0
F((xk ))k0(xk )kxk
4 Integral de Linha Intervalar
1l
G n
X
n2N k
=0
37
F(I[(x );(x
k+1
k
1
G n
X
)] )k0 (xk )kxk =
n 2N k
F((xk ))k0(xk )kxk
=0
Claramente, temos que:
l
F(I[(x );(x
k+1
k
)] )
F((xk ))
Deste modo:
1l
G n
X
n2N k
=0
F(I[(x );(x
k
k+1
)]
)k0(xk )kxk
1
G n
X
n 2N k
=0
F((xk ))k0(xk )kxk
I[(x );(x )] é compacto e F é uma função contínua, nós
d
temos que 9 yk 2 [xk ;xk+1 ] tal que
F(I[(x );(x )]) = F((yk )) e , pelo mesmo fato,
Inversamente, uma vez que
k+1
k
k+1
" > 0,
9 > 0 tal que dM (X;Y ) então d(F(X);F(Y )) " Considerando dM ((c);(d)) 0
A partir de yk 2 [xk ;xk+1 ] nós temos que:
a função
F
k
é uniformemente contínua. Com isso podemos dizer que, dado um
dM ((xk );(yk )) dM ((xk );(xk+1)) = k0(xk )ktk Sendo
F uniformemente contínua nós temos que d(F((xk );F((yk ))) ". Contudo:
1
X
G n
n2N k
=0
F((xk ))k0(xk )kxk
G
1
nX =0
1
n2N k
G n
X
n2N k
=0
F((xk ))
F((xk ))
1l
X
G n
n 2N k
l
=0
F(I[(x );(x
F(I[(x );(x
F((yk ))
k+1
k
k
k+1
)]
)] )k0 (xk )kxk =
k0(xk )kxk =
k0(xk )kxk 1
G n
X
n 2N k
=0
"k0(xk )kxk = "
Com isso provamos que:
1l
G n
X
n2N k
=0
F(I[(x );(x
k
k+1
)] )k0 (xk )kxk =
1
G n
X
n 2N k
=0
F((xk ))k0(xk )kxk
Teorema 4.2 (Teorema de Caracterização). Seja : [c;d] ! I[A;B] um caminho de
classe C 1 e F : I[A;B] ! IR uma função contínua. Então, F é uma função inte-
4 Integral de Linha Intervalar
38
grável com respeito de e
Z
F(X)dS =
Demonstração.
Sendo
"
Z
d
c
F((x)) k 0(x) k dx;
Z
d
c
F((x)) k 0(x) k dx
#
(4.1)
F uma função contínua, nós temos que F e F , também funções
contínuas. Contudo pela denição 4.5 e pelo teorema 4.1 podemos dizer que:
Z
Z
d
F((x)) k 0(x) k dx =
c
d
0 (x) k dx =
F((x))
k
c
Z
d
c
Z
F((x)) k 0(x) k dx
d
0 (x) k dx
F((x))
k
c
Contudo, podemos escrever a integração como sendo:
Z
F(X)dS =
"
Z
c
d
F((x)) k 0(x) k dx;
Z
d
c
#
F((x)) k 0(x) k dx
:
39
5 Aplicação da Integral Intervalar
de Linha Intervalar
As teorias que forma a Física Clássica são um excelente suporte para a análise dos
fenômenos ligados a partículas macroscópicas, bem como os eventos ligados a ela. Contudo ao serem aplicadas na análise de partículas microscópicas não se tem a eciência
desejada. Classicamente existem dois conceitos distintos sobre onda e partícula. Contudo no nal do século XIX e no início do século XX foram coletadas muitas informações
a respeito dos fenomênos microscópios que zeram esquecer as teorias da física clássica
e pensar nas características das partículas microscópicas e os fenomênos relacionados
a elas.
Essas mudanças foram possíveis graças a alguns experimentos, descritos em
(BEECHING, 2007), em que destacamos:
Radiação de corpo negro
:
Para explicar a radiação eletromagnética emitida por
um corpo em equilíbrio térmico, Planck postulou que a energia eletromagnética
não varia continuamente, mas sim é um pacote é um múltiplo de um quantidade
mínima de energia.
Efeito fotoelétrico
: Explicado por Eistein, o efeito fotoelétrico foi proposto por Hertz
em 1897. Para solucionar a falta de um argumentação mais forte, Eistein propos
que a luz é um composto de várias partículas chamadas
uma energia equivalente a
ergs.s e
v
hv, onde h
quantas,
é a constante de Planck,
que possuem
h = 6:626 10
27
é a frequência da luz.
Efeito Compton
: Em 1924 Compton descobriu que a radiação eletromagnética não
era espalhada de modo consistente com a natureza ondulatória dado que em colisões a radiação comporta-se como um feixe de partículas as quais possuem energia
hv
e o momento
hv onde
c
c é a velocidade da luz.
5.1 Difração de uma Partícula
Difração de Elétrons por David e Germer
40
: Publicado em (DARROW, 1948) os
estudos de David e Germer sobre a difração de elétrons mostraram que a matéria
e a radiação possuem características equiparáveis Os resultados dos experimentos
citados levam a crer que a radiação eletromagnética pode-se comportar como uma
partícula em determinadas situações, causando o que é dito como um comportamento de dualidade. A propagação do elétron é ondulatória e quando existem
colisões o comportamento passa a ser algo corpuscular.
5.1
Difração de uma Partícula
Na década de 1920 surgiu na física uma teoria que viria a ser o principal foco,
segundo (D'ESPAGNAT, 1979) para a análise das estruturas e comportamento da matéria: a mecânica quântica.
O estudo desse campo da física oferece recursos teóricos
para descrever o comportamento das moléculas, átomos e partículas sub-atômicas.
Segundo (SQUIRES, 1993) desde a sua criação a mecânica quântica apresentou problemas de interpretação em grau sem precedentes na história da ciência. As diculdades
interpretativas dessa teoria dizem respeito tanto à forma pela qual a teoria se relaciona
com os fenômenos quanto ao delineamento de uma ontologia que lhe seja apropriada.
A compreensão desse ponto requer uma breve menção às duas noções fundamentais das
teorias físicas: a de estado e a de grandeza física. De um modo geral, estados são caracterizações básicas dos objetos físicos tratados pela teoria. As grandezas físicas são as
propriedades mensuráveis desses objetos. Para efeitos de comparação, podemos lembrar
que na mecânica clássica o estado de uma partícula de massa
m
é representado por um
conjunto de seis números que especicam sua posição e velocidade. Em função desses
números a teoria indica como calcular os valores de grandezas físicas.
Na mecânica quântica os estados dos objetos são denidos por meio das chamadas
funções de onda.
É justamente dessa nova (e complexa) forma de representação dos
estados que surgem quase todos os problemas de interpretação da teoria.
Uma grandeza física só será relevante do ponto de vista prático se pudermos atribuir
valores a ela. Contudo essa é a primeira e mais fundamental diculdade interpretativa
na mecânica quântica:
Dado um estado quântico e uma grandeza física, em geral o
5.2 Experimento
41
formalismo quântico simplesmente não atribui um valor à grandeza e mesmo quando
o estado não fornece o valor de uma grandeza física, medidas dessa grandeza sobre o
objeto são inteiramente possíveis e dão valores bem denidos. Em (SINGH, 2004) essa
diculdade de predição dos fenômenos, dos resultados de medida, fez com que surgissem
maneiras diferentes de interpretar:
Incompletude:
A descrição quântica do objeto é
incompleta, ou seja, não prevê valores
de grandezas perfeitamente mensuráveis.
Completude:
Os valores dessas grandezas não existem, ou não estão denidos antes
que se efetue a medida; a medida então criaria ou tornaria denidos os valores,
não sendo propriamente uma medida algo puramente incerto no sentido usual
do termo, ou seja, a mera revelação de uma propriedade preexistente do objeto
investigado.
Apesar das duas correntes não trabalharem juntas, nenhuma delas elimina a incerteza. Isso nos possibilita dizer que a mecânica quântica não está isenta da diculdades
teóricas, conceituais e losócas.
5.2
Experimento
Mauricee de Broglie, físico experimental francês que, desde o princípio, apoiou a
teoria sobre o
efeito Compton 1 em relação à natureza corpuscular da radiação.
Segundo
(EISBERG; RESNICK, 1985) dentre os seus trabalhos, um dos principais é chamado de
Postulado de Broglie, onde armara que o comportamento dual, isto é, onda-partícula,
da radiação também se aplicava à matéria. Assim como um fóton tem associada a ele
uma onda luminosa que governa seu movimento, também uma partícula material tem
associada a ele uma onda de matéria que governa seu movimento.
O experimento, ilustrado na gura 5.1, consiste na emissão de elétrons em uma
fenda estreita de largura
y.
O deslocamento dos elétrons ocorre devido a submissão
das partículas a uma diferença de potêncial gerada por uma força eletroestática, de
1 consiste
na alteração do comprimento de onda de um fóton ao iteragir com a matéria. Essa alteração
se dá pelo ganho ou perda de energia.
5.2 Experimento
42
maneira tal que os elétrons se deslocam paralelos ao eixo
partícula sofre uma difração, ou seja, o ângulo
variação do valor da coordenada
por
x.
Ao passar pela fenda a
representa a amplitude angular da
y da partícula em determinado momento e é calculado
sen() = y , onde é o comprimento de onda do elétron. Como a propragação da
onda governa o movimento da partícula, também da as probabilidades relativas que o
elétron tem de alcançar diferentes pontos na chapa fotográca que ca à frente da fenda
para receber o elétron. Portanto, o elétron que passa pela fenda será deetido para um
ângulo qualquer entre
e +. Embora seu momento na direção y fosse conhecido com
grande precisão antes de passar pela fenda, após passar pela fenda, seu momento na
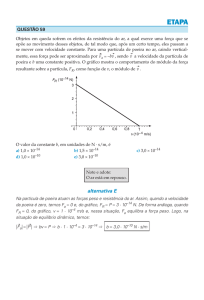
y pode ter qualquer valor entre py e +py , com o valor do ângulo sen() = pp .
Sendo assim, o momento na direção y do elétron torna-se impreciso devido a difração
y
direção
da onda do elétron. É possível ter uma valoração da incerteza pela equação abaixo:
p
py ' py = p sen() = y
(5.1)
Figura 5.1: Representação do experimento de difração de uma partícula por uma fenda
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
5.3
43
Modelagem Intervalar do Experimento de Difração
de uma Partícula
Os modelos de experimentos de difração de elétrons utilizados, não consideram
alguma das variáveis mais importantes quando se trata de um elétron que é a sua
carga. Sabemos que devido à própria natureza da partícula, ela não vê o ambiente
como um corpo sólido ou como um campo de energia, mas sim como um ambiente
reticulado formado por partículas subatômicas.
O elétron ao passar pela fenda sofre
uma alteração em seu movimento devido a que existem na fenda alguns milhares de
elétrons que juntos formam uma diferença de potencial que interfere diretamente em
seu movimento. Mauricee de Broglie, como descrito em (EISBERG; RESNICK, 1985),
também considerou a diferença de potêncial elétrico em seu experimento, mas somente
para fazer o movimento da carga, e não em todo o experimento. O que faremos então
é calcular o trabalho realizado por essa partícula ao longo de sua trajetória dentro
da fenda utilizando a noção de intervalo para representar a incerteza sobre a posição
relativa(representado na gura 5.2 por pequenas circunferências verdes) da partícula
em um determinado instante. Essa incerteza da sua posição implica em uma incerteza
quanto à diferença de potencial, pois a denição de potencial está ligada a posição
relativa das partículas envolvidas.
Figura 5.2: Representação da fenda sob uma visão subatômica
Na gura 5.2 força eletroestática implementada
F
obriga a partícula a entrar na
fenda, contudo o movimento não é linear devido a existência dos elétrons (representa-
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
44
dos na gura pela círculo de cor cinza) dos átomos das paredes que, juntos, aplicam
à partícula uma força.
Segundo (HALLIDAY; RESNICK, 2007), o valor escalar da
força eletroestática, de atração ou repulsão entre duas cargas puntiformes cujos valores
escalares são
Onde
k
é a
q1 e q2 e que estão separadas pela distância D, é dado por:
F = k qD1q22
constante eletrostática
que tem o seguinte valor:
1 = 8;99 109 N:m2
k = 4"
C2
0
C é a é a quantidade de carga elétrica carregada pela corrente de 1 ampère
durante 1 segundo e N A constante "0 (constante de permissividade ) possui o valor:
2
C
12
"0 = 8;85 10 N:m2
Onde
Lembrando de que existe uma força de repulsão sob a partícula devido aos seus
elétrons. Com isso, pensando em uma quantidade discreta e enumerável de elétrons das
paredes da fenda, podemos somar todas as forças que atuam sobre a partícula lançada na
fenda de acordo com a proporção da distância de cada átomo da fenda com a partícula
lançada em cada momento.
Como a matéria é constituida de um único material, a
distância entre os átomos é constante, a qual será representada por
l na gura 5.3.
Figura 5.3: Representação geométrica das distâncias dos átomos das paredes e do
elétron lançado á fenda
No instante em que o elétron lançado entra na fenda, ele recebe somente uma força
favorável ao seu movimento ( que é a força inicial), as outras forças geradas pelos elétrons
dos átomos das pareces são forças de sentido oposto ao sentido da força inicial, então
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
45
podemos considerar a seguinte força contrária:
F =
Onde
X
1
kq2 (x2 +(nl)
2)
i=1
n
(5.2)
i é o valor índice da partícula atual, e n é o número de átomos que se encontram
na parede da fenda. A força de sentido oposto ao da força inicial é derivada da força
F , representada na equação 5.2.
Sendo a força inicial é paralela ao eixo
sentido oposto ao da força inicial é o cosseno da força
F , 5.2. Logo:
n
1 cos(i)
Fcos = kq2 (x2 +(il)
2)
i=1
n
1 il
2
Fcos = kq (x2 +(il)
2 ) x2 +(il)2
i=1
n
il
Fcos = kq2
2
2
i=1 (x +(il) )
x, a força de
X
X
q
X
(5.3)
3
2
Naturalmente que a medida que o elétron avança em sua trajetória, o número de
elétrons a sua frente diminui e consequentemente a força de resistência diminui e a força
de repulsão aumenta, podemos caracterizar isso como:
(t) = Fcos(t) Fcos(n t)
t
n t
il
il
2
(t) = kq2
kq
2
2
2
2
i=1 (x +(il) )
i=1 (x +(il) )
X
X
3
2
Onde
t é o índice corrente do movimento.
3
2
Até agora tomamos o valor
(5.4)
x como um
valor exato, contudo sabemos que a posição relativa do elétron está entre duas posições
extremas - representadas na gura 5.2 pelas pequenas circunferências cinzas. As posições
são mapeadas por uma função intervalar:
: [c;d] ! I[A;B]
(t) = [(t);(t)]
(5.5)
Pela característica da hipótese de movimento tomemos uma função
(t) que descreve o
movimento em seu gráco. A função intervalar sendo:
4t ; 4t +2
(t) = 2 4t+N
+1 4t+N +1
(5.6)
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
46
Onde o gráco dos seus extremos é representado pelo gráco na gura abaixo
Onde os extremos do intervalo representam as posições extremos em cada instante.
, na equação 5.4 como:
n t
i
2
2 (5.7)
i=1 (dM ((t);Y (t)) +(il) )
Tomando a distância de Moore, podemos redenir a função
i
(t) = kq2l
2
2
i=1 (dM ((t);Y (t)) +(il) )
2
4
3
t
X
X
3
2
3
2
5
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
47
Figura 5.4: Gráco da força gerada pelo campo elétrico gerado pelos elétrons da fenda
A equação 5.7 é a equação que representa a força de interferência gerada pelo campo
de elétrons no movimento da partícula sobre a partícula lançada na fenda, contudo
devemos lembrar que existe uma força aplicada a partícula que a faz propagar. Essa
força
Fini é denida intervalar como:
F : I[A;B] IR ! IR
F(A) = [F(A);F(A)]
(5.8)
A força inicial gerada para forçar o deslocamento da partícula é dada por:
Onde
P
q1 q2
Fini((t)) = k d ((t);P)
2
M
representa a posição da fonte da força de deslocamento da partícula.
Con-
tudo, devemos lembrar que no processo de deslocamento da partícula, a força que atua
no movimento, sofre uma variação devido as outras forças que atuam no sistema - representada pela equação 5.7. Pelo fato do movimento da partícula ser intervalar, não
sabemos ao certo se dado um instânte
t a partícula está sob a ação de uma força gerada
pelo campo elétrico da parede ou não. Então vamos tomar duas posibilidades para o
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
48
movimento:
Movimento 1
Caso a partícula só seja submetida ao campo elétrico gerado pelas pa-
redes após passar pela metade do trajeto.
Movimento 2
Caso a partícula só seja submetida ao campo elétrico gerado pelas pa-
redes antes de passar pela metade do trajeto, na outra metade ela seja livre do
campo.
Como é possível ver na gura 5.3 antes da partícula chegar a metade do seu trajeto
o sentido da força do campo é oposto ao sentido do movimento, o que faz com que o
movimento seja, em parte, retardado. Após a metade do trajeto o sentido da força do
campo das paredes da fenda é favorável ao movimento, o que seria uma força adicional a
Movimento 1 a força que atua sobre a partícula é
maior favorencendo o deslocamento da partícula, enquanto no Movimento 2 a partícula
expulsão da partícula. Ou seja, no
se desloca com uma força menor favorecendo o seu deslocamento no sentido de expulsão
da fenda. Esses dois casos devem ser levados em consideração, ao mesmo tempo, tendo
em vista que, não se sabe a posição exata da partícula dado um instânte
podemos denir a função 5.8 como sendo:
8
>
<
N
F
ini ((t))+(t); se t < 2
F((t)) =
Fini((t)); se t N2
>
:
8
>
<
N
F
ini ((t)); se t < 2
F((t)) =
Fini((t))+(t); se t N2
>
:
t.
Portanto
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
49
Figura 5.5: Gráco da função intervalar resultante
O trabalho realizado pela partícula
Segundo (GUIDORIZZI, 1989, pág.1097-1099) dado um campo vetorial contínuo
!
F : Rn ! Rn (onde é um aberto no Rn) que representa a força aplicada a uma
: [a;b] ! , contínua e derivável. O trabalho W realizado pela partícula durante a trajetória pode ser calculada pela integral
partícula de trajetória denida pela curva
curvilínea
b
W = !
F d = a !
F ((t)) 0(t)dt
Z
Z
No experimento tratado, a função que representa a força, tem somente variação puramente escalar, com isso podemos considerar a
integral de linha,
curvilínea, para o cálculo do trabalho da partícula.
ao invés da
integral
Sendo o modelo intervalar, se faz
necessário um modelo de integração que seja fundamentada sobre um espaço intervalar,
com isso utilizaremos o modelo proposto em (BEDREGAL; BEDREGAL, 2010). Assim
precisamos Tomando a equação 5.6 que representa a função caminho e pela denição
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
50
4.2, podemos exprimir uma função paramétrica da forma:
0 : I !
t 7!
R
2
404 ; 404
(4t+101)2 (4t+101)2
!
Com isso o trabalho calculado, segundo a integral de linha intervalar, pode ser montada
como:
Z
F(X)dS =
"
Z
c
d
Z
#
d
F((t)) k 0(t) k dt; c F((t)) k 0(t) k dt :
(5.9)
Sabendo que
k 0(t) k = Maxfj 0(t)j; j 0(t)jg
(
404 ; 404
(4t+101)2 (4t+101)2
= Max
404
= (4t+101)
2
)
Logo a equação 5.9 ca como:
Z
404 dt; dF((t)) 404 dt :
F((t))
F(X)dS
=
(4t+101)2 c
(4t+101)2
c
No caso de
Z
"
Rd
c
#
(5.10)
404 dt
F((t)) (4t+101)
2
404 dt =
F((t))
(4t+101)2
c
Rd
c
8 Z
>
>
>
<
404 dt; se t < N
(F
ini ((t))+(t))
(4t+101)2
2
c
d
404
N
Fini((t)) (4t+101)2 dt; se t 2
c
d
Z
>
>
>
:
(5.11)
404 dt
F((t)) (4t+101)
404 dt =
F((t))
(4t+101)2
c
d
Z
d
d
E no caso de
Z
Z
2
8
>
>
>
<
>
>
>
:
404 dt; se t < N
F
ini ((t))
(4t+101)2
2
c
d
404
N
(Fini((t))+(t)) (4t+101)2 dt; se t 2
c
Z
Z
d
(5.12)
Contudo para termos valores reais utilizamos um método numérico para a integração,
isso devido a função ter características que impedem uma integração direta.
Para executar a operação de integração clássica e gerar os grácos utilizamos o
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
51
Maple versão 12. As equações 5.11 e 5.12 são denidas por duas funções
Rd
404
404
c Fini ((t)) (4t+101) dt e c (Fini ((t))+(t)) (4t+101) dt que, utilizando o método dos
software
Rd
2
2
mínimos quadrados e em seguida o método de uma integral numérica baseada na Lei
de Boole, ambos os métodos descritos em (RICHARDS, 2002), obtivemos a expressão
das integrais como funções polinomiais:
Z
404 dt =
F
ini ((t))
(4t+101)2
c
d
Z
404 dt =
(F
ini ((t))+(t))
(4t+101)2
c
d
A variação do trabalho realizado pela partícula no
sentado na gura 5.6
Movimento 1 no gráco repre-
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
Figura 5.6: Gráco de
Rd
c
52
404 dt
F((t)) (4t+101)
2
Enquanto a partícula não utrapassa o meio da fenda, a força que atua na partícula
sofre uma redução devido ao campo elétrico da fenda, após o meio a força se estabiliza
pois a partícula, supostamente, não passa pelo campo. A variação do trabalho realizado
pela partícula no
Movimento 2 no gráco representado na gura 5.7
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
Figura 5.7: Gráco de
Rd
c
53
404 dt
F((t)) (4t+101)
2
Após ultrapassar o meio da fenda, a força que atua na partícula começa a crescer
em termos escalares, isso porque a partícula entra no campo elétrico da fenda, que a
partir desse ponto, é favorável ao movimento. Antes desse ponto, o trabalho é constante.
É possível notar que no
movimento 1 desdo início a partícula sofre uma retração do
seu movimento, devido ao campo elétrico, com isso máximo e o mínimo dos intervalos
que representam o trabalho realizado se tornam ainda maiores.
5.3.1
Considerações Finais sobre o Experimento
A trajetória indeterminada da partícula não é um problema para uma estimativa
do trabalho realizado. Por mais que se estime alguma trajetória, o valor do trabalho
sempre estará entre dois valores estimados como os extremos de um intervalo. Com isso
podemos concluir que pensar em um modelo de matemática intervalar para modelos
matemáticos para a mecânica quântica pode ser uma ferramenta poderosa para o de-
5.3 Modelagem Intervalar do Experimento de Difração de uma Partícula
54
senvolvimento desse ramo da física que por muitas vezes se depara com o problema da
incerteza dos valores atribuidos as variáveis.
55
6 Conclusões e Trabalhos Futuros
6.1
Conclusões
A matemática intervalar é uma alternativa para solucionar problemas onde existam
erros computacionais e erros de exatidão que se apresentam cotidianamente em computações numéricas. Embora a matemática intervalar seja uma alternativa para abordar
esse tipo de problema, ela também permite lidar com a incerteza na representação numérica dos valores de certos atributos, como o peso, a largura ou fenômenos da natureza,
de alguns objetos.
Contudo, a matemática intervalar (comparada com a matemática
clássica) é recente, por esta razão existem muitas denições e teorias da matemática
clássica que ainda não foram estendidas para a matemática intervalar.
No presente
trabalho é proposto uma integral de linha intervalar, que estende integral intervalar em
(BEDREGAL; BEDREGAL, 2010), assim como a integral de linha da matemática clássica de uma forma matematicamente bem fundamentada. Apresentamos, também, uma
aplicação desta integral de linha intervalar para calcular o trabalho realizado pela força
resultante em uma partícula de teste no experimento de difração de um elétron por uma
fenda. Sabendo que um dos problemas da mecânica quântica consiste em determinar o
valor que pode ser atribuido a uma variável considerando tanto, a incerteza do estado
da variável, como a incerteza da medição correta do seu valor, usamos um intervalo para
caracterizar a posição relativa e aproximada da partícula de tal maneira que o intervalo
contenha o real valor da variável.
Uma vez que o problema foi contextualizado, sob
a luz da matemática intervalar, foi utilizada a integral de linha intervalar, que graças
às características do sentido das forças que atuam sobre a partícula permite calcular o
trabalho que a partícula sofre durante parte do experimento, considerando a incerteza
do seu posicionamento. Utilizar a denição de intervalo para a valoração das variáveis
ao invés de valores pontuais pode levar a um outro caminho evolutivo para a mecâ-
6.2 Trabalhos Futuros
56
nica quântica, uma vez que a noção de intervalo permite englobar a idéia de valoração
da variável bem como a incerteza quanto ao estado. Assim podemos vislumbrar uma
gama de aplicações da matemática intervalar, e em particular, das integrais de linha
intervalares aqui propostas, em física quântica.
6.2
Trabalhos Futuros
Na matemática clássica um dos conceitos fundamentais é a noção de distância, em
particular, a de distância métrica. A análises real tem uma métrica que coincide com a
intuição geométrica de distância. Na matemática intervalar, foi o próprio Ramon Moore
( ) a qual tem sido amplamente
que, em (MOORE, 1979), propôs uma métrica para I R
aceita na comunidade de matemática intervalar, devido a que as pesquisas utilizando
essa métrica obtiveram importantes resultados além de que o próprio autor, provou que
essa métrica estende a métrica usual da reta. Contudo, essa noção de distância não é
uma função puramente intervalar, pois a imagem é um valor pontual e não um intervalo.
Ou seja, a distância entre dois intervalos é dado por uma valor exato. Mas, se pensamos
em intervalos como aproximações de números reais, então seria natural pensar que a
distância entre dois intervalos deve aproximar (conter), também, a distância entre os
valores reais que eles aproximam.
Isto, motivou (TRINDADE et al., 2009) a propor
uma extensão da noção de distância para distancia intervalares, e a propor uma tal
( )
distância intervalar para I R . Assim, como trabalho futuro pretendemos desenvolver
uma versão das integrais de linha intervalares que se base nessa, ou em outra, distância
intervalar.
As integrais de linha possuem aplicações fundamentais para diversas áreas cientícas. Contudo, muitas dessas aplicações fazem uso das integrais de linha em curvas fechadas e integrais curvilíneas (integrais de linha denidas de funções
F : I(R)n ! I(R)m).
Logo, seria interessante que existissem as fundamentações matemáticas da integral curvilínea bem como da integral curvilínea denida numa curva fechada em espaços intervalares.
57
Referências Bibliográcas
ACIOLY, B. M.
Fundamentação computacional da matemática intervalar. Tese
(Doutorado) Instituto de Informática, Universidade Federal do Rio Grande do Sul,
Porto Alegre, 1991.
ASHOKARAJ, I. et al. Sensor Based Robot Localisation and Navigation: Using
Interval Analysis and Extended Kalman Filter. Sendai, Japão, 2004.
BEDREGAL, B. R. C.; BEDREGAL, R. C. A Generalization of the Moore and Yang
Integral Approach. Computing, 2010. (submetido).
BEECHING, R.
Electron Diraction.
England:
Beeching Press, 2007. ISBN
978-1406765496.
BOYER, C. B.
The History of the Calculus and Its Conceptual Development. New
York: Dover, 1949.
CHANG, I.-C.; YU, C.-C.; LIOU, C.-T. Interval arithmetic approach to qualitative
physics: static systems.
International Journal of Intelligent Systems, v. 8, n. 3, p.
405430, mar. 1993. ISSN 0884-8173.
DARROW, K. K. Davisson and Germer.
Scientic American, v. 178, n. 5, maio 1948.
ISSN 0036-8733.
D'ESPAGNAT, B. The quantum theory and reality.
Scientic American, v. 241, n. 5,
p. 128140, nov. 1979. ISSN 0036-8733.
DOROGOVTSEV, A. A. An approach to the stochastic calculus in the non-gaussian
case. Hindawi Publishing Corporation, 1995. ISSN 10489533.
EISBERG, R.; RESNICK, R.
Quantum Physics of Atoms, Molecules, Solids,
Nuclei, an d Particles. Hoboken, NJ, USA: John Wiley and Sons, 1985.
FULKS, W.
Advanced Calculus. New York:
GUIDORIZZI, H. L.
John Wiley, 1969.
Um Curso de Cálculo. Rio de Janeiro, RJ, 1989. v. 3.
HALLIDAY, D.; RESNICK, R.
Fundamentos de Física. Rio de Janeiro, RJ: Wiley,
2007.
Path Integrals in Quantum Mechanics, Statistics, Polymer
Physics, and Financial Markets. New Jersey, USA: World Scientic Publishing
KLEINERT, H.
Company, 2004. ISBN 978-9812381071.
Referências Bibliográcas
KOLEV, L. V.
58
Interval Methods for Circuit Analysis. USA: World Scientic, 1993.
ISBN 9810214138.
KULISCH, U. W.; MIRANKER, W. L. The arithmetic of the digital computer: A new
approach.
SIAM Rev., v. 28, p. 140, 1986.
MENDOZA, R. et al. Injetividade do funcional Dirichlet-Neumann elítico via
matemática intervalar.
Revista TEMA, v. 10, n. 1, p. 3140, 2009.
MERLET, J.-P. Solving the Forward Kinematics of a Gough-Type Parallel Manipulator
with Interval Analysis.
I. J. Robotic Res, v. 23, n. 3, p. 221235, 2004. Disponível em:
<http://ijr.sagepub.com/cgi/content/abstract/23/3/221>.
MOORE, R. E.
Automatic error analysis in digital computation. Sunnyvale, CA,
USA, 1959.
MOORE, R. E.
Interval Analysis. Englewood Clis, NJ, 1966.
MOORE, R. E.
Methods and Applications of Interval Arithmetic. Philadelphia:
SIAM, 1979. (Studies in Applied Mathematics).
MOORE, R. E.; STROTHER, W.; YANG, C. T.
Interval Integrals. Sunnyvale, CA,
USA, 1960.
MOORE, R. E.; YANG, C. T.
RICHARDS, D.
Interval Analysis. Sunnyvale, CA, USA, 1959.
Advanced mathematical methods with Maple.
Cambridge, UK:
Cambridge University Press, 2002. xv + 862 p. ISBN 0-521-77010-6, 0-521-77981-2
(paperback).
Em direção a uma representação para equações algébricas
:uma lógica equacional local. Dissertação (Mestrado) Biblioteca Digital de Teses e
SANTOS, J. M. dos.
Dissertações da UFRN, jul. 17 2001.
SINGH, V.
Quantum Mechanics and Reality. dez. 20 2004.
SQUIRES, E.
The Mystery of the Quantum World. New York:
Oxford University
Press, 1993.
SUNAGA, T. Theory of an interval algebra and its application to numerical analysis.
RAAG Memoirs, v. 2, p. 2946, 547564, 1958.
SUNDQUIST, A. Dynamic line integral convolution for visualizing streamline
evolution.
em:
IEEE Trans. Vis. Comput. Graph, v. 9, n. 3, p. 273282, 2003. Disponível
<http://computer.org/tvcg/tg2003/v0273abs.htm>.
TRINDADE, R. M. et al. An interval metric.
Advanced Technologies,
I-Tech
Education and Publishing, Kirchengasse 43/3, A-1070 Vienna, Austria, 2009.
TRINDADE, R. M. P.
Uma Análise Intervalar de Scott. Dissertação (Mestrado) Departamento de Informática, Universidade Federal de Pernambuco-UFPE, 2009.