Matemática Básica 09 Trigonometria

Matemática Básica 09
Trigonometria
1. Introdução
A palavra Trigonometria tem por significado do grego “trigonon- triângulo” e “metron – medida”,
associada diretamente ao estudo dos ângulos e lados dos triângulos, figuras básicas em qualquer
estudo de geometria. A trigonometria é usada para resolver problemas geométricos que relacionam
ângulos e distâncias.
2. Classificação dos Triângulos quanto aos lados
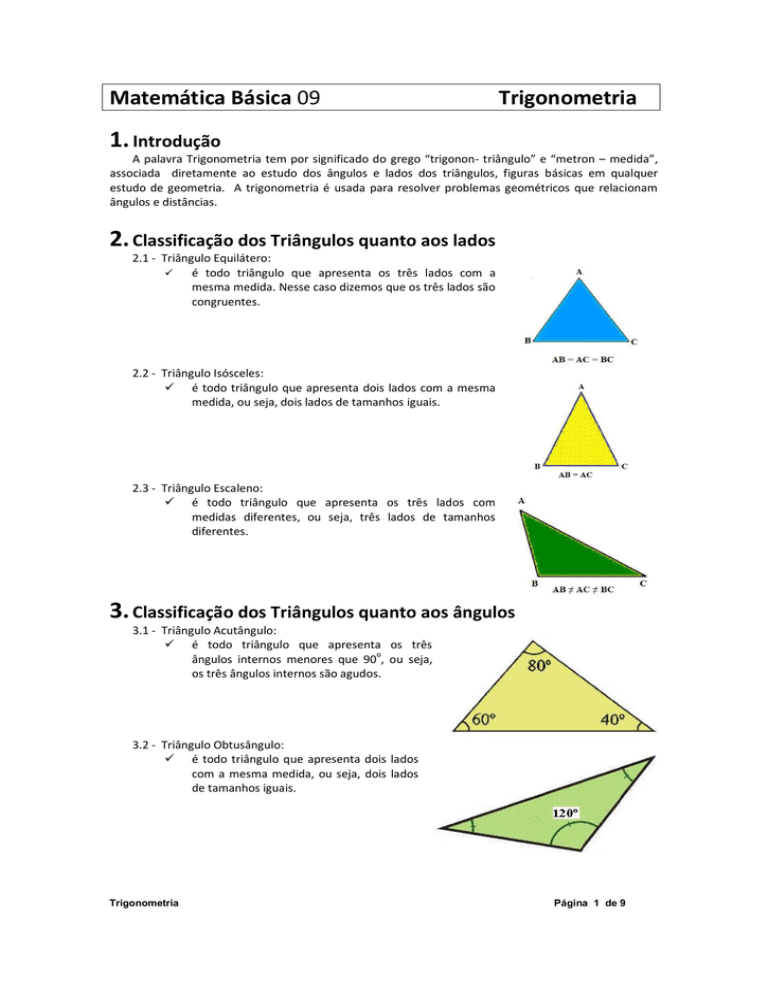
2.1 - Triângulo Equilátero:

é todo triângulo que apresenta os três lados com a
mesma medida. Nesse caso dizemos que os três lados são
congruentes.
2.2 - Triângulo Isósceles:
 é todo triângulo que apresenta dois lados com a mesma
medida, ou seja, dois lados de tamanhos iguais.
2.3 - Triângulo Escaleno:
 é todo triângulo que apresenta os três lados com
medidas diferentes, ou seja, três lados de tamanhos
diferentes.
3. Classificação dos Triângulos quanto aos ângulos
3.1 - Triângulo Acutângulo:
 é todo triângulo que apresenta os três
ângulos internos menores que 90o, ou seja,
os três ângulos internos são agudos.
3.2 - Triângulo Obtusângulo:
 é todo triângulo que apresenta dois lados
com a mesma medida, ou seja, dois lados
de tamanhos iguais.
Trigonometria
Página 1 de 9
3.3 - Triângulo Retângulo:
 é todo triângulo que apresenta um ângulo interno reto,
ou seja, que possui um ângulo medindo 90o.
4. Razões Trigonométricas
 Hipotenusa e catetos
Em um triângulo chamamos o lado oposto ao ângulo reto de hipotenusa e os lados adjacentes
de catetos. Observe a figura.
A figura representa um triângulo retângulo
AB e AC são catetos
BC é a hipotenusa (lado oposto ao ângulo reto – de 90º)

Seno, Cosseno e Tangente
Considere o triângulo retângulo BAC.
Tomando por base os elementos desse triângulo, podemos definir as seguintes razões
trigonométricas:
SENO : seno de um ângulo agudo é a razão entre
a medida do cateto oposto a esse ângulo e a
medida da hipotenusa.
Assim:
COSSENO : Cosseno de um ângulo agudo é
a razão entre a medida do cateto adjacente
a esse ângulo e a medida da hipotenusa.
Assim:
Trigonometria
Página 2 de 9
TANGENTE : Tangente de um ângulo agudo
é a razão entre a medida do cateto oposto
e a medida do cateto adjacente a esse
ângulo.
Assim:
Exemplo:
OBS:
(1) A tangente de um ângulo agudo pode ser definida como a razão entre seno deste ângulo e o seu
cosseno. Assim:
(2) A tangente de um ângulo agudo é um número real positivo.
(3) O seno e o cosseno de um ângulo agudo são sempre números reais positivos menores
que 1,
pois qualquer cateto é sempre menor que a hipotenusa.
Nunca esqueça do Teorema de Pitágoras, que diz “O QUADRADO DA HIPOTENUSA É IGUAL À
SOMA DOS QUADRADOS DOS CATETOS”. Assim, para o triângulo retângulo acima,
Trigonometria
a2 = b2 + c2.
Página 3 de 9
5. Razões Trigonométricas de 30º, 45º e 60º
Considere as figuras:
5.1 – Seno, Cosseno e Tangente de 30º
5.2 – Seno, Cosseno e Tangente de 45º
5.3 – Seno, Cosseno e Tangente de 60º
Trigonometria
Página 4 de 9
Resumindo:
6. Relação entre graus e radianos
Correspondência:
Exemplos:
1) Transformar 30º em radianos
Solução:
180º ------ π rad
30º ------- x
Logo: x = (30. π)/180 = π/6 rad
7. Círculo Trigonométrico
O círculo trigonométrico é uma circunferência de raio unitário com intervalo de [0, 2π], a cada
ponto da circunferência associamos um número real.
No círculo trigonométrico existem alguns ângulos notáveis, isto é, valores que estão presentes com
maior frequência em situações problemas. A tabela a seguir relaciona as unidades de medida, graus e
radianos.
Trigonometria
Página 5 de 9
No círculo trigonométrico trabalhamos três tipos de simetria: em relação ao eixo vertical (seno),
eixo horizontal (cosseno) e em relação ao centro.
7.1 - Seno
Alguns valores envolvendo seno de ângulos são conhecidos e fáceis de aprimorar, por exemplo, sen
π/6 = sen 30º = 1/2. Outro bem familiar é sen π/4 = sem 45º = √3/2. Para identificarmos o seno dos
outros ângulos utilizamos a SIMETRIA VERTICAL. Observe a circunferência trigonométrica a seguir:
7.2 - Cosseno
No caso dos cossenos vamos utilizar a SIMETRIA HORIZONTAL para determinar o cosseno dos
ângulos do círculo trigonométrico:
Trigonometria
Página 6 de 9
8. Sinais do Seno e do Cosseno X Círculo Trigonométrico
8.1 - Seno
e
Obs: O seno é positivo nos
8.2 - Cosseno
e
9. Exercícios
9.1 - Determine o valor de x na figura ao lado.
Solução: Em relação ao ângulo de 42º, o cateto de medida x é o cateto
oposto e 5cm é a hipotenusa. Desse modo, devemos usar o seno.
Assim,
Substituindo
o
valor
de
,
tem-se
que
9.2 – Uma mulher cujos olhos estão a 1,5 m do
solo, em um ângulo de 12º, um edifício que se
encontra a 200m dela. Qual é a altura
aproximada do edifício?
Solução: No triângulo da figura ao lado, temos:
Sendo
, teremos:
Esquematizando:
Assim:
Resposta: A altura aproximada do edifício é de
44 m.
Trigonometria
Página 7 de 9
9.3 – Observe o triângulo da figura ao lado. Sendo
o valor de x.
Solução: Como
, determinar
, teremos:
.
Usando o teorema de Pitágoras:
10.
Relações entre Razões Trigonométricas
Observe que, se representarmos por x a medida de um
ângulo agudo, a medida de seu complemento será
representado por 90º - x. Assim:
1)
2)
3)
4)
Exercício:
Trigonometria
Página 8 de 9
Trigonometria
Página 9 de 9