Matemática II

Matemática II
7
AULA
Prof. Sérgio Tambellini
Tabela de valores reais das razões trigonométricas
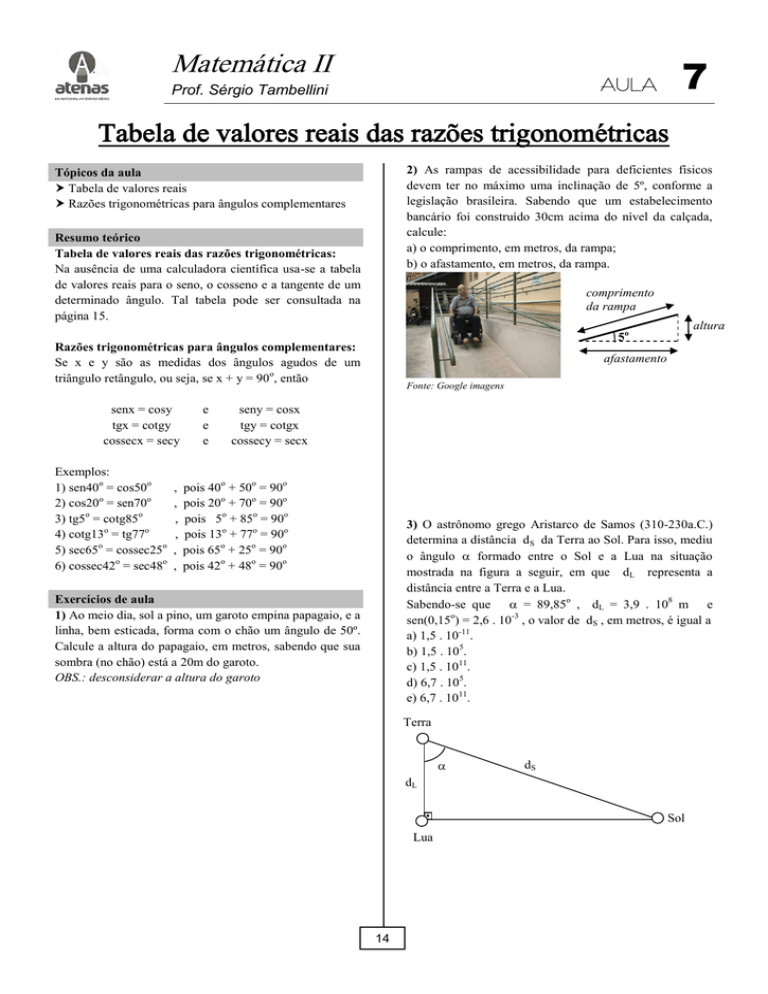
2) As rampas de acessibilidade para deficientes físicos
devem ter no máximo uma inclinação de 5º, conforme a
legislação brasileira. Sabendo que um estabelecimento
bancário foi construído 30cm acima do nível da calçada,
calcule:
a) o comprimento, em metros, da rampa;
b) o afastamento, em metros, da rampa.
Tópicos da aula
 Tabela de valores reais
 Razões trigonométricas para ângulos complementares
Resumo teórico
Tabela de valores reais das razões trigonométricas:
Na ausência de uma calculadora científica usa-se a tabela
de valores reais para o seno, o cosseno e a tangente de um
determinado ângulo. Tal tabela pode ser consultada na
página 15.
comprimento
da rampa
Razões trigonométricas para ângulos complementares:
Se x e y são as medidas dos ângulos agudos de um
triângulo retângulo, ou seja, se x + y = 90 o, então
senx = cosy
tgx = cotgy
cossecx = secy
Exemplos:
1) sen40o = cos50o
2) cos20o = sen70o
3) tg5o = cotg85o
4) cotg13o = tg77o
5) sec65o = cossec25o
6) cossec42o = sec48o
,
,
,
,
,
,
e
e
e
altura
5o
afastamento
Fonte: Google imagens
seny = cosx
tgy = cotgx
cossecy = secx
pois 40o + 50o = 90o
pois 20o + 70o = 90o
pois 5o + 85o = 90o
pois 13o + 77o = 90o
pois 65o + 25o = 90o
pois 42o + 48o = 90o
3) O astrônomo grego Aristarco de Samos (310-230a.C.)
determina a distância dS da Terra ao Sol. Para isso, mediu
o ângulo  formado entre o Sol e a Lua na situação
mostrada na figura a seguir, em que dL representa a
distância entre a Terra e a Lua.
Sabendo-se que  = 89,85o , dL = 3,9 . 108 m e
sen(0,15o) = 2,6 . 10-3 , o valor de dS , em metros, é igual a
a) 1,5 . 10-11.
b) 1,5 . 105.
c) 1,5 . 1011.
d) 6,7 . 105.
e) 6,7 . 1011.
Exercícios de aula
1) Ao meio dia, sol a pino, um garoto empina papagaio, e a
linha, bem esticada, forma com o chão um ângulo de 50º.
Calcule a altura do papagaio, em metros, sabendo que sua
sombra (no chão) está a 20m do garoto.
OBS.: desconsiderar a altura do garoto
Terra

dS
dL

Lua
14
Sol
Tabela de valores reais das razões trigonométricas
x
1o
2o
3o
4o
5o
6o
7o
8o
9o
10o
11o
12o
13o
14o
15o
16o
17o
18o
19o
20o
21o
22o
23o
24o
25o
26o
27o
28o
29o
30o
31o
32o
33o
34o
35o
36o
37o
38o
39o
40o
41o
42o
43o
44o
45o
sen x
0,0175
0,0349
0,0523
0,0698
0,0872
0,1045
0,1219
0,1392
0,1564
0,1736
0,1908
0,2079
0,2250
0,2419
0,2588
0,2756
0,2924
0,3090
0,3256
0,3420
0,3584
0,3746
0,3907
0,4067
0,4226
0,4384
0,4540
0,4695
0,4848
0,5000
0,5150
0,5299
0,5446
0,5592
0,5736
0,5878
0,6018
0,6157
0,6293
0,6428
0,6561
0,6691
0,6820
0,6947
0,7071
cos x
0,9998
0,9994
0,9986
0,9976
0,9962
0,9945
0,9925
0,9903
0,9877
0,9848
0,9816
0,9781
0,9744
0,9703
0,9659
0,9613
0,9563
0,9511
0,9455
0,9397
0,9336
0,9272
0,9205
0,9135
0,9063
0,8988
0,8910
0,8829
0,8746
0,8660
0,8572
0,8480
0,8387
0,8290
0,8192
0,8090
0,7986
0,7880
0,7771
0,7660
0,7547
0,7431
0,7314
0,7193
0,7071
x
46o
47o
48o
49o
50o
51o
52o
53o
54o
55o
56o
57o
58o
59o
60o
61o
62o
63o
64o
65o
66o
67o
68o
69o
70o
71o
72o
73o
74o
75o
76o
77o
78o
79o
80o
81o
82o
83o
84o
85o
86o
87o
88o
89o
tg x
0,0175
0,0349
0,0524
0,0699
0,0875
0,1051
0,1228
0,1405
0,1584
0,1763
0,1944
0,2126
0,2309
0,2493
0,2679
0,2867
0,3057
0,3249
0,3443
0,3640
0,3839
0,4040
0,4245
0,4452
0,4663
0,4877
0,5095
0,5317
0,5543
0,5774
0,6009
0,6249
0,6494
0,6745
0,7002
0,7265
0,7536
0,7813
0,8098
0,8391
0,8693
0,9004
0,9325
0,9657
1,0000
15
sen x
0,7193
0,7314
0,7431
0,7547
0,7660
0,7771
0,7880
0,7986
0,8090
0,8192
0,8290
0,8387
0,8480
0,8572
0,8660
0,8746
0,8829
0,8910
0,8988
0,9063
0,9135
0,9205
0,9272
0,9336
0,9397
0,9455
0,9511
0,9563
0,9613
0,9659
0,9703
0,9744
0,9781
0,9816
0,9848
0,9877
0,9903
0,9925
0,9945
0,9962
0,9976
0,9986
0,9994
0,9998
cos x
0,6947
0,6820
0,6691
0,6561
0,6428
0,6293
0,6157
0,6018
0,5878
0,5736
0,5592
0,5446
0,5299
0,5150
0,5000
0,4848
0,4695
0,4540
0,4384
0,4226
0,4067
0,3907
0,3746
0,3584
0,3420
0,3256
0,3090
0,2924
0,2756
0,2588
0,2419
0,2250
0,2079
0,1908
0,1736
0,1564
0,1392
0,1219
0,1045
0,0872
0,0698
0,0523
0,0349
0,0175
tg x
1,0355
1,0724
1,1106
1,1504
1,1918
1,2349
1,2799
1,3270
1,3764
1,4281
1,4826
1,5399
1,6003
1,6643
1,7321
1,8040
1,8807
1,9626
2,0503
2,1445
2,2460
2,3559
2,4751
2,6051
2,7475
2,9042
3,0777
3,2709
3,4874
3,7321
4,0108
4,3315
4,7046
5,1446
5,6713
6,3138
7,1154
8,1443
9,5144
11,4301
14,3007
19,0811
28,6363
57,2900
4) Durante um vendaval, um poste (vertical) de iluminação
quebrou-se em um ponto à certa altura do solo
(horizontal). A parte do poste acima da fratura inclinou-se
e sua extremidade superior encostou no solo a uma
distância de 4m da base dele e formando um ângulo de 50°
como o solo. Determine, em metros, a altura H do poste.
Dados: sen 50° = 0,77 , cos 50° = 0,64 e tg 50° = 1,20.
Tarefa de casa
1) Um avião levanta vôo de um aeroporto A, e sobe
fazendo um ângulo constante de 15° com a horizontal.
Determinar, em quilômetros, com aproximação de 2 casas
decimais, a altura do solo e qual a distância percorrida
quando passar pela vertical que passa por um prédio
situado a 2 quilômetros do ponto de partida A, ou seja
AP = 2km.
Dados:
sen15° = 0,2588; cos15° = 0,9659 e tg15° = 0,2679
y
H
y
x
15°
A
P
50°

4m
2) Um cabo de aço preso no chão (horizontal) e no topo de
uma torre (vertical) forma com o chão um ângulo de 70°,
como mostra a figura abaixo. Sabendo que o cabo de aço
foi fixado no chão a uma distância de 42m do pé da torre,
calcule, em metros, com aproximação de 2 casas decimais:
a) o comprimento do cabo de aço.
b) a altura da torre.
Dados:
sen70o = 0,9397
cos70o = 0,3420
tg70o = 2,7475
70°
Questão de raciocínio lógico:
Em um sistema de criptografia, as palavras são codificadas
de acordo com as seguintes regras:
 cada vogal deve ser substituída por um dentre os
números 1, 2, 3, 4 e 5 sendo que o 1 corresponde ao A, o 2
corresponde ao E, e assim por diante, conforme a ordem
em que as vogais aparecem no alfabeto;
 cada consoante deverá ser substituída pela letra
do alfabeto que a sucede. A letra Z será substituída
pela letra A.
Que palavra está codificada de acordo com esse sistema
criptográfico?
42m
3) A área de um polígono regular em função do apótema
é dada pela relação Apol
solo
n. .r
, onde n é o nº de lados

2
a)
b)
c)
d)
e)
do polígono regular , é o comprimento do lado e r o raio
da circunferência inscrita no polígono regular (apótema).
Usando as informações dadas anteriormente
calcule, em cm2, com aproximação de 2 casas decimais, a
área de um octodecágono regular (18 lados) em função da
medida do raio da circunferência inscrita (apótema),
sabendo que o lado do octodecágono regular mede 16cm.
Dados : sen10° = 0,1736
sen20° = 0,3420
cos10° = 0,9848
cos20° = 0,9397
tg10° = 0,1763
tg20° = 0,3640
16
Código
1A2EP
CS1R3M
D15R1
A2CSB
M2US1
Palavra
AZEDO
BRASIL
CAUSA
ZEBRA
LETRA