Métodos da falsa posição modificado e da secante
f(x)
y
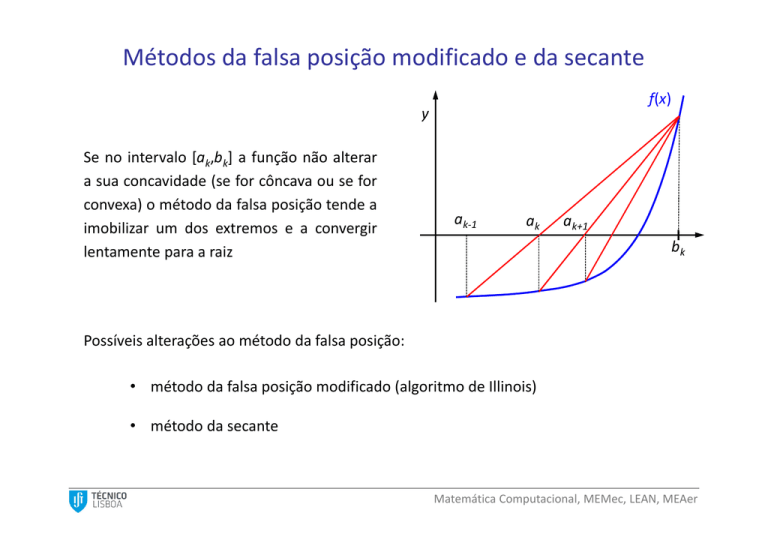
Se no intervalo [ak,bk] a função não alterar
a sua concavidade (se for côncava ou se for
convexa) o método da falsa posição tende a
imobilizar um dos extremos e a convergir
lentamente para a raiz
ak-1
ak
ak+1
bk
Possíveis alterações ao método da falsa posição:
• método da falsa posição modificado (algoritmo de Illinois)
• método da secante
Matemática Computacional, MEMec, LEAN, MEAer
Método da falsa posição modificado (algoritmo de Illinois)
f(x)
f(bk)
→ Se um dos extremos se mantiver
em duas iterações seguidas, então
dividir (sucessivamente) o valor da
função desse extremo por 2
f(bk)/2
ak-1
ak
xk+1
bk
f (bk ) ⋅ ak − f (ak ) ⋅ bk
xk +1 =
f (bk ) − f (ak )
xk +1 =
1
2
f (bk ) ⋅ ak − f (ak ) ⋅ bk
1
2 f (bk ) − f (ak )
Matemática Computacional, MEMec, LEAN, MEAer
Método da secante
f(x)
y
Formula de iteração
xk+1 = xk −
x–1
x1
f ( xk )
f [ xk−1 , xk ]
c/ f [ xk −1 , xk ] =
x2 x4
x0
x3
f (xk ) − f (xk −1 )
xk − xk−1
Modo alternativo de escrita
xk +1 =
f (xk ) ⋅ xk−1 − f (xk−1 ) ⋅ xk
f (xk ) − f (xk−1 )
• os pontos utilizados para traçar a secante são as duas últimas estimativas
• o intervalo pode não conter a raiz
• o método pode não convergir
• se convergir a ordem de convergência é de (1 + 5) / 2 = 1.618 (para zeros simples)
Matemática Computacional, MEMec, LEAN, MEAer












