1 Instrumentação Biomédica - Engenharia Biomédica » UFABC

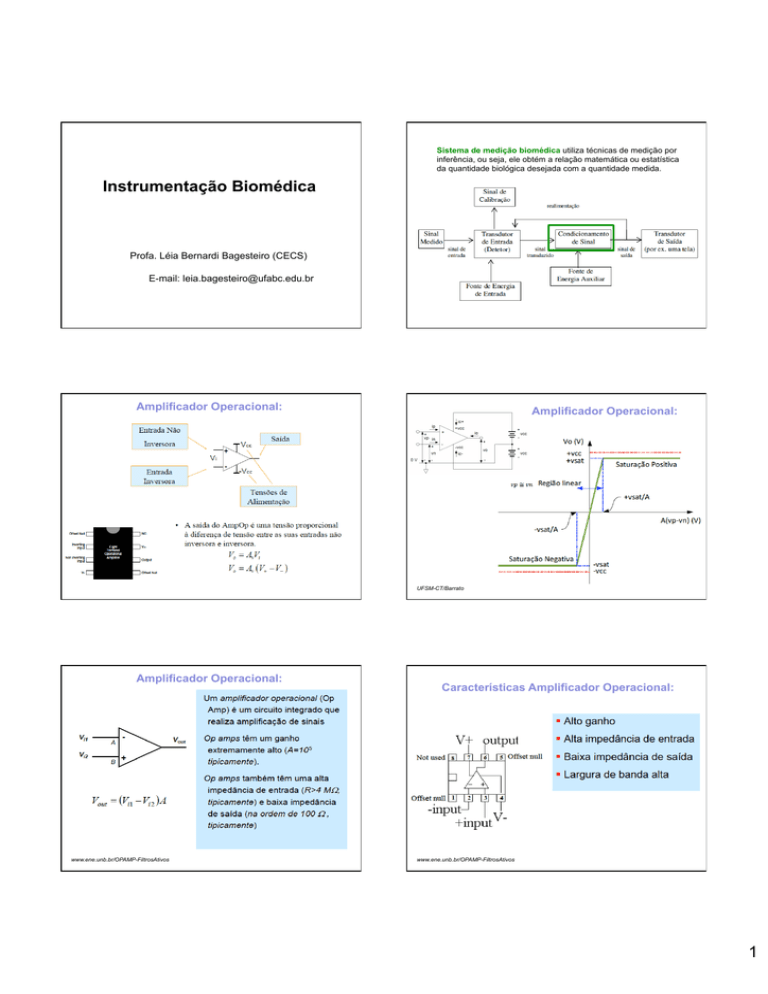
Sistema de medição biomédica utiliza técnicas de medição por
inferência, ou seja, ele obtém a relação matemática ou estatística
da quantidade biológica desejada com a quantidade medida.
Instrumentação Biomédica
Profa. Léia Bernardi Bagesteiro (CECS)
E-mail: [email protected]
Amplificador Operacional:
Amplificador Operacional:
UFSM-CT/Barrato
Amplificador Operacional:
www.ene.unb.br/OPAMP-FiltrosAtivos
Características Amplificador Operacional:
www.ene.unb.br/OPAMP-FiltrosAtivos
1
Amplificador Operacional real
ganho de malha aberta e fechada: resposta em frequência
Amplificador Inversor:
Malha aberta
Amf =1000
Amf =1
www.ene.unb.br/OPAMP-FiltrosAtivos
Amplificador Não-Inversor:
Amplificador inversor
8K2!
3K3!
ve
G="
-
8200
# "2,5
3300
vs
+
!
1K!
3
2
1
0
-1
Ve = cos t " Vs = #2,5cos t
-2
-3
0
5
10
15
20
25
30
35
www.ene.unb.br/OPAMP-FiltrosAtivos
!
OPAMP – Aplicação
Circuito integrador
Amplificador não inversor
ve
is
+
vs
-
ie
C
ve
-
R
vs
+
470!
68!
Ve
;
R
Ve
dVs
= "C
R
dt
1
Vs = "
# Vedt
RC
ie = is =
" 470 %
G = $1+
'(8
#
68 &
!
!
2
OPAMP – Aplicação
Circuito diferenciador (derivador)
is
Amplificador Diferencial:
R
ie
ve
C
vs
+
ie = is;
dVe
Vs
dVe
C
="
# Vs = "RC
dt
R
dt
www.ene.unb.br/OPAMP-FiltrosAtivos
!
OPAMP – Aplicação
Amplificador de instrumentação
ve1
+
R1
-
INA111 - Amplificador de instrumentação
R2
R
Rg
R
ve2
vs
+
R1
R2
+
Simetria 2AMPs não inversores " Z e # (e1,e2 )
Rg = R de controle de ganho
$ 2R ' R2
Vs = (Ve2 " Ve1 ) # &1" )
% Rg ( R1
!
!
Filtros Ativos:
Filtros
São associações elétricas que respondem a
variações de frequência, podendo atenuar – filtrar
determinadas frequências pré-estabelecidas.
Passivo: utiliza componentes do tipo resistivo, capacitivo e
indutivo.
Ativo: adiciona-se um amplificador.
Tipos:
-! passa-baixa
-! passa-alta
-! passa-banda
-! rejeita-banda
www.ene.unb.br/OPAMP-FiltrosAtivos
3
Filtros - Classificação
Filtros
Filtro Passa-Baixa RC (ativo)
Filtro Passa-Baixa RC (passivo)
fC =
1
2"RC
(Hz)
1
RC
(rad/s)
"C =
!
fC =
G=
www.ene.unb.br/OPAMP-FiltrosAtivos
!
Filtros
Filtros
Filtro Passa-Banda RC (passivo)
Filtro Passa Banda RC (ativo)
Filtro Passa-Alta RC (ativo)
fC =
fC =
1
2"RC
A primeira etapa deixa passar somente
freqüências maiores ou iguais a fC0 e
depois apenas as menores que fC1.
1
2"R1C
fC (Hz) =
"R
G= 2
R1
!
1
2"RC
!
!
f1 " f 2
1
2"R1C1
fC 2 (Hz) =
1
2"R2C2
G=
!
!
"R2
R1
!
Filtros
Filtro Rejeita Banda RC (ativo)
fC1 (Hz) =
!
fC =
!
Filtro Rejeita-Banda RC (passivo)
"R2
R1
!
!
Filtro Passa-Alta RC (passivo)
1
2"R2C
Filtros
Filtro Passivo Integrador
Filtro Ativo Integrador
Resposta de um filtro rejeita-banda ideal
4
Filtros: Características
Filtros
Filtro Passivo Diferenciador
Filtro Ativo Diferenciador
•!
•!
Filtros: Resposta em Freqüência
Ideal: banda linear, e descida acentuada na faixa de transição
Real: “rippling” entre a banda de passagem/parada e a de transição.
Filtros: Características
•! Capacitores influenciam na resposta em frequência do filtro.
•! Capacitores são adicionados para criar certas funções (e.g. integradores)
•! A ordem do filtro depende do número de elementos que armazenam
energia que são utilizados.
Primeira Ordem (passa-baixa)
•!
Segunda Ordem (rejeita-banda)
Com todas as especificações de banda, freqüência de corte é possível projetar um
filtro com uma função de transferência apropriada
Filtros
Amp. Não-inversor
Filtro passa-baixa
Filtros
Amp. Não-inversor
Filtro passa-alta
Amp. Inversor
Filtro passa-baixa
Amp. Inversor
Filtro passa-alta
5
Filtros
Filtros - Projeto
Amp. Inversor
Filtro passa-banda
Amp. Não-inversor
Filtro passa-banda
www.ene.unb.br/OPAMP-FiltrosAtivos
Filtros - Projeto
Projete filtros passa-baixas e passa-altas ativos nas
freqüências de corte de 10, 100, 500, 1000 e 5000Hz. Após
projetá-los faça os gráficos de resposta em freqüência para
cada um deles (com auxilio de um programa computacional,
e.g. MatLab.)
www.ene.unb.br/OPAMP-FiltrosAtivos
Sistema de aquisição de dados
•!
Filtros Digitais
Os filtros digitais apresentam as mesmas funções dos filtros
analógicos e são implementados através de rotinas de
programação.
Vantagens: flexibilidade, facilidade de uso com alteração
imediata da sua característica durante o desenvolvimento,
sem realizar a troca de componentes.
Sinal entrada: ECG + 10% ruído de 60Hz
Sinal filtrado: filtro analógico (Twin Tee)
De um modo geral, vale a regra: digitalize o mais cedo
possível e depois, trate o sinal computacionalmente.
FFT do ECG + 10% 60Hz signal
Espectro FFT do sinal após filtro (Twin Tee)
6
Sistema de aquisição de dados
•!
Conceitos gerais
Sistema de aquisição de dados é qualquer arranjo que
possibilite transformar sinais analógicos em sinais digitais
para que se possa realizar um processamento digital em
sistemas computacionais: microcontroladores,
computadores, entre outros.
1.!
2.!
3.!
circuito condicionador: filtros e proteção do sistema
circuito ADC: analog to digital converter
Unidade de processamento de sinais: processadores em
geral, FPGA: filtros digitais, FFT (Fast fourier transform),
Wavelet transform, modelagem matemática de sinais
(cálculos de parâmetros de interesse).
Sinal de ECG original
Sinal após filtro digital 1ra ordem
(entrada = sinal + 10% ruído 60Hz)
Sinal após filtro digital 2da ordem
(entrada = sinal + 10% ruído 60Hz)
Filtros Analógicos e Digitais
=>> INTEGRIDADE do SINAL
Sistema de aquisição de dados
•!
Frequência de amostragem fs
Teorema de Nyquist: A frequência de amostragem deve
ser, no mínimo, duas vezes a frequência máxima (fm) do
espectro de fourier do sinal analógico v(t).
Característica Butterworth
G=
Característica Butterworth
1
1+ " 2n
!
!! Filtro cuja resposta é plana, ou seja, não apresenta ondulações (“ripples”).
!! Filtro Butterworth Passa-baixa de 1ra ordem.
7
Característica Butterworth
Característica Butterworth
!! Filtro Butterworth Passa-baixa fornece resposta plana na
banda de passagem – (conversores de dados “anti-aliasing”).
!! Filtro Butterworth Passa-baixa com n = 1 a 5.
Característica Chebyshev
G=
Característica Chebyshev
1
1+ " 2
!
Polinômio Chebyshev
!! Filtros que apresentam a melhor resposta próxima a frequência de corte
(fornece “equiripple” na banda de resposta) quando comparados aos filtros
Butterworth.
Característica Chebyshev
!! Filtros usados onde a resposta em frequência é mais importante do que uma
amplificação constante.
!! Resposta em frequência de um filtro passa-baixa de 4ºordem (tipo I) Chebyshev
(com !=1).
Comparação de Características
* Todos filtros de 5ºordem (mesmo nº de coeficientes)
8
Característica Bessel
!! Filtros com resposta linear numa banda mais larga de frequência (>>>
decaimento constante >> transição otimizada) – porém G não é tão “plano” e
banda transição não tão acentuada.
Comparação de Características
!! Butterworth: otimização banda passagem (plana).
!! Tschebyscheff: acentua “descida” banda transição >> banda atenuação
!! Bessel: linearização da resposta de fase até fc.
Referências Bibliográficas
Verifique as diferentes características de filtros (Butterworth, Bessel,
Chebyshev) com as ferramentas disponíveis no LabVIEW.
* Balbinot e Brusamarello. Instrumentação e Fundamentos de Medidas. V.1 (e
V.2). LTC. 2006 e 2007.
* Webster, J. G. (ed.). Medical Instrumentation: Application and Design, 3rd
edition, John Wiley & Sons. 1998.
•! Enderle, J.D. Bioinstrumentation. 2006.
•! Karris, S.T. Eletronic Devices and Amplifier circuits with MAtLab Applic.
2005.
•! Sistemas de Medição Biomédica - Parte I
•! Spiegel, Murray, Análise de Fourier, Coleção Schaum, McGraw-Hill do Brasil,
São Paulo. 1976.
•! Kaplan,Wilfred, Cálculo Avançado, V.1 e 2. Edgard Blücher Editora e
EDUSP, São Paulo. 1972.
9