simulação e análise do crescimento tumoral baseado no

B.1.5 - Engenharia Elétrica
SIMULAÇÃO E ANÁLISE DO CRESCIMENTO TUMORAL BASEADO NO MODELO DE
KIRSCHNER E PANETTA
1
José G. S. Azevedo Junior *, Marcos P. R. Cabral¹, Allan D. F. Corrêa¹, Welton J. P. Santos¹, Matheus C. Silva¹,
Laercio B. Ferreira², Orlando F. Silva³.
1. Programa de Educação Tutorial de Engenharia Elétrica – UFPA; *[email protected].
2. Engenheiro Eletricista.
3. Orientador - Professor da Faculdade de Engenharia Elétrica – UFPA;
Palavras Chave: Câncer, sistema imunológico, antigenicidade.
Introdução
O câncer é uma das principais causas de morte no
mundo e ainda não se tem estudos conclusivos sobre sua
origem, desenvolvimento e mecanismos de tratamento.
Desta forma a modelagem matemática do problema e
simulação computacional tem se tornado uma ferramenta
importante para o estudo dos sistemas de atuação desta
enfermidade no organismo humano. O presente trabalho
se baseou no modelo matemático proposto em [3], que
descreve a ação do sistema imunológico frente a células
tumorais e possíveis entradas de tratamento através de
três equações diferenciais. Para efeito de simulação
alguns parâmetros do modelo foram obtidos noutras
referências além de [3], ulizou-se o Matlab e os resultados
obtidos foram comparados aos encontrados em [3] sendo
avaliada particularmente a influência da antigenicidade.
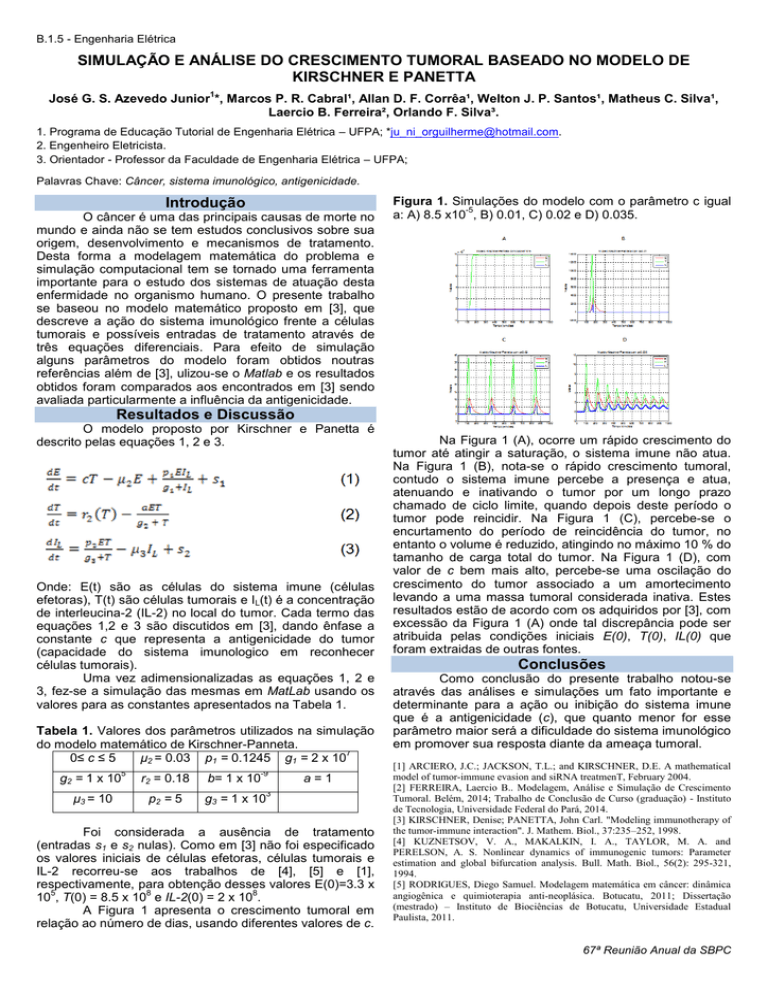
Figura 1. Simulações do modelo com o parâmetro c igual
-5
a: A) 8.5 x10 , B) 0.01, C) 0.02 e D) 0.035.
Resultados e Discussão
O modelo proposto por Kirschner e Panetta é
descrito pelas equações 1, 2 e 3.
Onde: E(t) são as células do sistema imune (células
efetoras), T(t) são células tumorais e IL(t) é a concentração
de interleucina-2 (IL-2) no local do tumor. Cada termo das
equações 1,2 e 3 são discutidos em [3], dando ênfase a
constante c que representa a antigenicidade do tumor
(capacidade do sistema imunologico em reconhecer
células tumorais).
Uma vez adimensionalizadas as equações 1, 2 e
3, fez-se a simulação das mesmas em MatLab usando os
valores para as constantes apresentados na Tabela 1.
Tabela 1. Valores dos parâmetros utilizados na simulação
do modelo matemático de Kirschner-Panneta.
7
0≤ c ≤ 5
µ2 = 0.03 p1 = 0.1245 g1 = 2 x 10
5
-9
g2 = 1 x 10
r2 = 0.18
b= 1 x 10
µ3 = 10
p2 = 5
g3 = 1 x 10
a=1
3
Foi considerada a ausência de tratamento
(entradas s1 e s2 nulas). Como em [3] não foi especificado
os valores iniciais de células efetoras, células tumorais e
IL-2 recorreu-se aos trabalhos de [4], [5] e [1],
respectivamente, para obtenção desses valores E(0)=3.3 x
5
8
8
10 , T(0) = 8.5 x 10 e IL-2(0) = 2 x 10 .
A Figura 1 apresenta o crescimento tumoral em
relação ao número de dias, usando diferentes valores de c.
Na Figura 1 (A), ocorre um rápido crescimento do
tumor até atingir a saturação, o sistema imune não atua.
Na Figura 1 (B), nota-se o rápido crescimento tumoral,
contudo o sistema imune percebe a presença e atua,
atenuando e inativando o tumor por um longo prazo
chamado de ciclo limite, quando depois deste período o
tumor pode reincidir. Na Figura 1 (C), percebe-se o
encurtamento do período de reincidência do tumor, no
entanto o volume é reduzido, atingindo no máximo 10 % do
tamanho de carga total do tumor. Na Figura 1 (D), com
valor de c bem mais alto, percebe-se uma oscilação do
crescimento do tumor associado a um amortecimento
levando a uma massa tumoral considerada inativa. Estes
resultados estão de acordo com os adquiridos por [3], com
excessão da Figura 1 (A) onde tal discrepância pode ser
atribuida pelas condições iniciais E(0), T(0), IL(0) que
foram extraidas de outras fontes.
Conclusões
Como conclusão do presente trabalho notou-se
através das análises e simulações um fato importante e
determinante para a ação ou inibição do sistema imune
que é a antigenicidade (c), que quanto menor for esse
parâmetro maior será a dificuldade do sistema imunológico
em promover sua resposta diante da ameaça tumoral.
[1] ARCIERO, J.C.; JACKSON, T.L.; and KIRSCHNER, D.E. A mathematical
model of tumor-immune evasion and siRNA treatmenT, February 2004.
[2] FERREIRA, Laercio B.. Modelagem, Análise e Simulação de Crescimento
Tumoral. Belém, 2014; Trabalho de Conclusão de Curso (graduação) - Instituto
de Tecnologia, Universidade Federal do Pará, 2014.
[3] KIRSCHNER, Denise; PANETTA, John Carl. "Modeling immunotherapy of
the tumor-immune interaction". J. Mathem. Biol., 37:235–252, 1998.
[4] KUZNETSOV, V. A., MAKALKIN, I. A., TAYLOR, M. A. and
PERELSON, A. S. Nonlinear dynamics of immunogenic tumors: Parameter
estimation and global bifurcation analysis. Bull. Math. Biol., 56(2): 295-321,
1994.
[5] RODRIGUES, Diego Samuel. Modelagem matemática em câncer: dinâmica
angiogênica e quimioterapia anti-neoplásica. Botucatu, 2011; Dissertação
(mestrado) – Instituto de Biociências de Botucatu, Universidade Estadual
Paulista, 2011.
67ª Reunião Anual da SBPC