Noções Básicas de Lógica Matemática e Teoria de Conjuntos

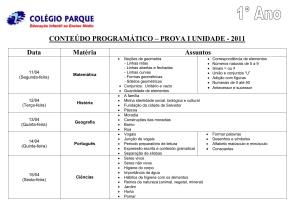
Álgebra Linear e Geometria Analı́tica
Engenharia Electrotécnica
Escola Superior de Tecnologia de Viseu
www.estv.ipv.pt/PaginasPessoais/lucas
[email protected]
2007/2008
Álgebra Linear e Geometria Analı́tica
Cap. 2 - Noções Básicas de Lógica Matemática e Teoria de Conjuntos
2.1 Proposições e Valores Lógicos
2.2 Operações Lógicas
2.3 Propriedades das Operações Lógicas
2.4 Conjuntos e Operações com Conjuntos
2.5 Produto Cartesiano
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.1 Proposições e Valores Lógicos
Proposição é uma expressão a respeito da qual faz sentido dizer se é
verdadeira ou falsa.
Cada proposição tem um e um só valor lógico, de entre dois
disponı́veis,
verdadeiro (V) ou falso (F)
Exemplos
−→
Viseu é uma cidade
Viseu é bonita
−→
sentimento de alguém)
Amanhã vou ao cinema −→ É uma proposição, que neste momento
não se pode dizer o seu valor lógico, mas pode-se dizê-lo amanhã
(ESTV)
Proposição verdadeira
Não é proposição (expressão de um
Álgebra Linear e Geometria Analı́tica
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2007/2008
3 / 19
2.1 Proposições e Valores Lógicos
A lógica que vamos estudar pressupõe os seguintes princı́pios:
Princı́pios Lógicos:
Princı́pio da não contradição
Uma proposição não pode ser verdadeira e falsa ao mesmo
tempo
Princı́pio do terceiro excluı́do
Uma proposição é verdadeira ou falsa
(ESTV)
Álgebra Linear e Geometria Analı́tica
2007/2008
4 / 19
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.2 Operações Lógicas
A partir de proposições elementares e utilizando as operações lógicas,
obtêm-se novas proposições (compostas).
Operações Lógicas
Negação
∼p
Conjunção
Disjunção
Implicação
p∧q
p∨q
p⇒q
Equivalência
p⇔q
Disjunção Exclusiva
p ∨˙ q
(ESTV)
não é verdade que p
não p
peq
p ou q
se p então q
p só se q
p é cond. suficiente para que q
q é cond. necessária para que p
p equivalente a q
p se e só se (sse) q
ou p ou q
Álgebra Linear e Geometria Analı́tica
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
p
antecedente
⇒
2007/2008
5 / 19
2.2 Operações Lógicas
q
consequente
Exemplos
Se estiver bom tempo e não estiver cansado vou à aula teórica de
Álgebra Linear.
9 ou 15 são ı́mpares mas não são primos.
É suficente ter 9.5 para passar a Álgebra Linear.
Estudar é condição necessária para a época de exames.
Um programa de computador funciona se e só se não tiver erros.
(ESTV)
Álgebra Linear e Geometria Analı́tica
2007/2008
6 / 19
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.2 Operações Lógicas
Tabelas de Verdade das Operações Lógicas:
Uma tabela de verdade faz corresponder aos possı́veis valores lógicos
das proposições o correspondente valor lógico da expressão
p
V
F
p
V
V
F
F
∼p
F
V
q
V
F
V
F
(ESTV)
p⇒q
V
F
V
V
p
V
V
F
F
q
V
F
V
F
p∧q
V
F
F
F
p
V
V
F
F
q
V
F
V
F
p∨q
V
V
V
F
p
V
V
F
F
q
V
F
V
F
p⇔q
V
F
F
V
p
V
V
F
F
q
V
F
V
F
p ∨˙ q
F
V
V
F
Álgebra Linear e Geometria Analı́tica
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2007/2008
7 / 19
2.3 Propriedades das Operações Lógicas
Propriedades da Negação, da Conjunção e da Disjunção:
p∨∼p≡V
p∧∼p≡F
p∨F ≡p
p∧V ≡p
p∨V ≡V
p∧F ≡F
p∨p ≡p
p∧p ≡p
∼ (∼ p) ≡ p
p∨q ≡q∨p
p∧q ≡q∧p
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r )
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r )
p ∨ (q ∧ r ) ≡ (p ∨ q) ∧ (p ∨ r )
p ∧ (q ∨ r ) ≡ (p ∧ q) ∨ (p ∧ r )
∼ (p ∨ q) ≡ ∼ p ∧ ∼ q
∼ (p ∧ q) ≡ ∼ p ∨ ∼ q
(ESTV)
Lei do terceiro excluido
Lei da contradição
Leis da identidade
Leis da absorção
Leis da idempotência
Lei da dupla negação
Leis da comutatividade
Leis da associatividade
Leis da distributividade
Leis de De Morgan
Álgebra Linear e Geometria Analı́tica
2007/2008
8 / 19
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.3 Propriedades das Operações Lógicas
Propriedades da Implicação e da Equivalência:
p ⇒q ≡∼p∨q
∼ (p ⇒ q) ≡ p ∧ ∼ q
p⇒q≡∼q⇒∼p
p ⇔ q ≡ (p ⇒ q) ∧ (q ⇒ p)
∼ (p ⇔ q) ≡ (p ∧ ∼ q) ∨ (q ∧ ∼ p)
(ESTV)
Relação da implicação
com a disjunção
Negação da implicação
Lei da conversão
Equivalência como conjunção
de implicações
Negação da equivalência
Álgebra Linear e Geometria Analı́tica
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2007/2008
9 / 19
2.3 Propriedades das Operações Lógicas
É possı́vel demonstrar todas estas propriedades recorrendo a tabelas
de verdade.
Exemplo (Prova da relação da implicação com a disjunção)
p ⇒q ≡∼p∨q
p
V
V
F
F
q
V
F
V
F
p⇒q
V
F
V
V
∼p
F
F
V
V
∼p∨q
V
F
V
V
Exercı́cio
Provar a equivalência como conjunção de implicações
p ⇔ q ≡ (p ⇒ q) ∧ (q ⇒ p)
(ESTV)
Álgebra Linear e Geometria Analı́tica
2007/2008
10 / 19
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.4 Conjuntos e Operações com Conjuntos
Axiomas
Axioma da Extensão: dois conjuntos são iguais se, e só se, têm
os mesmos elementos.
Axioma da Especificação: a cada conjunto A e a cada condição
S(x) corresponde um conjunto B cujos elementos são
exactamente os elementos de A para os quais S(x) acontece.
Escreve-se:
B = {x : x ∈ A e S(x)} ou B = {x ∈ A : S(x)}.
Exemplo
A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
(ESTV)
e
B = {x ∈ A : 2x < 9}.
Álgebra Linear e Geometria Analı́tica
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2007/2008
11 / 19
2.4 Conjuntos e Operações com Conjuntos
A ⊆ B ⇔ ∀x (x ∈ A ⇒ x ∈ B)
A = B ⇔ (A ⊆ B e B ⊆ A)
Conjunto Vazio
Conjunto Universal
∅, {}
E
Operações entre Conjuntos
Intersecção
Reunião
Complementação
Diferença
(ESTV)
∩
∪
.c
−
x
x
x
x
∈A∩B ⇔x ∈A∧x ∈B
∈A∪B ⇔x ∈A∨x ∈B
∈ Ac ⇔ ∼ (x ∈ A)
∈ A − B ⇔ x ∈ A ∩ B c ⇔ x ∈ A ∧ ∼ (x ∈ B)
Álgebra Linear e Geometria Analı́tica
2007/2008
12 / 19
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.4 Conjuntos e Operações com Conjuntos
Exemplo (1)
E = {números inteiros positivos não superiores a 10}
A = {x ∈ N : x é múltiplo de 3 e x não excede 9}
B = {números inteiros positivos inferiores a 6}
E = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {3, 6, 9}
B = {1, 2, 3, 4, 5}
Ac = {1, 2, 4, 5, 7, 8, 10}
A ∩ B = {3}
A ∪ B = {1, 2, 3, 4, 5, 6, 9}
A − B = {6, 9}
(ESTV)
Álgebra Linear e Geometria Analı́tica
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2007/2008
13 / 19
2.4 Conjuntos e Operações com Conjuntos
Exemplo (2)
A = {a, b} e B = {a}
A ∩ B = {a}
A∪B =A
A − B = {b}
B − A = {}
Relação entre Conjuntos e Operações Lógicas
Identidade
Inclusão
Intersecção
Reunião
Complementação
(ESTV)
Equivalência
Implicação
Conjunção
Disjunção
Negação
Álgebra Linear e Geometria Analı́tica
2007/2008
14 / 19
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.4 Conjuntos e Operações com Conjuntos
Propriedades dos Conjuntos
A ∪ Ac = E
A ∩ Ac = ∅
A ∪ ∅ = A; A ∩ E = A
A ∪ E = E; A ∩ ∅ = ∅
A ∪ A = A; A ∩ A = A
(Ac )c = A
A ∪ B = B ∪ A; A ∩ B = B ∩ A
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
(A ∪ B)c = Ac ∩ B c
(A ∩ B)c = Ac ∪ B c
(ESTV)
Lei da complementação
Lei da exclusão
Leis da identidade
Leis da absorção
Leis da idempotência
Lei da dupla complementação
Leis da comutatividade
Leis da associatividade
Leis da distributividade
Leis de De Morgan
Álgebra Linear e Geometria Analı́tica
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2007/2008
15 / 19
2.4 Conjuntos e Operações com Conjuntos
Exercı́cio
Mostrar que:
(A − B) ∩ (A − C) = A − (B ∪ C);
A ∩ (Ac ∪ B) = A ∩ B.
Conjuntos Disjuntos
Dois conjuntos A e B dizem-se disjuntos se A ∩ B = ∅.
Dados conjuntos Ai , i ∈ I, dizem-se disjuntos dois a dois se para
quaisquer i, j ∈ I, com i = j se tem Ai ∩ Aj = ∅ .
Exemplo
{2, 3, 4}, {5, 6, 7}, {8, 9, 10} são disjuntos dois a dois.
(ESTV)
Álgebra Linear e Geometria Analı́tica
2007/2008
16 / 19
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.4 Conjuntos e Operações com Conjuntos
Cardinal de um Conjunto
O cardinal de um conjunto é igual ao número de elementos do
conjunto.
Notação: #A, card(A) ou | A |
Exemplo
A = {1, 3, 5, 6, 5, 8, 1, 2}
card(A) = 6
card(A ∪ B) = card(A)+ card(B)− card(A ∩ B);
Se A1 , A2 , . . . , An forem disjuntos dois a dois
card(A1 ∪ A2 . . . ∪ An ) = card(A1 )+ card(A2 ) + . . . + card(An ).
(ESTV)
Álgebra Linear e Geometria Analı́tica
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2007/2008
17 / 19
2.5 Produto Cartesiano
Produto Cartesiano
O produto cartesiano de A por B, designa-se por A × B e é dado
por:
A × B = {(a, b) : a ∈ A ∧ b ∈ B}
O produto cartesiano de n conjuntos é definido da forma:
A1 ×A2 ×. . .×An = {(a1 , a2 , . . . , an ) : a1 ∈ A1 ∧a2 ∈ A2 ∧. . .∧an ∈ An }
An = A × A × . . . × A
Se A1 , A2 , . . . , An são conjuntos finitos então:
card(A1 × A2 × . . . × An ) = card(A1 ) × card(A2 ) × . . . × card(An )
(ESTV)
Álgebra Linear e Geometria Analı́tica
2007/2008
18 / 19
Cap. 2 Noçoes Basicas de Logica Matematica e Teoria de
Conjuntos
2.5 Produto Cartesiano
Exemplo
A = {a, b} e B = {1, 2, 3}
A × B = {(a, 1), (b, 1), (a, 2), (b, 2), (a, 3), (b, 3)}
Conjunto Potência
Seja A um conjunto.
O conjunto potência de A ou o conjunto das partes de A designa-se
por P(A) ou 2A , e é o conjunto formado por todos os subconjuntos de
A.
Se A é finito então card(2A ) = 2card(A)
Exemplo
A = {a, b, c}
(ESTV)
2A = {∅, {a}, {b}, {c}, {a, b}, {a, c}, {c, b}, {a, b, c}}
Álgebra Linear e Geometria Analı́tica
2007/2008
19 / 19