Capacitor e Indutor em CA - Engenharia Eletrica

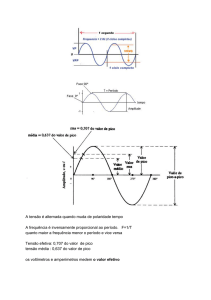
MI
MINISTÉRIO DA EDUCAÇÃO
UNIVERSIDADE FEDERAL DO PARANÁ
SETOR DE TECNOLOGIA
DEPARTAMENTO DE ENGENHARIA ELÉTRICA
TE216 - Laboratório de Eletrônica II
Prof. Alessandro L. Koerich
Experimento 4 – Análise de Circuitos
Capacitor e Indutor em CA
Objetivo
Verificar a variação da reatância capacitiva e da reatância indutiva com a frequência.
Componentes e Instrumentação





Capacitor cerâmico ou Poliéster 100nF (104).
Indutor (micro-choque de RF) 1mH.
Resistor 1kΩ.
Osciloscópio Digital de Dois Canais e Ponteiras 10x e 1x
Gerador de Funções
Capacitor em CA
Um capacitor, quando percorrido por uma corrente elétrica alternada, oferece uma oposição à passagem dela,
imposta por campo elétrico, denominada reatância capacitiva. Essa reatância capacitiva é inversamente
proporcional à frequência da corrente, ao valor do capacitor e é dada pela relação:
Podemos traçar o gráfico da reatância capacitiva em função da frequência, obtendo com resultado a curva
mostrada abaixo.
Do gráfico concluímos que, a medida que a frequência aumenta, a reatância
capacitiva decresce até atingir um valor praticamente nulo.
Como a reatância capacitiva é função da frequência, devemos medi-la por um
processo experimental, ou seja, aplicamos uma tensão alternada aos terminais
do capacitor, medimos o valor da tensão e da corrente, obtendo assim o seu
valor pela relação:
Aplicando uma tensão alternada nos terminais de um capacitor, como mostra o circuito da figura abaixo, surgirá
uma corrente alternada, pois o capacitor irá carregar-se e descarregar-se continuamente em função da
característica dessa tensão.
Lembrando que quando o capacitor está descarregado (VC = 0), a corrente
é máxima e quando carregado (VC = Vmáx ), a corrente é nula, podemos em
função disso representar graficamente essa situação, conforme mostra a
figura abaixo.
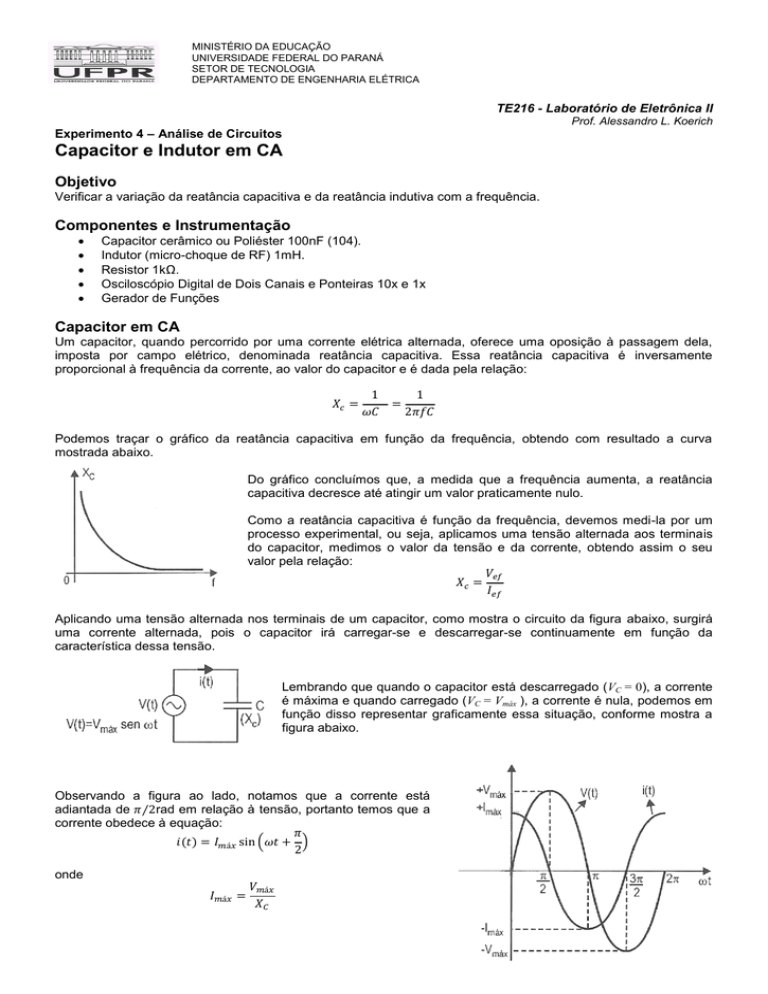
Observando a figura ao lado, notamos que a corrente está
adiantada de ⁄ rad em relação à tensão, portanto temos que a
corrente obedece à equação:
( )
onde
(
)
Indutor em CA
Um indutor, quando percorrido por uma corrente elétrica alternada, oferece uma oposição à passagem dela,
imposta por campo magnético, denominada reatância indutiva. Essa reatância indutiva é diretamente proporcional
à frequência da corrente, ao valor do indutor e é dada pela relação:
Podemos traçar o gráfico da reatância indutiva em função da frequência, obtendo
com resultado a curva mostrada ao lado. Do gráfico podemos concluir que a
reatância indutiva aumenta com a frequência.
Como a reatância indutiva é função da frequência, devemos medi-la por um
processo experimental, ou seja, aplicamos uma tensão alternada aos terminais do
indutor, medimos o valor da tensão e da corrente, obtendo assim o seu valor pela
relação:
Aplicando uma tensão alternada nos terminais de um indutor, como mostra o circuito da figura abaixo, surgirá uma
corrente alternada, pois o indutor irá energizar-se e desenergizar-se continuamente em função da característica
dessa tensão.
Lembrando que quando o indutor está energizado (VL = 0), a corrente é
máxima e negativa, e quando o indutor está desenergizado (VL = Vmáx ), a
corrente é nula, podemos em função disso representar graficamente essa
situação, conforme mostra a figura abaixo.
Observando a figura ao lado, notamos que a corrente está
atrasada de ⁄ rad em relação à tensão, portanto temos que a
corrente obedece à equação:
( )
(
)
onde
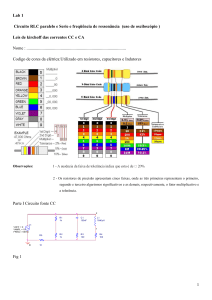
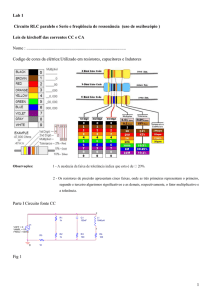
Parte Prática – Circuito RC
1) Monte o circuito da figura ao lado. Ajuste a frequência do gerador de sinais
para 10kHz.
2) Ajuste a tensão do gerador de sinais para obter no resistor as tensões
marcadas no quadro abaixo. Para cada caso, meça e anote a tensão pico a
pico no capacitor. Calcule os demais valores.
VRpp (V)
VRef (V)
Ief (mA)
VCpp (V)
VCef (V)
XC (Ω)
10
14
16
3) Ajuste o gerador de sinais para 10V pico a pico, mantendo-a constante a cada medida. Varie a frequência
de acordo com o quadro abaixo. Meça e anote para cada caso o valor da tensão pico a pico no resistor e
no capacitor. Calcule os demais valores.
f (kHz)
1
3
5
7
9
10
4) Calcule
VRpp(V)
VRef(V)
VCpp(V)
VCef(V)
Ief(mA)
XC(Ω)
e compare com os valores obtidos na tabela do item 2).
5) Com os valores obtidos na tabela do item 3), construa o gráfico XC = f(f).
Parte Prática – Circuito RL
6) Monte o circuito da figura acima. Ajuste a frequência do gerador de sinais para
100kHz.
7) Ajuste a tensão do gerador de sinais para obter no resistor as tensões
marcadas no quadro abaixo. Para cada caso, meça e anote a tensão pico a pico
no indutor. Calcule os demais valores.
10
VRpp (V)
14
16
VRef (V)
Ief (mA)
VLpp (V)
VLef (V)
XL (Ω)
8)
Ajuste o gerador de sinais para 10V pico a pico, mantendo-o constante a cada medida. Varie a frequência de
acordo com o quadro abaixo. Meça e anote para cada caso o valor da tensão pico a pico no resistor e no
indutor. Calcule os demais valores.
f (kHz)
VRpp(V)
VRef(V)
VLpp(V)
VLef(V)
10
30
50
70
90
100
9) Calcule
e compare com os valores obtidos no quadro do item 2).
10) Com os valores do quadro do item 3), construa o gráfico XL = f(f).
Ief(mA)
XL(Ω)