Cálculo Numérico

Cálculo Numérico
Faculdade de Ciências Sociais Aplicadas e Comunicação – FCSAC
Faculdade de Engenharia, Arquiteturas e Urbanismo – FEAU
Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia)
REVISÃO DA 2ª PARTE DO CURSO
1 – Interpolação polinomial
a. Método direto (resolução de sistema de equações)
b. Método de Lagrange (calculando os fatores de Lagrange)
c. Método de Newton (calculando os operadores diferenças dividas)
2 – Ajuste de Funções pelo método dos mínimos quadrados (MMQ)
a. Caso discreto
3 – Integração numérica
a. regra do trapezio
b. regra do trapézio repetida
c. regra 1/3 de Simpson
d. regra 1/3 de Simpson repetida
3 – Métodos numéricos para resolver eq. diferenciais ordinárias (EM PREPARAÇÃO)
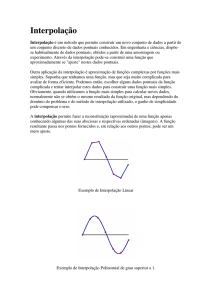
1 – Interpolação polinomial
Um polinômio de ordem n é escrito como:
n
Pn ( x ) = ∑ a k x k = a0 + a1 x + a 2 x 2 + a3 x 3 + .... + a n x n
k =0
a. Método direto
Nos nós da interpolação teremos sempre
Pn ( xk ) = f ( xk ) = yk
onde k = 0,1, 2, 3, 4, ..., n
Escrevendo essa condição para todos os pontos xk teremos n equações e n incógnitas que serão as constantes do
polinômio ( a0 , a1 , a 2 , a 3 ,...., a n ). Para encontrar essas constantes temos que resolver o sistema de equação
utilizando ou método direto de eliminação de Gauss (triangulariazação) ou algum método iterativo (GaussJacobi ou Gauss-Seidel)
1
b. Forma de Lagrange
Na forma de Lagrange o polinômio de ordem n pode ser escrito por:
n
Pn ( x ) = ∑ f ( x k ) Lk ( x ) = f ( x0 ) L0 ( x ) + f ( x1 ) L1 ( x ) + .... + f ( x n ) Ln ( x )
k =0
onde Lk(x) são equações de x conhecidas como fatores de Lagrange. Podem ser calculados a partir da formula
recursiva a baixo:
n
∏ (x − x )
Lk ( x ) =
j
j =0
j≠k
n
∏ (x
j =0
j≠k
k
− xj)
b. Forma de Newton
Na forma de Newton o polinômio de ordem n pode ser escrito por:
n
Pn ( x ) = f [ x0 ] + ∑ f [ x0 ,..., xk ]( x − x0 )...( x − xk −1 ) =
k =1
= f [ x0 ] + f [ x0 , x1 ]( x − x0 ) + f [ x0 , x1 , x2 ]( x − x0 )( x − x1 ) + f [ x0 , x1 , x2 , x3 ]( x − x0 )( x − x1 )( x − x2 ) +
+ .... + f [ x0 , x1 , x2 , x3 ,.... xn ]( x − x0 )( x − x1 )( x − x2 )( x − x3 )....( x − xn −1 )
onde f[xk] são números calculados a partir da tabela de pontos (x, f(x)) que se quer interpolar. Estes fatores são
conhecidos como operadores diferenças divididas e são determinados pela regra geral abaixo:
f[xi] ≡ f(xi)
Ex.
e
f[x0]=f(x0)
2
2 – Método dos mínimos quadrados
Sejam m pares de pontos oriundos de uma função f(x). Queremos encontrar uma função ϕ(x) tal que:
n
f ( x ) ≈ φ ( x ) = ∑ ai gi ( x ) = a1 g1 ( x ) + a2 g 2 ( x ) + a3 g 3 ( x )... + an g n ( x )
n∈Ι
i =1
As funções gi(x) são funções de qualquer tipo escolhidas para tentar ajustar o conjunto de dados experimentais,
por exemplo, a partir da análise dos diagrama de dispersão (gráfico dos pontos experimentais).
a1 , a2 , a3 ,...., an são os coeficientes das funções gi(x) e vão dar o peso de cada uma delas na equação ϕ(x).
⎛ n
⎞
d ⎜ ∑ ( f ( xk ) − φ ( xk )) 2 ⎟
No método dos mínimos quadrados temos a seguinte condição: ⎝ k =1
⎠ =0
da j
j = 1,2,3...n
Segundo essa condição, para encontrarmos a função ϕ(x) (dentre as escolhidas previamente) que melhor ajusta
os pontos experimentais utilizando o método MMQ teremos que resolver um sistema de n equações e n
incógnitas a1 , a2 , a3 ,...., an . Na forma matricial esse sistema pode ser escrito como
Aˆ × aˆi = bˆi ,
ou ainda:
m= num. de pontos experimentais
⎛ a11
⎜
⎜ a21
⎜ ...
⎜⎜
⎝ a n1
a12
a22
...
an 2
... a1n ⎞ ⎛ a1 ⎞ ⎛ b1 ⎞
⎟ ⎜ ⎟ ⎜ ⎟
... a2 n ⎟ ⎜ a2 ⎟ ⎜ b2 ⎟
×
=
... ... ⎟ ⎜ ... ⎟ ⎜ ... ⎟
⎟⎟ ⎜⎜ ⎟⎟ ⎜⎜ ⎟⎟
... ann ⎠ ⎝ an ⎠ ⎝ bn ⎠
m
onde
aij = ∑ g i ( xk ) g j ( xk ) =a ji
k =1
m
bi = ∑ f ( xk ) g i ( xk )
k =1
Para encontrar essas incógnitas e, portanto, escrever a função que melhor ajusta os pontos experimentais pelo
método dos mínimos quadrados, temos que resolver o sistema de equações utilizando o método direto de
eliminação de Gauss (triangulariazação) ou algum método iterativo (Gauss-Jacobi ou Gauss-Seidel).
Exemplos de funções ϕ (x) típicas:
- Para ajustar os pontos a uma reta temos
ϕ (x) = a1 + a2 x→ g1(x) = 1 e g2(x) = x
Sistema com 2 eqs.!
- Para ajustar os pontos a uma parábola temos
ϕ (x) = a1 + a2 x + a3x2 → g1(x) = 1 , g2(x) = x e g3(x) = x2
Sistema com 3 eqs.!
- Para ajustar os pontos a com uma função exponencial simples temos
ϕ (x) = a1 ex → g1(x) = ex
1 única equação!
3
2 – Interpolação Numérica
a. Regra do trapézio → f(x) ≈ p1(x)
h=(b-a)
primeira integral → ITR=37,8181; ETR ≤ 6; n=619
ET ≤
( b − a )3
max f ´´( x )
12 x∈[ a ,b ]
primeira integral → ITR=37,8181; ETR ≤ 6; n=619
b. Regra do trapézio repetida
=ITR
h=(b-a)/n
h=(b-a)/n
c. Regra 1/3 de Simpson → f(x) ≈ p2(x)
=IS
h=(b-a)/2
h=(b-a)/2
c. Regra 1/3 de Simpson repetida
=ISR
h=(b-a)/2n
h=(b-a)/2n
m=2n
n=m/2 é a metade de subdivisões do intervalo [a,b]
4