Simuladão de Física - NS Aulas Particulares

Simuladão de Física
1. (Ufrgs 2015) Em 2014, comemoraram-se os 50 anos do início da operação de trens de alta
velocidade no Japão, os chamados trens-bala. Considere que um desses trens desloca-se com
uma
velocidade constante de 360km / h sobre trilhos horizontais. Em um trilho paralelo, outro trem
desloca-se também com velocidade constante de 360km / h, porém em sentido contrário.
Nesse caso, o módulo da velocidade relativa dos trens, em m / s. é Igual a
a) 50.
b) 100.
c) 200.
d) 360.
e) 720.
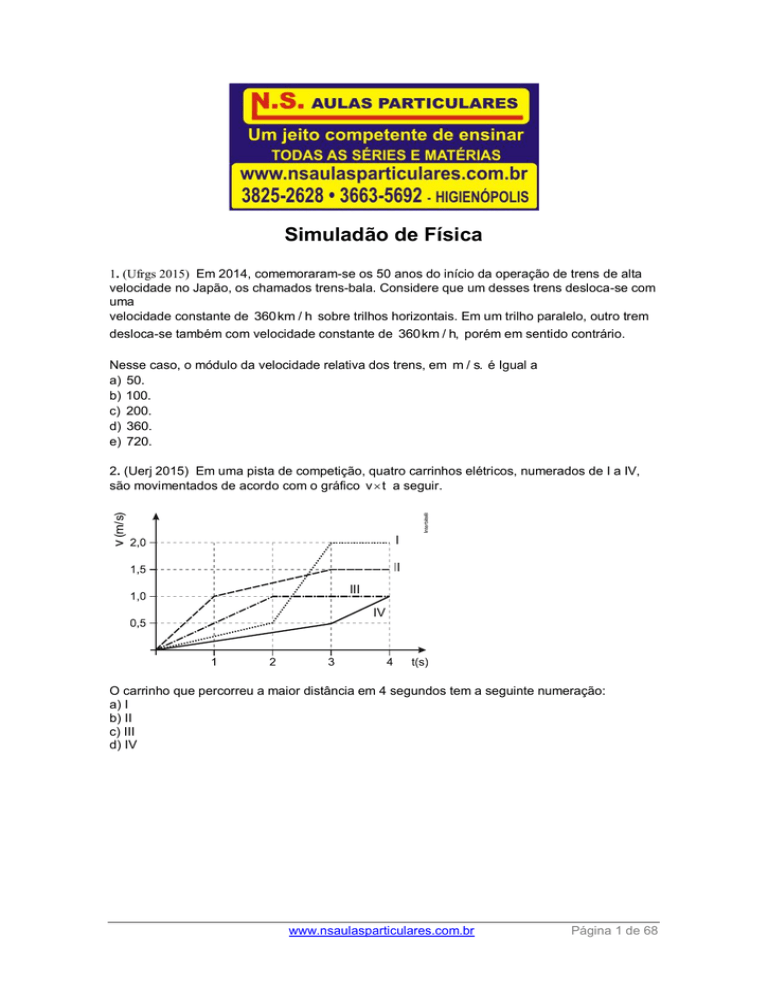
2. (Uerj 2015) Em uma pista de competição, quatro carrinhos elétricos, numerados de I a IV,
são movimentados de acordo com o gráfico v  t a seguir.
O carrinho que percorreu a maior distância em 4 segundos tem a seguinte numeração:
a) I
b) II
c) III
d) IV
www.nsaulasparticulares.com.br
Página 1 de 68
3. (G1 - cps 2015)
Se hoje um filme pode ser armazenado na forma de um arquivo digital, no passado, ele só
podia existir na forma de rolos, contendo uma grande quantidade de fotogramas, conforme
figura. Para causar a impressão de continuidade, esses fotogramas eram projetados um por
um, a uma velocidade de 24 fotogramas por segundo.
Se a cada 30mm da fita de um filme existe um único fotograma, em uma animação de 3
minutos de duração, a fita terá um comprimento aproximado, em metros, de
a) 70.
b) 90.
c) 130.
d) 150.
e) 220.
4. (Uemg 2015) O tempo é um rio que corre. O tempo não é um relógio. Ele é muito mais do
que isso. O tempo passa, quer se tenha um relógio ou não.
Uma pessoa quer atravessar um rio num local onde a distância entre as margens é de 50 m.
Para isso, ela orienta o seu barco perpendicularmente às margens.
Considere que a velocidade do barco em relação às águas seja de 2,0m / s e que a
correnteza tenha uma velocidade de 4,0m / s.
Sobre a travessia desse barco, assinale a afirmação CORRETA:
a) Se a correnteza não existisse, o barco levaria 25 s para atravessar o rio. Com a correnteza,
o barco levaria mais do que 25 s na travessia.
b) Como a velocidade do barco é perpendicular às margens, a correnteza não afeta o tempo de
travessia.
c) O tempo de travessia, em nenhuma situação, seria afetado pela correnteza.
d) Com a correnteza, o tempo de travessia do barco seria menor que 25 s, pois a correnteza
aumenta vetorialmente a velocidade do barco.
www.nsaulasparticulares.com.br
Página 2 de 68
5. (Ufrgs 2015) Trens MAGLEV, que têm como princípio de funcionamento a suspensão
eletromagnética, entrarão em operação comercial no Japão, nos próximos anos. Eles podem
atingir velocidades superiores a 550km / h. Considere que um trem, partindo do repouso e
movendo-se sobre um trilho retilíneo, é uniformemente acelerado durante 2,5 minutos até
atingir 540km / h.
Nessas condições, a aceleração do trem, em m / s2 , é
a) 0,1.
b) 1.
c) 60.
d) 150.
e) 216.
6. (G1 - cps 2015) Em um antigo projetor de cinema, o filme a ser projetado deixa o carretel F,
seguindo um caminho que o leva ao carretel R, onde será rebobinado. Os carretéis são
idênticos e se diferenciam apenas pelas funções que realizam.
Pouco depois do início da projeção, os carretéis apresentam-se como mostrado na figura, na
qual observamos o sentido de rotação que o aparelho imprime ao carretel R.
Nesse momento, considerando as quantidades de filme que os carretéis contêm e o tempo
necessário para que o carretel R dê uma volta completa, é correto concluir que o carretel F
gira em sentido
a) anti-horário e dá mais voltas que o carretel R.
b) anti-horário e dá menos voltas que o carretel R.
c) horário e dá mais voltas que o carretel R.
d) horário e dá menos voltas que o carretel R.
e) horário e dá o mesmo número de voltas que o carretel R.
7. (Uerj 2015) Em uma área onde ocorreu uma catástrofe natural, um helicóptero em
movimento retilíneo, a uma altura fixa do chão, deixa cair pacotes contendo alimentos. Cada
pacote lançado atinge o solo em um ponto exatamente embaixo do helicóptero.
Desprezando forças de atrito e de resistência, pode-se afirmar que as grandezas velocidade e
aceleração dessa aeronave são classificadas, respectivamente, como:
a) variável − nula
b) nula − constante
c) constante − nula
d) variável − variável
www.nsaulasparticulares.com.br
Página 3 de 68
8. (Espcex (Aman) 2015) No interior de um recipiente vazio, é colocado um cubo de material
homogêneo de aresta igual a 0,40 m e massa M  40 kg. O cubo está preso a uma mola ideal,
de massa desprezível, fixada no teto de modo que ele fique suspenso no interior do recipiente,
conforme representado no desenho abaixo. A mola está presa ao cubo no centro de uma de
suas faces e o peso do cubo provoca uma deformação de 5 cm na mola. Em seguida, colocase água no recipiente até que o cubo fique em equilíbrio com metade de seu volume submerso.
Sabendo que a densidade da água é de 1000 kg / m3 , a deformação da mola nesta nova
situação é de
Dado: intensidade da aceleração da gravidade g  10 m / s2
a) 3,0 cm
b) 2,5 cm
c) 2,0 cm
d) 1,5 cm
e) 1,0 cm
9. (Espcex (Aman) 2015) Uma pessoa de massa igual a 80 kg está dentro de um elevador
sobre uma balança calibrada que indica o peso em newtons, conforme desenho abaixo.
Quando o elevador está acelerado para cima com uma aceleração constante de intensidade
a  2,0 m / s2, a pessoa observa que a balança indica o valor de
Dado: intensidade da aceleração da gravidade g  10 m / s2
a) 160 N
b) 640 N
c) 800 N
d) 960 N
e) 1600 N
www.nsaulasparticulares.com.br
Página 4 de 68
10. (G1 - cps 2015) Manuel Bandeira dá ritmo e musicalidade ao seu poema Trem de Ferro,
imitando os sons produzidos por um trem.
Café com pão
Café com pão
Café com pão
Virge Maria que foi isso maquinista?
Agora sim
Café com pão
Agora sim
Voa, fumaça
Corre, cerca
Ai seu foguista
Bota fogo
Na fornalha
Que eu preciso
Muita força
Muita força
Muita força
(trem de ferro, trem de ferro)
Oô...
Foge, bicho
Foge, povo
Passa ponte
Passa poste
Passa pasto
Passa boi
Passa boiada
Passa galho
Da ingazeira
Debruçada
No riacho
Que vontade
De cantar!
(...)
(http://tinyurl.com/k78cyrf Acesso em: 31.07.2014.)
No poema, o referencial escolhido por Manuel Bandeira, de acordo com a Física Clássica, não
é ideal, pois interpretamos forças (falsas) em alguns objetos que de fato não a sofrem.
Suponha que a estrada de ferro é retilínea e que a força que move o trem refere-se a uma
força resultante e diferente de zero.
Tendo como referencial o foguista, sentado em sua cadeira na cabine da locomotiva, deve-se
interpretar o trem em ____________________ e o poste citado no verso “passa poste” em
____________________.
As expressões que completam corretamente a frase anterior, na ordem em que aparecem, são
a) repouso ... movimento com velocidade variável.
b) repouso ... movimento com velocidade constante.
c) movimento com velocidade variável ... repouso.
d) movimento com velocidade constante ... repouso.
e) movimento com velocidade variável ... movimento com velocidade variável.
www.nsaulasparticulares.com.br
Página 5 de 68
11. (Uel 2015) Considere que uma prensa aplica sobre uma chapa metálica uma força de
1,0  106 N, com o intuito de gravar e cortar 100 moedas.
Supondo que cada moeda possui raio igual a 1cm, assinale a alternativa que apresenta,
corretamente, a pressão total da prensa sobre a área de aplicação na chapa.
a)
104
Pa
π
b)
106
Pa
π
c)
108
Pa
π
d)
1010
Pa
π
e)
1012
Pa
π
12. (Ueg 2015) A pressão atmosférica no nível do mar vale 1,0 atm. Se uma pessoa que
estiver nesse nível mergulhar 1,5 m em uma piscina estará submetida a um aumento de
pressão da ordem de
a) 25%
b) 20%
c) 15%
d) 10%
13. (G1 - cftmg 2015) A imagem abaixo representa um bebedouro composto por uma base
que contém uma torneira e acima um garrafão com água e ar.
A pressão exercida pela água sobre a torneira, quando ela está fechada, depende diretamente
da(o)
a) diâmetro do cano da torneira.
b) massa de água contida no garrafão.
c) altura de água em relação à torneira.
d) volume de água contido no garrafão.
14. (Uerj 2015) Considere um corpo sólido de volume V . Ao flutuar em água, o volume de sua
parte submersa é igual a
V
V
; quando colocado em óleo, esse volume passa a valer .
8
6
Com base nessas informações, conclui-se que a razão entre a densidade do óleo e a da água
corresponde a:
a) 0,15
b) 0,35
c) 0,55
d) 0,75
www.nsaulasparticulares.com.br
Página 6 de 68
15. (Espcex (Aman) 2015) O desenho abaixo representa um sistema composto por cordas e
polias ideais de mesmo diâmetro. O sistema sustenta um bloco com peso de intensidade P e
uma barra rígida AB de material homogêneo de comprimento L. A barra AB tem peso
desprezível e está fixada a uma parede por meio de uma articulação em A . Em um ponto X
da barra é aplicada uma força de intensidade F e na sua extremidade B está presa uma corda
do sistema polias-cordas. Desprezando as forças de atrito, o valor da distância AX para que a
força F mantenha a barra AB em equilíbrio na posição horizontal é
a)
b)
c)
d)
e)
P L
8 F
P L
6 F
P L
4 F
P L
3 F
P L
2 F
16. (Ufrgs 2015) A elipse, na figura abaixo, representa a órbita de um planeta em torno de uma
estrela S. Os pontos ao longo da elipse representam posições sucessivas do planeta,
separadas por intervalos de tempo iguais. As regiões alternadamente coloridas representam as
áreas varridas pelo ralo da trajetória nesses intervalos de tempo. Na figura, em que as
dimensões dos astros e o tamanho da órbita não estão em escala, o segmento de reta SH
representa o raio focal do ponto H, de comprimento p.
Considerando que a única força atuante no sistema estrela-planeta seja a força gravitacional,
são feitas as seguintes afirmações.
I. As áreas S1 e S2 , varridas pelo raio da trajetória, são iguais.
II. O período da órbita é proporcional a P3 .
III. As velocidades tangenciais do planeta nos pontos A e H, VA e VH , são tais que VA  VH .
Quais estão corretas?
a) Apenas I.
b) Apenas I e II.
c) Apenas I e III.
d) Apenas II e III.
e) I, II e III.
www.nsaulasparticulares.com.br
Página 7 de 68
17. (Fuvest 2015) A notícia “Satélite brasileiro cai na Terra após lançamento falhar”, veiculada
pelo jornal O Estado de S. Paulo de 10/12/2013, relata que o satélite CBERS-3, desenvolvido
em parceria entre Brasil e China, foi lançado no espaço a uma altitude de 720 km (menor do
que a planejada) e com uma velocidade abaixo da necessária para colocá-lo em órbita em
torno da Terra. Para que o satélite pudesse ser colocado em órbita circular na altitude de
720 km, o módulo de sua velocidade (com direção tangente à órbita) deveria ser de,
aproximadamente,
Note e adote:
- raio da Terra  6  103 km
- massa da Terra  6  1024 kg

- constante da gravitação universal G  6,7  1011 m3 / s2kg

a) 61km / s
b) 25 km / s
c) 11km / s
d) 7,7 km / s
e) 3,3 km / s
18. (Ueg 2015) Uma carga Q está fixa no espaço, a uma distância d dela existe um ponto P,
no qual é colocada uma carga de prova q0 . Considerando-se esses dados, verifica-se que no
ponto P
a) o potencial elétrico devido a Q diminui com inverso de d.
b) a força elétrica tem direção radial e aproximando de Q.
c) o campo elétrico depende apenas do módulo da carga Q.
d) a energia potencial elétrica das cargas depende com o inverso de d2 .
19. (Unicamp 2015) Quando as fontes de tensão contínua que alimentam os aparelhos
elétricos e eletrônicos são desligadas, elas levam normalmente certo tempo para atingir a
tensão de U  0 V. Um estudante interessado em estudar tal fenômeno usa um amperímetro e
um relógio para acompanhar o decréscimo da corrente que circula pelo circuito a seguir em
função do tempo, após a fonte ser desligada em t  0 s. Usando os valores de corrente e
tempo medidos pelo estudante, pode-se dizer que a diferença de potencial sobre o resistor
R  0,5 kΩ para t  400 ms é igual a
a) 6 V.
b) 12 V.
c) 20 V.
d) 40 V.
www.nsaulasparticulares.com.br
Página 8 de 68
20. (Pucpr 2015) Para fazer o aquecimento
de uma sala durante o inverno, uma família
utiliza um aquecedor elétrico ligado à rede de
120 V. A resistência elétrica de operação
apresentada por esse aquecedor é de
14,4 Ω. Se essa família utilizar o aquecedor
diariamente, por três horas, qual será o custo
mensal cobrado pela companhia de energia
se a tarifa for de R$ 0,25 por kW  h?
Considere o mês de 30 dias.
a) R$ 15,00.
b) R$ 22,50.
c) R$ 18,30.
d) R$ 52,40.
e) R$ 62,80.
21. (Unicamp 2015) A figura 1
apresentada a seguir representa a
potência elétrica dissipada pelo
filamento de tungstênio de uma
lâmpada incandescente em função
da sua resistência elétrica. Já a
figura 2 apresenta a temperatura de
operação do filamento em função de
sua resistência elétrica. Se uma
lâmpada em funcionamento dissipa
150 W de potência elétrica, a
temperatura do filamento da
lâmpada é mais próxima de:
a) 325 C.
b) 1.250 C.
c) 3.000 C.
d) 3.750 C.
www.nsaulasparticulares.com.br
Página 9 de 68
22. (Ufsm 2015) Uma vez que a produção de energia elétrica, em qualquer de suas
modalidades, tem impactos ambientais, inovações que levem à diminuição do consumo de
energia são necessárias. Assim, as antigas lâmpadas incandescentes vêm sendo substituídas
por alternativas energeticamente mais eficientes. Naquele tipo de lâmpada, a emissão de luz
ocorre quando a temperatura de um filamento de tungstênio é elevada a valores entre 2.700 e
3.300K. Esse aquecimento ocorre como resultado da dissipação da energia dos elétrons ao
serem transportados através do condutor. Aquecimento e emissão de radiação infravermelha
consomem cerca de 90% da energia elétrica fornecida para a lâmpada. Com base nesse
conhecimento, considere a situação representada na tira a seguir.
Por que uma lâmpada incandescente de 100 W a 110 V, como a usada pelo personagem da
tira, queima quando ligada em uma rede de 220 V ?
a) Ao dobrar a tensão, a lâmpada dissipa energia a uma taxa quatro vezes maior.
b) Ao dobrar a tensão, a lâmpada dissipa energia a uma taxa duas vezes maior.
c) Ao dobrar a corrente, a lâmpada dissipa energia a uma taxa duas vezes maior.
d) Ao dobrar a corrente, a resistência da lâmpada cai à metade.
e) Ao dobrar a corrente, a potência da lâmpada cai à metade.
23. (Ufsm 2015) Em uma instalação elétrica doméstica, as tomadas são ligadas em
__________________ para que a mesma _________________________ em todos os
eletrodomésticos ligados a essa instalação.
Assinale a alternativa que completa as lacunas, na ordem.
a) paralelo ‒ tensão seja aplicada
b) paralelo ‒ corrente circule
c) paralelo ‒ potência atue
d) série ‒ tensão seja aplicada
e) série ‒ corrente circule
24. (Fuvest 2015) Dispõe se de várias
lâmpadas incandescentes de diferentes
potências, projetadas para serem utilizadas
em 110 V de tensão. Elas foram
acopladas, como nas figuras I, II e III
abaixo, e ligadas em 220 V.
Em quais desses circuitos, as lâmpadas
funcionarão como se estivessem
individualmente ligadas a uma fonte de
tensão de 110 V ?
a) Somente em I.
b) Somente em II.
c) Somente em III.
d) Em I e III.
e) Em II e III.
www.nsaulasparticulares.com.br
Página 10 de 68
25. (Uemg 2015) Em “Você Verá”, Luiz Vilela valoriza os animais. Por exemplo, no conto
“Quando fiz sete anos”, ele se lembra de uma bússola estragada, e de como voou “como um
alegre pássaro da manhã”, ao ir para casa, doido para abrir o embrulho onde estava uma
bússola estragada, que ganhara do avô.
Mas, por que a bússola estava estragada? Alguns candidatos aos cursos da UEMG fizeram
algumas hipóteses para responder a essa pergunta:
Leonardo: um fio solto fez com que o contato elétrico da bússola estragasse e, por isso, a
bússola deixou de funcionar.
Lorena: o Polo Norte da agulha da bússola apontava para o Polo Norte geográfico, e isto
estava errado, pois ele deveria apontar para o Polo Sul geográfico, pois um Polo Norte é
atraído por um Polo Sul.
Amanda: a agulha magnética poderia ter se desprendido de seu apoio, e não estava girando
livremente para se orientar, segundo o campo magnético da Terra.
Fez (fizeram) comentários apropriados
a) apenas Lorena.
b) Leonardo e Lorena.
c) apenas Amanda.
d) Leonardo e Amanda.
TEXTO PARA A PRÓXIMA QUESTÃO:
Recentemente, uma equipe de astrônomos afirmou ter identificado uma estrela com dimensões
comparáveis às da Terra, composta predominantemente de diamante. Por ser muito frio, o
astro, possivelmente uma estrela anã branca, teria tido o carbono de sua composição
cristalizado em forma de um diamante praticamente do tamanho da Terra.
26. (Unicamp 2015) Considerando que a massa e as dimensões dessa estrela são
comparáveis às da Terra, espera-se que a aceleração da gravidade que atua em corpos
próximos à superfície de ambos os astros seja constante e de valor não muito diferente.
Suponha que um corpo abandonado, a partir do repouso, de uma altura h  54 m da superfície
da estrela, apresente um tempo de queda t  3,0 s. Desta forma, pode-se afirmar que a
aceleração da gravidade na estrela é de
a) 8,0 m / s2 .
b) 10 m / s2 .
c) 12 m / s2 .
d) 18 m / s2 .
27. (Unicamp 2014) As máquinas cortadeiras
e colheitadeiras de cana-de-açúcar podem
substituir dezenas de trabalhadores rurais, o
que pode alterar de forma significativa a
relação de trabalho nas lavouras de cana-deaçúcar. A pá cortadeira da máquina ilustrada
na figura abaixo gira em movimento circular
uniforme a uma frequência de 300 rpm. A
velocidade de um ponto extremo P da pá vale
(Considere π  3. )
a) 9 m/s.
b) 15 m/s.
c) 18 m/s.
d) 60 m/s.
www.nsaulasparticulares.com.br
Página 11 de 68
28. (Uel 2014) Analise a figura a seguir.
Os habitantes de metrópoles convivem com o problema dos congestionamentos de
automóveis, que geram estresse, acidentes, poluição sonora, entre outras consequências. Uma
solução para o problema de mobilidade urbana é o transporte coletivo por linhas de metrô. A
figura mostra a região central da cidade de Brasília. Considere que um indivíduo se desloca
diariamente de carro da posição A, onde mora, até a posição B, onde trabalha, em um percurso
de 12 km representado pela linha tracejada. No horário de rush, a velocidade média dos
automóveis é de 12 km/h e, fora desse horário, é de 42 km/h. Se houvesse em Brasília uma
linha de metrô de A até B, como representado pela linha ponto-tracejada, ela teria 20 km.
Supondo que a velocidade média do metrô seja de 60 km/h, considere as afirmativas a seguir.
I. No horário de rush, o tempo de deslocamento de carro de A até B é maior do que o tempo de
deslocamento por metrô em 1 hora.
II. No horário de rush, o tempo de deslocamento de A até B por metrô é 1/3 do tempo de
deslocamento por carro.
III. Fora do horário de rush, é mais rápido fazer o percurso de A para B de carro.
IV. Fora do horário de rush, considerando que o sistema de metrô tenha melhorado e que sua
velocidade média passe a ser de 70 km/h, então o tempo de deslocamento de A até B tanto
por carro quanto por metrô é igual.
Assinale a alternativa correta.
a) Somente as afirmativas I e II são corretas.
b) Somente as afirmativas I e IV são corretas.
c) Somente as afirmativas III e IV são corretas.
d) Somente as afirmativas I, II e III são corretas.
e) Somente as afirmativas II, III e IV são corretas.
29. (Ufpr 2014) Considere um edifício em construção, constituído pelo andar térreo e mais dez
andares. Um servente de pedreiro deixou cair um martelo cuja massa é 0,5 kg a partir de uma
altura do piso do décimo andar. Suponha que cada andar tem uma altura de 2,5 m e que o
martelo caiu verticalmente em queda livre partindo do repouso. Considere a aceleração da
gravidade igual a 10 m/s2 e o martelo como uma partícula. Despreze a resistência do ar, a ação
do vento e a espessura de cada piso.
Levando em conta as informações dadas, analise as seguintes afirmativas:
1. A velocidade do martelo ao passar pelo teto do 1° andar era 20 m/s.
2. A energia cinética do martelo ao passar pelo piso do 5° andar era maior que 100 J.
3. Se a massa do martelo fosse o dobro, o tempo de queda até o chão diminuiria pela metade.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente a afirmativa 2 é verdadeira.
c) Somente as afirmativas 1 e 2 são verdadeiras.
d) Somente as afirmativas 2 e 3 são verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras.
www.nsaulasparticulares.com.br
Página 12 de 68
30. (Enem 2014) Um professor utiliza essa história em quadrinhos para discutir com os
estudantes o movimento de satélites. Nesse sentido, pede a eles que analisem o movimento do
coelhinho, considerando o módulo da velocidade constante.
Desprezando a existência de forças dissipativas, o vetor aceleração tangencial do coelhinho,
no terceiro quadrinho, é
a) nulo.
b) paralelo à sua velocidade linear e no mesmo sentido.
c) paralelo à sua velocidade linear e no sentido oposto.
d) perpendicular à sua velocidade linear e dirigido para o centro da Terra.
e) perpendicular à sua velocidade linear e dirigido para fora da superfície da Terra.
www.nsaulasparticulares.com.br
Página 13 de 68
31. (Espcex (Aman) 2014) Uma esfera é lançada com velocidade horizontal constante de
módulo v=5 m/s da borda de uma mesa horizontal. Ela atinge o solo num ponto situado a 5 m
do pé da mesa conforme o desenho abaixo.
Desprezando a resistência do ar, o módulo da velocidade com que a esfera atinge o solo é de:
Dado: Aceleração da gravidade: g=10 m/s2
a) 4 m / s
b) 5 m / s
c) 5 2 m / s
d) 6 2 m / s
e) 5 5 m / s
32. (Unifor 2014) A figura a seguir mostra uma das cenas vistas durante a Copa das
Confederações no Brasil. Os policiais militares responderam às ações dos manifestantes com
bombas de gás lacrimogêneo e balas de borracha em uma região totalmente plana onde era
possível avistar a todos.
Suponha que o projétil disparado pela arma do PM tenha uma velocidade inicial de
200,00 m / s ao sair da arma e sob um ângulo de 30,00º com a horizontal. Calcule a altura
máxima do projétil em relação ao solo, sabendo-se que ao deixar o cano da arma o projétil
estava a 1,70 m do solo.
Despreze as forças dissipativas e adote g  10,00 m / s2.
a) 401,70 m
b) 501,70 m
c) 601,70 m
d) 701,70 m
e) 801,70 m
www.nsaulasparticulares.com.br
Página 14 de 68
33. (Upf 2014) Durante uma experiência em um laboratório de física, um balão (desses usados
em festas de aniversário) cheio de ar, de massa total m = 1 g, carregado eletricamente com
uma carga q negativa, flutua estaticamente numa região do espaço onde existe um campo
elétrico uniforme na direção vertical e no sentido de cima para baixo. Desprezando-se o
empuxo sobre o balão e considerando que a aceleração gravitacional local é g = 10 m/s2 e que
o valor do campo elétrico é de 50 N/C, pode-se afirmar que a carga elétrica do balão é de:
a) 200 μC
b) 2 mC
c) 2  101 C
d) 5 mC
e) 5 μC
34. (Ufrgs 2014) Um plano inclinado com 5 m de comprimento é usado como rampa para
arrastar uma caixa de 120 kg para dentro de um caminhão, a uma altura de 1,5 m, como
representa a figura abaixo.
Considerando que a força de atrito cinético entre a caixa e a rampa seja de 564 N o trabalho
mínimo necessário para arrastar a caixa para dentro do caminhão é
a) 846 J.
b) 1056 J.
c) 1764 J.
d) 2820 J.
e) 4584 J.
35. (Upe 2014) A figura a seguir representa um ventilador fixado em um pequeno barco, em
águas calmas de um certo lago. A vela se encontra em uma posição fixa e todo vento soprado
pelo ventilador atinge a vela.
Nesse contexto e com base nas Leis de Newton, é CORRETO afirmar que o funcionamento do
ventilador
a) aumenta a velocidade do barco.
b) diminui a velocidade do barco.
c) provoca a parada do barco.
d) não altera o movimento do barco.
e) produz um movimento circular do barco.
www.nsaulasparticulares.com.br
Página 15 de 68
36. (G1 - ifce 2014) Na figura abaixo, o fio inextensível que une os corpos A e B e a polia têm
massas desprezíveis. As massas dos corpos são mA = 4,0 kg e mB = 6,0 kg. Desprezando-se
o atrito entre o corpo A e a superfície, a aceleração do conjunto, em m/s 2, é de (Considere a
aceleração da gravidade 10,0 m/s2)
a) 4,0.
b) 6,0.
c) 8,0.
d) 10,0.
e) 12,0.
37. (Cefet MG 2014) Uma caixa, inicialmente em repouso, sobre uma superfície horizontal e
plana, é puxada por um operário que aplica uma força variando linearmente com o tempo.
Sabendo-se que há atrito entre a caixa e a superfície, e que a rugosidade entre as áreas em
contato é sempre a mesma, a força de atrito, no decorrer do tempo, está corretamente
representada pelo gráfico
a)
b)
c)
d)
e)
www.nsaulasparticulares.com.br
Página 16 de 68
38. (Unifor 2014) Sobre um paralelepípedo de granito de massa m  900,0 kg, apoiado sobre
um terreno plano e horizontal, é aplicada uma força paralela ao plano de F  2.900,0 N. Os
coeficientes de atrito dinâmico e estático entre o bloco de granito e o terreno são 0,25 e 0,35,
respectivamente. Considere a aceleração da gravidade local igual a 10,0 m / s2 . Estando
inicialmente em repouso, a força de atrito que age no bloco é, em newtons:
a) 2.250
b) 2.900
c) 3.150
d) 7.550
e) 9.000
39. (Ufrgs 2014) Um móvel percorre uma trajetória fechada, representada na figura abaixo, no
sentido anti-horário.
Ao passar pela posição P, o móvel está freando. Assinale a alternativa que melhor indica,
nessa posição, a orientação do vetor aceleração total do móvel.
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
40. (Fuvest 2014) Uma estação espacial foi
projetada com formato cilíndrico, de raio R
igual a 100 m, como ilustra a figura abaixo.
Para simular o efeito gravitacional e permitir
que as pessoas caminhem na parte interna
da casca cilíndrica, a estação gira em torno
de seu eixo, com velocidade angular
constante ω. As pessoas terão sensação de
peso, como se estivessem na Terra, se a
velocidade ω for de, aproximadamente,
Note e adote:
A aceleração gravitacional na superfície da
Terra é g = 10 m/s2.
a) 0,1 rad/s
b) 0,3 rad/s
c) 1 rad/s
d) 3 rad/s
e) 10 rad/s
www.nsaulasparticulares.com.br
Página 17 de 68
41. (G1 - ifce 2014) Se cada quadrado, na figura abaixo, tem lado 1, é correto afirmar-se que
o vetor resultante mede
a) 20.
b) 20 2.
c) 5 2.
d) 10 2.
e) 10.
42. (Uerj 2014) A imagem abaixo ilustra uma bola de ferro após ser disparada por um canhão
antigo.
Desprezando-se a resistência do ar, o esquema que melhor representa as forças que atuam
sobre a bola de ferro é:
a)
b)
c)
d)
www.nsaulasparticulares.com.br
Página 18 de 68
43. (Upf 2014) A respeito do comportamento de um bloco apoiado sobre um plano inclinado,
analise as afirmativas a seguir e assinale a incorreta.
a) À medida que a inclinação do plano com a horizontal cresce, a componente da força peso
paralela ao plano também cresce.
b) Quando a inclinação do plano com a horizontal for de 30°, a componente da força peso
paralela ao plano terá um valor igual ao valor da metade do peso do bloco.
c) Para que a componente da força peso paralela ao plano tenha o mesmo valor que a
componente perpendicular ao plano, é preciso que a inclinação do plano seja de 45°.
d) Para um ângulo de 60° de inclinação, a componente da força peso paralela ao plano será de
3 do peso do bloco.
e) O peso do bloco será sempre o mesmo, independentemente do ângulo de inclinação do
plano.
44. (G1 - col.naval 2014) No dia 15 de abril, desse ano, ocorreu o eclipse lunar total. Nesse
fenômeno, a sombra da Terra é projetada sobre a Lua, encobrindo-a por completo. Entretanto,
uma parte da luz solar, que atravessou a atmosfera terrestre, refletiu-se na Lua com uma cor
avermelhada, produzindo o que se chamou de “Lua de Sangue”.
Considerando tal fato e tal fenômeno, analise as afirmativas abaixo e, em seguida, assinale a
opção correta.
I. Na Lua, onde não há atmosfera, o calor pode se propagar, somente, por condução e
irradiação.
II. Uma onda sonora, por não haver resistência do ar, propaga-se mais rapidamente na Lua, do
que na Terra.
III. A cor avermelhada, refletida na Lua, ocorreu devido refração da luz solar, ao atravessar a
atmosfera da Terra.
IV. A luz solar, sendo uma onda eletromagnética, propaga-se na Lua e na atmosfera terrestre
com a mesma velocidade.
V. Como a gravidade na Lua é cerca de 1 6 da gravidade na Terra, uma pessoa de 60 kg de
massa terá, na Lua, um peso de 100 N, considerando gTerra  10 m / s2.
a) Apenas as afirmativas II, IV e V são verdadeiras.
b) Apenas as afirmativas I, III e V são verdadeiras.
c) Apenas as afirmativas I, IV e V são verdadeiras.
d) Apenas as afirmativas II, III e IV são verdadeiras.
e) Apenas as afirmativas I, II e III são verdadeiras.
45. (Acafe 2014) Em um trabalho artístico impressionista, um escultor, utilizando um material
homogêneo de massa 1,0kg, constrói um cubo maciço de lado L. Para uma exposição é
requisitado que ele construa um cubo com o mesmo material em uma escala maior, onde o
lado desse novo cubo seja 2 L.
A alternativa correta que apresenta a massa, em kg, desse novo cubo é:
a) 3,0
b) 2,0
c) 4,0
d) 8,0
46. (Udesc 2014) Considere as proposições relacionadas aos fluidos hidrostáticos.
I. A pressão diminui com a altitude acima do nível do mar e aumenta com a profundidade
abaixo da interface ar-água.
II. O elevador hidráulico é baseado no Princípio de Pascal.
III. Sabendo-se que a densidade do gelo, do óleo e da água são iguais a
0,92 g / cm3 ; 0,80 g / cm3 e 1,0 g / cm3, respectivamente, pode-se afirmar que o gelo afunda
no óleo e flutua na água.
IV. O peso aparente de um corpo completamente imerso é menor que o peso real, devido à
ação da força de empuxo, exercida pelo líquido sobre o corpo, de cima para baixo.
Assinale a alternativa correta.
www.nsaulasparticulares.com.br
Página 19 de 68
a) Somente as afirmativas I, II e III são verdadeiras.
b) Somente as afirmativas II e IV são verdadeiras.
c) Somente as afirmativas I e II são verdadeiras.
d) Somente as afirmativas I, III e IV são verdadeiras.
e) Todas as afirmativas são verdadeiras.
47. (FMP 2014) Uma prensa hidráulica é composta por dois reservatórios: um cilíndrico e outro
em forma de prisma com base quadrada. O diâmetro do êmbolo do reservatório cilíndrico tem a
mesma medida que o lado do êmbolo do reservatório prismático. Esses êmbolos são
extremamente leves e podem deslocar-se para cima ou para baixo, sem atrito, e perfeitamente
ajustados às paredes dos reservatórios.
Sobre o êmbolo cilíndrico está um corpo de peso P.
A força que deve ser aplicada no êmbolo quadrado para elevar esse corpo deve ter intensidade
mínima igual a
P
a)
π
2P
b)
π
4P
c)
π
π P
d)
2
π P
e)
4
48. (Upf 2014) Uma barra metálica homogênea, de 2,0 m de comprimento e 10 N de peso,
está presa por um cabo resistente. A barra mantém dois blocos em equilíbrio, conforme mostra
a figura abaixo. Sendo d  0,5 m e o peso do bloco A, PA  100 N, é correto afirmar que o
peso do bloco B, em N, é:
a) 45
b) 30
c) 60
d) 6
e) 55
www.nsaulasparticulares.com.br
Página 20 de 68
49. (Ufrgs 2014) Na figura abaixo, blocos idênticos estão suspensos por cordas idênticas em
três situações distintas, (1), (2) e (3).
Assinale a alternativa que apresenta as situações na ordem crescente de probabilidade de
rompimento das cordas. (O sinal de igualdade abaixo indica situações com a mesma
probabilidade de rompimento).
a) (3), (2), (1).
b) (3), (2) = (1).
c) (1), (2), (3).
d) (1) = (2), (3).
e) (1) = (2) = (3).
50. (G1 - cftmg 2014) Um corpo A fica eletrizado positivamente quando atritado em um corpo
B e, em seguida, são colocados em suportes isolantes. Quando as barras metálicas C e D
tocam, respectivamente, A e B, ocorre transferência de
a) elétrons de C para A e de B para D.
b) prótons de A para C e de D para B.
c) elétrons de C para A e prótons de D para B.
d) prótons de A para C e elétrons de B para D.
51. (G1 - col.naval 2014) Com relação aos conceitos de eletricidade e magnetismo, coloque V
(verdadeiro) ou F (falso) nas afirmativas abaixo e, em seguida, assinale a opção que apresenta
a sequência correta.
(
) Na eletrização por atrito, o corpo que perde elétrons passa a ter mais prótons do que
possuía anteriormente e, nesse caso, fica eletrizado com carga positiva.
( ) Condutores são corpos que facilitam a passagem da corrente elétrica, pois possuem uma
grande quantidade de elétrons livres.
( ) Um ímã em forma de barra, ao ser cortado ao meio, dá origem a dois novos ímãs, cada
um com apenas um polo (norte ou sul).
( ) A bússola magnética, cuja extremidade encarnada é o seu polo norte, aponta para uma
direção definida da Terra, próxima ao Polo Norte Geográfico.
( ) Geradores são dispositivos que transformam outras formas de energia em energia
elétrica.
( ) O chuveiro elétrico pode ser considerado um resistor, pois transforma energia elétrica em
energia exclusivamente térmica.
a) F – V – F – V – V – V
b) F – F – V – V – F – V
c) V – F – F – V – V – F
d) V – V – V – F – F – F
e) F – V – V – F – F – V
www.nsaulasparticulares.com.br
Página 21 de 68
52. (Unicamp 2014) A atração e a repulsão entre partículas carregadas têm inúmeras
aplicações industriais, tal como a pintura eletrostática. As figuras abaixo mostram um mesmo
conjunto de partículas carregadas, nos vértices de um quadrado de lado a, que exercem forças
eletrostáticas sobre a carga A no centro desse quadrado. Na situação apresentada, o vetor que
melhor representa a força resultante agindo sobre a carga A se encontra na figura
a)
b)
c)
d)
53. (Ufrgs 2014) Na figura, estão representadas, no plano XY, linhas equipotenciais espaçadas
entre si de 1 V.
Considere as seguintes afirmações sobre essa situação.
I. O trabalho realizado pela força elétrica para mover uma carga elétrica de 1 C de D até A é de
1 J.
II. O módulo do campo elétrico em C é maior do que em B.
III. O módulo do campo elétrico em D é zero.
Quais estão corretas?
a) Apenas I.
b) Apenas II.
c) Apenas I e II.
d) Apenas II e III.
e) I, II e III.
54. (Ufrgs 2014) Observe o segmento de circuito.
No circuito, VA  20 V e VB  10 V são os potenciais nas extremidades A e B; e R1  2 kΩ,
R2  8 kΩ e R3  5 kΩ são os valores das resistências elétricas presentes. Nessa situação, os
potenciais nos pontos a e b são, respectivamente,
a) 24 V e 0 V.
b) 16 V e 0 V.
c) 4 V e 0 V.
d) 4 V e 5 V.
e) 24 V e 5 V.
www.nsaulasparticulares.com.br
Página 22 de 68
55. (G1 - col.naval 2014) Considere que um determinado estudante, utilizando resistores
disponíveis no laboratório de sua escola, montou os circuitos apresentados abaixo:
Querendo fazer algumas medidas elétricas, usou um voltímetro (V) para medir a tensão e um
amperímetro (A) para medir a intensidade da corrente elétrica. Considerando todos os
elementos envolvidos como sendo ideais, os valores medidos pelo voltímetro (situação 1) e
pelo amperímetro (situação 2) foram, respectivamente:
a) 2V e 1,2A
b) 4V e 1,2A
c) 2V e 2,4A
d) 4V e 2,4A
e) 6V e 1,2A
56. (Unesp 2014) Para compor a decoração de um ambiente, duas lâmpadas idênticas, L 1 e
L2, com valores nominais (100 V – 100 W), devem ser ligadas em paralelo a uma fonte de
tensão constante de 200 V. Deseja-se que L1 brilhe com uma potência de 100 W e que L 2
brilhe com uma potência de 64 W. Para que as lâmpadas não queimem, dois resistores
ôhmicos, R1 e R2, com valores convenientes, são ligados em série com as respectivas
lâmpadas, conforme o esquema representado na figura.
Considerando todos os fios utilizados na ligação como ideais e que as lâmpadas estejam
acesas e brilhando com as potências desejadas, é correto afirmar que os valores das
resistências de R1 e R2, em ohms, são, respectivamente, iguais a
a) 200 e 100.
b) 200 e 150.
c) 100 e 150.
d) 100 e 300.
e) 100 e 200.
57. (Udesc 2014) Assinale a alternativa incorreta a respeito de fenômenos eletromagnéticos.
a) Fios condutores paralelos e percorridos por correntes elétricas de mesmo sentido atraem-se,
enquanto os de sentidos opostos repelem-se.
b) Uma corrente elétrica é induzida em um circuito sempre que há uma variação do fluxo
magnético.
c) Um condutor percorrido por uma corrente elétrica, colocado em um campo magnético, sofre
a ação de uma força exercida por este campo.
d) Não é possível separar os polos magnéticos de um ímã permanente, em forma de barra,
quebrando-o.
e) Cargas elétricas em repouso ou em movimento produzem um campo elétrico e um campo
magnético.
www.nsaulasparticulares.com.br
Página 23 de 68
58. (Espcex (Aman) 2014) Dois fios “A” e “B” retos, paralelos e extensos, estão separados por
uma distância de 2 m. Uma espira circular de raio igual a π 4 m encontra-se com seu centro
“O” a uma distância de 2 m do fio “B”, conforme desenho abaixo.
A espira e os fios são coplanares e se encontram no vácuo. Os fios “A” e “B” e a espira são
percorridos por correntes elétricas de mesma intensidade i= 1 A com os sentidos
representados no desenho. A intensidade do vetor indução magnética resultante originado
pelas três correntes no centro “O” da espira é:
Dado: Permeabilidade magnética do vácuo: μ0  4π  107 T  m / A
a) 3,0  107 T
b) 4,5  107 T
c) 6,5  107 T
d) 7,5  107 T
e) 8,0  107 T
59. (Ufrgs 2014) Um trabalhador carregando uma esquadria metálica de resistência elétrica R
sobe, com velocidade de módulo constante, uma escada colocada abaixo de um fio
conduzindo uma corrente elétrica intensa, i. A situação está esquematizada na figura abaixo.
Assinale a alternativa correta sobre essa situação.
a) Como a esquadria tem, aos pares, lados paralelos, a força resultante exercida pelo fio acima
é nula.
b) Visto que o fio não atravessa a esquadria, a lei de Ampère afirma que não existem correntes
elétricas na esquadria.
c) À medida que sobe a escada, o trabalhador sente a esquadria “ficar mais leve”, resultado da
força atrativa exercida pelo fio, como previsto pela lei de Biot-Savart.
d) À medida que sobe a escada, o trabalhador sente a espira “ficar mais pesada”, resultado da
força de repulsão estabelecida entre a corrente elétrica no fio e a corrente elétrica induzida,
conforme explicado pela lei de Faraday-Lenz.
e) Como o trabalhador sobe com velocidade de módulo constante, não há o aparecimento de
corrente elétrica na esquadria.
www.nsaulasparticulares.com.br
Página 24 de 68
60. (Udesc 2014) Uma partícula, de massa m  5,0  1018 kg e carga q  8,0  106 C,
penetra perpendicularmente em um campo magnético uniforme, com velocidade constante de
módulo v  4,0  106 m / s, passando a descrever uma órbita circular de raio r  5,0  103 cm,
desprezando o efeito do campo gravitacional. O módulo do campo magnético a que a partícula
está submetida é igual a:
a) 4,0  104 T
b) 0,5  108 T
c) 2,0  106 T
d) 5,0  108 T
e) 5,0  107 T
61. (Uea 2014) Uma grandeza física que não possui unidade é chamada de adimensional. Um
exemplo desse tipo de grandeza física é
a) índice de refração.
b) tempo.
c) peso.
d) massa.
e) temperatura.
62. (G1 - ifsp 2014) A grandeza física energia pode ser representada de várias formas e com
a utilização de outras diferentes grandezas físicas. A composição destas outras grandezas
físicas nos define o que alguns chamam de formulação matemática.
Dentre elas, destacamos três:
E  mgh
E
K  x2
2
E
m  v2
2
Considerando o Sistema Internacional de Unidades, podemos representar energia como
a) kg  m  s1
b) kg  m2  s1
c) kg  m2  s2
d) kg  m2  s2
e) kg  m2  s2
63. (Ueg 2013) Alguns conceitos de física aparecem comumente no cotidiano e são
equivocadamente interpretados. Com relação a esse fato, o conceito correto é o seguinte:
a) calor é energia térmica em trânsito, enquanto temperatura caracteriza a energia térmica de
um sistema em equilíbrio.
b) energia é a medida de uma força atuando sobre um determinado corpo em movimento.
c) massa é a medida de inércia, enquanto peso é a intensidade da força gravitacional.
d) movimento e repouso são consequências da velocidade uniforme de um corpo material.
64. (Uerj 2013) Um bloco de madeira encontra-se em equilíbrio sobre um plano inclinado de
45º em relação ao solo. A intensidade da força que o bloco exerce perpendicularmente ao
plano inclinado é igual a 2,0 N. Entre o bloco e o plano inclinado, a intensidade da força de
atrito, em newtons, é igual a:
a) 0,7
b) 1,0
c) 1,4
d) 2,0
www.nsaulasparticulares.com.br
Página 25 de 68
65. (G1 - utfpr 2013) Em uma proveta que contém 100 cm3 de água, é colocada
cuidadosamente uma pepita de ouro com massa de 152 g. Observa-se que o nível da água
aumenta para 108 cm3. Qual a densidade da pepita?
a) 15,2 g/cm3.
b) 14 g/cm3.
c) 19 g/cm3.
d) 15,2 kg/m3.
e) 14 kg/m3.
66. (Epcar (Afa) 2013) Uma partícula de massa m e carga elétrica negativa gira em órbita
circular com velocidade escalar constante de módulo igual a v, próxima a uma carga elétrica
positiva fixa, conforme ilustra a figura abaixo.
Desprezando a interação gravitacional entre as partículas e adotando a energia potencial
elétrica nula quando elas estão infinitamente afastadas, é correto afirmar que a energia deste
sistema é igual a
1
a)  mv 2
2
1
b)  mv 2
2
2
mv 2
c) 
2
2
mv 2
d) 
2
67. (Upe 2013) Considere a Terra como uma esfera condutora, carregada uniformemente, cuja
carga total é 6,0 μC, e a distância entre o centro da Terra e um ponto P na superfície da Lua é
de aproximadamente 4 x 108 m. A constante eletrostática no vácuo é de aproximadamente 9 x
109 Nm2/C2. É CORRETO afirmar que a ordem de grandeza do potencial elétrico nesse ponto
P, na superfície da Lua vale, em volts,
a) 10-2
b) 10-3
c) 10-4
d) 10-5
e) 10-12
68. (Espcex (Aman) 2013) A pilha de uma lanterna possui uma força eletromotriz de 1,5 V e
resistência interna de 0,05 Ω. O valor da tensão elétrica nos polos dessa pilha quando ela
fornece uma corrente elétrica de 1,0 A a um resistor ôhmico é de
a) 1,45 V
b) 1,30 V
c) 1,25 V
d) 1,15 V
e) 1,00 V
www.nsaulasparticulares.com.br
Página 26 de 68
69. (Enem 2013) Um eletricista analisa o diagrama de uma instalação elétrica residencial para
planejar medições de tensão e corrente em uma cozinha. Nesse ambiente existem uma
geladeira (G), uma tomada (T) e uma lâmpada (L), conforme a figura. O eletricista deseja medir
a tensão elétrica aplicada à geladeira, a corrente total e a corrente na lâmpada. Para isso, ele
dispõe de um voltímetro (V) e dois amperímetros (A).
Para realizar essas medidas, o esquema da ligação desses instrumentos está representado
em:
a)
b)
c)
d)
e)
70. (Pucrj 2012) Um ciclista tentando bater um recorde de velocidade em uma bicicleta desce,
a partir do repouso, a distância de 1440 m em uma montanha cuja inclinação é de 30°. Calcule
a velocidade atingida pelo ciclista ao chegar à base da montanha.
2
Dados: Não há atrito e g = 10 m/s
a) 84 m/s
b) 120 m/s
c) 144 m/s
d) 157 m/s
e) 169 m/s
71. (G1 - ifpe 2012) O sistema da figura é formado por um bloco de 80 kg e duas molas de
massas desprezíveis associadas em paralelo, de mesma constante elástica. A força horizontal

F mantém o corpo em equilíbrio estático, a deformação elástica do sistema de molas é 20 cm
e a aceleração da gravidade local tem módulo 10 m/s2. Então, é correto afirmar que a
constante elástica de cada mola vale, em N/cm:
a) 10
b) 20
c) 40
d) 60
www.nsaulasparticulares.com.br
e) 80
Página 27 de 68
72. (Ifsul 2011) Uma caixa A, de peso igual a 300 N, é suspensa por duas cordas B e C
conforme a figura abaixo.
O valor da tração na corda B é igual a
a) 150,0 N.
b) 259,8 N.
c) 346,4 N.
d) 600,0 N.
73. (Uerj 2015) Admita uma colisão frontal totalmente inelástica entre um objeto que se move
com velocidade inicial v 0 e outro objeto inicialmente em repouso, ambos com mesma massa.
Nessa situação, a velocidade com a qual os dois objetos se movem após a colisão equivale a:
v
a) 0
2
v0
b)
4
c) 2v 0
d) 4v 0
74. (Ufrgs 2014) Um objeto de massa igual a 2 kg move-se em linha reta com velocidade
constante de 4 m / s. A partir de um certo instante, uma força de módulo igual a 2N é exercida
por 6 s sobre o objeto, na mesma direção de seu movimento. Em seguida, o objeto colide
frontalmente com um obstáculo e tem seu movimento invertido, afastando-se com velocidade
de 3 m / s.
O módulo do impulso exercido pelo obstáculo e a variação da energia cinética do objeto,
durante a colisão, foram, respectivamente,
a) 26 Ns e -91 J.
b) 14 Ns e -91 J.
c) 26 Ns e -7 J.
d) 14 Ns e -7 J.
e) 7 Ns e -7 J.
75. (Upf 2014) Em uma mesa de sinuca, uma bola é lançada frontalmente contra outra bola
em repouso. Após a colisão, a bola incidente para e a bola alvo (bola atingida) passa a se
mover na mesma direção do movimento da bola incidente. Supondo que as bolas tenham
massas idênticas, que o choque seja elástico e que a velocidade da bola incidente seja de 2
m/s, qual será, em m/s, a velocidade inicial da bola alvo após a colisão?
a) 0,5
b) 1
c) 2
d) 4
e) 8
www.nsaulasparticulares.com.br
Página 28 de 68
76. (Enem 2014) O pêndulo de Newton pode ser constituído por cinco pêndulos idênticos
suspensos em um mesmo suporte. Em um dado instante, as esferas de três pêndulos são
deslocadas para a esquerda e liberadas, deslocando-se para a direita e colidindo elasticamente
com as outras duas esferas, que inicialmente estavam paradas.
O movimento dos pêndulos após a primeira colisão está representado em:
a)
b)
c)
d)
e)
77. (Ufrgs 2015) Um bloco de massa 1kg move-se retilineamente com velocidade de módulo
constante igual a 3m / s, sobre urna superfície horizontal sem atrito. A partir de dado instante,
o bloco recebe o impulso de sua força externa aplicada na mesma direção e sentido de seu
movimento. A intensidade dessa força, em função do tempo, é dada pelo gráfico abaixo.
A partir desse gráfico, pode-se afirmar que o módulo da velocidade do bloco após o impulso
recebido é, em m / s, de
a)
b)
c)
d)
e)
6.
1.
5.
7.
9.
www.nsaulasparticulares.com.br
Página 29 de 68
78. (G1 - cftmg 2014) Um objeto, deslocando-se com uma quantidade de movimento de
20 kg  m / s, colide com um obstáculo durante 0,010 s e para. O valor médio da força impulsiva
que atua nesse objeto é, em newtons,
a) 1,0  101.
b) 2,0  101.
c) 1,0  103.
d) 2,0  103.
79. (Fuvest 2015) A figura abaixo mostra o gráfico da energia potencial gravitacional U de
uma esfera em uma pista, em função da componente horizontal x da posição da esfera na
pista.
A esfera é colocada em repouso na pista, na posição de abscissa x  x1, tendo energia
mecânica E  0. A partir dessa condição, sua energia cinética tem valor
Note e adote:
- desconsidere efeitos dissipativos.
a) máximo igual a U0 .
b) igual a E quando x  x3 .
c) mínimo quando x  x2 .
d) máximo quando x  x3 .
e) máximo quando x  x2 .
80. (Fuvest 2015) No desenvolvimento do sistema amortecedor de queda de um elevador de
massa m, o engenheiro projetista impõe que a mola deve se contrair de um valor máximo d,
quando o elevador cai, a partir do repouso, de uma altura h, como ilustrado na figura abaixo.
Para que a exigência do projetista seja satisfeita, a mola a ser empregada deve ter constante
elástica dada por
Note e adote:
- forças dissipativas devem ser ignoradas;
- a aceleração local da gravidade é g.
a) 2 m g h  d / d2
b) 2 m g h  d / d2
c) 2 m g h / d2
d) m g h / d
e) m g / d
www.nsaulasparticulares.com.br
Página 30 de 68
81. (G1 - ifce 2014) Paulo coloca a bola no gramado e bate um “tiro de meta”. A bola, após
descrever uma trajetória parabólica de altura máxima B, atinge o ponto C no gramado do
campo adversário.
Desprezando-se a resistência do ar e adotando-se o solo como referencial, é correto dizer-se
que
a) a energia da bola no ponto B é maior do que aquela que ela possui em qualquer outro ponto
de sua trajetória.
b) no ponto B, a bola possui energia cinética e energia gravitacional.
c) no ponto B, a energia cinética da bola é máxima, e a energia potencial é nula.
d) ao bater no gramado, no ponto C, toda a energia cinética da bola transforma-se em energia
potencial gravitacional.
e) a bola, no instante antes de colidir no gramado em C, já terá perdido toda a sua energia.
82. (Ifsc 2014) Frederico (massa 70 kg), um herói brasileiro, está de pé sobre o galho de uma
árvore a 5 m acima do chão, como pode ser visto na figura abaixo. Segura um cipó que está
preso em um outro galho, que permite-lhe oscilar, passando rente ao solo sem tocá-lo.
Frederico observa um pequeno macaco (massa 10 kg) no chão, que está preste a ser
devorado por uma onça, o maior felino da fauna brasileira. Desprezando a resistência do ar
para essa operação de salvamento, assinale a soma da(s) proposição(ões) CORRETA(S).
(considere Frederico e o macaco como partículas)
01) Há conservação de energia mecânica do nosso herói, quando ele oscila do galho da árvore
até o chão.
02) A velocidade do nosso herói, quando chega ao chão, antes de pegar o macaco, é 10 m/s.
04) O choque entre o nosso herói e o macaco é elástico.
08) O choque entre o nosso herói e o macaco é perfeitamente inelástico.
16) Imediatamente após pegar o macaco, a velocidade do conjunto (nosso herói e macaco) é
10 m/s.
32) Para esta operação de salvamento, houve conservação da quantidade de movimento.
www.nsaulasparticulares.com.br
Página 31 de 68
83. (Espcex (Aman) 2015) Uma das atrações mais frequentadas de um parque aquático é a
“piscina de ondas”. O desenho abaixo representa o perfil de uma onda que se propaga na
superfície da água da piscina em um dado instante.
Um rapaz observa, de fora da piscina, o movimento de seu amigo, que se encontra em uma
boia sobre a água e nota que, durante a passagem da onda, a boia oscila para cima e para
baixo e que, a cada 8 segundos, o amigo está sempre na posição mais elevada da onda.
O motor que impulsiona as águas da piscina gera ondas periódicas. Com base nessas
informações, e desconsiderando as forças dissipativas na piscina de ondas, é possível concluir
que a onda se propaga com uma velocidade de
a) 0,15 m / s
b) 0,30 m / s
c) 0,40 m / s
d) 0,50 m / s
e) 0,60 m / s
84. (Ufrgs 2015) Na figura abaixo, estão representadas duas ondas transversais P e Q, em
um dado instante de tempo.
Considere que as velocidades de propagação das ondas são iguais.
Sobre essa representação das ondas P e Q, são feitas as seguintes afirmações.
I. A onda P tem o dobro da amplitude da onda Q.
II. A onda P tem o dobro do comprimento de onda da onda Q.
III. A onda P tem o dobro de frequência da onda Q.
Quais estão corretas?
a) Apenas I.
b) Apenas II.
c) Apenas III.
d) Apenas I e II.
www.nsaulasparticulares.com.br
e) I, II e III.
Página 32 de 68
85. (Unicamp 2014) A tecnologia de telefonia celular 4G passou a ser utilizada no Brasil em
2013, como parte da iniciativa de melhoria geral dos serviços no Brasil, em preparação para a
Copa do Mundo de 2014. Algumas operadoras inauguraram serviços com ondas
eletromagnéticas na frequência de 40 MHz. Sendo a velocidade da luz no vácuo
c  3,0  108 m / s, o comprimento de onda dessas ondas eletromagnéticas é
a) 1,2 m.
b) 7,5 m.
c) 5,0 m.
d) 12,0 m.
86. (Fuvest 2014) O resultado do exame de audiometria de uma pessoa é mostrado nas
figuras abaixo. Os gráficos representam o nível de intensidade sonora mínima I, em decibéis
(dB), audível por suas orelhas direita e esquerda, em função da frequência f do som, em kHz. A
comparação desse resultado com o de exames anteriores mostrou que, com o passar dos
anos, ela teve perda auditiva. Com base nessas informações, foram feitas as seguintes
afirmações sobre a audição dessa pessoa:
I. Ela ouve sons de frequência de 6 kHz e intensidade de 20 dB com a orelha direita, mas não
com a esquerda.
II. Um sussurro de 15 dB e frequência de 0,25 kHz é ouvido por ambas as orelhas.
III. A diminuição de sua sensibilidade auditiva, com o passar do tempo, pode ser atribuída a
degenerações dos ossos martelo, bigorna e estribo, da orelha externa, onde ocorre a
conversão do som em impulsos elétricos.
É correto apenas o que se afirma em
a) I.
b) II.
c) III.
d) I e III.
e) II e III.
87. (Unicamp 2015) Espelhos
esféricos côncavos são
comumente utilizados por
dentistas porque, dependendo
da posição relativa entre objeto e
imagem, eles permitem
visualizar detalhes precisos dos
dentes do paciente. Na figura
abaixo, pode-se observar
esquematicamente a imagem
formada por um espelho
côncavo.
Fazendo uso de raios notáveis, podemos dizer que a flecha que representa o objeto
a) se encontra entre F e V e aponta na direção da imagem.
b) se encontra entre F e C e aponta na direção da imagem.
c) se encontra entre F e V e aponta na direção oposta à imagem.
d) se encontra entre F e C e aponta na direção oposta à imagem.
www.nsaulasparticulares.com.br
Página 33 de 68
88. (G1 - cftmg 2015) Analise o esquema abaixo referente a um espelho plano.
A imagem do objeto que será vista pelo observador localiza-se no ponto
a) 1
b) 2
c) 3
d) 4
89. (Ufg 2014) A figura a seguir representa um dispositivo óptico constituído por um laser, um
espelho fixo, um espelho giratório e um detector. A distância entre o laser e o detector é d = 1,0
m, entre o laser e o espelho fixo é h  3 m e entre os espelhos fixo e giratório é D = 2,0 m.
Sabendo-se que α  45, o valor do ângulo β para que o feixe de laser chegue ao detector é:
a) 15°
b) 30°
c) 45°
d) 60°
e) 75°
90. (Unesp 2014) Para observar uma
pequena folha em detalhes, um
estudante utiliza uma lente esférica
convergente funcionando como lupa.
Mantendo a lente na posição vertical
e parada a 3 cm da folha, ele vê uma
imagem virtual ampliada 2,5 vezes.
Considerando válidas as condições
de nitidez de Gauss, a distância focal,
em cm, da lente utilizada pelo
estudante é igual a
a) 5.
b) 2.
c) 6.
d) 4.
e) 3.
www.nsaulasparticulares.com.br
Página 34 de 68
91. (Ufrgs 2015) Na figura abaixo, um raio luminoso i, propagando-se no ar, incide radialmente
sobe placa semicircular de vidro.
Assinale a alternativa que melhor representa a trajetória dos raios r1 e r2 refratados,
respectivamente, no vidro e no ar.
a)
b)
d)
e)
c)
92. (FMP 2014)
A figura acima ilustra um raio monocromático que se propaga no ar e incide sobre uma lâmina
de faces paralelas, delgada e de espessura d com ângulo de incidência igual a 60. O raio
sofre refração, se propaga no interior da lâmina e, em seguida, volta a se propagar no ar.
Se o índice de refração do ar é 1, então o índice de refração do material da lâmina é
a)
6
3
6
2
2
c)
2
d) 6
e) 3
b)
www.nsaulasparticulares.com.br
Página 35 de 68
93. (G1 - cps 2015) Um dos materiais que a artista Gilda Prieto utiliza em suas esculturas é o
bronze. Esse material apresenta calor específico igual a 0,09 cal / (g  C), ou seja, necessita-se
de 0,09 caloria para se elevar em 1 grau Celsius a temperatura de 1 grama de bronze.
Se a escultura apresentada tem uma massa de bronze igual a 300 g, para que essa massa
aumente sua temperatura em 2C, deve absorver uma quantidade de calor, em calorias, igual
a
a) 6.
b) 18.
c) 27.
d) 36.
e) 54.
94. (Ueg 2015) A mudança do estado físico de determinada substância pode ser avaliada em
função da variação da temperatura em relação ao tempo, conforme o gráfico a seguir.
Considere que a 0C o composto encontra-se no estado sólido.
No gráfico, encontra-se a substância no estado líquido nos pontos
a) I, II e IV
b) III, IV e V
c) II, III e IV
d) I, III e V
95. (Unifor 2014) O café é uma das bebidas mais consumidas no mundo. O Brasil ainda é um
dos maiores exportadores desta rubiácea. Ao saborear uma xícara desta bebida em uma
cafeteria da cidade, André verificou que a xícara só estava morna. O café foi produzido a
100,00 C. A xícara era de porcelana cujo calor específico c x  0,26 cal / gC e sua
temperatura antes do contato com o café era de 25,00 C. Considerando o calor específico do
café de cc  1,0 cal / gC, a massa da xícara mx  50,00 g e a massa do café mc  150,00 g,
a temperatura aproximada da xícara detectada por André, supondo já atingido o equilíbrio
térmico e considerando não ter havido troca de calor com o ambiente, era:
a) 94,00 C
b) 84,00 C
c) 74,00 C
d) 64,00 C
e) 54,00 C
www.nsaulasparticulares.com.br
Página 36 de 68
96. (Ufg 2014) Uma longa ponte foi construída e instalada com blocos de concreto de 5 m de
comprimento a uma temperatura de 20°C em uma região na qual a temperatura varia ao longo
do ano entre 10°C e 40°C. O concreto destes blocos tem coeficiente de dilatação linear de 10 5
°C-1. Nessas condições, qual distância em cm deve ser resguardada entre os blocos na
instalação para que, no dia mais quente do verão, a separação entre eles seja de 1 cm?
a) 1,01
b) 1,10
c) 1,20
d) 2,00
e) 2,02
97. (Udesc 2014) Um sistema fechado, contendo um gás ideal, sofre um processo
termodinâmico isobárico, provocando mudança de temperatura de 200°C para 400°C. Assinale
a alternativa que representa a razão aproximada entre o volume final e o inicial do gás ideal.
a) 1,5
b) 0,5
c) 1,4
d) 2,0
e) 1,0
98. (Fuvest 2015) Certa quantidade de gás sofre três transformações sucessivas, A  B,
B  C e C  A, conforme o diagrama p  V apresentado na figura abaixo.
A respeito dessas transformações, afirmou-se o seguinte:
I. O trabalho total realizado no ciclo ABCA é nulo.
II. A energia interna do gás no estado C é maior que no estado A.
III. Durante a transformação A  B, o gás recebe calor e realiza trabalho.
Está correto o que se afirma em:
a) I.
b) II.
c) III.
d) I e II.
e) II e III.
99. (Fuvest 2015) O desenvolvimento de teorias científicas, geralmente, tem forte relação com
contextos políticos, econômicos, sociais e culturais mais amplos. A evolução dos conceitos
básicos da Termodinâmica ocorre, principalmente, no contexto
a) da Idade Média.
b) das grandes navegações.
c) da Revolução Industrial.
d) do período entre as duas grandes guerras mundiais.
e) da Segunda Guerra Mundial.
100. (Acafe 2014) Largamente utilizados na medicina, os termômetros clínicos de mercúrio
relacionam o comprimento da coluna de mercúrio com a temperatura. Sabendo-se que quando
a coluna de mercúrio atinge 2,0cm, a temperatura equivale a 34°C e, quando atinge 14cm, a
temperatura equivale a 46°C. Ao medir a temperatura de um paciente com esse termômetro, a
coluna de mercúrio atingiu 8,0cm.
A alternativa correta que apresenta a temperatura do paciente, em °C, nessa medição é:
a) 36
b) 42
c) 38
d) 40
www.nsaulasparticulares.com.br
Página 37 de 68
Gabarito:
Resposta da questão 1:
[C]
Em movimentos de sentidos opostos, o módulo da velocidade relativa é igual a soma dos
módulos das velocidades.
720
| vrel |  | v1 |  | v 2 |  360  360  720 km/h 
m/s 
3,6
| vr |  200 m/s.
Resposta da questão 2:
[B]
No gráfico v  t, a distância percorrida é obtida pela ”área" entre a linha do gráfico e o eixo dos
tempos. Calculando cada uma delas:

 2  0,5 1
2  0,5

 1 2  0,5  1,25  2  3,75 m.
DI 
2
2





1,5  1 2
1 1

 1,5  1  0,5  2,5  1,5  4,5 m.
DII 
2
2





2 1
 2  1  1  2  3 m.
DIII 
2





D  3  0,5   0,5  11  0,75  0,75  1,5 m.
IV
2
2

Resposta da questão 3:
[C]
Dados: f  24 Hz; Δt  3 min  180 s;  30 mm  0,03 m.
L  f Δ t  24  180  0,03  129,6 m 
L  130 m.
Resposta da questão 4:
[B]
A velocidade da correnteza é perpendicular ao barco, não interferindo no tempo de travessia.
Esse tempo depende apenas da velocidade de avanço do barco que é de 2 m/s. Portanto,
nesse caso, o tempo de travessia é o mesmo do que seria sem correnteza.
L
50
Δt 

 Δt  25 s.
vb
2
www.nsaulasparticulares.com.br
Página 38 de 68
Resposta da questão 5:
[B]
Dados : v  540 km/h  150 m/s; Δt  2,5 min  150 s.
a
Δ v 150  0


Δt
150
a  1 m/s2 .
Resposta da questão 6:
[D]
A análise da situação permite concluir que o carretel F gira no mesmo sentido que o carretel R,
ou seja, horário. Como se trata de uma acoplamento tangencial, ambos têm mesma velocidade
linear, igual à velocidade linear da fita.
f
r
vF  vR  2 π fF r F  2 π fR rR  f F r F  fR rR  F  R .
f R rF
Essa expressão final mostra que a frequência de rotação é inversamente proporcional ao raio.
Como o carretel F tem maior raio ele gira com menor frequência, ou seja dá menos voltas que
o carretel R.
Resposta da questão 7:
[C]
Depois de lançado, a componente horizontal da velocidade vetorial do pacote não mais se
altera, pois não há forças aplicadas no pacote nessa direção. Ou seja, nessa direção o
movimento é retilíneo e uniforme. Se cada pacote lançado atinge o solo em um ponto
exatamente embaixo do helicóptero, então a aeronave também está em MRU, sendo, então,
constante a velocidade e nula e aceleração.
Resposta da questão 8:
[E]
Dados: M  40kg; a  0,4m; dag  1.000kg / m3; x0  5cm.
Calculando a constante elástica da mola.
m g 400
Felá  P  k x 0  m g  k 

 k  80 N/cm.
x0
5
Na nova situação, o volume imerso é igual à metade do volume do corpo. Assim, no equilíbrio,
a resultante das forças atuantes, peso, empuxo e força elástica é nula.
Felá  E  P  k x  dág Vim g  m g  80 x  103 
80 x  400  320  x 
80

80
 0,4 3
2
 10  400 
x  1 cm.
Resposta da questão 9:
[D]
Entendendo que a balança do enunciado seja na verdade um dinamômetro, a leitura indicada é
a intensidade (FN) da força normal que a plataforma do dinamômetro aplica nos pés da pessoa:
FN  P  m a  FN  800  80  2  
FN  960 N.
www.nsaulasparticulares.com.br
Página 39 de 68
Resposta da questão 10:
[A]
Como o referencial é o foguista, que está em repouso em relação ao trem, então o trem está
em repouso em relação ao foguista. Em relação ao solo, como a resultante das forças sobre o
trem é não nula, ele tem movimento acelerado. O poste está fixo no solo, logo para o
referencial foguista, o poste passa em movimento com velocidade variável.
Resposta da questão 11:
[C]
p
F
F
106
106




2
2
A 100 π r 2
2
10
π
100  π 1 10
p


108
Pa.
π
Resposta da questão 12:
[C]
Considerando a Lei de Stevin da Hidrostática, temos que a pressão manométrica submetida
pelo mergulhador depende da profundidade h , da massa específica do fluido μ e da
aceleração da gravidade g.
pm  μgh

pm  1000
kg
3
m
 10
m
s2
 1,5m

pm  15000Pa
1,0  105 Pa
 100000Pa
atm
p  pm  patm  15000  100000  115000Pa
patm  1,0atm 
Logo, a pressão total representa um aumento de 15% em relação à pressão atmosférica.
Resposta da questão 13:
[C]
De acordo com o Teorema de Stevin, a pressão exercida por uma coluna líquida é diretamente
proporcional à altura dessa coluna.
www.nsaulasparticulares.com.br
Página 40 de 68
Resposta da questão 14:
[D]
Se o corpo está parcialmente imerso, o empuxo e o peso estão equilibrados. Sendo m e V a
massa e o volume do corpo, respectivamente, Vi o volume imerso, dC a densidade do corpo e
dL a densidade do líquido, temos:
dC Vi
P  E  dC V g  dL Vi g 
 .
dL
V
Aplicando os dados da questão nessa expressão:
V
 d
dC
1
 C  8 

 dágua
V
dágua 8
dC Vi 
dC
d
1 6 6 3

 
 óleo    


dL
V 
dágua
dC
8 1 8 4
V
 d
dC
1

 C  6 
V
dóleo 6
 dóleo
dóleo
 0,75.
dágua
Resposta da questão 15:
[A]
Em cada polia móvel, se o peso é desprezível, a força é dividida por dois. Assim, a força
transmitida à extremidade da barra é 1/8 do peso do bloco, como indicado na figura.
Como a barra está em equilíbrio, o somatório dos momentos em relação à articulação A é nulo.
Então:
F  Ax 
P
L 
8
Ax 
P L
.
8 F
Resposta da questão 16:
[C]
[I] Correta. A segunda lei de Kepler afirma que o segmento de reta Sol-planeta varre áreas
iguais em intervalos de tempo iguais.
[II] Incorreta. O período da órbita é proporcional ao quadrado do raio médio da trajetória.
[III] Correta. O movimento do planeta é acelerado de H para A e retardado de A para H.
Portanto, VA  VH.
www.nsaulasparticulares.com.br
Página 41 de 68
Resposta da questão 17:
[D]
Dados:
R  6  103 km  6  106 m; h  720 km  0,72  106 m; M  6  1024 kg;
G  6,7  1011 m3 /kg  s2 .
Como a órbita é circular, a gravidade tem a função de aceleração centrípeta.
ac  g 
v
GM
GM
v2

 v

R  h  R  h 2
Rh
6,7  1011  6  1024
6,72  106
6,7  1011  6  1024
6  106  0,72  106

 60  106  7,7  103 m/s 
v  7,7 km/s.
Resposta da questão 18:
[A]
Com as expressões de força elétrica, campo elétrico, potencial elétrico e energia potencial
elétrica abaixo podemos tecer algumas considerações sobre as alternativas expostas.
O potencial elétrico de uma carga puntiforme é dado pelo produto do campo elétrico pela
Q
Q
distância à carga geradora V  E  d  k0
 d  V  k 0 . Sendo assim, temos a alternativa
2
d
d
[A] como correta.
A força elétrica, dada pela Lei de Coulomb Fe  k 0
Q  q0
tem a direção da reta que une os
d2
centros das duas cargas podendo ter o sentido de afastamento se as cargas forem de mesmo
sinal (repulsão) ou de aproximação (atração) se as cargas forem de sinais contrários.
Alternativa [B] incorreta.
F
Q
, logo não depende
O campo elétrico é a razão entre a força e a carga de prova E  e  k 0
q0
d2
apenas da carga Q e também da distância entre as cargas. Alternativa [C] incorreta.
A energia potencial elétrica é dada pelo produto do potencial elétrico e a carga de prova, então
Qq0
Q
Ep  q0  V  q0  k0  Ep  k0
. A alternativa [D] está incorreta, pois a dependência é
d
d
com o inverso de d.
Resposta da questão 19:
[A]
Dado: R  0,5 kΩ  0,5  103 Ω; i  12 mA  12  103 A.
Aplicando a 1ª Lei de Ohm:
U  R i  0,5  103  12  103 
U  6 V.
www.nsaulasparticulares.com.br
Página 42 de 68
Resposta da questão 20:
[B]
A Energia Elétrica é dada por: E  P  Δt, onde:
E  energia elétrica em joules (J) no Sistema Internacional (SI), porém para o problema é
conveniente usar a unidade usual kWh;
P  potência elétrica em watts no SI. Usaremos em kW;
Δt  tempo em segundos (s) no SI. Usaremos em horas (h).
Primeiramente, calculamos a Potência Elétrica com a equação: P  U  i, em que:
U  diferença de potencial elétrico em volts (V);
i  intensidade da corrente elétrica em ampères (A).
Como não dispomos do valor da intensidade da corrente elétrica (i), usamos a 1ª Lei de Ohm
para substituí-la por uma relação entre diferença de potencial e resistência.
U
U  Ri  i 
R
Substituindo na equação da potência, temos:
P
U2
, onde R  resistência elétrica em ohms (Ω)
R
Logo, P 
120 V 2
14,4 Ω

14400 V2
 1000 W  1 kW
14,4 Ω
A Energia Elétrica em kWh será: E  P  Δt  1 kW 
3h
 30dias  90 kWh
dia
Como o custo mensal da Energia Elétrica consumida é apenas o produto da Energia Elétrica
em kWh pelo seu valor, temos:
Custo  90kWh 
R$0,25
 R$22,50
kWh
www.nsaulasparticulares.com.br
Página 43 de 68
Resposta da questão 21:
[C]
Basta seguir a seta em cada um dos gráficos.
No gráfico da figura 1, para a potência de 150 W obtemos que a resistência é de 325Ω. No
gráfico da figura 2, para a resistência de 325Ω, obtemos a temperatura de 3.000C.
Resposta da questão 22:
[A]
A energia dissipada (E) num resistor de resistência R sujeito a uma tensão U é dada pela
expressão:
E
U2
Δt. Assim, ao dobrar a tensão, a energia dissipada fica quatro vezes maior
R
Resposta da questão 23:
[A]
As tomadas de uma residência devem ser ligadas em paralelo para que os aparelhos possam
funcionar independentemente e para que se possa aplicar a tensão adequada a cada
eletrodoméstico.
www.nsaulasparticulares.com.br
Página 44 de 68
Resposta da questão 24:
[D]
Considerações:
U2
. Com base nessa
R
expressão, se definirmos como R a resistência das lâmpadas de 120 W, as lâmpadas de 60
W e 40 W têm resistências iguais a 2 R e 3 R, respectivamente;
2ª) Na associação em série, lâmpadas de mesma resistência estão sob mesma tensão. Se as
resistências são diferentes, as tensões são divididas em proporção direta aos valores das
resistências.
3ª) Na associação em paralelo, a tensão é a mesma em todas as lâmpadas;
4ª) A tensão em cada lâmpada deve ser 110 V.
1ª) A expressão que relaciona tensão, potência e resistência é P 
As figuras abaixo mostram as simplificações de cada um dos arranjos, destacando as tensões
nas lâmpadas em cada um dos ramos.
Arranjo (I): todas as lâmpadas estão sob tensão de 110 V.
Arranjo (II): somente uma das lâmpadas está sob tensão de 110 V.
www.nsaulasparticulares.com.br
Página 45 de 68
Arranjo (III): todas as lâmpadas estão sob tensão de 110 V.
Resposta da questão 25:
[C]
Justificando os comentários inapropriados:
Leonardo: inapropriado – na bússola não há circuito elétrico algum.
Lorena: inapropriado – o Polo Norte da agulha deve mesmo apontar para o Polo Norte
geográfico, que corresponde ao Sul magnético. Só não entendemos porque, então, a bússola
estava estragada.
Amanda: apropriado.
Resposta da questão 26:
[C]
h
2 h 2  54
g 2
t  g


2
t2
32
g  12 m/s2 .
Resposta da questão 27:
[C]
Dados: f = 300 rpm = 5 Hz; π = 3; R = 60 cm = 0,6 m.
A velocidade linear do ponto P é:
v  ω R  2 f R  2  3  5  0,6 
v  18 m/s.
www.nsaulasparticulares.com.br
Página 46 de 68
Resposta da questão 28:
[E]
[I] Incorreta. No horário de rush, o tempo de deslocamento de carro de A até B é igual ao o
tempo de deslocamento por metrô em 1 hora.
ΔScarro 12
Δtcarro 

 Δtcarro  1 h.
vrush
12
[II] Correta.

ΔScarro 12

 Δtcarro  1 h
Δtcarro 
vrush
12


ΔSmetrô 20
1
Δt


 Δtmetrô 
h
 metrô
v
60
3
metrô

 Δtmetrô 
[III] Correta.

ΔScarro 12
2

 Δtcarro 
h  0,29 h
Δtcarro 
vrush
42
7


ΔSmetrô 20
1
Δt


 Δtcarro 
h  0,33 h
 metrô
v
60
3
metrô

[IV] Correta.

ΔScarro 12
2

 Δtcarro 
h
Δtcarro 
vrush
42
7


ΔSmetrô 20
2
Δt


 Δtcarro 
 metrô
v
70
7
metrô

1
Δtcarro .
3
 Δtcarro  Δtmetrô
 Δtcarro  Δtmetrô
Resposta da questão 29:
[A]
Dados: m = 0,5 kg; h = 2,5 m; g = 10 m/s2.
[1] Correta. Do piso do 10º andar até o teto do 1º andar há oito andares. Assim, aplicando
Torricelli:
v 2  v 02  2 g H
 v 2  2 10  8  2,5   v 2  400 
v  20 m/s.
[2] Incorreta. Do piso do 10º andar até o piso do 5º andar há cinco andares. Assim, aplicando a
conservação da Energia Mecânica:
f
i
EMec
 EMec

Ecin  m g ( 5 h )  0,5 10  5  2,5  
Ecin  62,5 J.
[3] Incorreta. O tempo de queda livre independe da massa.
Resposta da questão 30:
[A]
Como o módulo da velocidade é constante, o movimento do coelhinho é circular uniforme,
sendo nulo o módulo da componente tangencial da aceleração no terceiro quadrinho.
www.nsaulasparticulares.com.br
Página 47 de 68
Resposta da questão 31:
[E]
1ª Solução:
O tempo de queda da esfera é igual ao tempo para ela avançar 5 m com velocidade horizontal
constante de v0 = 5 m/s.
x
5
t
  1 s.
v0 5
A componente vertical da velocidade é:
v y  v0y  g t  v y  0  10 1  v y  10 m/s.
Compondo as velocidades horizontal e vertical no ponto de chegada:
v 2  v02  v 2y  v  52  102
 v  125 
v  5 5 m/s.
2ª Solução:
Calculando a altura de queda:
1
2
h  g t 2  h  5 1
 h  5 m.
2
Pela conservação da energia mecânica:
m v02
m v2
m g h
2
2
v  5 5 m/s.
 v  v 02  2 g h  v  52  2 10  5   125 
Resposta da questão 32:
[B]
Dados: θ  30; v0  200m / s; h0  1,7m; g  10m / s2.
1ª Solução:
Decompondo a velocidade inicial nas direções horizontal e vertical:

3
v  v 0 cos θ  200cos30  200
 v 0x  100 3 m/s.

 0x
2

v  v sen θ  200 sen 30  200 1  v  100 m/s.
0y
0
0x


2
Sabemos que no ponto mais alto a componente vertical da velocidade é nula (vy = 0).
Aplicando a equação de Torricelli nessa direção, vem:
10.000
2
v 2y  v oy
 2 g H  h0   0  1002  20 H  1,7   H  1,7 

20
H  500  1,7 
H  501,7 m.
www.nsaulasparticulares.com.br
Página 48 de 68
2ª Solução:
No ponto mais alto, a componente vertical da velocidade é nula, portanto v = vx = v0x.
Pela conservação da Energia Mecânica:
m v 02
m v 2x
 m g h0 
 m gH 
2
2
20.000  17  15.000  10 H  H 

100 3
2002
 10 1,7  
2
2
5.017
10

2
 10 H 

H  501,7 m.
Resposta da questão 33:
Sem resposta.
Gabarito Oficial: [A]
Gabarito SuperPro®: Sem resposta.
O próprio enunciado afirma que a carga do balão é negativa, mas não coloca o sinal (–) em
nenhuma das opções, que apresentam apenas o módulo dessa carga.
Se o balão está em equilíbrio, a intensidade da força elétrica é igual à do peso.
Fel  P 
q Emg 
q 
m g 101  10

 2  104 
E
50
q  200  10 6 C 
q  200 μC.
Resposta da questão 34:
[E]
Dados: m  120kg; ΔS  5m; h  1,5m; g  9,8m / s2; Fat  564N.
Considerando que as velocidades inicial e final sejam nulas, o trabalho é mínimo quando a
força na subida da rampa é aplicada paralelamente ao deslocamento. Aplicando o teorema da
energia cinética, temos:
WRe s  ΔEC  WF  WP  WFat  0  WF  m g h  Fat ΔS  0 
WF  m g h  Fat ΔS  WF  120  9,8  1,5  564  5  1.764  2.820 
WF  4.584 J.
Resposta da questão 35:
[D]
O ventilador sopra ar para frente, recebendo uma força de reação para trás; todo o vento
soprado atinge a vela, aplicando nela uma força para frente. Assim, agem no sistema barcovela-ventilador duas forças de mesma intensidade e de sentidos opostos, sendo nula a
resultante nesse sistema. Portanto, nenhuma alteração ocorre no movimento do barco.
Resposta da questão 36:
[B]
Aplicando o Princípio Fundamental da Dinâmica ao sistema:
PB  mA  mB  a  60  10 a  a  6 m/s2.
www.nsaulasparticulares.com.br
Página 49 de 68
Resposta da questão 37:
[B]
No início, a força de atrito (A) é estática e tem valor nulo. À medida que o operário aumenta a
intensidade da força aplicada, a intensidade da força de atrito estática também aumenta, até
atingir o valor máximo (Amáx  μeN), na iminência de escorregamento. Ultrapassado esse
valor, a caixa entra em movimento, a força de atrito passa a ser cinética, constante
(Acin  μcN), sendo Acin  Amáx , pois o coeficiente de atrito cinético é menor que o estático.
Resposta da questão 38:
[B]
Dados: m  900kg; F  2.900N; μC  0,25; μE  0,35; g  10m / s2.
Calculando a força de atrito estático máxima:
Fat máx  μE N  μE m g  0,35  900  10  Fat máx  3.150 N.
Como a força de atrito estático máxima tem maior intensidade que aplicada paralelamente ao
plano, o bloco não entra em movimento. Assim, a força resultante sobre ele é nula.
Então:
Fat  F 
Fat  2.900 N.
Resposta da questão 39:
[D]
O movimento é curvilíneo retardado. Portanto, a componente tangencial da aceleração  at 
tem sentido oposto ao da velocidade a componente centrípeta  ac  dirigida para o centro. A
figura ilustra a situação.
Resposta da questão 40:
[B]
A normal, que age como resultante centrípeta, no pé de uma pessoa tem a mesma intensidade
de seu peso na Terra.
N  Rcent  P  m ω2 R  m g  ω 
g
10
1


r
100
10

ω  0,3 rad/s.
www.nsaulasparticulares.com.br
Página 50 de 68
Resposta da questão 41:
[C]
Pela regra da poligonal, temos:
 
R2  52  52  2 52
 R5 2 .
Resposta da questão 42:
[A]
Após o lançamento, a única força que age sobre a bola é seu próprio peso, vertical e para
baixo.
Resposta da questão 43:
[D]
A figura mostra as componentes da força peso de um corpo que está sobre um plano inclinado:
Calculando a intensidade (Px ) da componente paralela ao plano:
sen 60 
Px
3
 Px  P sen 60  Px  P
.
P
2
www.nsaulasparticulares.com.br
Página 51 de 68
Resposta da questão 44:
[B]
[I] Verdadeira. Se não há atmosfera, é impossível haver convecção. Portanto a transferência de
calor de um corpo para outro só pode ocorrer por condução ou por irradiação.
[II] Falsa. O som é uma onda mecânica, necessitando de meio material para se propagar.
[III] Verdadeira.
[IV] Falsa. O índice de refração da atmosfera terrestre é maior que o do vácuo, portanto na
atmosfera terrestre a velocidade da luz solar é menor do que na Lua.
10
[V] Verdadeira. P  m g  60
 P  100 N.
6
Resposta da questão 45:
[D]
m  d V  m  d L3
1
1
 1

3
m 2  d V2  m 2  d  2 L 

m1
L3
L3


m 2  2 L 3
8 L3

1,0 1


m2 8
m2  8,0 kg.
Resposta da questão 46:
[A]
Justificando a falsa:
[I] Verdadeira.
[II] Verdadeira.
[III] Verdadeira.
[IV] Falsa. O peso aparente de um corpo completamente imerso é menor que o peso real,
devido à ação da força de empuxo, exercida pelo líquido sobre o corpo, de baixo para cima.
Resposta da questão 47:
[C]
A figura mostra as forças agindo sobre os êmbolos de áreas A1 e A2.
Aplicando o Teorema de Pascal:
F
P

A 2 A1

F
2
D

P
2
πD
4

F
4P
.
π
www.nsaulasparticulares.com.br
Página 52 de 68
Resposta da questão 48:
[B]
Dados: L = 2 m; P = 10 N; d = 0,5 m; PA = 100 N.
A figura mostra as dimensões relevantes para a resolução da questão.
Como a barra está em equilíbrio, em ralação ao ponto O, o somatório dos momentos em
sentido anti-horário é igual ao somatório dos momentos em sentido horário.
M PB  MP  M PA  PB 1,5   10  0,5   100  0,5   1,5 PA  45 
PA  30 N.
Resposta da questão 49:
[A]
Analisemos a figura abaixo que mostra as forças que atuam no bloco.
Na horizontal, as componentes da tração se equilibram. Na vertical, para haver equilíbrio:
P
2 Ty  P  2 T sen θ  P  T 
.
2 sen θ
Aplicando essa expressão em cada um dos casos:

P
P

 T1  P
T1 
1
2
sen
30


2
2


P
P
P
3

T

 T2 
P  T2  0,58 T

T2 
2 sen θ 
2 sen 60
3
3
2

2

P
P
T 

 T3  0,5 T
 3 2 sen 90 2
T3  T2  T1.
www.nsaulasparticulares.com.br
Página 53 de 68
Resposta da questão 50:
[A]
Durante a eletrização por atrito, os corpos adquirem cargas de mesmo módulo e de sinais
opostos. Portanto, se o corpo A fica eletrizado positivamente, o corpo B fica eletrizado
negativamente.
Como não foram dados os estados elétricos iniciais das barras metálicas, C e D, a questão fica
sem resposta.
Supondo que as barras metálicas estejam, inicialmente, eletricamente neutras, passarão
elétrons de C para A e de B para D.
Resposta da questão 51:
[A]
[F] A quantidade de prótons não varia.
[V] Os elétrons da camada mais externa são mais fracamente ligados aos núcleos, formando a
nuvem eletrônica. Esses são os elétrons livres que se deslocam formando a corrente
elétrica quando se aplica uma ddp aos terminais do condutor.
[F] Os polos de um ímã são inseparáveis. Os dois ímãs terão polos norte e sul.
[V] A Terra é um grande ímã, ficando o polo norte geográfico próximo ao polo sul magnético,
para onde aponta o polo norte da agulha da bússola.
[V] É a própria definição de gerador.
[V] Resistores transformam energia elétrica em térmica (efeito Joule). Convém ressaltar que no
caso das lâmpadas incandescentes, a temperatura fica muito elevada, sendo parte da energia
elétrica transformada em luminosa.
Resposta da questão 52:
[D]
A figura mostra as forças atrativas e repulsivas agindo sobre a carga A, bem como a resultante
dessas forças.
www.nsaulasparticulares.com.br
Página 54 de 68
Resposta da questão 53:
[C]
Gabarito Oficial: [B]
Gabarito SuperPro®: [C]
[I] Correta. O trabalho (W) da força elétrica para transportar uma carga de prova entre dois
pontos do campo elétrico e obtido pela aplicação do teorema da energia potencial.
W D,A   VD  VA  q   0  1  1  W D,A  1 J.
Fel
Fel
[II] Correta. Para uma mesma ddp entre duas superfícies equipotenciais, quanto mais intenso é
o vetor campo elétrico, mais próximas estão as superfícies. Na figura, à medida que se
desloca de C para B, a distância entre duas superfícies aumenta, indicando que a
intensidade do vetor campo elétrico está diminuindo, ou seja, EC > EB.
[III] Incorreta. Se o campo fosse nulo, não haveria diferença de potencial.
Resposta da questão 54:
[B]
Dados: VA  20 V; VB  10 V; R1  2 kΩ; R2  8 kΩ; R3  5 kΩ.
Como os resistores estão em série, a resistência equivalente entre A e B é:
Req  R1  R2  R3  2  8  5  Req  15 kΩ  15  103 Ω.
Como VB > VA, o sentido da corrente é de B para A e tem intensidade:
VB  VA  Req i  10   20   15  103 i  30  15  103 i 
i  2 103 A.
Entre a e A:
Va  VA  R1 i  Va   20   2  103  2  103  Va  4  20 
Va  16 V.
Entre b e a:
Vb  Va  R2 i  Vb   16   8  103  2  103  Vb  16  16 
Vb  0 V.
Resposta da questão 55:
[B]
Situação I
Como os resistores estão em série, a resistência equivalente é igual à soma das resistências.
O valor medido pelo voltímetro é a ddp no resistor de 40.
Aplicando a lei de Ohm-Pouillet:
12
ε  Re q i  12   60  40  20  i  i 
 i  0,1 A.
120
U  R i  40  0,1 
U  4 V.
www.nsaulasparticulares.com.br
Página 55 de 68
Situação II
Calculando a resistência equivalente:
1
1
1
1 1 2  3
6
1






Req 60 30 20
60
60 10
 Req  10 Ω.
O valor medido pelo amperímetro é a corrente total no circuito.
Aplicando a lei de Ohm-Pouillet:
ε
12
ε  Req i  i 

 i  1,2 A.
Req 10
Resposta da questão 56:
[C]
Na lâmpada 1:
P1  U1 i1  100  100 i1  i1  1 A.
U  U1  R1 i1  200  100  R1 1 
R1  100 Ω.
Na lâmpada 2, supondo que a resistência mantenha-se constante:

U2
P2  2

R

2
U'2

P'

 2
R
 
P2
U2
R
 2 2
P'2
R U'2
P'2  U'2 i2  64  80 i2

100  100 


64  U'2 
2

10 100

 U'2  80 V.
8
U'2
 i2  0,8 A.
U  U'2  R2 i2  200  80  R2  0,8   R2 
120
0,8

R2  150 Ω.
Resposta da questão 57:
[E]
O campo magnético é gerado apenas por carga elétrica em movimento.
Resposta da questão 58:
[D]
Usando a regra da mão direita nº 1 (regra do saca-rolha) e a simbologia convencional [entrando
() e saindo ( ) ] e adotando o sentido positivo como saindo, temos:
www.nsaulasparticulares.com.br
Página 56 de 68


 1
1
1 
B  B A  BE  BB 


 B  μ0 i 


 
2 π rA 2 R E 2 π rB
 2  π 4 2  π 2  π 2 

4

 1  16  2 
 15 
B  μ0 i 
 B  4  π  107 

 
 8 π 
 8  π
μ0 i
μ0 i
μ0 i
B  7,5  10 7 T.
Resposta da questão 59:
[D]
À medida que o trabalhador sobe a escada, o fluxo magnético através da esquadria (espira)
aumenta. Pela lei de Lenz, atua na espira uma força para baixo na tendência de anular esse
aumento, fazendo com que o trabalhador sinta a espira "ficar mais pesada".
Resposta da questão 60:
[D]
Dados: m  5,0  1018 kg; q  8,0  106 C, q  4,0  106 m / s, r  5,0  103 cm  5  101 m.
Como é movimento circular uniforme, a força magnética age como resultante centrípeta. Assim:
FM  RCent

q vB 
m v2
r
 B
m v 5  1018  4  106

qB
5  101  8  106

B  5  108 T.
Resposta da questão 61:
[A]
Uma grandeza adimensional é definida como a razão entre medidas de uma mesma grandeza,
como por exemplo, o índice de refração absoluto (n) que é:
velocidade da luz no vácuo c
n
 .
velocidade da luz no meio
v
Resposta da questão 62:
[E]
Utilizando a primeira expressão dada:
E  m gh 
E  kg 


 m 
2
s

m

E  kg 

m2 
 
s2 
E  kg  m2  s2 
Resposta da questão 63:
[C]
Inércia é a resistência natural que um corpo oferece quando se tenta alterar seu estado de
movimento ou de repouso. A medida da Inércia de um corpo é sua massa. Peso é a força que
o campo gravitacional local aplica no corpo.
www.nsaulasparticulares.com.br
Página 57 de 68
Resposta da questão 64:
[D]
Dado: N  2 N; θ  45.
A figura ilustra a situação.
O bloco está sujeito a duas forças: O peso P  e a força aplicada pelo plano F  . Como ele
está em equilíbrio, a resultante dessas forças é nula, ou seja, elas têm mesma intensidade e
sentidos opostos.
Assim, da figura:
F
F
tg 45  at  1  at  Fat  2 N.
N
2
Resposta da questão 65:
[C]
O volume da pepita é:
V = 108 – 100 = 8 cm3.
Calculando a densidade:
d
m 152

V
8
 d  19 g/cm3 .
Resposta da questão 66:
[A]
A força elétrica age como resultante centrípeta sobre a partícula de carga negativa.
Assim:
k Q q mv
F F 


R
R
kQ q
 m v . I
R
2
el
rescent
2
2
A energia do sistema é a soma da energia cinética com a energia potencial elétrica:
m v k Q  q 

2
R
mv kQq
E

. II
2
R
2
E  E E 
pot
cin

2
mv
mv
2
2
Substituindo (I) em (II): E 
2
1
 E   mv .
2
2
www.nsaulasparticulares.com.br
Página 58 de 68
Resposta da questão 67:
[C]
V
kQ 9x109 x6x106

 1,35x104  104 volts
8
r
4x10
Resposta da questão 68:
[A]
A equação do gerador é:
U  ε  r i  U  1,5  0,05 1  1,5  0,05 
U  1,45 V.
Resposta da questão 69:
[E]
O voltímetro deve ser ligado em paralelo com o trecho de circuito onde se quer medir a tensão
elétrica, ou seja, entre os terminais fase e neutro.
O amperímetro para medir a corrente total deve ser instalado no terminal fase ou no terminal
neutro.
O outro amperímetro para medir a corrente na lâmpada deve ser ligado em série com ela.
Resposta da questão 70:
[B]
1ª Solução:
A figura mostra as forças (normal e peso) agindo no ciclista.
A resultante das forças é a componente tangencial do peso.
Aplicando o Princípio Fundamental da Dinâmica, Calculamos o módulo da aceleração escalar
na descida:
 1
Fres  Px  m a  m g sen 30  a  g sen 30  10    a  5 m / s2.
2
Aplicando a equação de Torricelli:
v 2  v02  2 a S  v 2  02  2  5  1.440  v  14.400 
v  120 m / s.
www.nsaulasparticulares.com.br
Página 59 de 68
2ª Solução:
O sistema é conservativo.
Aplicando o teorema da conservação da energia mecânica entre os pontos A e B:
A
B
EMec
 EMec

m v2
1
 m g h  v 2  2 g S sen 30  v  2  10  1.440  
2
2
v  120 m / s.
Resposta da questão 71:
[B]
Notamos que 2 molas seguram o bloco. Desta forma,
2F  elástica   Peso
2k  x  mg
2k   20   80  10
40 k  800
k  800/40  20 N/cm
Resposta da questão 72:
[D]
Dado: P = 300 N
A Figura 1 mostra as forças que agem no nó. Como a caixa está em repouso, a resultante das
forças que agem sobre ela é nula. Então pela regra poligonal, elas devem formar um triângulo,
como mostrado na Figura 2.
Da Figura 2:
sen30 
PB
TB

1 300

2
TB
 TB  600 N.
www.nsaulasparticulares.com.br
Página 60 de 68
Resposta da questão 73:
[A]
Pela conservação da quantidade de movimento:
m v0  2 m v

v
v0
2
Resposta da questão 74:
[A]
Dados: v0 = 4 m/s; F = 2 N; m = 2 kg; v' = -3 m/s.
Aplicando o teorema do impulso ao processo de aceleração:
F Δt
2 6
m Δv  F Δt  Δv 
 v4 
 v  10 m/s.
m
2
Aplicando o teorema do impulso à colisão:
I  m Δv '
 I  m v ' v  I  2 3  10  I  26 N  s.
Calculando a variação da energia cinética na colisão:
ΔEC 

m v'2 m v 2
m 2 2


v'  v
2
2
2




2 3
3  102  9  100 
2
ΔEC  91 J.
Resposta da questão 75:
[C]
Em choque frontal e perfeitamente elástico de dois corpos de mesma massa, eles trocam de
velocidades. Portanto, após o choque, se bola incidente para, a velocidade da bola alvo é 2
m/s.
Resposta da questão 76:
[C]
Como se trata de sistema mecanicamente isolado, ocorre conservação da quantidade de
movimento.
Qfinal  Qincial

Qfinal  3 mv.
Portanto, após as colisões, devemos ter três esferas bolas com velocidade v como mostra a
alternativa [C].
Podemos também pensar da seguinte maneira: as esferas têm massas iguais e os choques
são frontais e praticamente elásticos. Assim, a cada choque, uma esfera para, passando sua
velocidade para a seguinte. Enumerando as esferas da esquerda para a direita de 1 a 5,
temos:
– A esfera 3 choca-se com a 4, que se choca com a 5. As esferas 3 e 4 param e a 5 sai com
velocidade v;
– A esfera 2 choca-se com a 3, que se choca com a 4. As esferas 2 e 3 param e a 4 sai com
velocidade v;
– A esfera 1 choca-se com a 2, que se choca com a 3. As esferas 1 e 2 param e a 3 sai com
velocidade v.
www.nsaulasparticulares.com.br
Página 61 de 68
Resposta da questão 77:
[E]
O Impulso recebido é numericamente igual à "área" entre a linha do gráfico e o eixo t.
2 1
IF 
 4  I F  6 N  s.
2
Se a referida força é a resultante, podemos aplicar o Teorema do Impulso.
I R  ΔQ  I R  m  v  v 0   6  1 v  3  
v  9 m/s.
Resposta da questão 78:
[D]
Supondo que a mencionada força seja a resultante, aplicando o teorema do impulso, vem:
I F  ΔQ  F Δt  ΔQ  F 
ΔQ
20
=

Δt 0,01
F  2  103 N.
Resposta da questão 79:
[E]
A energia cinética é máxima no ponto onde a energia potencial é mínima. Isso ocorre no ponto
de abscissa x  x2 .
Resposta da questão 80:
[A]
No ponto de compressão máxima, a velocidade é nula. Adotando esse ponto como referencial
de altura, nele, a energia potencial gravitacional também é nula. Assim, aplicando a
conservação da energia mecânica.
i
f
EMec
 EMec
 m g h  d 
k d2

2
k
2 m g  h  d
d2
.
Resposta da questão 81:
[B]
No ponto B, a bola possui velocidade e está acima do solo (referencial). Logo ela possui
energia cinética e energia potencial.
Nota: nas alternativas [A] e [E] o enunciado deveria especificar a modalidade de energia.
Resposta da questão 82:
01 + 02 + 08 + 32 = 43.
[01] Correta.
[02] Correta. Dados: h = 5 m; g = 10 m/s2.
Pela conservação da energia mecânica:
m v2
 m gh
2
 v
2 g h  2  10  5  100 
v  10 m/s.
[04] Incorreta. O enunciado não esclarece se Frederico teve sucesso na operação de
www.nsaulasparticulares.com.br
Página 62 de 68
salvamento. Se teve, o choque deve ter sido inelástico.
[08] Correta.
[16] Incorreta. Dados: M = 70 kg; m = 10 kg; v = 10 m/s.
Usando a conservação da quantidade de movimento (Q) no choque inelástico:
depois
Qantes
 M v  M  m  v '  70  10  80 v '
sist  Qsist

v '  8,75 m/s.
[32] Correta. Esse conceito já foi usado na resolução da afirmativa anterior.
Resposta da questão 83:
[D]
Da figura, o comprimento de onda, menor distância entre dois pontos que vibram em fase, é
λ  4m.
Supondo que 8 s seja o menor tempo para que o amigo esteja na posição mais elevada da
onda, o período de oscilação é T = 8 s.
Usando a equação fundamental da ondulatória:
λ 4
v 
 v  0,5 m/s.
T 8
Resposta da questão 84:
[B]
A figura mostra as amplitudes e os comprimentos de onda das duas ondas.
[I] Incorreta. Como mostra a figura, AP  A Q.
[II] Correta. Como mostra a figura, λP  2 λQ.
[III] Incorreta. A onda P tem a metade da frequência da onda Q.
f
vP  vQ  λ P fP  λ Q f Q  2 λQ fP  λ Q f Q  fP  Q .
2
Resposta da questão 85:
[B]
Dados: c = 3  108 m/s; f = 40 MHz = 4  107 Hz.
Da equação fundamental da ondulatória:
λ
v 3  108

f 4  107
 λ  7,5 m.
www.nsaulasparticulares.com.br
Página 63 de 68
Resposta da questão 86:
[B]
Notemos que a escala de nível sonoro cresce de cima para baixo. A área em cinza representa
a região de audição de cada uma das orelhas.
[I] Falsa. Analisando os gráficos, concluímos que sons de frequência 6 kHz e nível sonoro de
20 dB não são ouvidos pela orelha direita, mas o são para o orelha esquerda.
[II] Verdadeira. Os gráficos mostram que sussurros de frequência 0,25 Hz e nível de 15 dB são
ouvidos pelas duas orelhas.
[III] Falsa. A diminuição da capacidade auditiva não ocorre pela degeneração dos ossos
descritos acima, assim como estes não estão na orelha externa e sim no ouvido médio.
www.nsaulasparticulares.com.br
Página 64 de 68
Resposta da questão 87:
[A]
A figura mostra o traçado dos raios, determinando a posição do objeto.
Resposta da questão 88:
[D]
No espelho plano, objeto e respectiva imagem são sempre simétricos em relação ao plano do
espelho. Portanto, a imagem desse objeto localiza-se no ponto 4.
Resposta da questão 89:
[D]
A figura simplifica a situação dada.
No triângulo destacado:
tg θ 
3
 3  θ  60.
1
θ  2 β  180  60  2 β  180  β  60.
www.nsaulasparticulares.com.br
Página 65 de 68
Resposta da questão 90:
[A]
Dados: p = 3 cm; A = 2,5.
Da equação do Aumento Linear Transversal:
A
f
f p
 2,5 
f
f 3

2,5 f  7,5  f  1,5 f  7,5  f 
7,5

1,5
f  5 cm.
Resposta da questão 91:
[A]
Ao incidir radialmente sobre uma superfície circular o raio não sofre desvio,
independentemente do sentido de propagação. Ao sair para o ar, o raio está passando do meio
mais refringente para o menor refringente, afastando-se da normal.
Resposta da questão 92:
[B]
A figura mostra os ângulos de incidência e refração:
Nessa figura:
d
tg r   1  r  45.
d
Aplicando a lei de Snell:
nar sen i  n L sen r  1 sen 60  n L sen 45 
nL 
3
2
 nL
2
2
 nL 
3
2

6
.
2
Resposta da questão 93:
[E]
Q  m c Δθ  300 0,09  2 
Q  54 cal.
www.nsaulasparticulares.com.br
Página 66 de 68
Resposta da questão 94:
[C]
Ao ser submetida ao aquecimento de uma substância pura que esteja no estado sólido,
teremos dois pontos em que a temperatura permanece constante à pressão constante.
Primeiramente há o aquecimento do sólido até o momento em que alcançado o ponto de fusão
onde encontramos duas fases distintas (sólido e líquido) sem que haja alteração da
temperatura (região II do gráfico). Ao derreter todo o sólido, resta apenas o líquido que ao
absorver mais calor aumenta sua temperatura até que a pressão de vapor atinja a pressão
atmosférica (região III), neste ponto estamos diante de mais uma mudança de fase (líquido
para vapor) e a temperatura permanece constante até que todo o líquido vaporize (região IV).
No gráfico temos líquido quando começa a fusão até o término da vaporização, ou seja,
corresponde aos pontos II, III e IV.
Resposta da questão 95:
[A]
Dados: mx  50g; c x  0,26cal / g  C; θx  25C; mc  150g; cc  1cal / g  C; θc  100C.
Trata-se de sistema termicamente isolado. Então:
Qxícara  Qcafé  0  mx c x Δθx  mc c c Δθc  0 
50  0,26  θ  25   150 1 θ  100   0 
0,26 θ  6,5  3 θ  300  0  3,26 θ  306,5 
θ  94 C.
Nota: O examinador provavelmente utilizou o termo “morno” por engano.
Resposta da questão 96:
[B]
Dados: L0  5 m; α  105C1; Δθ  40  20  20 C.
ΔL  L0 α Δθ  5  105  20  103 m  0,1 cm.
d  1  0,1  d  1,10 cm.
Resposta da questão 97:
[C]
Dados: T 1 = 200 °C = 473 K; T2 = 400 °C = 673 K.
Como a transformação é isobárica, aplicando a lei geral dos gases, vem:
V1 V2

T1 T2

V1
V
 2
473 673

V2 673

V1 473

V2
 1,4.
V1
www.nsaulasparticulares.com.br
Página 67 de 68
Resposta da questão 98:
[E]
[I] Incorreta. Como o ciclo é anti-horário, o trabalho é negativo e seu módulo é numericamente
igual a área do ciclo.
[II] Correta. A energia interna (U) é diretamente proporcional ao produto pressão  volume.
Assim: pC VC  pA VA  UC  UA .
[III] Correta. Na transformação A  B, ocorre expansão, indicando que o gás realiza trabalho
(W  0). Como há também aumento da energia interna (ΔU  0).
Pela 1ª Lei da Termodinâmica:
Q  ΔU  W  Q  0  o gás recebe calor.
Resposta da questão 99:
[C]
[Resposta do ponto de vista da disciplina de Física]
Os conceitos básicos da Termodinâmica foram alavancados a partir de 1698 com a invenção
da primeira térmica, uma bomba d'água que funcionava com vapor, criada por Thomas Severy
para retirar água das minas de carvão, na Inglaterra. A partir daí, essa máquina foi sendo cada
vez mais aprimorada com a contribuição de vários engenheiros, inventores e construtores de
instrumentos, como James Watt. Por volta de 1760, a máquina térmica já era um sucesso,
tendo importante contribuição na Revolução Industrial.
[Resposta do ponto de vista da disciplina de História]
A Primeira Revolução Industrial revolucionou a maneira como se produziam as mercadorias,
em especial com a criação de maquinários movidos a vapor. Na Inglaterra da década de 1770,
o mercado de tecidos, os transportes (como trens e navios) e as comunicações funcionavam a
partir de máquina a vapor. Logo, a termodinâmica está relacionada à Revolução Industrial.
Resposta da questão 100:
[D]
Fazendo a correspondência entre as escalas:
T  34
82
T  34
6



 t  34  6 
46  34 14  2
12
12
T  40 C
www.nsaulasparticulares.com.br
Página 68 de 68