Exercício - Colégio Santa Rosa

PROFESSOR(A): Rosylanne Gomes
DISCIPLINA: matemática ( Geometria)
Aluno(a):
Série: 8º ano
Nº
Turma:
Exercício de Fixação
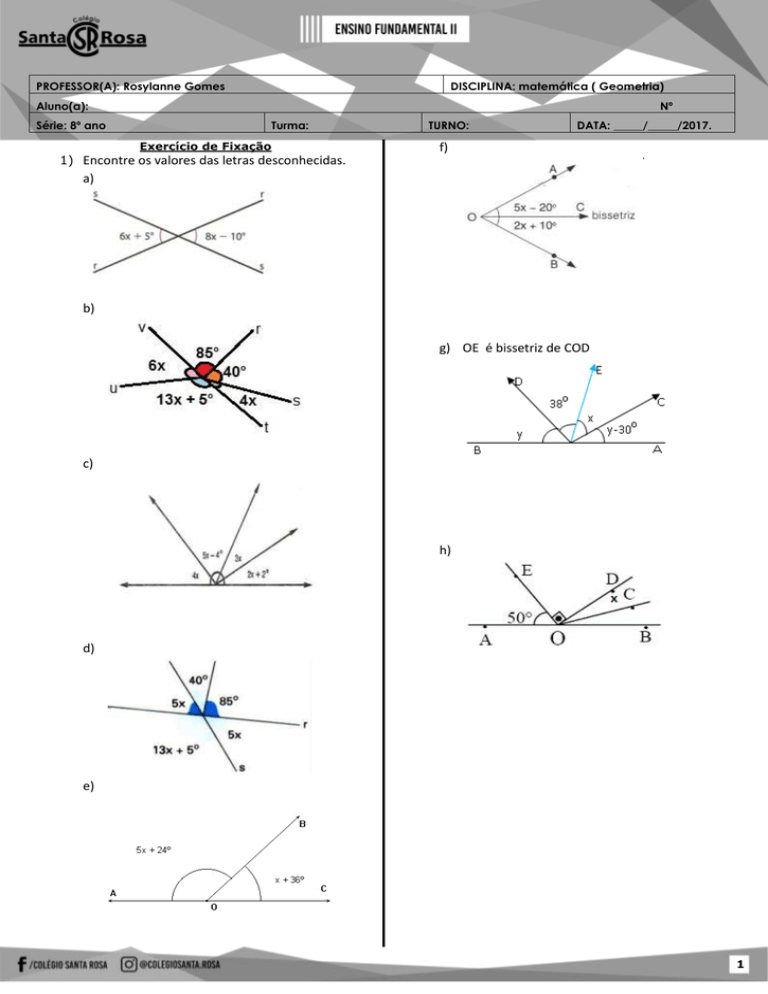
1) Encontre os valores das letras desconhecidas.
TURNO:
DATA: _____/_____/2017.
f)
a)
b)
g) OE é bissetriz de COD
c)
h)
d)
e)
1
Resoluções
1) a) Como são OPV, logo são iguais:
6𝑥 + 5 = 8𝑥 − 10
6𝑥 − 8𝑥 = −10 − 5
−2𝑥 = −15(−1)
2𝑥 = 15
15
𝑥=
2
𝑥 = 7,5
b) A soma de todos os ângulos é igual a
360°, então como temo somente uma
variável x podemos somar e igualar a
360.
6𝑥 + 85 + 40 + 4𝑥 + 13𝑥 + 5 = 360
6𝑥 + 13𝑥 + 4𝑥 = 360 − 85 − 40 − 5
23𝑥 = 230
230
𝑥=
23
𝑥 = 10
c) A soma de todos os ângulos é igual a
180°, como só temos uma variável,
podemos somar e igualar a 180.
4𝑥 + 5𝑥 − 4 + 3𝑥 + 2𝑥 + 2 = 180
4𝑥 + 5𝑥 + 3𝑥 + 2𝑥 = 180 − 2 + 4
14𝑥 = 182
182
𝑥=
14
𝑥 = 13
30
3
𝑥 = 10
𝑥=
g) Se OE é bissetriz de COD, então 𝑥 = 38, como
descobrimos o valor de x, iremos substituir em x
e somar todos os ângulos e igualar a 180º, pois
eles formam um ângulo raso.
𝑦 + 38 + 38 + 𝑦 − 30 = 180
𝑦 + 𝑦 = 180 − 38 − 38 + 30
2𝑦 = 134
134
𝑦=
2
𝑦 = 67
i)
Observe que o ângulo EOD mede 90° e que
OC é bissetriz de DOB, então COD e BOC
são congruentes (iguais), como COD = x,
então BOC = x, e a soma de todos os
ângulos é 180, já que este ângulo é raso.
Com base nessas informações temos:
50 + 90 + 𝑥 + 𝑥 = 180
2𝑥 = 180 − 50 − 90
2𝑥 = 40
40
𝑥=
2
𝑥 = 20
d) Como temos um ângulo raso (180°),
podemos somas os três ângulos
(5x+40+85) e igualar a 180, ou
podemos somar todos os ângulos e
igualar a 360, já que temos uma única
variável x.
5𝑥 + 40 + 85 + 5𝑥 + 13𝑥 + 5 = 360
13𝑥 + 5𝑥 + 5𝑥 = 360 − 40 − 85 − 5
23𝑥 = 230
230
𝑥=
23
𝑥 = 10
e) A soma desses dois ângulos é igual a
180°
5𝑥 + 24 + 𝑥 + 36 = 180°
5𝑥 + 𝑥 = 180 − 24 − 36
6𝑥 = 120
120
𝑥=
6
𝑥 = 20
f) Observe que OC é bissetriz de AOB,
logo, dividiu o ângulo AOB em duas
partes iguais, então:
5𝑥 − 20 = 2𝑥 + 10
5𝑥 − 2𝑥 = 20 + 10
3𝑥 = 30
2