Medidas em Linhas

3 - MEDIDAS nas LINHAS
3.1 - Medida de atenuação da linha

Já foi efectuada a medida da tensão de saída do gerador e ao variar a frequência verificouse a variação da tensão medida com o detector RHO - TECTOR em circuito aberto. (Ver
utilização do reflectómetro)

(Ver figura 3.1). Com o cabo de 9 cm regular a amplitude do gerador para medir uma tensão
Vi = 300 mV a 701.5 MHz. Substitua o cabo de 9 cm por um de 20 m. A tensão detectada
Vout será inferior à Vi. A perda a 701.5 MHz será portanto, em Decibeis: 20 log (Vi / Vout)
FIG. 3.1

Variando apenas a frequência, a perda diminuirá ao descer a frequência, enquanto que
aumentará no caso oposto. Para as frequências mais baixas teremos uma perda com cerca
de 5 dB, e para as mais elevadas cerca de 12 dB.

Somando os valores já determinados anteriormente (ver utilização do reflectómetro) ,isto é,
+2,5 dB a 469.5 MHz e -1,6 dB a 853.5 MHz, que são os erros do sistema de medida,
determina-se a efectiva perda do cabo. Estes valores são devidos às perdas por resistência
dos condutores, com efeito o cabo é delgado, assim como também as perdas no dieléctrico,
que é polietileno sólido.
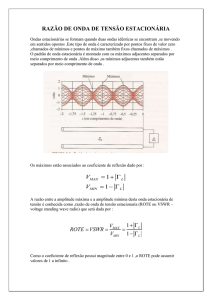
3.2 - Utilização da linha ranhurada : Razão de onda estacionária, máximos e
mínimos de tensão e corrente, comprimento de onda
1
Com a linha ranhurada medem-se directamente tensões e correntes nas diferentes secções de uma
linha coaxial, já que através da linha ranhurada tem-se acesso ao campo eléctrico e magnético
interposto entre os dois condutores que constituem a linha coaxial.
Portanto, em presença de ondas estacionárias são visíveis os máximos e os mínimos da tensão (ou
da corrente); a distância entre um máximo e o mínimo adjacente é igual a um quarto do comprimento
da onda; o factor de velocidade da linha é igual a 1 , já que o dieléctrico é ar.
Medindo a distância entre dois mínimos e multiplicando-a por dois, é conhecendo o factor
velocidade, é possível obter, no caso desta ser desconhecida, a frequência do sinal aplicado na linha
ranhurada.
A Razão da Onda Estacionária (SWR) é igual à razão entre o valor do máximo e o valor do
mínimo; com efeito, em correspondência do máximo somam-se os valores (de tensão ou de
corrente) da onda directa e da onda reflectida, enquanto que em correspondência do mínimo
subtraem-se. Se a onda reflectida não existe, tensão e corrente são constantes em toda a linha
(figura 3.2) e a sua razão é igual ao valor da impedância característica Zo; a SWR vale portanto
1 (normalmente escreve-se : “SWR = 1 : 1”).
FIG. 3.2
2

Regular no valor máximo da potência de saída do gerador, sintonizado nas frequências mais
baixas (por exemplo 509.5 MHz). Ligar a saída do gerador num extremo da linha ranhurada
com o cabo de 75 Ohm e com a extensão de 1 metro.

Terminar com 75 Ohm a extremidade livre da linha ranhurada: a linha fica assim fechada
com sua impedância característica.

Ligar na saída da sonda de tensão um voltímetro de c.c. ou um osciloscópio: medem-se
algumas dezenas de mV. Pode-se ligar também o medidor de campo modo FSM/LA ao
conector RF e efectuar a medida avaliando a luz dos LED.

Se existe uma adaptação perfeita, movendo o carro ao longo da linha ranhurada, a
amplitude do sinal permanece praticamente constante. De todas as maneiras poderão
verificar-se algumas variações devidas à presença dos conectores ou a pequenas variações
do alinhamento do carro.

Substituir o terminal de 75 Ohm por um de 50 Ohm e medir a tensão ao longo da linha. Esta
apresentará mínimos e máximos mais pronunciados do que no caso anterior.

Verificar que a distância entre máximo e mínimo é efectivamente igual ao comprimento da
onda, isto é:


4

v
3  108

 0,58881mts
f 509,5  10 6
0,58881
 0,1472mts  14,72cm
4

Variando a frequência e repetindo as medidas observa-se como a distância entre máximos e
mínimos se alarga ou diminui quando se diminui ou aumenta a frequência.

Repetir a experiência com o terminal de 100 Ohm.

Observe que, com a linha ranhurada, é possível distinguir se a carga é maior ou menor que
a impedância característica da linha. Com efeito, se ligarmos 100 Ohm, o mínimo da tensão
obtêm-se a ¼ de comprimento de onda da carga, enquanto que na carga obtêm-se um
máximo; ligando a terminação de 50 Ohm, o mínimo de tensão encontra-se na carga e em
todas as posições distantes de um número inteiro de comprimentos de onda deste (figura
3.3).
3
FIG. 3.3
As medidas anteriores podem efectuar-se utilizando a sonda de corrente em vez da sonda de
tensão, tendo em conta que, com a carga resistiva, máximos e mínimos de corrente corresponderão
respectivamente a mínimos e máximos de tensão.
Se a impedância de terminação aumenta até ao valor infinito, a linha converte-se aberta, enquanto
que se, se reduzir até ao valor zero, a linha converte-se fechada em curto circuito.
Se a linha estiver terminada em curto circuito, a corrente é máxima (e a tensão nula) na extremidade
da linha, anula-se a distância de um quarto de onda do curto-circuito para de seguida colocar-se
novamente no valor máximo a distância da longitude média da onda (figura 3.4). A tensão comportase do mesmo modo, no entanto desfasada de um quarto de onda, de maneira a que os máximos de
uma correspondem aos mínimos da outra.
4
CURTO CIRCUITO
CIRCUITO ABERTO
FIG.3.4
FIG.3.5
No caso da linha aberta, isto repete-se, no entanto com a diferença de que é a tensão que é máxima
na extremidade da linha, enquanto que a corrente anula-se e o comportamento senoidal (sinusoidal)
repete-se com a corrente e tensão permutadas entre si ( figura 3.5)
O efeito das perdas, quer dizer, o do circuito aberto ou do curto-circuito não perfeitos, pode
determinar um desfasamento adicional entre corrente e tensão, detectável já que a corrente não se
anula completamente em correspondência do máximo de tensão; a correspondência entre máximos
de corrente e mínimos de tensão poderá notar-se de qualquer modo.

Colocar nas extremidades da linha ranhurada um terminal em curto-circuito e procurar as
posições de máximo ou de mínimo da tensão (sonda V). Estas serão colocadas (se a
frequência for de 509.5 MHz) a uma distância de cerca de 14.7 cm entre elas.

Utilizar agora a sonda de corrente (com o cuidado de que a referência variou por motivos de
montagem óbvios). Os máximos da corrente estarão praticamente nas mesmas posições
dos mínimos da tensão e vice-versa.

Colocar o carro num mínimo de corrente (máximo de tensão). Retirar o terminal de curtocircuito deixando a linha aberta. O valor na saída da sonda de corrente passará do mínimo
ao já medido, para os máximos.

Deslocar o carro para levar a sonda de tensão ao mesmo ponto. O valor detectado será
agora cerca de zero, indicando que se encontra num mínimo de tensão.
5

Averiguar, movendo o carro, as posições de máximo e de mínimo. Serão iguais às medidas
anteriores, mas permutadas entre si.
3.3 - Medida do coeficiente de reflexão com a ponte Reflectométrica
A medida pode efectuar-se em correspondência com os simples valores de frequência ou de
maneira panorâmica, utilizando o Sweep num certo intervalo de frequências.
3.3.1 - Medida para simples frequências

Ligar o gerador RF, o rho-tector, os cabos e o multímetro como na figura 3.6.
FIG: 3.6

Predispor o gerador numa certa frequência (por exemplo: 701.5 MHz), introduzir em Z L o
terminal de curto-circuito (de forma a que toda a potência gerada seja reflectida) e regular a
amplitude do gerador de forma a obter uma leitura de 300 m V no multímetro. Esta tensão é
um valor de referência correspondente a uma situação de reflexão total que se apresenta na
extremidade da linha.

Retirar o curto-circuito e em seu lugar ligar um terminal Z L = 75 Ohm.

A razão entre a tensão de referência que agora é medida com o multímetro e a tensão de
referência correspondente à reflexão total ( 300 mV neste caso) é o coeficiente de reflexão
da carga Z L conectado na linha de 75 Ohm. Em teoria, estando em condições de perfeita
adaptação entre linha e carga (ZO = Z L = 75 Ohm), o coeficiente de reflexão teria que ser
nulo.

Inserir Z L = 50 e 100 Ohm. O coeficiente de reflexão aumenta relativamente ao caso
anterior.

Da razão:
6
SWR 
1  RHO
1  RHO
se obtém-se a Razão de Ondas Estacionárias.
Da razão:
Z 0 (1  RHO )

Z1 (1  RHO )
Pode-se conhecer a impedância da carga Z 1, logo após a medida do coeficiente de reflexão RHO e
conhecida a impedância característica da linha.

Efectuar as medidas anteriores com frequências diferentes; reportar logo para um gráfico o
comportamento do coeficiente de reflexão e da SWR ao variar a frequência.
3.3.2 - Medida panorâmica
A medida panorâmica do coeficiente de reflexão (ou das perdas de retorno se o instrumento medidor
estiver calibrado em Decibeis) é muito frequente nos sistemas de transmissão que envolve linhas,
guias de onda e antenas.

Para efectuar este tipo de medida requer-se também um osciloscópio. Conectar o gerador
RF, o rho-tector, os cabos e o osciloscópio segundo a figura 3.7.
FIG. 3.7

Predispor o osciloscópio em modo c.c. e colocar a linha do zero (fig. 3.8) na extremidade
inferior do écran; predispor o gerador numa certa frequência central (por exemplo: 701.5
MHz), inserir em Z L o terminal de curto-circuito (de modo a que toda a potência gerada se
reflicta) e regular a amplitude do gerador e a escala e do osciloscópio de forma a obter um
traço na extremidade superior do écran (figura 3.8).
7
FIG. 3.8
Este traço, gerado pela amplitude da reflexão total nas diferentes frequências, será considerado
como referência. Para manter no écran esta referência, uma técnica utilizada na prática é a de
marcar o traço com um marcador, de forma a fixa-lo no écran.

Retirar o curto-circuito e conectar em seu lugar o terminal Z L = 75 Ohm.

traço reportado para o écran representa o novo valor da potência reflectida ao variar a
frequência. A razão frequência por frequência entre as duas tensões, a acabada de medir e
a de referência, é o coeficiente de reflexão da carga ZL ligada na linha de 75 Ohm. Em
teoria, estando em condições de perfeita adaptação entre linha e carga ( Zo = Z L = 75
Ohm), o traço do sinal reflectido teria que sobrepor-se à linha de zero, portanto o coeficiente
de reflexão teria que ser nulo.

Inserir Z L = 50 e 100 Ohm: o sinal reflectido e por conseguinte o de reflexão, aumentam
relativamente ao caso anterior.
3.4 - Dimensões da linha e impedância característica
Uma linha de transmissão poderá imaginar-se como se fosse composta por elementos infinitesimais
constituídos por indutâncias e capacidades (figura 3..9). A inductância em série expressa a
indutância por unidade de comprimento dos condutores, enquanto que a capacidade expressa a
capacidade entre os condutores da linha. Para ter em conta as perdas, presentes numa linha real,
considera-se também a resistência dos condutores (em série à indutância) e a resistência de perda
do dieléctrico (em paralelo ao condensador) (figura 3.10).
8
Linha Ideal
FIG. 3.9
Linha real
FIG. 3.10
A impedância característica Zo de uma linha é definida como a impedância na qual se tem que
fechar a linha para que se comporte como se fosse de comprimento infinito. Se a linha for real, a
impedância característica vale:
Z0  Z
Y
 ( R  jL) /(G  jC )
Em altas frequências, nas que
impedância característica é:
Z0  L
R  L e G  C , ou então no caso de perdas desprezíveis, a
C
E resulta portanto proporcional à inductância por unidade de comprimento e inversamente
proporcional à capacidade por unidade de comprimento. Praticamente, a inductância diminui se o
diâmetro dos condutores aumenta, enquanto que a capacidade diminui se se aumenta a distância
entre eles.
3.4.1 - Linha bifilar
Uma linha bifilar é constituída por dois condutores, normalmente cilíndricos e paralelos entre si
submergidos num dieléctrico que se supõe ser perfeitamente isótropo, quer dizer, uniforme em todas
as direcções (figura 3.11)
9
Linha Bifilar
FIG. 3.11
Numa linha bifilar submersa num dieléctrico com constante dieléctrica
Zo 
276
r
log
r
, a impedância vale:
2D
d
Nota:
Impedância intrínseca do meio
Z celula 
L
l 
C
l

 Zo

( )
Para o ar ou vácuo:
0
4  10 7 Hm 1

 376.731  120  377
0
8.85  10 12 Fm 1
Zo 
(Resistência intrínseca do
espaço vazio)
sendo
120
 128
e
(e = 2,71828….)
De onde:
D é a separação (distância) dos dois condutores, d é o diâmetro dos condutores e  r a constante
dieléctrica relativa.
Por exemplo:
Para d = 3 mm. e D = 20 mm e se a linha está no ar (  r = 1) :
10
Z 0  276  log
40
 276  1,1  330
3
Numa linha bifilar aumentando a distância entre os condutores, aumenta a impedância
característica. A impedância aumenta também se, se reduzir o diâmetro dos condutores. O
limite da linha bifilar realizável em ar é constituído pela igualdade entre a separação (distância)
e o diâmetro dos condutores: se D = d, a impedância seria:
Zo = 276 log (2) = 83 Ohm
Na realidade a, fórmula resultará menos exacta para razões entre distâncias e diâmetros inferiores a
1 , devido à interacção dos campos electromagnéticos dos dois condutores, e alcançará o valor nulo
(linha em curto-circuito) de maneira progressiva (figura 3.12).
FIG. 3.12

A linha bifilar de baixa impedância (75 Ohm) utilizada para os exercícios, está realizada com
uma distância de 7 mm. Entre os condutores e um diâmetro de 6 mm. A impedância que
resulta está muito perto de 75 Ohm. A linha de impedância mais alta (300 Ohm) foi realizada
com condutores de 3 mm. distanciados de 30 mm.

Para verificar a impedância da linha de 300 Ohm proceda do seguinte modo:
1. Ligar o gerador, a ponte reflectométrica e o transformador (BALUN) 1:4 como na
figura 3.13. O BALUN “transforma” com uma razão de 1:4 a impedância vista nas
extremidades. Os 75 Ohm vistos pelo BALUN até à ponte reflectométrica, são
transformados em 300 Ohm vistos pelos bornes de saída;
11
FIG. 3.13
2. Fechar os bornes do BALUN com 300 Ohm. e observar a diminuição SWR medida;
3. Fechar os bornes do BALUN com a linha de 300 Ohm, fechada por sua vez com a
resistência de 300 Ohm, e observar a diminuição da SWR análoga ao caso anterior;
4. Predispor o gerador de RF mod. LAG/EV para as frequências mais baixas e ligá-lo
directamente ao BALUN 4: I. Inserir o terminal de curto-circuito no final da linha,
aproximar a um dos dois condutores o medidor de tensão-corrente mod. VI/LA e
certificar-se da presença de máximos e mínimos de tensão e corrente devidos à
SWR.
5. A impedância da linha de 75 Ohm é controlada de maneira análoga à anterior,
utilizando o BALUN 1:1 e a linha de 75 Ohm. Também neste caso se podem
verificar os máximos e os mínimos de tensão e corrente ao longo da linha.
3.5 - Transformação de impedâncias
A presença da onda estacionária deve-se à reflexão de potência no extremo da linha; se a linha está
desadaptada no máximo, quer dizer, está aberta ou fechada em curto-circuito, e a reflexão é total.
Uma linha suficientemente curta, de maneira a desprezar as perdas, e terminada na sua impedância
característica, é perfeitamente transparente. Em cada ponto a tensão e a corrente são constantes,
portanto a impedância medida é constante.
12
Se em troca estamos em presença de ondas estacionárias, a tensão e corrente variam ao longo da
linha, repetindo-se com comprimento de onda reduzido relativamente à mesma no ar devido à
diferente velocidade de propagação.
Para cada meio comprimento de onda, o valor da tensão e da corrente é constante,
também em presença de ondas estacionárias. Isto significa que a distância de um
número inteiro de comprimentos de onda da carga, a tensão e a corrente são as mesmas e
portanto a impedância que se pode medir é a da carga desadaptada, para qualquer impedância
característica da linha.
Com efeito, se a linha está aberta, a meia onda da sua ponta encontraremos um ventre de tensão,
devido à soma da onda directa e a reflectida, enquanto que se estiver em curto-circuito,
encontraremos um nodo, quer dizer tensão nula (figura 3.4 e 3.5).
Contudo, a um quarto de onda do fim, numa linha em curto-circuito, encontraremos um ventre
idêntico ao que teremos na onda média de um aberto. Pode-se dizer que uma linha em quarto de
onda transforma a impedância. Já que troços da linha de meio comprimento de onda não
transformam a impedância, espera-se o mesmo comportamento para uma linha 3/4 de onda, 5/4 de
onda, etc.. Isto é válido se a impedância característica da linha é sempre a mesma. Contudo,
teremos um comportamento similar, também se o troço de quarto de onda é de impedância
característica diferente, isto é uma transformação do valor da impedância. Cálculos que não
referimos dão a fórmula zr = Zi . Zo, que proporciona a razão entre impedância característica Zt do
troço de quarto da onda e as impedâncias na entrada e na saída Zi e Zo.

Vejamos uma aplicação do que anteriormente foi exposto utilizando o RHO-TECTOR (figura
3.14). Aplique aprox. 300 mV do sinal, medidos ligando apenas o terminal de 75 Ohm. O
comprimento da linha entre o gerador e RHO-TECTOR não é determinante, usaremos
portanto o cabo de 1 m. ( de Ohm).
FIG. 3.14
No conector Zx ligaremos o cabo de 50 Ohm (no qual se tinha ligado o conector BNC fêmea-fêmea)
comprimento aprox. 43 cm., que corresponde aproximadamente a três meios comprimentos de onda
à volta dos 700 MHz. Tenha sempre presente que o comprimento de onda no cabo tem que ter em
conta o factor de velocidade, que neste cabo é de aprox. 0.66. O comprimento da onda no cabo será
calculada multiplicando por 0.66 o comprimento da onda no ar:
Lc  0,66  La  0,66 
c
f
13
Lc = comprimento de onda no cabo
La = comprimento de onda no ar
c = velocidade da luz = 3  10 m / s
f = frequência do sinal.
8

Ligar o terminal de 75 Ohm e variar a frequência entorno dos 700 MHz, de forma a obter a
leitura mínima no multímetro. Isto significa que, a dada frequência, encontramo-nos em
condições de adaptação também se a linha e a carga têm impedâncias diferentes.

Vejamos agora se é possível usar uma parte da linha como transformador de impedância
(figura 3.15). Usaremos o cabo de 75 Ohm e comprimento aprox. 153 cm. ,correspondente
a 5,25 comprimentos de onda (quer dizer, um múltiplo de  /4) à volta dos 680 MHz.

Portanto, à frequência de 680 MHz, ligando num extremo do cabo de 75 Ohm uma
resistência Z L de 50 Ohm, a impedância Zo no outro extremo vale: .
Z 0  Zt 2 / Zi  5625 / 50  112
Se compararmos esta Zo com uma resistência de 100 Ohm ligada na porta Zn da ponte, teremos
uma SWR de 1 : 1.12 no lugar de 2: I que se obteria com a impedância de 50 Ohm conectada
directamente, ou seja sem linha interposta.

Inserimos agora como Zn o terminal de 100 Ohm; deixamos aberto Zx e regulemos a saída
para 300 mV de leitura a 685.5 MHz.

Ligamos como Zx o terminal de 50 Ohm. A leitura será à volta de 1/3 do valor anterior, ou
seja cerca de 100 m V, correspondentes a uma SWR de 2 : 1.

Inserimos agora o terminal de 50 Ohm no fim do cabo de 153 cm. A leitura é inferior à
anterior, portanto é também inferior a SWR. Isto demonstra que a linha de 75 Ohm com um
numero múltiplo impar de  /4 realiza a adaptação de impedância. A melhor condição de
adaptação obtêm-se ajustando a frequência do gerador, ou seja, fazendo corresponder
exactamente o múltiplo de  /4 com o comprimento da linha.
FIG. 3.15
14
3.6 - SWR em linha com perdas
A potência incidente na carga, no caso da linha com perdas, é inferior à produzida pelo
gerador.
A potência reflectida no percurso de retomo até ao gerador, sofre a mesma atenuação de
percentagem.
lsto significa que, em presença de perdas, ainda no caso da linha com reflexão total, isto é, aberta ou
em curto-circuito, quanto mais se junta ao gerador mais aumentará a medida da tensão directa e
diminuirá a da tensão reflectida (figura 3.16).
O valor dos nodos de tensão(e de corrente), ou seja dos pontos nos quais a tensão reflectida se
junta à da directa (por estar em oposição de fase) não é constante ao longo da linha, aumentando
quanto mais se desloca até ao gerador. Ao contrário, o valor dos ventres, nos quais os dois valores
máximos se somam, permanece praticamente constante se as perdas são principalmente de tipo
resistivo (portanto independentes do valor da tensão).
A razão das ondas estacionárias SWR, também para o caso da linha aberta ou em curto-circuito,
efectivamente é infinito no extremo da linha até à carga, no entanto em presença de perdas varia ao
longo da linha.
No extremo até ao gerador não se mede um coeficiente de reflexão unitária, a não ser que quanto
mais a linha perde, muito mais parecerá adaptada. A perda do cabo de 20 m já foi medida e vale:
8 dB a 469.5 MHz
9 dB a 701.5 MHz
13 dB a 853.5 MHz
Se a 700 MHz o cabo perde aprox. 10 dB, deixando aberta a sua extremidade, a tensão em todo o
percurso gerador-carga-gerador resulta reduzida de 20 dB, ou seja 10 vezes; conclusão, a tensão
reflectida que medimos é de 1/10 da incidente. A SWR que resulta é:
SWR 
1  RHO
1  RHO

1  0,1
 1,22
1  0,1
que corresponde à desadaptação de uma carga de 75 x 1.22 = 91 Ohm ou melhor 75/1.22 = 61 Ohm
numa linha sem perdas.
15
FIG. 3.16
16
Porquê que as impedâncias mais comuns dos cabos coaxiais são de 50 e 75 Ohms?
- A impedância teórica para se obter a atenuação mínima numa linha coaxial é de 77
Ohms, enquanto que a melhor impedância para manusear a máxima capacidade
potência sã 30 Ohms. A media é 53,5 Ohms, a qual é arredondada para 50 Ohms.
- A impedância coaxial de 75 Ohms também é muito usada porque esta está muito
próxima da mínima atenuação que é de 77 Ohms.
17