MÓDULO 11 FRENTE 1 – MECÂNICA

C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 61
FRENTE 1 – MECÂNICA
3. (CESUMAR-2013) – O módulo do vetor soma
→ → → → → →
s = a + b + c + d + e entre os vetores deslocamentos abaixo representados vale
a) 5cm
b) 7cm
c) 8cm
d) 10cm
e) 12cm
MÓDULO 11
VETORES
1. (VUNESP-UEAM-2013) – São exclusivamente grandezas vetoriais:
a) campo elétrico, velocidade, aceleração e força.
b) deslocamento, velocidade, calor e potência.
c) período, frequência, energia e força.
d) aceleração, campo magnético, energia e massa.
e) força, aceleração, tempo e temperatura.
RESOLUÇÃO:
As principais grandezas vetoriais são:
→
1) Deslocamento: d
→
2) Velocidade: V
→
RESOLUÇÃO:
3) Aceleração: a
→
→
→
→
a = 2 i + 4 j (cm)
4) Força: F
→
→
5) Impulso: I = F . t
→
→
→
→
→
→
→
→
→
→
→
→
→
b = –2 i – 2 j (cm)
→
→
c = –2 i (cm)
6) Quantidade de movimento (momento linear): Q = m V
→
7) Campo elétrico: E
d = –2 j (cm)
→
8) Campo magnético: B
e = –2 i + 3 j (cm)
Resposta: A
s = –4 i + 3 j (cm)
→
2. (PUC-MG) – Uma partícula é submetida à ação de duas forças
constantes, uma de intensidade 60N e a outra de intensidade 80N.
Sobre o módulo da força resultante sobre essa partícula, pode-se
afirmar que será
a) de 140N necessariamente.
b) de 20N em qualquer situação.
c) de 100N se as forças forem perpendiculares entre si.
d) obrigatoriamente diferente de 80N.
RESOLUÇÃO:
F2 – F1 F F2 + F1 F2 = 80N e F1 = 60N
= 0°
⇒ FR = 140N
= 180° ⇒ FR = 20N
= 90°
. s . = (3)2 + (4)2
→
. s . = 5cm
Resposta: A
20N FR 140N
FR2 = F12 + F22 ⇒ FR2 = (60)2 + (80)2
FR = 100N
Resposta: C
– 61
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 62
MÓDULO 12
MOVIMENTO CIRCULAR UNIFORME
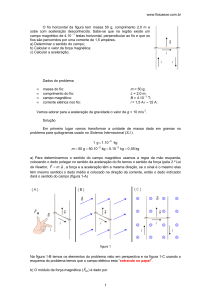
1. (OLIMPÍADA BRASILEIRA DE FÍSICA) – Considere um
relógio analógico com um ponteiro de minutos (ponteiro maior) e outro
menor que indica a hora, como ilustrado na figura abaixo.
a) Determine o comprimento L da circunferência que a extremidade
do ponteiro de minutos circunscreve em 1 hora. Seu valor deve ser
expresso em cm. (use π = 3)
b) Qual a velocidade escalar linear V (suposta constante) da extremidade do ponteiro de minutos em cm/s?
c) Qual a velocidade angular ω do ponteiro das horas em rad/h?
(use π = 3).
RESOLUÇÃO:
a) Em 1h o ponteiro dos minutos dá uma volta completa e portanto:
RESOLUÇÃO:
Δs
2πR
→
a) V = ––– = –––––
Δt
T
→
2 . 3,1 . 1,5 . 1011m
V = –––––––––––––––––– = 3,0 . 104m/s ⇒
3,1 . 107s
V2
9,0 . 108
b) →
a = ––– = –––––––––– (m/s2) ⇒
R
1,5 . 1011
c)
→
V = 30km/s
→
a = 6,0 . 10–3m/s2
3. (VUNESP-UEA-2013-MODELO ENEM) – O trator mostrado
na figura move-se em linha reta, com velocidade constante e sem
escorregar sobre uma superfície plana e horizontal.
L = 2πR = 2 . 3 . 2,0cm
L = 12,0cm
Δs
2πR
12,0cm
12,0cm
b ) V = ––– = ––––– = ––––––– = –––––––
Δt
T
1,0h
3600s
V 3,3 . 10–3cm/s
(www.pt.dreamstime.com. Adaptado.)
Δϕ
2π
6
c ) = ––– = ––– = ––– rad/h
Δt
Th
12
= 0,50rad/s
Respostas: a) L = 12,0cm
b) V = 3,3 . 10–3cm/s
c) = 0,50rad/h
Considerando-se as medidas mostradas e sabendo-se que as rodas dianteiras do trator dão uma volta completa em 1,25 segundo, é correto
afirmar que a frequência de rotação, em hertz, das rodas traseiras do
trator é igual a
a) 0,3
b) 0,4
c) 0,5
d) 0,6
e) 0,7
RESOLUÇÃO:
Δs
2πR
V = ––– = –––– = 2π f R
Δt
T
2π fT RT = 2π fD RD
2. Considere a órbita da Terra em torno do Sol como circular com
raio R = 1,5 . 1011m e período T = 1 ano 3,1 . 107s. Adotando-se
= 3,1 pede-se:
a) determinar o módulo da velocidade orbital da Terra em torno do
Sol. Dar a resposta em km/s.
b) determinar o módulo da aceleração vetorial da Terra em seu
movimento orbital.
→
c) fazer uma figura representando os vetores velocidade V e aceleração →
a em uma dada posição da órbita.
62 –
fT DT = fD DD
DD
fT DT = –––
TD
1,0
fT . 1,6 = –––– ⇒
1,25
Resposta: C
fT = 0,5Hz
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 63
MÓDULO 13
BALÍSTICA
1. Considere que uma bola de futebol, lançada obliquamente como
ocorre num tiro de meta, descreve uma parábola.
A figura a seguir representa esta situação.
Uma bola foi lançada com uma velocidade inicial de módulo
V0 = 72km/h e ângulo de lançamento tal que sen = 0,80 e
cos = 0,60.
(Adote g = 10m/s2)
Determine:
a) a altura máxima H atingida pela bola;
b) a distância horizontal D que a bola percorreu até voltar ao solo.
RESOLUÇÃO:
a) 1) V0y = V0 sen = 20 . 0,80 (m/s)
V0y = 16m/s
2)
2
Vy2 = V0y
+ 2y Δsy
0 = 256 + 2 (–10) H
H = 12,8m
b) 1)
Vy = V0y + y t
0 = 16 – 10 . ts
ts = 1,6s
T = ts + tq = 3,2s
2)
V0x = V0 cos V0x = 20 . 0,60 (m/s) = 12m/s
3)
Δsx = Vx t
D = 12 . 3,2 (m)
2. (UFTM-MG-2013) – Em um gramado plano e horizontal, João e
Pedrinho brincam com o jogo de peteca.
Para mandar a peteca para João, Pedrinho dá uma pancada com a mão
espalmada, imprimindo a ela uma velocidade inicial de módulo
V0 = 10,0m/s, em uma direção que faz 60° com a horizontal, conforme
a figura.
João, que está a 8,5m de Pedrinho, apanha a peteca na mesma altura h
em que ela partiu. Desprezando-se a resistência do ar, adotando-se
1
3
g = 10,0m/s2, cos 60° = ––– e sen 60° = –––– , calcule:
2
2
a) o intervalo de tempo entre Pedrinho acertar a peteca e João pegála.
b) a altura em que a peteca estará, em relação ao nível horizontal de
onde partiu, no instante em que sua velocidade vetorial fizer um
ângulo de 45° com a horizontal.
RESOLUÇÃO:
a) 1)
2)
3
3 m/s
V0y = V0 sen 60° = 10,0 –––– m/s = 5,0 2
Vy = V0y + y t ↑ 3
5,0 0 = 5,0 3 – 10,0tS ⇒ tS = ––––––– ⇒
10,0
3)
T = tS + tQ = 2tS ⇒
3
ts = –––– s
2,0
T = 3s
b) 1)
= 45°
Vy = V0x = V0 cos 60° = 5,0m/s
D = 38,4m
Respostas: a) 12,8m
b) 38,4m
2)
2
Vy2 = V0y
+ 2 y sy
25,0 = 75,0 + 2 (–10,0) H
H = 2,5m
Respostas: a) 3 s ou 1,7s
b) 2,5m
– 63
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 64
3. (VUNESP-2013-MODELO ENEM) – Um avião de treinamento
militar voa horizontalmente, em linha reta, a uma altitude relativa ao
solo de 500m, com velocidade constante de módulo 180km/h. Seu
piloto solta um artefato quando se encontra na mesma vertical de um
veículo no solo, que também se desloca horizontalmente, no mesmo
sentido do voo do avião, e com velocidade de módulo 72km/h no
instante de soltura do artefato, mas em movimento uniformemente
acelerado. Para que o artefato atinja o veículo no solo, este deverá estar
dotado de uma aceleração escalar expressa em m/s2, de
a) 4,0.
b) 5,0.
c) 6,0.
d) 7,0.
e) 8,0.
Dado: Adota-se a aceleração da gravidade local com módulo igual a
10m/s2 e despreza-se a resistência do ar.
RESOLUÇÃO:
1) Cálculo do tempo de queda:
γy 2
sy = V0y t + –––
t ↓
2
10
500 = 0 + ––– T2
2
T = 10s
2) Distância horizontal percorrida pelo projétil:
Δsx = Vx t (MU)
D = 50 . 10 (m) ⇒
D = 500m
3) Cálculo da aceleração escalar do veículo:
γ
s = V0 t + ––– t2 (MUV)
2
γ
500 = 20 . 10 + ––– . 100
2
300 = 50 γ
γ = 6,0m/s2
Resposta: C
64 –
MÓDULO 14
1.a E 2.a LEIS DE NEWTON
1. (ENEM) – Em 1543, Nicolau Copérnico publicou um livro
revolucionário em que propunha a Terra girando em torno do seu
próprio eixo e rodando em torno do Sol. Isso contraria a concepção
aristotélica, que acredita que a Terra é o centro do universo. Para os
aristotélicos, se a Terra gira do oeste para o leste, coisas como nuvens
e pássaros, que não estão presas à Terra, pareceriam estar sempre se
movendo do leste para o oeste, justamente como o Sol. Mas foi Galileu
Galilei que, em 1632, baseando-se em experiências, rebateu a crítica
aristotélica, confirmando assim o sistema de Copérnico. Seu argumento, adaptado para a nossa época, é: se uma pessoa, dentro de um
vagão de trem em repouso, solta uma bola, ela cai junto a seus pés.
Mas se o vagão estiver se movendo com velocidade constante, a bola
também cai junto a seus pés. Isto porque a bola, enquanto cai, continua
a compartilhar do movimento do vagão.
O princípio físico usado por Galileu para rebater o argumento
atistotélico foi
a) a lei da inércia.
b) ação e reação.
c) a segunda Lei de Newton.
d) a conservação da energia.
e) o princípio da equivalência.
RESOLUÇÃO:
De acordo com a lei da inércia (1.a Lei de Newton) a bola tende a manter sua
velocidade horizontal constante por inércia pois nenhuma força horizontal
atua na bola durante sua queda (resistência do ar desprezível).
Resposta: A
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 65
2. (UFRN-2013-MODELO ENEM) – As Leis de Newton descrevem os movimentos que podemos executar cotidianamente, tais como
andar, correr, saltar, bem como o fato de, usando máquinas (p. ex.,
aviões), poder voar. As histórias em quadrinhos estão cheias de superheróis com poderes incríveis associados ao ato de voar, como, por
exemplo, o Super-homem e o Homem de Ferro (representados na
figura abaixo).
3. (USF-SP-MODELO ENEM) – Muito se falou sobre o fato de,
em 2012, completar 10 anos da queda das “torres gêmeas” em New
York, num ataque terrorista que nem os mais criativos diretores da
indústria do cinema seriam capazes de imaginar. Foram dois aviões
que colidiram nos edifícios num intervalo de tempo de 15 minutos.
Disponível em <www.superherouniverse.com>. Acesso em: 18 de ago. 2012.
Esses dois super-heróis conseguem voar, entretanto
a) o Homem de Ferro viola a Lei da Inércia, por usar propulsores para
voar.
b) o Super-homem viola a Lei da Ação e Reação, por não usar
propulsores para voar.
c) o Homem de Ferro viola a Lei da Ação e Reação, por usar
propulsores para voar.
d) o Super-homem viola a Lei da Inércia, por não usar propulsores
para voar.
e) os dois super-heróis violam a Lei da Inércia.
RESOLUÇÃO:
O super-homem viola a 1.a Lei de Newton (Lei da Inércia) porque nenhum
corpo pode sozinho mudar sua velocidade vetorial; o corpo deve receber
uma força externa no caso do sistema de propulsores.
Resposta: D
FONTE: >fotosimagens.net> Acesso em: 10/10/2011.
O primeiro deles, um Boeing 767-223, que é capaz de apresentar na
decolagem uma massa de 180 toneladas, apresentava uma velocidade
escalar aproximada de 720km/h no momento do impacto e num
intervalo de tempo de 1,5s foi desacelerado até parar completamente e
se alojar no edifício. Supondo-se que ele apresentasse a massa acima
mencionada, a intensidade da força média no impacto do avião com o
prédio é da ordem de grandeza de
a) 104 N.
b) 105 N.
c) 106 N.
d) 107 N.
e) 108 N.
RESOLUÇÃO:
PFD:
.V.
Fm = m .am. = m –––––
t
200
Fm = 180 . 103 –––– (N)
1,5
Fm = 24 . 106N
Fm = 2,4 . 107N
2,4 < ⇒ ordem de grandezas 107N
10
Resposta: D
– 65
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 66
MÓDULO 15
PESO DE UM CORPO E 3.a LEI DE NEWTON
1.
(UEPB-MODELO ENEM) – Leia com atenção a seguinte tira:
2. (UFPR-2013) – Recentemente, foi publicada em um jornal a seguinte ocorrência: um homem pegou uma sacola plástica de supermercado, encheu com um litro de água e abandonou-a do oitavo andar de
um prédio. A sacola caiu sobre um automóvel que estava estacionado
no nível da rua. Admitindo-se que cada andar do prédio tenha uma
altura de 2,5m e que a sacola de água tenha sido freada pelo capô do
carro em aproximadamente 0,01s, calcule o módulo da força normal
média de frenagem exercida pelo capô sobre a sacola. Despreze a
resistência do ar, o peso da sacola vazia e correções referentes ao
tamanho do carro e ao fato de a sacola não se comportar exatamente
como um corpo rígido. Considere g = 10,0m/s2 e 2 = 1,4
RESOLUÇÃO:
PFD (sacola):
A partir da leitura, analise as proposições a seguir:
I. A resposta que Garfield deu ao seu dono está fisicamente incorreta,
pois o peso de um corpo independe do local onde se encontra.
II. A resposta que Garfield deu ao seu dono está fisicamente correta,
porque, dependendo do local onde o corpo se encontre, o seu peso
se altera.
III.Para Garfield conseguir o seu objetivo, deveria ir a qualquer um destes
planetas do sistema solar: Netuno (campo gravitacional: 10,6N/kg),
Urano (campo gravitacional: 11,0N/kg), Vênus (campo gravitacional:
8,9N/kg), Marte (campo gravitacional: 3,9N/kg).
Com base na análise feita, assinale a alternativa correta:
a) Apenas as proposições I e III são verdadeiras.
b) Apenas as proposições II e III são verdadeiras.
c) Apenas a proposição I é verdadeira.
d) Apenas a proposição II é verdadeira.
e) Nenhuma das proposições é verdadeira.
RESOLUÇÃO:
I. Falsa. A massa independe do local; o peso é proporcional ao módulo da
aceleração da gravidade local.
II. Correta.
III.Falsa. O gato deveria ir para um planeta onde a aceleração da gravidade
fosse menor que a da Terra; nos exemplos citados: Vênus e Marte.
Resposta: D
.ΔV.
1) FN – P = m am = m –––– (1)
Δt
2) Cálculo da velocidade
V2 = V02 + 2γ Δs ↓ V12 = 0 + 2 . 10,0 . 2,5
V12 = 50,0 ⇒
V1 = 5,0 2 (m/s) = 7,0m/s
7,0
3) Em (1): FN – 1,0 . 10,0 = 1,0 . ––––
0,01
FN – 10,0 = 700
FN = 710N
Resposta: 710N
3. (ENEM) – Durante uma faxina, a mãe pediu que o filho ajudasse,
deslocando um móvel para mudá-la de lugar. Para escapar da tarefa, o
filho disse ter aprendido na escola que não poderia puxar o móvel, pois
a Terceira Lei de Newton define que se puxar o móvel, o móvel o
puxará igualmente de volta, e assim não conseguirá exercer um força
que possa colocá-la em movimento.
Qual argumento a mãe utilizará para apontar o erro de interpretação
do garoto?
a) A força de ação é aquela exercida pelo garoto.
b) A força resultante sobre o móvel é sempre nula.
c) As forças que o chão exerce sobre o garoto se anulam.
d) A força de ação é um pouco maior que a força de reação.
e) O par de forças de ação e reação não atua em um mesmo corpo.
RESOLUÇÃO:
As forças de ação e reação são forças trocadas entre dois corpos; nunca
estão aplicadas ao mesmo corpo e nunca se equilibram.
Resposta: E
66 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 67
4. (UDESC-2013) – Um objeto em queda livre encontra-se nas
proximidades da superfície da Terra. Com base nas Leis de Newton, é
correto afirmar que a força peso que atua sobre o objeto:
a) possui par de reação localizado no centro da Terra, tal que apenas
o objeto é acelerado.
b) possui par de reação localizado no centro da Terra, tal que o objeto
e a Terra são acelerados.
c) possui par de reação localizado na superfície da Terra, tal que
apenas o objeto é acelerado.
d) não possui par de reação, já que não há contato com a superfície.
e) possui par de reação localizado no centro da Terra, tal que o objeto
e a Terra não são acelerados.
RESOLUÇÃO:
O peso é a força gravitacional que o planeta Terra aplica no centro de gravidade do objeto. A reação ao peso é a força gravitacional que o objeto aplica no centro da Terra. A ação acelera o objeto e a reação acelera a Terra.
c) De acordo com a 3.a Lei de Newton:
→
→
→
→
FBA = – FAB ⇒ | FBA| = | FAB | = 2,0N
Respostas: a) 2,0m/s2.
b) Horizontal; para a direita; módulo igual a 2,0N.
c) Horizontal; para a esquerda; módulo igual a 2,0N.
2. (FCC) – Quatro caixas, presas por três fios, são puxadas sobre
uma superfície horizontal desprovida de atrito, por meio de uma força
→
F horizontal e de intensidade 100N:
mobjeto aobjeto = mTerra . aTerra
Resposta: B
MÓDULO 16
APLICAÇÕES DAS LEIS DE NEWTON
1. O bloco A, de massa 4,0kg, e o bloco B, de massa 1,0kg, representados na figura, estão justapostos e apoiados sobre uma superfície
plana e horizontal. Eles são acelerados pela força constante e horizontal
→
F, de módulo igual a 10,0N, aplicada ao bloco A, e passam a deslizar
sobre a superfície com atrito desprezível.
A tração no fio 2 tem intensidade 40,0N e são conhecidas as massas
m1 = 4,0kg, m3 = 5,0kg e m4 = 3,0kg.
Nessas condições, a massa m2 e o módulo da aceleração das caixas
são, respectivamente:
a) 8,0kg e 5,0m/s2
b) 7,0kg e 4,0m/s2
2
c) 6,0kg e 3,0m/s
d) 2,0kg e 2,0m/s2
2
e) 1,0kg e 1,0m/s
RESOLUÇÃO:
1) PFD (3 + 4):
T2 = (m3 + m4) a
40,0 = 8,0 a
a = 5,0m/s2
a) Calcule o módulo da aceleração dos blocos.
→
b) Determine a direção e o sentido da força FAB exercida pelo bloco A
sobre o bloco B e calcule o seu módulo.
→
c) Determine a direção e o sentido da força FBA exercida pelo bloco B
sobre o bloco A e calcule o seu módulo.
2) PFD (1 + 2 + 3 + 4):
F = (m1 + m2 + m3 + m4) a
100 = (4,0 + m2 + 5,0 + 3,0) . 5,0
20,0 = 12,0 + m2
m2 = 8,0kg
Resposta: A
RESOLUÇÃO:
a) PFD (A + B):
F = (mA + mB)a
10,0 = (4,0 + 1,0) a ⇒
a = 2,0m/s2
b)
PFD (B): FAB = mBa
FAB = 1,0 . 2,0(N) = 2,0N
– 67
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 68
3. Na situação física da figura seguinte, dois blocos de massas
m1 = 8,0kg e m2 = 2,0kg estão presos a um dinamômetro.
→
Aplicam-se uma força F1 de intensidade 10,0N ao bloco de massa m1 e
→
uma força F2 de intensidade 50,0N ao bloco de massa m2.
Desprezando-se a massa do dinamômetro, determine
a) o módulo da aceleração do sistema;
b) o resultado que deve mostrar o dinamômetro.
A força tensora TM no ponto médio da corda vai acelerar o bloco B e
metade da corda.
mC
C
PFD B + ––– : TM = mB + –––– a
2
2
(
)
(
)
TM = (1,0 + 1,0) . 2,0 (N)
TM = 4,0N
Obs.: considere que o sistema esteja livre de ações gravitacionais.
Resposta: C
RESOLUÇÃO:
a) PFD (sistema):
F2 – F1 = (m1 + m2) a
40,0 = 10,0 . a ⇒
a = 4,0m/s2
MÓDULO 17
b)
APLICAÇÕES DAS LEIS DE NEWTON
PFD (m2): F2 – T = m2a
50,0 – T = 2,0 . 4,0
T = 42,0N
A resultante no dinamômetro é sempre nula (massa desprezível), e a
força que ele indica é a força aplicada em uma de suas extremidades
(força de tração no fio).
1. Considere dois blocos, A e B, de massas mA = 2,0kg e mB = 3,0kg,
conectados por um fio (1) e suspensos verticalmente por um fio (2).
Os fios têm massas desprezíveis e suportam
uma força tensora máxima de 70,0N sem se
romperem.
O sistema tem uma aceleração constante,
vertical, dirigida para cima e de módulo a.
A intensidade da força tensora no fio (1) vale T1.
Despreze o efeito do ar e adote g = 10,0m/s2.
Para que nenhum dos fios arrebente, os
máximos valores de a e T1 são:
a) 4,0m/s2 e 70,0N
b) 14,0m/s2 e 42,0N
c) 14,0m/s2 e 12,0N
d) 8,0m/s2 e 24,0N
e) 4,0m/s2 e 42,0N
Respostas: a) 4,0m/s2
b) 42,0N
4. Considere dois blocos, A e B, ligados por uma corda homogênea
de massa mC = 2,0kg em um local isento de gravidade.
Os blocos A e B têm massas respectivamente iguais a mA = 3,0kg e
mB = 1,0kg.
→
Uma força F constante e de intensidade F = 12,0N é aplicada em A,
conforme mostra o esquema.
A força tensora no meio da corda tem intensidade igual a:
a) zero
b) 2,0N
c) 4,0N
d) 6,0N
e) 12,0N
RESOLUÇÃO:
Aplicando-se a 2.ª Lei de Newton ao sistema (A + C + B), vem:
F = (mA + mC + mB) a
12,0 = 6,0a ⇒
68 –
a = 2,0m/s2
RESOLUÇÃO:
A força aplicada pelo fio (2) acelera o sistema (A + B), e a força aplicada
pelo fio (1) acelera o bloco (B); portanto: T2 > T1.
A condição limite para que os fios não arrebentem é que
T2 = 70,0N.
Aplicando-se a 2ª Lei de Newton ao sistema (A + B), vem:
T2 – (PA + PB) = (mA + mB) a
70,0 – 50,0 = 5,0 . a ⇒
a = 4,0m/s2
Aplicando-se a 2ª Lei de Newton ao bloco B, vem:
T1 – PB = mB a
T1 – 30,0 = 3,0. 4,0 ⇒
Resposta: E
T1 = 42,0N
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 69
2. (UFPR) – Inicialmente, uma caixa A de 20 kg apoiada no alto de
um edifício está presa por um fio a outra caixa, B, de 30 kg suspensa
na lateral do edifício, conforme figura abaixo.
3. (UEG-GO) – Na figura abaixo, os blocos A e B encontram-se
apoiados sobre uma superfície horizontal sem atrito. O bloco C está
ligado ao bloco A por meio de um fio inextensível que passa por uma
polia de massa desprezível. Sendo as massas MA = 4,0kg, MB = 1,0kg e
MC = 5,0kg e considerando-se a aceleração da gravidade com módulo
g = 10,0m/s2, podemos afirmar que
a) o conjunto de blocos A, B e C está em movimento retilíneo uniforme.
b) como a soma das massas dos blocos A e B é igual à massa do bloco
C, o sistema se encontra em repouso.
c) a intensidade da força de contato que A exerce em B e o módulo da
aceleração dos blocos são, respectivamente, iguais a 5,0N e 5,0m/s2.
d) a força de tração que o bloco C exerce no fio tem intensidade de
10,0N.
e) a força que traciona o fio tem intensidade igual a 50,0N.
Quando o sistema é solto, observa-se uma movimentação das caixas.
Desprezando-se as massas do fio e da roldana, considerando-se o sistema sem atrito e g = 10m/s2, o módulo da aceleração do sistema e a
intensidade da força de tração no fio valem, respectivamente:
a) 2,0m/s2 e 100N.
b) 3,0m/s2 e 95N.
c) 4,0m/s2 e 150N.
d) 5,0m/s2 e 130N.
e) 6,0m/s2 e 120N.
RESOLUÇÃO:
RESOLUÇÃO:
1) PFD (A + B + C): PC = (MA + MB + MC)a
50,0 = 10,0 a ⇒
2) PFD (B):
1) PFD (A): T = mAa
(1)
2) PFD (B): PB – T = mBa
(2)
FAB = 5,0N
T = (MA + MB) a
T = 5,0 . 5,0 (N) ⇒
3) PFD (A + B): PB = (mA + mB) a
(1) + (2):
FAB = MBa
FAB = 1,0 . 5,0 (N) ⇒
3) PFD (A + B):
a = 5,0m/s2
T = 25,0N
Resposta: C
300 = 50 . a
a = 6,0 m/s2
4) Em (1): T = 20 . 6,0 (N)
T = 120 N
Resposta: E
– 69
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 70
4. (MODELO ENEM) – Um pêndulo é colocado no aerofólio
traseiro de um carro de Fórmula 1. Num dado intervalo de tempo, em
um trecho retilíneo da pista, esse pêndulo forma um ângulo de 45° com
a vertical. Se o módulo da aceleração da gravidade vale 10,0m/s2, então
o módulo da aceleração do carro, no intervalo de tempo considerado,
em m/s2, vale:
a) 20,0
b) 10,0
c) 7,5
d) 5,0
e) 2,5
RESOLUÇÃO:
RESOLUÇÃO:
1) Quando a aceleração é dirigida para cima:
FN – P = ma
1) Ty = P = mg
2) Tx = ma (PFD)
FN = mg + ma = m ( g + a)
Tx
ma
3) tg = ––– = ––––
Ty
mg
gaparente
FN = 80,0 (10,0 + 3,0) (N) ⇒
a = g tg a = 10,0 . 1 (m/s2)
2) Quando a aceleração
dirigida para baixo:
FN = 1040N
é
P – FN = ma
FN = mg – ma = m (g – a)
a = 10,0m/s2
gaparente
FN = 80,0 (10,0 – 3,0) (N) ⇒
Resposta: B
FN = 560N
3) Quando a aceleração do elevador é nula
(subindo ou descendo em MRU):
FN = P = mg = 80,0 . 10,0N ⇒
FN = 800N
4) Elevador em queda livre:
↓→
a =→
g ⇒ gap = 0
FN = 0
a) Verdadeira.
b) Verdadeira:
MÓDULO 18
APLICAÇÕES DAS LEIS DE NEWTON
1. Uma pessoa de massa = 80,0kg está sobre uma balança, dentro
de um elevador, numa região em que g = 10,0m/s2. Supondo-se que o
mostrador da balança esteja graduado em newtons, assinale a alternativa incorreta.
a) A indicação da balança, quando o elevador está em repouso ou sobe
com velocidade constante, é 800N.
b) Com o módulo da aceleração do elevador igual a 3,0m/s2, a
indicação da balança, quando o elevador sobe com movimento
acelerado, é 1040N.
c) Com o módulo da aceleração do elevador igual a 3,0m/s2, a pessoa
sente-se mais pesada quando o elevador sobe com movimento
retardado.
d) Com o módulo da aceleração do elevador igual a 3,0m/s2, a
indicação da balança, quando o elevador desce com movimento
retardado, é 1040N.
e) A indicação da balança, quando o elevador cai em queda livre, é
zero.
70 –
→
c) Falsa: ↑ V
→
↑ V ↑→a
↓→a
→
d) Verdadeira: ↓ V
e) Verdadeira.
Resposta: C
⇔ gap = g – a ⇔ Pap = 560N e a pessoa sente-se mais
leve
↑→a
⇔ gap = g + a ⇒ FN = 1040N
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 71
2. (VUNESP-2013) – Um bloco de massa M igual a 5,0kg está
pendurado no teto de um elevador por uma corda, na qual um dinamômetro D está associado, de modo a registrar a intensidade da força
de tração que lhe é aplicada, conforme mostra a figura.
RESOLUÇÃO:
1) PFD (1): T – P1 = m1 a (1)
2) PFD (2): P2 – T = m2 a (2)
3) PFD (1 + 2): P2 – P1 = (m1 + m2) a
30,0 – 20,0 = 5,0a
a = 2,0m/s2
4) Em (1):
T – 20,0 = 2,0 . 2,0
T = 24,0N
Resposta E
Sabe-se que a corda e o dinamômetro são ideais e que a aceleração da
gravidade no local tem módulo igual a 10,0m/s2. Nessas condições,
quando o elevador estiver acelerando para baixo com aceleração de
módulo igual a 2,0m/s2, a leitura no dinamômetro, em newtons, será
a) 10,0
b) 20,0
c) 30,0
d) 40,0
e) 50,0
RESOLUÇÃO:
PFD:
P – Fdin = ma
Fdin = mg – ma
Fdin = m (g – a)
gaparente
Fdin = 5,0 (10,0 – 2,0) (N)
Resposta D
Fdin = 40,0N
4. (MODELO ENEM) – Um homem está sentado em um elevador
de pintor sustentado por uma corda ideal que passa por uma polia ideal,
conforme mostra a figura.
A massa total do homem com o elevador
é de 100kg.
Adote g = 10m/s2 e despreze o efeito do
ar.
O homem puxa a corda de modo que o
sistema adquira uma aceleração constante
→
a, vertical, dirigida para cima e de
módulo igual a 1,0m/s2.
A intensidade da força com que o homem
puxa a corda vale:
a) 1100N
d) 500N
b) 1000N
e) 330N
c) 550N
RESOLUÇÃO:
PFD: 2T – P = M a
2T – 100 . 10 = 100 . 1,0
3. (EFOMM-2013) – Na máquina de Atwood representada na figura
M1 = 2,0kg e M2 = 3,0kg.
2T = 1100 ⇒
T = 550N
Resposta: C
Assumindo que o fio é inextensível e tem massa desprezível, assim
como a polia, a intensidade da força de tração no fio, em newtons, é:
a) 6,0
b) 9,0
c) 12,0
d) 18,0
e) 24,0
Dado: g = 10,0m/s2. O efeito o ar é desprezível.
– 71
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 72
FRENTE 2 – TERMOLOGIA E ÓPTICA
MÓDULO 11
(II)Para o sistema de alavanca do ponteiro:
DILATAÇÃO TÉRMICA
DOS SÓLIDOS E DOS LÍQUIDOS
1. (FUVEST) – Para ilustrar a dilatação dos corpos, um grupo de
estudantes apresenta, em uma feira de ciências, o instrumento
esquematizado na figura abaixo. Nessa montagem, uma barra de
alumínio com 30cm de comprimento está apoiada sobre dois suportes,
tendo uma extremidade presa ao ponto inferior do ponteiro indicador
e a outra encostada num anteparo fixo. O ponteiro pode girar
livremente em torno do ponto O, sendo que o comprimento de sua parte
superior é 10cm e, o da inferior, 2cm.
ᐉponteiro
––––––––
ᐉ
=
10cm
––––––
2cm
2ᐉponteiro = 10 . 1,2(mm)
ᐉponteiro = 6mm
Resposta: C
Se a barra de alumínio, inicialmente à temperatura de 25°C, for
aquecida a 225°C, o deslocamento da extremidade superior do ponteiro
será, aproximadamente, de
a) 1mm.
b) 3mm.
c) 6mm.
d) 12mm. e) 30mm.
NOTE E ADOTE
Coeficiente de dilatação linear do alumínio:
2 x 10–5 °C–1.
RESOLUÇÃO:
(I) Cálculo do deslocamento da parte inferior do ponteiro (ᐉ):
ᐉ = ᐉ0 . . ᐉ = 30 . 2 . 10–5 (225 – 25) (cm)
ᐉ = 60 . 10–5 . 200 (cm)
ᐉ = 0,12cm
ᐉ = 1,2mm
72 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 73
2. (UDESC) – Em um dia típico de verão utiliza-se uma régua
metálica para medir o comprimento de um lápis. Após medir esse
comprimento, coloca-se a régua metálica no congelador a uma
temperatura de – 10°C e esperam-se cerca de 15 min para, novamente,
medir o comprimento do mesmo lápis. O comprimento medido nesta
situação, com relação ao medido anteriormente, será:
a) maior, porque a régua sofreu uma contração.
b) menor, porque a régua sofreu uma dilatação.
c) maior, porque a régua se expandiu.
d) menor, porque a régua se contraiu.
e) o mesmo, porque o comprimento do lápis não se alterou.
RESOLUÇÃO:
RESOLUÇÃO:
O buraco dilata-se como se estivesse totalmente preenchido pelo material
do disco metálico.
Resposta: C
4. (UFPB) – Ultimamente, o gás natural tem se tornado uma
importante e estratégica fonte de energia para indústrias. Um dos
modos mais econômicos de se fazer o transporte do gás natural de sua
origem até um mercado consumidor distante é através de navios,
denominados metaneiros. Nestes, o gás é liquefeito a uma temperatura
muito baixa, para facilitar o transporte. As cubas onde o gás liquefeito
é transportado são revestidas por um material de baixo coeficiente de
dilatação térmica, denominado invar, para evitar tensões devido às
variações de temperatura. Em um laboratório, as propriedades térmicas
do invar foram testadas, verificando a variação do comprimento (L) de
uma barra de invar para diferentes temperaturas (T). O resultado da
experiência é mostrado, a seguir, na forma de um gráfico:
Resposta: A
3. (IJSO) – A figura 1 mostra um disco metálico com um buraco no
centro.
Com base nesse gráfico, conclui-se que o coeficiente de dilatação
térmica linear da barra de invar é:
a) 1 · 10–6/°C
b) 2 · 10–6/°C
c) 5 · 10–6/°C
–6
–6
d) 10 · 10 /°C
e) 20 · 10 /°C
RESOLUÇÃO:
L = L0
1,0001m – 1,0m = 1,0m · · (50°C – 0°C)
0,0001
= ––––––
50°C
= 2,0 · 10–6°C–1 →
= 2,0 · 10–6°C
Resposta: B
Qual das figuras de 2 a 5 mostra esquematicamente a aparência do
disco após ser aquecido uniformemente?
a) Figura 2
b) Figura 3
c) Figura 4
d) Figura 5
– 73
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 74
MÓDULO 12
OS PRINCÍPIOS DA ÓPTICA GEOMÉTRICA
1. (FUVEST) – Uma determinada montagem óptica é composta por
um anteparo, uma máscara com furo triangular e três lâmpadas, L1, L2 e
L3, conforme a figura abaixo. L1 e L3 são pequenas lâmpadas de
lanternas e L2, uma lâmpada com filamento extenso e linear, mas
pequena nas outras dimensões. No esquema, apresenta-se a imagem
projetada no anteparo com apenas L1 acesa.
As figuras projetadas no anteparo por L1, L2 e L3 têm o formato esboçado
a seguir.
Resposta: D
O esboço que melhor representa o anteparo iluminado pelas três
lâmpadas acesas é:
RESOLUÇÃO:
A lâmpada L3 projeta no anteparo uma figura idêntica à projetada pela
lâmpada L1. Isso ocorre devido à simetria de L3 e L1 com relação ao
triângulo recortado na máscara central.
A lâmpada extensa L2, por sua vez, pode ser caracterizada como uma
associação de lâmpadas puntiformes dispostas verticalmente. Raciocinando
dessa forma, cada uma dessas pequenas lâmpadas projeta no anteparo uma
figura triangular. A reunião de todas essas figuras determina um
quadrilátero, como representado a seguir.
74 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 75
2. (FGV-SP) – O vendedor de churros havia escolhido um local
muito próximo a um poste de iluminação. Pendurado no interior do
carrinho, um lampião aceso melhorava as condições de iluminação.
3. (UCMG) – Num dia ensolarado, um aluno de 1,7m mede a sua
sombra, encontrando 1,2m. Se, naquele instante, a sombra de um poste
nas proximidades mede 4,8m, qual é a altura do poste?
a) 3,4m b) 4,3m c) 7,2m d) 6,8m e) 5,3m
RESOLUÇÃO:
Admitindo que o centro de todos os elementos da figura, exceto as finas
colunas que suportam o telhado do carrinho, estão no mesmo plano
vertical, considerando apenas as luzes emitidas diretamente do poste e
do lampião e, tratando-os como os extremos de uma única fonte
extensa de luz, a base do poste, a lixeira e o banquinho, nessa ordem,
estariam inseridos em regiões classificáveis como
a) luz, sombra e sombra.
b) luz, penumbra e sombra.
c) luz, penumbra e penumbra.
d) penumbra, sombra e sombra.
e) penumbra, penumbra e penumbra.
Como os raios de luz, provenientes do Sol, são considerados paralelos, os
triângulos ABC e A’B’C’ são semelhantes:
H
S
H
4,8
––– = ––– ⇒ ––– = ––– ⇒ H = 6,8m
h
s
1,7
1,2
Resposta: D
RESOLUÇÃO:
Observamos na figura que, à esquerda do ponto A, ocorre incidência de
luz de ambas as fontes, lâmpada e lampião, definindo uma região iluminada
que contém a base do poste. Entre os pontos A e B, não ocorre incidência
luminosa a partir de nenhuma das fontes, definindo assim uma região de
sombra na qual encontramos a lixeira e o banquinho, portanto temos, para
a base do poste, a lixeira e o banquinho, regiões de luz, sombra e sombra,
respectivamente.
Resposta: A
– 75
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 76
4. (VUNESP) – Em 3 de novembro de 1994, no período da manhã,
foi observado, numa faixa ao sul do Brasil, o último eclipse solar total
do milênio passado. Supondo retilínea a trajetória da luz, um eclipse
pode ser explicado pela participação de três cor pos alinhados:
um anteparo, uma fonte e um obstáculo.
a) Quais são os três corpos do Sistema Solar envolvidos nesse eclipse?
b) Desses três corpos, qual deles faz o papel de anteparo? De fonte? De
obstáculo?
2. (UFJF-MODELO ENEM) – De acordo com especialistas, para
que o olho humano possa distinguir dois objetos puntiformes situados
próximos um do outro, é preciso que a imagem de cada um deles se
forme na retina em cones separados por pelo menos um cone, como
ilustra a figura abaixo. Admita que a distância entre dois cones adjacentes seja igual a 1μm (= 10–6m) e a distância entre a córnea e a retina
seja de 2,5cm.
RESOLUÇÃO:
De acordo com isso, qual é a maior distância d em que é possível
distinguir objetos puntiformes separados por 1cm?
a) 25m
b) 125m
c) 10cm
d) 30m
e) 2,5m
RESOLUÇÃO:
d
1cm
Semelhança de triângulos: –––––– = –––––––––– ⇒ d = 12500cm
2,5cm
2 . 10–4cm
Da qual:
MÓDULO 13
OS PRINCÍPIOS DA ÓPTICA GEOMÉTRICA
1. (UNIRIO-RJ) – No mundo artístico as antigas “câmaras escuras”
voltaram à moda. Uma câmara escura é uma caixa fechada de paredes
opacas que possui um orifício em uma de suas faces. Na face oposta à
do orifício fica preso um filme fotográfico, onde se formam as imagens
dos objetos localizados no exterior da caixa, como mostra a figura.
Suponha que um objeto de 3m de altura esteja a uma distância de 5 m
do orifício, e que a distância entre as faces seja de 6 cm.
Calcule a altura h da imagem.
RESOLUÇÃO:
Os triângulos observados na figura são semelhantes, assim:
300
500
–––– = –––– ⇒
h
6
h = 3,6 cm
Observe que utilizamos o fato de a luz se propagar de forma retilínea em
meios ordinários.
76 –
Resposta: B
d = 125m
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 77
3. (FGV-SP-MODELO ENEM) – O professor pede aos grupos de estudo que apresentem à classe suas principais conclusões sobre os fundamentos para o desenvolvimento do estudo da óptica geométrica.
GRUPO I
GRUPO II
GRUPO III
GRUPO IV
4. (MODELO ENEM) – O uniforme da seleção brasileira de futebol
é composto de calção azul e camisa amarela.
Os feixes de luz podem apresentar-se em raios
paralelos, convergentes ou divergentes.
Os fenômenos de reflexão, refração e absorção ocorrem
isoladamente e nunca simultaneamente.
Enquanto num corpo pintado de preto fosco predomina
a absorção, em um corpo pintado de branco predomina
a difusão.
Os raios luminosos se propagam em linha reta nos
meios homogêneos e transparentes.
São corretas as conclusões dos grupos
a) I e III, apenas.
b) II e IV, apenas.
d) II, III e IV, apenas.
e) I, II, III e IV.
c) I, III e IV, apenas.
RESOLUÇÃO:
Grupo I – conclusão CORRETA.
Em um recinto escuro, iluminado apenas com luz amarela de sódio,
supondo que o uniforme seja constituído de pigmentos puros, ele
apresentar-se-á
a) inteiramente preto.
b) com calção e camisa amarelos.
c) com calção amarelo e camisa preta.
d) com calção preto e camisa amarela.
e) inteiramente branco.
RESOLUÇÃO:
Os feixes de luz podem ser cilíndricos, cônicos convergentes e cônicos divergentes, conforme indicam as figuras.
Grupo II – conclusão ERRADA.
Os fenômenos de reflexão, refração e absorção podem ocorrer em conjunto.
É o que acontece, por exemplo, quando a luz incide sobre a superfície da
água de uma piscina.
Grupo III – conclusão CORRETA.
Nos corpos de cores claras, predomina a reflexão difusa em detrimento da
absorção.
Grupo IV – conclusão CORRETA.
A frase citada é o princípio da propagação retilínea da Luz.
Resposta: C
Resposta: D
– 77
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 78
IMAGEM DE UM OBJETO,
ESPELHO PLANO E CAMPO VISUAL
2. (FUVEST-SP) – Um motorista de automóvel, ao olhar para o seu
retrovisor, vê um caminhão e lê, na imagem do para-choque, a palavra
SORRIA. Podemos concluir que no para-choque do caminhão estava
escrito:
a) SORRIA
b) SORRIA
c) AIRROS
d)
e)
AIRROS
1. (UPE) – A respeito dos espelhos planos, analise as afirmações a
seguir:
I. Nos espelhos planos, o ângulo de reflexão é igual ao ângulo de
incidência.
II. Para um espelho plano, pontos-objetos e pontos-imagens, têm-se
naturezas contrárias: se o objeto é real, a imagem é virtual e viceversa.
III.São formadas três imagens de um objeto, quando este é colocado
entre dois espelhos planos, que formam entre si um ângulo de 90°.
Está CORRETO o que se afirma em
a) I e II, apenas.
b) I e III, apenas.
d) I, apenas.
e) I e III, apenas.
360°
N = ––––– – 1 = 4 – 1
90°
N = 3 imagens
Resposta: C
RESOLUÇÃO:
A imagem é enantiomorfa ao objeto.
Resposta: C
c) I, II e III.
RESOLUÇÃO:
I. Correta.
De acordo com as leis da reflexão, os ângulos de incidência e de reflexão
são congruentes, além disso, o raio incidente, a reta normal e o raio
refletido são coplanares.
II. Correta.
Para um objeto real em frente à face refletiva do espelho plano, a
imagem é obtida pelo prolongamento de raios refletidos atrás do
espelho, caracterizando a imagem como virtual.
Para um objeto virtual, obtido com o auxílio de uma lente convergente,
por exemplo, a imagem será real.
III.Correta.
360°
N = ––––– – 1
3. (MODELO ENEM) – A figura a seguir representa esquematicamente um espelho plano que é transladado da posição E1 para a
posição E2 em relação ao objeto fixo AB.
A imagem desloca-se de A1B1 para A2B2. Para um deslocamento d do
objeto, o deslocamento da imagem será igual a:
d
d
e) –––
a) d
b) 2d
c) 4d
d) –––
2
4
RESOLUÇÃO:
Resposta: B
78 –
SORRIA
MÓDULO 14
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 79
MÓDULO 15
TRANSLAÇÃO E ROTAÇÃO DE UM ESPELHO
PLANO – ASSOCIAÇÃO DE ESPELHOS PLANOS
2. Considere uma pessoa e um espelho plano, movendo-se em
relação a um referencial ligado à superfície terrestre, com as velocidades escalares indicadas.
1. (AFA-RJ) – Um objeto A, fixo, está inicialmente a uma distância
de 2,5m de um espelho plano. O espelho é deslocado paralelamente à
sua posição inicial, afastando-se mais 0,5m do objeto A. Pode-se
afirmar que o deslocamento da imagem em relação ao objeto e a
distância da imagem ao espelho valem, respectivamente
a) 0,5m e 6,0m
b) 1,0m e 6,0m
c) 1,0m e 3,0m
d) 0,5m e 3,0m
e) 0,5m e 2,5m
RESOLUÇÃO:
Qual a velocidade da imagem da pessoa em relação à superfície terrestre?
RESOLUÇÃO:
Utilizando o método da superposição de efeitos, temos:
1) Se o espelho estivesse parado e apenas a pessoa se movesse com
velocidade escalar de 4,0m/s, a velocidade escalar da sua imagem seria
V1 = –4,0m/s.
1) Deslocamento da imagem em relação ao objeto: 1,0m
2) Distância da imagem ao espelho: 3,0m
Resposta: C
2) Se a pessoa estivesse parada e apenas o espelho se movesse com velocidade escalar de 5,0m/s, a velocidade escalar da imagem seria
V2 = 10m/s.
3) Superpondo os efeitos (1) e (2), a velocidade escalar da imagem em relação
à Terra será V = V1 + V2 = –4,0 + 10 = + 6,0m/s
Resposta: +6,0m/s
– 79
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 80
3. (UPF-RS) – Dois espelhos, como indicados na figura, estão
posicionados numa mesa e existe entre eles um objeto.
MÓDULO 16
RAIOS NOTÁVEIS E CONSTRUÇÃO
DE IMAGENS NOS ESPELHOS ESFÉRICOS
O maior ângulo entre os espelhos, para que se possam enxergar onze
imagens inteiras desse objeto, será de:
a) 20°
b) 30°
c) 45°
d) 60°
e) 120°
RESOLUÇÃO:
A fórmula é expressa por:
Nas questões de 1 a 6, o ponto F representa o foco principal do espelho
esférico, C o centro de curvatura e V o vértice. Obtenha, graficamente,
a posição da imagem do objeto AB. Classifique-a quanto à sua natureza
(real ou virtual), tamanho (maior, menor ou igual) e orientação (direita
ou invertida) em relação ao objeto.
1.
360°
N = –––– – 1
Para N = 11, temos:
360°
11 = –––– – 1
360°
12 = ––––
= 30°
Resposta: B
4. (FEI) – No esquema abaixo, há um espelho plano E, um objeto O,
sua imagem O’ e cinco observadores: 1, 2, 3, 4, 5.
real
invertida
maior
virtual
direita
menor
igual
RESOLUÇÃO:
Qual alternativa apresenta somente os observadores que enxergam o
objeto refletido no espelho?
a) 1, 2, 3, 4, 5.
b) 1, 2, 3
c) 3, 4, 5
d) 1, 2
e) 4, 5
RESOLUÇÃO:
Imagem real, invertida e menor.
Pela construção do campo visual do objeto em relação aos observadores,
concluímos que somente 1 e 2 enxergam o objeto refletido no espelho.
Resposta: D
80 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 81
RESOLUÇÃO:
2.
Imagem real, invertida e maior.
real
invertida
maior
virtual
direita
menor
igual
4.
RESOLUÇÃO:
Imagem real, invertida e igual.
RESOLUÇÃO:
3.
real
invertida
maior
virtual
direita
menor
Portanto, a imagem estará no infinito e será denominada imagem imprópria.
igual
– 81
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 82
5.
6.
real
invertida
maior
real
invertida
maior
virtual
direita
menor
virtual
direita
menor
igual
igual
RESOLUÇÃO:
RESOLUÇÃO:
Imagem virtual, direita e maior.
Imagem virtual, direita e menor.
82 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 83
MÓDULO 17
ESTUDO ANALÍTICO DOS ESPELHOS ESFÉRICOS
1. Um pequeno objeto foi colocado sobre o eixo principal de um
espelho esférico côncavo, que obedece às condições de Gauss,
conforme ilustra a figura abaixo. O raio da esfera, da qual foi retirada
a calota que constitui o espelho, mede 1,00m.
2. (UFTM-MG) – Um objeto luminoso de 2cm de altura é posicionado perpendicularmente sobre o eixo principal de um espelho esférico
côncavo cuja distância focal vale 10cm e está a 20cm deste. Sabendo-se
que o espelho satisfaz as condições de Gauss, as características da
imagem por ele formada são:
a) 2cm de altura, real e invertida em relação ao objeto.
b) 4cm de altura, real e invertida em relação ao objeto.
c) 6cm de altura, real e direita em relação ao objeto.
d) 2cm de altura, virtual e invertida em relação ao objeto.
e) 4cm de altura, virtual e direita em relação ao objeto.
RESOLUÇÃO:
1) Altura da imagem:
i
f
A = ––– = –––––
o
f–p
i
10
Assim: ––– = –––––––
2
10 – 20
2 . 10
i = ––––––
– 10
Nessas condições, a distância entre esse objeto e sua respectiva imagem
conjugada é de
a) 240 cm
b) 150 cm
c) 75 cm
d) 60 cm
e) 50 cm
i = – 2cm
2) O fato de i ser negativo indica que a imagem é invertida e, portanto,
real.
Resposta: A
RESOLUÇÃO:
1) f = R = 0,50m
–––
2
2) p = f + 10cm = 60cm
3)
1 + 1 = 1
–––
–––
–––
p
p’
f
1 + 1 = 1 ⇒ 1 = 1 – 1 = 6–5 = 1
–––
–––
–––
–––
–––
–––
––––
–––
60
p’
50
p’
50
60
300
300
p’ = 300cm
4)
d = p’ – p ⇒
d = 240cm
– 83
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 84
3. (UEPB-PB-MODELO ENEM) – Numa aula, utilizando experimentos com material de baixo custo, o professor de óptica tenta mostrar,
aos seus alunos, a formação de imagens num espelho esférico. Para
realizar a demonstração, ele utilizou a superfície externa e espelhada de
uma bola de árvore de natal, cujo raio vale 10cm e, usando uma vela
acesa como objeto real, colocou-a sobre o eixo principal e anotou
cuidadosamente os dados de suas observações sobre a imagem obtida.
Considerando este espelho como ideal e colocando uma vela de 12cm de
altura, num ponto que se encontra a 25cm do vértice do espelho,
conforme a figura, o professor mostrou que a imagem é
a) imprópria.
b) direta com altura de 2,0cm.
c) invertida com altura de 2,0cm.
d) invertida com altura de 12cm.
e) direta com altura de 12cm.
RESOLUÇÃO:
Nos espelhos esféricos convexos, as imagens de objetos reais são virtuais e
direitas.
Aplicando-se a relação do aumento linear, temos:
o = +12cm
i
–5
Assim: ––– = –––––––
12
–5 – 25
Resposta: B
84 –
1. (URCA) – Um raio luminoso que se propaga no ar, nAr = 1, incide
obliquamente sobre um meio transparente de índice de refração n,
fazendo um ângulo de 60° com a normal. Nessa situação, verifica-se que
o raio refletido é perpendicular ao raio refratado, como mostra a figura.
O índice de refração n do meio é igual a:
a) 1/ 2
b) 3
/2
c) 3
3/2
d) e) 2/2
RESOLUÇÃO:
(I) Sendo θ0 = 60° o ângulo de incidência, θ1 o ângulo de reflexão e θ2 o
ângulo de refração, tem-se que:
(O ângulo de reflexão é sempre igual ao ângulo de
incidência.)
(II) θ1 + 90° + θ2 = 180° ⇒ 60° + 90° + θ2 = 180°
Das informações retiradas do texto, temos:
R
f = ––– ⇒ f = –5cm (espelho convexo)
2
12
i = ––– ⇒
6
ÍNDICE DE REFRAÇÃO E LEIS DA REFRAÇÃO
θ1 = θ0 = 60°
i
f
A = ––– = –––––
o
f–p
p = +25cm
MÓDULO 18
i = +2,0cm
i
–5
1
⇒ ––– = –––– = –––
12
–30
6
θ2 = 30°
(III) Lei de Snell: n sen θ2 = nar sen θ0
1
3
n sen 30° = 1 sen 60° ⇒ n ––– = –––
2
2
Da qual:
Resposta: C
n = 3
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 85
2. (UNIP) – Na figura, representamos dois meios homogêneos e
transparentes, A e B, separados por uma fronteira plana, e um raio de
luz monocromática passando do meio A para o meio B.
3. (UERJ) – Um raio de luz vindo do ar, denominado meio A, incide
no ponto O da superfície de separação entre esse meio e o meio B, com
um ângulo de incidência igual a 7° (sen 7° 0,12).
No interior do meio B, o raio incide em um espelho côncavo E que
obedece às condições de Gauss, passando pelo foco principal F.
O centro de curvatura C do espelho, cuja distância focal é igual a 1,0m,
encontra-se a 1,0m da superfície de separação dos meios A e B.
Observe o esquema:
Sejam nA e nB os índices de refração absolutos dos meios A e B, respectivamente.
nA
Sendo ––– = 3, o valor de α é:
nB
a) 30°
b) 37°
c) 45°
RESOLUÇÃO:
Lei de Snell:
nA sen α = nB sen 2α
nA
––– sen α = 2 sen α cos α
nB
3
3 = 2 cos α ⇒ cos α = ––––
d) 53°
e) 60°
Considere os seguintes índices de refração:
nA = 1,0 (meio A)
nB = 1,2 (meio B)
Sabendo-se que para ângulos pequenos, até 10°, é razoável a aproximação tg α sen α, determine a que distância do ponto O o raio
emerge, após a reflexão no espelho.
RESOLUÇÃO:
O caminho óptico do raio luminoso até sua emergência do meio B está
esboçado na figura a seguir.
2
α = 30°
Resposta: A
(I) Lei de Snell:
nB sen r = nA sen i
1,2 sen r = 1,0 sen 7° ⇒ 1,2 sen r = 0,12
sen r = 0,10 ⇒
tg r 0,10
(II)No triângulo OPQ:
––––
––––
QO
QO
tg r = –––––
⇒ 0,10 = –––––
––––
3,0
PQ
––––
QO = 0,30m
Resposta: 0,30m
– 85
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 86
FRENTE 3 – ELETRICIDADE E MECÂNICA
MÓDULO 11
ENERGIA ELÉTRICA, POTÊNCIA ELÉTRICA
E POTÊNCIA DISSIPADA PELO RESISTOR
1. (UNESP) – Para iluminar determinado ambiente, o circuito a
seguir foi montado com duas lâmpadas, L1 e L2, de valores nominais
(120V – 100W) e (120V – 60W), respectivamente, com duas chaves
interruptoras, C1 e C2, ambas de resistência desprezível, e com fios de
ligação ideais. O circuito é alimentado por uma diferença de potencial
constante de 120V.
Com a chave C1 fechada e C2 aberta, o circuito dissipa 100 W. Com a
chave C1 aberta e C2 fechada, dissipa 60 W. Se as duas chaves forem
fechadas simultaneamente, o circuito dissipará, em W, uma potência
igual a
a) 320
b) 160
c) 120
d) 80
e) 40
RESOLUÇÃO:
Com as duas chaves fechadas, as lâmpadas estarão ligadas em paralelo com
a fonte e operando de acordo com seus dados nominais, assim:
2. (SIMULADO ENEM) – Nos chuveiros elétricos, transformamos
energia elétrica em energia térmica em virtude do Efeito Joule que
ocorre quando a corrente elétrica atravessa o resistor do chuveiro.
A temperatura da água está ligada à potência elétrica do chuveiro, que
vai depender da resistência elétrica de seu resistor.
Sendo U a tensão elétrica utilizada (110V ou 220V), I a intensidade da
corrente elétrica e R a resistência elétrica do resistor, a potência P é
dada pelas relações:
U2
P = UI = RI2 = –––
R
Uma chave seletora pode ocupar as posições A, B ou C indicadas na
figura, que correspondem, não respectivamente, às posições de morno,
quente ou muito quente para a temperatura desejada para o banho.
Escolhendo a equação adequada para o cálculo da potência P, assinale
a opção correta que faz a associação entre as posições A, B e C e a
temperatura desejada para a água.
a)
b)
c)
d)
e)
A – quente; B – morno; C – muito quente
A – quente; B – muito quente; C – morno
A – muito quente; B – morno; C – muito quente
A – morno; B – quente; C – muito quente
A – morno; B – muito quente; C – quente
Ptotal = P1 + P2
Ptotal = 100 + 60 (W)
Ptotal = 160W
Resposta: B
RESOLUÇÃO:
Em uma residência, a tensão elétrica U é mantida constante (no caso,
U2
220V); portanto, devemos usar a expressão P = ––– para analisar
R
como a potência P varia com a resistência R : P é inversamente proporcional
R
a R. Na posição B, temos Req = ––– (mínima), que corresponde à tempera2
tura muito quente. Na posição C, temos Req = 2R (máxima), que corresponde à temperatura menor: morno.
Resposta: B
86 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 87
3. (UNESP-2013) – Determinada massa de água deve ser aquecida
com o calor dissipado por uma associação de resistores ligada nos
pontos A e B do esquema mostrado na figura.
Para isso, dois resistores ôhmicos de mesma resistência R podem ser
associados e ligados aos pontos A e B. Uma ddp constante U, criada por
um gerador ideal entre os pontos A e B, é a mesma para ambas as
associações dos resistores, em série ou em paralelo.
Considere que todo calor dissipado pelos resistores seja absorvido pela
água e que, se os resistores forem associados em série, o aquecimento
pretendido será conseguido em 1 minuto. Dessa forma, se for utilizada
a associação em paralelo, o mesmo aquecimento será conseguido num
intervalo de tempo, em segundos, igual a
a) 30
b) 20
c) 10
d) 45
e) 15
RESOLUÇÃO:
O mesmo aquecimento, nas duas situações, implica:
εeᐉ
= εeᐉ
paralelo
série
Pp . Δtp = Ps . Δts
U2
U2
––– . Δtp = ––– . Δts
Rp
Rs
U2
U2
–––– . Δtp = –––– . Δts
R/2
2R
4. (VUNESP) – No circuito elétrico, submetido em seus terminais
a uma diferença de potencial constante de 100V, estão associados os
resistores R1, R2, R3 e R4, idênticos e iguais a 10.
a) Para que funções de leitura estão correta e respectivamente posicionados no circuito os multímetros P, Q e S?
b) Determine a potência no resistor R3, considerando os multímetros
P, Q e S ideais.
RESOLUÇÃO:
a) O multímetro P está corretamente posicionado para atuar como um
amperímetro efetuando a leitura da intensidade total de corrente elétrica
que percorre o circuito.
O multímetro Q está corretamente posicionado para atuar como um
amperímetro que fará a leitura da intensidade de corrente elétrica que
percorre o resistor R2.
O multímetro S está corretamente posicionado para atuar como um
voltímetro que fará a leitura da ddp no resistor R2.
E
100
b) itotal = ––––– = ––––––––––––– (A) = 4,0A
Req
10
10 + ––– + 10
2
itotal
4,0
i3 = ––––– = ––––– (A) = 2,0A
2
2
∴ P3 = R3 i32 = 10 . (2,0)2 (W) ⇒
P3 = 40W
Respostas: a) P e Q: amperímetros
S: voltímetro
b) 40W
Δts
Δtp = ––––
4
Sendo Δts = 1 minuto = 60s, temos:
60
Δtp = ––– (s)
4
Δtp = 15s
Resposta: E
– 87
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 88
MÓDULO 12
ENERGIA ELÉTRICA, POTÊNCIA ELÉTRICA
E POTÊNCIA DISSIPADA PELO RESISTOR
1. (VUNESP) – Um aquecedor elétrico (A), uma torradeira (T) de
750W e um grill (G) de 1000W são conectados em um circuito sob
tensão de 120V, como mostrado na figura.
2. (OPF) – Três lâmpadas possuem resistência de 0,5, 1,5 e
2 ohms, respectivamente. Se quisermos associá-las em um circuito
elétrico com uma fonte de tensão 8V, qual a energia mínima gasta por
esse sistema após 2 horas de funcionamento?
a) 1,15 . 105 J
b) 1,20 . 105 J
c) 1,30 . 105 J
d) 1,38 . 105 J
e) 1,46 . 105 J
RESOLUÇÃO:
Para uma tensão elétrica constante, a energia elétrica será mínima para
uma resistência elétrica máxima, assim:
Req = 0,50 + 1,5 + 2,0() = 4,0
A energia elétrica será dada por:
εeᐉ = P . Δt
εeᐉ =
Na figura, D representa um disjuntor que suporta até 25A, sem
desarmar. A potência máxima consumida no aquecedor elétrico deve
ser igual a
a) 4490W
b) 490W
c) 1250W
d) 125W
e) 3000W
RESOLUÇÃO:
Cálculo da potência elétrica máxima no trecho de circuito:
Pmáx = iimáx . Umáx
Pmáx = 25 . 120 (W)
Pmáx = 3000W
Assim:
Pmáx = Paquec + Ptorrad + Pgrill
3000 = Paquec + 750 + 1000
Paquec = 1250W
Resposta: C
88 –
εeᐉ =
εeᐉ
U2
––––– . Δt
Req
(8,0)2
––––– . 7200 (J)
4,0
 
W
s
1,15 . 105J
Resposta: A
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 89
3. (UNIFOR-CE) – Um aquecedor elétrico que fornece 840W é
utilizado para aquecer 600g de água, inicialmente à temperatura de
30°C. Supondo que todo o calor fornecido aqueça a água, a temperatura
por ela atingida após 1,0 minuto é, em °C,
Dados: cágua = 1,0cal/g ºC = 4,2J/g ºC
a) 35
b) 40
c) 45
d) 50
e) 55
4. (EFOMM-2013) – No circuito da figura, cada uma das duas lâmpadas incandescentes idênticas dissipava 36 W sob uma tensão inicial
V1 volts mantida pela bateria ε, r .
RESOLUÇÃO:
εel = Q
P Δt = m . c . Δθ
840 . 60 = 600 . 4,2 . Δθ
Δθ = 20ºC
∴ Δθ = θf – θi
20 = θf – 30
θf = 50ºC
Resposta: D
Quando, então, o filamento de uma delas se rompeu (anulando a corrente nessa lâmpada), observou-se que a tensão nas lâmpadas aumen4
tou para o valor V2 = –– V1 volts. Considerando as lâmpadas como
3
resistências ôhmicas, a potência na lâmpada que permaneceu acesa,
em watts, é:
a) 18
b) 32
c) 36
d) 64
e) 72
RESOLUÇÃO:
Potência dissipada num resistor:
V2
P = –––––
R
V2
R = –––––
P
Logo:
V12
V22
4
––––– = ––––– ⇒ P’1 = –––
P1
P’1
3
2
. 36 (W)
P’1 = 64W
Resposta: D
– 89
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 90
MÓDULO 13
2. (CESGRANRIO) – No circuito esquematizado abaixo, todas as
resistências são iguais a R.
PONTE DE WHEATSTONE
1.
Desafio interplanetário
Assim, a resistência equivalente entre os pontos A e B será igual a:
a) R/2
b) R
c) 2R
d) 4R
e) 5R
RESOLUÇÃO:
Estando a ponte em equilíbrio, o resistor situado entre C e D não é
percorrido por corrente e pode ser retirado do circuito.
No longínquo planeta Mongo, criaturas malignas sequestraram Dale
Arden, noiva do herói intergalático Flash Gordon. Na figura, Dale,
atada a um circuito, grita desesperada: help, help, help...
Flash sabe que se o gerador de plasma for acionado, a pobre Dale estará
literalmente frita, e pede conselho à princesa Azura.
Resposta: B
Seguindo a indicação, Flash pede ao Dr. Zarkov a caixa de resistores e
ruma para o cativeiro de Dale. Na caixa há cinco resistores de valores
nominais iguais a 2, 6, 11, 15 e 18 ohms. Quais deles Flash deve
escolher e como associá-los de modo a evitar que a formosa Dale
Arden passe por momentos difíceis?
RESOLUÇÃO:
Para que Dale Arden não seja eletrocutada, a ddp nos terminais em que
está ligada deve ser nula, ou seja, a Ponte de Wheatstone deve estar em
equilíbrio.
R . 5 = 2 . 60
R = 24Ω
Dessa maneira, devemos associar em série os resistores de 6Ω e 18Ω
(R = 6Ω + 18Ω = 24Ω).
90 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 91
3. No circuito da figura, L1 é o dobro de L2, sendo L1 e L2 partes do
mesmo fio homogêneo e de seção reta uniforme, e R2 é igual a
400 ohms.
4. (UEM) – A Ponte de Wheatstone é um circuito que permite a
comparação e a medida de resistências elétricas. A figura a seguir é
uma das formas usuais de se representar esse sistema. G simboliza o
galvanômetro, R as resistências, ε a fonte de corrente contínua.
Quando não passar corrente no galvanômetro G, o valor da resistência
x será
a) 200 ohms
b) 80 ohms
c) 800 ohms
d) 1200 ohms
e) 600 ohms
RESOLUÇÃO:
Observemos que as resistências elétricas dos trechos L1 e L2 serão diretaρᐉ
mente proporcionais aos seus comprimentos R = ––––– , assim:
A
R2 . L1 = x . L2
400 . (2L2) = x L2
x = 800Ω
Resposta: C
Considerando as informações do texto e da figura, assinale o que for
correto.
01) A Ponte de Wheatstone está em equilíbrio quando nenhuma
corrente passa pelo galvanômetro.
02) Na condição de equilíbrio, os resistores R1 e R2 estão associados
em série.
04) Se a corrente for igual a zero (i = 0) no galvanômetro, a diferença
de potencial entre os pontos C e D será zero (Vc – VD = 0).
08) Se a resistência R1 for desconhecida, seu valor poderá ser obtido
pela relação R1 = R3 (R2 / R4).
16) A Ponte de Wheatstone está em equilíbrio quando os valores dos
resistores satisfazem a igualdade R1R2 = R3R4.
RESOLUÇÃO:
01) VERDADEIRA.
Condição para o equilíbrio:
iGALV = 0
02) FALSA.
R1 e R3 estão associados em série na condição de equilíbrio, bem como
R2 e R4.
03) VERDADEIRA.
Se
iGALV = 0
, então VC – VD = 0
08) VERDADEIRA.
No equilíbrio: R1R4 = R3R2 ou R1 = R3 (R2/R4)
16) FALSA.
No equilíbrio: R1R4 = R3R2
– 91
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 92
MÓDULO 14
ESTÁTICA DO PONTO MATERIAL
1. (VUNESP-IFSP-MODELO ENEM) – O funcionário de uma
transportadora precisa montar um sistema de roldanas para elevar
verticalmente um objeto de peso P. Para isso, dispõe de três roldanas e
de fios, todos de massas desprezíveis. Com os materiais disponíveis,
pensou em montar os dois sistemas mostrados a seguir.
2. (UNESP-MODELO ENEM) – Em uma operação de resgate, um
helicóptero sobrevoa horizontalmente uma região levando pendurado
um recipiente de 200 kg com mantimentos e materiais de primeiros
socorros. O recipiente é transportado em movimento retilíneo e
→
→
uniforme, sujeito às forças peso ( P ), de resistência do ar horizontal (F)
→
e tração ( T), exercida pelo cabo inextensível que o prende ao helicóptero.
Sabendo-se que o ângulo entre o cabo e a vertical vale θ, que senθ = 0,6,
cosθ = 0,8 e g = 10 m/s2, a intensidade da força de resistência do ar que
atua sobre o recipiente vale, em N:
a) 500
b) 1 250
c) 1 500
d) 1 750
e) 2 000
RESOLUÇÃO:
No sistema indicado na figura 1, deveria exercer na extremidade livre
do fio uma força de intensidade F1 para manter o objeto de peso P
parado. Na montagem da figura 2, deveria exercer uma força de
intensidade F2 para equilibrar o mesmo objeto.
Analisando-se as figuras, pode-se afirmar corretamente que
a) F2 = F1.
b) F2 = 2F1.
c) F2 = 4F1.
d) F1 = 2F2.
e) F1 = 4F2.
RESOLUÇÃO:
Para o equilíbrio, a força resultante é nula e o polígono de forças é fechado.
Far
tg θ = –––
P
Far = P tg θ
Far = 2 000 . 0,6 (N)
–––
0,8
Far = 1 500N
Resposta: C
Portanto: 4F1 = 2F2 ⇒
Resposta: B
92 –
F2 = 2F1
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 93
3. (VUNESP-UEA-2013-MODELO ENEM) – Um estudante
construiu um modelo simplificado para explicar a ação de um cabo da
ponte estaiada Rio Negro.
MÓDULO 15
ESTÁTICA DO CORPO EXTENSO
1. (UFF-RJ) – Dois blocos de massas M1 = 6,0kg e M2 = 0,4kg
estão suspensos por fios de massas desprezíveis nas extremidades de
uma haste homogênea e horizontal. O conjunto está em equilíbrio
estático apoiado sobre um suporte em forma de cunha, como ilustrado
na figura.
No modelo, um cordão encontra-se preso ao centro de massa C da haste
horizontal que pesa 60N. Em uma de suas extremidades, a haste
horizontal, apoia-se na coluna.
Admitindo-se os valores sen 30º = 0,5 e cos 30º = 0,8, a intensidade da
força de tração do cordão conectado à coluna em N, é
a) 48
b) 60
c) 96
d) 120
e) 180
As marcas na haste indicam segmentos de mesmo comprimento.
a) Calcule a massa da haste.
b) Calcule a intensidade da força que o suporte exerce sobre a haste,
considerando-se a aceleração da gravidade local com módulo
g = 10m/s2.
RESOLUÇÃO:
RESOLUÇÃO:
a)
Para o equilíbrio da haste:
Ty = P
Para o equilíbrio da haste, o somatório dos torques, em relação ao
ponto O, deve ser nulo:
Tx = F
P1 d = P 2d + P2 5d
T cos 60° = P
1
T . ––– = 60
2
P1 = 2P + 5P2
T = 120N
M1 g = 2 Mg + 5 M2 g
M1 = 2M + 5M2
6,0 = 2M + 5 . 0,4
4,0 = 2M ⇒
M = 2,0kg
Resposta: D
b) Para que a força resultante na haste seja nula, devemos ter:
F = P1 + P2 + P
F = 60 + 4,0 + 20 (N) ⇒
F = 84N
Respostas: a) 2,0kg
b) 84N
– 93
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 94
2. (UERJ-2013) – Um homem de massa igual a 80kg está em
repouso e em equilíbrio sobre uma prancha rígida de 2,0m de comprimento, cuja massa é muito menor que a do homem.
A prancha está posicionada horizontalmente sobre dois apoios, A e B,
em suas extremidades, e o homem está a 0,2m da extremidade apoiada
em A.
A intensidade da força, em newtons, que a prancha exerce sobre o
apoio A equivale a:
a) 200
b) 360
c) 400
d) 720
Adote g = 10,0m/s2
3. (EFOMM-2013) – Uma viga metálica uniforme de massa 50kg
e 8,0m de comprimento repousa sobre dois apoios nos pontos B e C.
Duas forças verticais estão aplicadas nas extremidades A e D da viga:
→
→
a força F1 de módulo 20N para baixo e a força F2 de módulo 30N, para
cima, de acordo com a figura.
RESOLUÇÃO:
Se a viga se encontra em equilíbrio estável, o módulo, em newtons, da
reação FB no apoio B vale:
Dado: g = 10 m/s2
a) 795
b) 685
c) 295
d) 275
e) 195
O somatório dos torques, em relação ao ponto B, deve ser nulo:
PH . dP = NA . dA
RESOLUÇÃO:
800 . 1,8 = NA . 2,0
NA = 720N
Resposta: D
O somatório dos torques em relação ao ponto C, deve ser nulo:
FB . 4,0 = 3,0 . 2,0 + 500 . 2,0 + 20 . 6,0
4,0 FB = 60 + 1000 + 120 = 1180
FB = 295N
Resposta: C
94 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 95
4. (FUVEST-TRANSFERÊNCIA-2013) – A torre vertical de um
guindaste se enterra por uma profundidade f = 10,0m, conforme a
figura. O guindaste fica equilibrado quando a carga de 1,0 tonelada e
o contrapeso de massa mc estão às distâncias da torre central d = 10,0m
e ᐉ = 5,0m, respectivamente. Nessa condição, a componente horizontal
da força do chão na torre é nula, em todos os pontos.
MÓDULO 16
ÍMÃS, CAMPO MAGNÉTICO
E FORÇA MAGNÉTICA DE LORENTZ
1. (MODELO ENEM) – Nas figuras abaixo, estão desenhadas as
linhas de campo magnético (linhas de indução) de alguns ímãs ou
sistemas de dois ímãs. Verifique quais estão corretas.
Considere que o braço horizontal foi construído de modo a não
interferir no equilíbrio e, por isso, ignore sua influência.
A aceleração local da gravidade tem módulo g = 10 m/s2.
1 t = 1000kg
A carga é deslocada para uma posição a d’ = 15,0m da torre central
sem mover o contrapeso da posição ᐉ = 5,0m e o equilíbrio passa a ser
mantido por apenas duas forças do chão sobre a torre, nos pontos O e
C. Nessa nova situação, a componente horizontal da força do chão
sobre a torre do guindaste no ponto C tem módulo igual a
a) 5,0 . 103N
b) 1,0 . 104N
c) 1,5 . 104N
d) 2,0 . 105N
e) 2,5 . 105N
RESOLUÇÃO:
O somatório dos torques, em relação ao ponto O, deve ser nulo:
Pc . d’ = Pcp . ᐉ + F . f
Estão corretas:
a) apenas a figura 2.
c) apenas as figuras 1 e 2.
e) as figuras 1, 2 e 3.
b) apenas a figura 3.
d) apenas as figuras 2 e 3.
RESOLUÇÃO:
As linhas de campo “nascem” no norte e “morrem” no sul. Logo, estão
corretas as figuras 1 e 2, apenas.
Observação ao professor: as linhas de indução são fechadas. Elas penetram
no ímã e se fecham.
Resposta: C
1,0 . 103 . 10 . 15,0 = 2,0 . 103 . 10 . 5,0 + F . 10,0
15,0 . 104 = 10,0 . 104 + F . 10,0
F = 5,0 . 103N
Resposta: A
– 95
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 96
2. Uma partícula de carga positiva q é lançada com velocidade
→
vetorial V numa região onde existe um campo magnético uniforme
→
representado por B. Sabe-se que, na partícula, atuou uma força mag→
nética F transmitida pelo campo. Indique, nas situações (1) e (2), a
direção e o sentido da força.
4. (MODELO ENEM) – Duas partículas, (1) e (2), foram lançadas
→
num campo magnético uniforme B e, devido exclusivamente à força
magnética, saíram de sua trajetória, como mostra a figura a seguir.
RESOLUÇÃO:
Usando a regra da mão esquerda, concluímos que:
Podemos afirmar que:
a) q1 > 0 e q2 < 0
c) q1 < 0 e q2 < 0
e) q1 = 0 e q2 > 0
b) q1 > 0 e q2 > 0
d) q1 < 0 e q2 > 0
RESOLUÇÃO:
Em cada partícula, temos o seguinte esquema:
3. Quando uma carga elétrica negativa é lançada num campo magnético, a força magnética não obedece à regra da mão esquerda usada
anteriormente. Temos de inverter um dos três vetores. Nas duas figuras
abaixo, um elétron foi lançado no campo magnético.
Determine
a) na figura 1, o sentido da força magnética sobre o elétron;
→ → →
b) na figura 2, o sentido dos vetores F , B e V.
→
→
Observação: Em ambas as figuras, F1 e F2 são forças magnéticas.
Resposta: A
RESOLUÇÃO:
→
a) Na figura 1, você coloca a mão esquerda e inverte o sentido do vetor F
obtido.
b) Na figura 2, adotamos os mesmos procedimentos usados na questão 2:
→
aplicamos a regra da mão esquerda e invertemos o sentido da força F
obtida.
96 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 97
MÓDULO 17
MOVIMENTO DE UMA
PARTÍCULA ELETRIZADA EM UM
CAMPO MAGNÉTICO UNIFORME
1. Uma partícula eletrizada de massa m e carga elétrica q positiva é
→
lançada num campo magnético uniforme com velocidade vetorial V,
de direção perpendicular ao campo magnético. A partícula descreve
um movimento circular uniforme (MCU) cujo raio é R.
São dados:
m = 1,2 . 10–24kg
q = 3,2 . 10–19C
V = 6,4 . 104m/s
B = 2,0 . 102T
Determine o valor de R.
RESOLUÇÃO:
1,2 . 10–24 . 6,4 . 104
m.V
R = ––––– ⇒ R = ––––––––––––––––––
(m) ⇒
q.B
3,2 . 10–19 . 2,0 . 102
3. (UCS) – Dentro do tubo de imagem de um televisor, a corrente
elétrica, numa bobina, aplica sobre um elétron passante um campo
magnético de 5,00 x 10–4 T, de direção perpendicular à direção da velocidade do elétron, o qual recebe uma força magnética de 1,00 x 10–14N.
Qual o módulo da velocidade desse elétron? (Considere o módulo da
carga do elétron como 1,60 x 10–19 C.)
a) 3,34 x 103m/s
b) 1,60 x 105m/s c) 7,60 x 106m/s
d) 4,33 x 107m/s
e) 1,25 x 108m/s
RESOLUÇÃO:
.q. = e = 1,60 . 10–19C
B = 5,00 . 10–4T
F = 1,00 . 10–14N
Temos
F = Fmg = .q. . V . B
R = 1,2 . 10–3m
F
1,00 . 10–14
V = –––––– ⇒ V = ––––––––––––––––––––– (m/s)
.q. . B
1,60 . 10–19 . 5,00 . 10–4
V = 1,25 . 108m/s
Resposta: E
2. Retome a questão anterior e considere que a partícula tenha
realizado meia volta e tenha escapado da ação do campo magnético,
como nos mostra a figura.
Determine o intervalo de tempo entre a sua entrada no campo e sua
saída. Adote 3.
RESOLUÇÃO:
s = R (meia volta) = 3 . 1,2 . 10–3m = 3,6 . 10–3m
V = 6,4 . 102 m/s
s
s = V . t ⇒ t = –––
V
3,6 . 10–3
t = ––––––––
(s) ⇒ t = 5,6 . 10–6s
6,4 . 102
– 97
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 98
4. (MODELO ENEM) – As bússolas foram inventadas por volta
de 1300 d. C. No entanto, somente duzentos anos depois foram usadas
em navegação, coincidentemente quando Colombro descobriu as
Américas e Cabral, o Brasil. Na época, além da bússola, usavam-se as
estrelas como referencial. Uma bússola possui uma agulha magnética
em que uma das pontas é pintada e é denominada polo norte e a outra,
polo sul.
MÓDULO 18
CAMPO MAGNÉTICO GERADO
POR CONDUTOR RETILÍNEO
1. Temos um campo magnético uniforme representado pelas suas
linhas de indução. Em cada uma das figuras, mostra-se um fio retilíneo,
de comprimento infinito, imerso no campo.
a) Indique o sentido da força magnética em cada fio.
b) Determine o módulo da força magnética que atua em um pedaço
de 2,0m do fio da figura 3, sabendo que i = 10A e B = 2,0 . 10–5 T.
Analise cada afirmativa e responda se é verdadeira ou falsa:
I. A agulha magnética aponta para o norte geográfico.
II. A agulha magnética aponta para o norte magnético.
III. O polo norte geográfico e o magnético são praticamente coincidentes.
IV. A agulha magnética aponta para o sul magnético.
Observação: quando se diz a agulha aponta para um determinado local,
significa que o seu polo norte aponta para esse local.
RESOLUÇÃO:
A Terra é um ímã de “ponta cabeça”.
I. VERDADEIRA.
II. FALSA.
III.FALSA
IV. VERDADEIRA.
RESOLUÇÃO:
a) Basta usar a regra da mão esquerda:
fig. 2
Como o fio é paralelo ao campo, a força magnética é nula.
F = B . i . ᐉ . sen 0º
zero
→ →
F = 0
98 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 99
b) F = B . i . ᐉ
F = 2,0 . 10 –5 . 10 . 2,0 (N)
F = 4,0 . 10-4N
2. (FMTM) – Uma corrente elétrica i percorre uma barra metálica
→
que está imersa no campo magnético uniforme B , como está indicado
na figura. Observa-se que a barra sofre a ação de uma força magnética
horizontal, com sentido para a direita.
3. Na figura que se segue, temos um condutor em forma de L percorrido por uma corrente elétrica de intensidade i = 8,0A e imerso no
interior de um campo magnético uniforme B = 2,0 . 10–3T, perpendicular a esta página.
Os trechos OM e ON têm o mesmo comprimento: 12m. Determine
a) a direção, o sentido e a intensidade da força magnética em cada
trecho;
b) a intensidade da força resultante no condutor em L.
Note e adote:
Admita que a equação F = B . i . L . sen seja válida, ainda que o
condutor não tenha comprimento infinito.
RESOlUÇÃO:
a) Usando a regra da mão esquerda, obteremos:
Represente as linhas de força do campo magnético na região em que se
encontra a barra condutora.
RESOLUÇÃO:
Usando regra da mão esquerda.
A intensidade da força em cada trecho é:
F = B . i . L . sen 90° = B . i . L
F = 2, 0 . 10–3 . 8,0 . 12 (N) ⇒ F = 192 . 10–3N ⇒ F = 1, 92 . 10–1N
→
O campo magnético B tem direção perpendicular a esta folha e sentido do
→
papel para o leitor. Como o campo B é uniforme, a figura pedida é:
b) A intensidade da força resultante é:
Fres = F 2 ⇒ Fres = 1, 92 . 10–1 . 2 N⇒ Fres 2,7 . 10–1 N
Respostas: a) 1,92 . 10–1N ;
b) 2,7 . 10–1N ; direções e sentidos nas figuras.
– 99
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 100
4. (UNESP) – Um dos lados de uma espira retangular rígida com
massa m = 8,0g, na qual circula uma corrente I, é atado ao teto por dois
fios não condutores de comprimentos iguais. Sobre esse lado da espira,
medindo 20,0cm, atua um campo magnético uniforme de 0,05T,
perpendicular ao plano da espira. O sentido do campo magnético é
representado por uma seta vista por trás, penetrando o papel, conforme
é ilustrado na figura.
Considerando se g = 10,0 m/s2, o menor valor da corrente que anula
as trações nos fios é:
a) 8,0A
b) 7,0A
c) 6,0A
d) 5,0A
e) 4,0A
RESOLUÇÃO:
Para que tenhamos o anulamento das forças de tração nos fios, a força
magnética sobre o ramo do condutor imerso no campo deve equilibrar a
ação da força peso; assim:
→
→
| Fmag| = | P |
B.i.ᐉ sen θ = m g
B.i.ᐉ sen 90° = m g
0,05 . i . 0,20 . 1 = 8,0 . 10–3 . 10,0
i = 8,0A
Resposta: A
100 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 101
FRENTE 1
MÓDULO 11
VETORES
1. (VUNESP) – No ensino médio, as grandezas físicas costumam ser
classificadas em duas categorias. Na primeira categoria, estão as
grandezas definidas apenas por um número e uma unidade de medida;
as grandezas da segunda categoria requerem, além disso, o conhecimento de sua direção e de seu sentido.
a) Como são denominadas as duas categorias, na sequência apresentada?
b) Preencha corretamente as lacunas, indicando uma grandeza física
da área de mecânica e outra da área de eletricidade, para cada uma
dessas categorias.
área
1ª categoria
2ª categoria
mecânica
.......................
......................
eletricidade .......................
......................
2.
a)
b)
c)
d)
e)
(UELON–PR) – São grandezas vetoriais a
energia cinética e a corrente elétrica.
corrente elétrica e o campo elétrico.
força e o calor.
aceleração e o trabalho.
aceleração e o campo elétrico.
3. (FATEC) – Duas forças têm intensidades F1 = 10N e F2 = 15N.
→ →
→
O módulo da resultante R = F1 + F2 não pode ser:
a) 4N
b) 10N
c) 15N
d) 20N
e) 25N
4. Duas forças de intensidades F1 = 6,0N e F2 = 8,0N agem sobre um
corpo.
a) Determine o intervalo de valores que a intensidade da resultante
pode assumir.
b) Determine a intensidade da resultante quando as forças forem
perpendiculares.
5. (MED-VASSOURAS-MG) – Quatro forças, cujos módulos, direções e sentidos são indicados na figura, atuam sobre uma partícula.
A ação conjunta dessas forças é equivalente à de uma única força de
intensidade igual a:
a) 3,0N b) 5,0N
c) 7,0N
d) 15,0N
e) 21,0N
→
→
6. (ESAM-SP) – Duas forças constantes, F1 e F2, de intensidades
F1 = 6,0N e F2 = 8,0N formam, entre si, um ângulo de 60°.
→
→
Qual o valor aproximado da intensidade da resultante entre F1 e F2?
3
1
Dados: sen 60° = ––––– e cos 60° = –––
2
2
MÓDULO 12
MOVIMENTO CIRCULAR UNIFORME
1. (UFPE) – As rodas de uma bicicleta possuem raio igual a 0,50m e
giram com velocidade angular constante de módulo igual a 5,0 rad/s. Qual
a distância percorrida, em metros, por esta bicicleta num intervalo de
10 segundos?
2. (UCG-GOIÁS-modificado) – Considere um modelo atômico em
que um elétron descreve em torno do núcleo um movimento circular e
uniforme com velocidade de módulo igual a 2,0 . 106m/s e raio de
órbita igual a 5,0 . 10–11m.
Determine
a) o módulo da velocidade angular do elétron;
b) o período orbital do elétron (adote π = 3);
c) o módulo da aceleração do elétron.
3. Admita que o Sol descreve, em torno do centro de nossa galáxia,
uma órbita circular com movimento uniforme.
O raio desta órbita é de 3. 1020m e o módulo da velocidade de
translação é igual a 3 . 105m . s–1.
Admitindo-se π 3 e a duração do ano terrestre igual a 3 . 107s, calcule:
a) o módulo da aceleração associada ao movimento orbital do Sol;
b) o período de translação associado ao movimento orbital do Sol,
expresso em anos terrestres.
4. (FUVEST) – Uma cinta funciona solidária com duas polias de raios
r1 = 10cm e r2 = 50cm.
Supondo-se que a polia maior tenha uma frequência de rotação f2 igual
a 60 rpm:
a) qual a frequência de rotação f1 da polia menor?
b) qual o módulo da velocidade linear da cinta? Adote π = 3.
– 101
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 102
5. Na figura, temos um sistema formado por três polias, A, B e C, de
raios respectivamente iguais a RA = 10cm, RB = 20cm e RC = 15cm, que
giram conjuntamente, encostadas uma na outra e sem que haja escorregamento entre elas.
A polia A é a polia motriz que comanda as demais e gira no sentido
horário com rotação uniforme e frequência de 30 rpm.
Seja X o ponto de contato entre as polias A e B e Y um ponto da
periferia da polia C.
Determine, adotando-se π = 3:
a) os módulos das velocidades lineares dos pontos X e Y;
b) o sentido de rotação e a frequência de rotação da polia B;
c) o sentido de rotação e o período de rotação da polia C.
MÓDULO 13
BALÍSTICA
1. (FUVEST) – Um gato dá um pulo, atingindo uma altura de 1,25m e
caindo a uma distância de 1,50m do local do pulo. Despreze o efeito do ar
e adote g = 10m . s–2.
a) Calcule a componente vertical de sua velocidade inicial.
b) Calcule o módulo da velocidade horizontal do gato.
c) Qual o módulo da aceleração vetorial do gato no ponto mais alto de
sua trajetória.
2. (FUVEST) – Num dia ensolarado, com sol a pique, um jogador
chuta uma bola, que descreve uma parábola. O gráfico que melhor
representa o módulo da velocidade V da sombra da bola, projetada no
solo, em função do tempo t, é:
6. Considere uma pessoa P na superfície terrestre deslocando-se da lilinha do Equador para o Polo Norte.
Para cada latitude , a pessoa, parada em relação à superfície terrestre,
descreve para um referencial fixo no centro O da Terra, um movimento
uniforme com uma trajetória circular de raio r e centro C no eixo de
rotação da Terra (ver figura).
3. (FUVEST) – Uma pessoa sentada num trem, que se desloca numa
trajetória retilínea e horizontal a 20m/s, lança uma bola verticalmente
para cima e a pega de volta no mesmo nível do lançamento. A bola atinge
uma altura máxima de 0,8m em relação a este nível. Adotando-se
g = 10m/s2 e desprezando-se o efeito do ar, pedem-se:
a) os módulos da velocidade vetorial e da aceleração vetorial da bola,
em relação ao solo terrestre, quando ela atinge sua altura máxima.
b) o tempo durante o qual a bola permanece no ar.
4. (UNEB-BA) – Um projétil é lançado a partir do solo horizontal,
→
com velocidade inicial V0, que forma com o solo um ângulo tal que
3
1
sen = ––– e cos = ––––– .
2
2
Neste movimento circular uniforme, a velocidade vetorial da pessoa
tem módulo V e sua aceleração vetorial tem módulo a.
Assinale a opção que traduz o gráfico de a em função de V quando a
pessoa vai do Equador para um dos polos.
A aceleração da gravidade local tem módulo g = 10m/s2 e despreza-se
o efeito do ar.
→
O projétil atingirá uma altura máxima de 20m se o módulo de V0 for
igual a:
a) 10m/s
b) 20m/s
c) 40m/s
d) 80m/s
e) 100m/s
5. Um atleta olímpico, participando da prova de salto à distância,
→
abandona o solo com velocidade V0 de módulo 10m/s e inclinada, em
relação ao plano horizontal, de um ângulo tal que sen = 0,45 e
cos = 0,90. Considere g = 10m/s2 e despreze o efeito do ar. A marca
conseguida pelo atleta foi de:
a) 7,9m
b) 8,0m
c) 8,1m
d) 8,2m
e) 8,3m
6. (FUVEST) – Num jogo de vôlei, o jogador que está junto à rede
salta e “corta” uma bola levantada na direção vertical, no instante em
que ela atinge sua altura máxima, h = 3,2m.
102 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 103
Nessa “cortada”, a bola adquire uma velocidade de módulo V, na
direção paralela ao solo e perpendicular à rede, e cai exatamente na
linha de fundo da quadra.
A distância entre a linha de meio da quadra (projeção da rede) e a linha de fundo é d = 9,0m.
Adote g = 10m/s2 e despreze o efeito do ar.
Calcule
a) o tempo decorrido entre a cortada e a queda da bola na linha de
fundo.
b) o módulo V da velocidade que o jogador transmitiu à bola.
3. (CESGRANRIO) – Em um referencial inercial, um bloco de madeira está em equilíbrio sobre um plano inclinado, como mostra a
figura.
7. (AFA) – Um projétil é disparado, a partir do solo horizontal, com
→
velocidade V0 de módulo igual a 250m/s e inclinada de , em relação
à horizontal. Após um intervalo de tempo T1, o projétil colide com um
obstáculo que está a uma altura H acima do solo e a uma distância
horizontal de 5250m do ponto de disparo.
Despreze o efeito do ar, adote g = 10m/s2 e sen = cos = 0,7.
Assinale a opção que representa, corretamente, a força exercida pelo
plano sobre o bloco.
Os valores de T1 e H são dados por:
a) T1 = 30s e H = 750m
b) T1 = 20s e H = 4500m
c) T1 = 20s e H = 750m
d) T1 = 30s e H = 4500m
MÓDULO 14
4. O gráfico a seguir representa a intensidade da força resultante em
um corpo em função da intensidade de sua aceleração.
1.a E 2.a LEI DE NEWTON
1. (UNESP) – As estatísticas indicam que o uso do cinto de segurança
deve ser obrigatório para prevenir lesões mais graves em motoristas e
passageiros no caso de acidentes. Fisicamente, a função do cinto está
relacionada com a
a) Primeira Lei de Newton.
b) Lei de Snell.
c) Lei de Ampère.
d) Lei de Ohm.
e) Primeira Lei de Kepler.
2. (FEI) – Uma tora de 1,0t deve ser arrastada, com atrito, sobre uma
superfície por uma distância de 200m. Para realizar tal tarefa, um
homem utiliza um trator e prende a tora com um cabo de aço, conforme
indica a figura. O trator apresenta velocidade escalar constante igual a
18km/h e move-se em trajetória retilínea.
Calcule
a) a massa do corpo;
b) o módulo da aceleração do corpo quando a força resultante tiver
intensidade de 12,0N.
5. (FUVEST) – Um corpo de massa igual a 3,0 kg move-se, sem atrito, num plano horizontal, sob a ação de uma força horizontal constante
de intensidade 7,0N. No instante t0 sua velocidade é nula. No instante
t1 > t0, a velocidade escalar é 21,0m/s. Calcule Δt = t1 – t0.
a) 3,0s
b) 9,0s
c) 12,0s
d) 16,0s
e) 21,0s
6. Um carro tem massa de 5,0 . 102kg e percorre uma trajetória retilínea com sua posição (espaço) definida em função do tempo, pela
relação:
x = 20,0 + 3,0t2 (unidades do SI)
Sabendo-se que a tração no cabo tem intensidade de 12kN, a resultante
das forças que atuam sobre a tora tem intensidade igual a:
a) zero
b) 6,0kN
c) 8,0kN
d) 10,0kN
e) 12,0kN.
Calcule
a) a intensidade da aceleração do carro;
b) a intensidade da força resultante no carro.
– 103
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 104
MÓDULO 15
PESO DE UM CORPO E 3.a LEI DE NEWTON
1. (UNIP) – A tabela a seguir indica o valor aproximado da intensidade da aceleração da gravidade na superfície de alguns planetas que
compõem o nosso sistema solar.
Na Terra, um corpo A tem massa de 1,0kg e um corpo B tem massa de
2,5kg.
Planeta
g(m/s2)
Mercúrio
3,0
Vênus
8,0
Terra
10
Marte
4,0
Júpiter
25
Saturno
10
Urano
8,0
Netuno
11
Assinale a opção correta:
a) O corpo A terá peso igual ao do corpo B nos planetas Vênus e
Urano.
b) Somente em Saturno a massa do corpo A continua sendo igual a
1,0kg.
c) A massa do corpo A é máxima em Júpiter.
d) O peso do corpo A é o mesmo em todos os planetas.
e) O peso do corpo B em Marte é igual ao peso do corpo A na Terra.
2. (FUVEST) – Um homem tenta levantar uma caixa de 5,0kg, que
está sobre uma mesa, aplicando uma força vertical de intensidade 10N.
Enquanto o sistema estiver caindo e desprezando-se a resistência do
ar, podemos afirmar que a tensão na corda vale:
a) zero
b) 2,0N
c) 10,0N
d) 20,0N
e) 30,0N
4. (UNITAU) – Assinale a alternativa correta:
a) As forças de ação e reação estão aplicadas em corpos distintos e, por
isso, não se equilibram.
b) As forças de ação e reação se equilibram.
c) As forças de ação e reação têm mesma direção, mesmo sentido e
mesma intensidade.
d) As forças de ação e reação estão aplicadas ao mesmo corpo.
e) As forças de ação e reação são iguais.
5. (UNESP) – Em 1992, comemorou-se os 350 anos do nascimento de
Isaac Newton, autor de marcantes contribuições à ciência moderna.
Uma delas foi a lei da gravitação universal. Há quem diga que, para
isso, Newton se inspirou na queda de uma maçã.
Suponha que F1 seja a intensidade da força exercida pela Terra sobre
a maçã e F2 a intensidade da força exercida pela maçã sobre a Terra.
Então
a) F1 será muito maior que F2.
b) F1 será um pouco maior que F2.
c) F1 será igual a F2.
d) F1 será um pouco menor que F2.
e) F1 será muito menor que F2.
→
6. Uma pessoa aplica, com a palma de sua mão, uma força F vertical
para cima de intensidade 12N em um livro de massa 1,0kg, num local
onde a aceleração da gravidade é constante e de intensidade igual a
→
→
10 m/s2. O livro fica sob a ação exclusiva da força F e de seu peso P.
a) Descreva (intensidade, direção e sentido) a força que o livro exerce
na mão da pessoa.
→
b) Descreva a reação à força P.
Nesta situação, a intensidade da força que a mesa aplica na caixa é:
a) 0N
b) 5N c) 10N
d) 40N
e) 50N
3. (FUVEST) – Uma pessoa segura uma esfera A de 1,0kg que está
presa numa corda inextensível C de 200g, a qual, por sua vez, tem presa
na outra extremidade uma esfera B de 3,0kg, como se vê na figura. A
pessoa solta a esfera A.
MÓDULO 16
APLICAÇÕES DAS LEIS DE NEWTON
1. (FUVEST) – A figura mostra dois blocos, A e B, empurrados por
uma força horizontal, constante, de intensidade F = 6,0N, em um plano horizontal sem atrito.
O bloco A tem massa de 2,0kg e o bloco B tem massa de 1,0kg.
a) Qual o módulo da aceleração do conjunto?
b) Qual a intensidade da força resultante sobre o bloco A?
104 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 105
2. No esquema, temos três blocos, A, B e C, em um plano horizontal
→
sem atrito sendo acelerados por uma força horizontal constante F, de
intensidade 14,0N. Não se considera o efeito do ar. As massas dos
blocos A, B e C são, respectivamente, iguais a 4,0kg, 2,0kg e 1,0kg.
6. (UFPE) – Um bloco de massa m1 = 1,0kg repousa sobre um segun→
do bloco de massa m2 = 2,0kg. Se uma força horizontal F é aplicada
sobre o segundo bloco, de tal forma a imprimir uma aceleração de
módulo a = 1,0 m/s2 ao conjunto, qual deve ser a intensidade da força de
atrito atuando entre os blocos para que um não escorregue sobre o outro?
O módulo da aceleração do sistema (a), a intensidade da força de
contato entre A e B (FAB) e a intensidade da força de contato entre B e
C (FBC) são dados por:
a(m/s2)
FAB(N)
FBC(N)
a)
2,0
12,0
6,0
b)
3,5
10,5
3,5
c)
2,0
6,0
2,0
d)
2,0
4,0
6,0
e)
2,0
4,0
2,0
3. (UFES) – A figura mostra três blocos de massas m1 = 15kg,
m2 = 25kg e m3 = 10kg, interligados por fios leves e inextensíveis. O
atrito entre os blocos e a superfície horizontal é desprezível.
MÓDULO 17
APLICAÇÕES DAS LEIS DE NEWTON
1. (FUND. CARLOS CHAGAS) – As trações dos fios f1 e f2, de
massas desprezíveis, são responsáveis pelo movimento vertical dos
corpos de massas 1,0kg (A) e 2,0kg (B), conforme mostra figura ao
abaixo.
Se o bloco de massa m3 é tracionado por uma força de módulo T = 20
→
N, o módulo da força horizontal F indicada é:
a) 20N
b) 40N
c) 60N
d) 80N
e) 100N
4. A figura representa o conjunto de dois blocos, A e B, de massas,
respectivamente, mA = 6,0kg e mB = 5,0kg que deslizam sem atrito sobre
uma superfície horizontal, sob ação de uma força constante e de
intensidade F. O dinamômetro ideal D indica 20,0N.
a) Calcule a intensidade da aceleração dos blocos;
b) Calcule o valor de F.
5. Os blocos A e B de massas respectivamente iguais a 5,0kg e 3,0kg
movem-se juntos sobre uma superfície horizontal e sem atrito com
aceleração de módulo igual a 2,0m/s2, conforme esquema abaixo:
Adote g = 10m/s2 e despreze o efeito do ar. Sabendo-se que os corpos
sobem com aceleração de intensidade a = 2,0m/s2, dirigida para cima,
calcule
a) a intensidade da força tensora no fio f1.
b) a intensidade da força tensora no fio f2.
2. (ITA) – O equipamento denominado trilho de ar ou “air track” tornou-se um dos meios mais adequados para se estudar movimentos
retilíneos sem atrito. A minimização do atrito entre um bloco e o trilho
se consegue injetando ar no interior do trilho, que sai através dos
orifícios na parte superior do trilho, formando um “colchão de ar” entre
o trilho e o bloco.
No mesmo trilho de ar (sem atrito), monta-se o arranjo da figura.
→
Sendo a intensidade de F1 igual a 50N, calcule
→
a) a intensidade de F2;
b) a intensidade da força de contato trocada entre A e B.
O bloco A tem massa mA = 3,0 . 10–1kg e o bloco B tem massa
mB = 2,0 . 10–1kg.
– 105
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 106
Admitindo-se que a aceleração da gravidade local tem módulo igual a
10 m . s–2 e que o fio é inextensível e sem peso, pedem-se:
a) a intensidade da aceleração dos blocos;
b) a intensidade da força que traciona o fio.
6. (VUNESP) – Considere o esquema adiante e despreze o atrito.
Determinar a intensidade da aceleração do sistema, a intensidade da
força aplicada pelo corpo B sobre A e a intensidade da força que
traciona a corda. Adote g = 10m/s2.
Dados: mA = 15,0kg; mB = 5,0kg; mC = 20,0kg
3. No esquema, o fio é ideal e desprezam-se quaisquer forças resistentes, bem como a inércia da polia.
O bloco A tem massa M, o bloco B tem massa m e o módulo da aceleração da gravidade é g.
a) Esquematize todas as forças em cada um dos blocos.
b) Escreva o princípio fundamental da dinâmica (2ª Lei de Newton),
para cada um dos blocos e para o sistema (A + B).
c) Calcule o módulo da aceleração do sistema.
d) Calcule a intensidade da força que traciona o fio.
MÓDULO 18
APLICAÇÕES DAS LEIS DE NEWTON
1. (UESPI) – O peso do bloco P é igual a 2,0N, mas o dinamômetro
suspenso no teto do elevador marca 2,5N.
4. No esquema da figura, o bloco A desliza em um plano horizontal
sem atrito. Não se considera o efeito do ar e o fio e a polia são ideais.
Os blocos A e B têm massas respectivamente iguais a M e m, com
M > m.
Sejam a e T os módulos da aceleração dos blocos e da força que
traciona o fio, respectivamente.
Se invertermos as posições de A e B, então
a) os valores a e T não se alteram.
b) os valores de a e T aumentam.
c) o valor de a aumenta e o valor de T diminui.
d) o valor de a diminui e o valor de T não se altera.
e) o valor de a aumenta e o valor de T não se altera.
5. (UNESP) – Nas duas situações mostradas nas figuras, carrinhos,
mesas, roldanas e fios são idênticos. Observa-se, porém, que, puxando
→
→
o fio (figura 2) com uma força F igual ao peso P do corpo dependurado
(figura 1), a aceleração do segundo carrinho é maior.
Com base na Segunda Lei de Newton, justifique o fato observado.
106 –
Concluímos que o elevador pode estar
a) em repouso;
b) subindo com velocidade constante;
c) subindo e diminuindo o módulo da velocidade;
d) descendo e aumentando o módulo da velocidade;
e) descendo e diminuindo o módulo da velocidade.
2. (UFPE) – Um objeto de massa igual a 2,0 kg tem seu peso medi
do com um dinamômetro suspenso do teto de um elevador, conforme
mostra a figura.
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 107
O dinamômetro está indicando 16N. Sendo g = 10m/s2, responda aos
quesitos que se seguem:
a) Qual o módulo e o sentido da aceleração do elevador?
b) O elevador está subindo ou descendo? Justifique sua resposta.
5. Dois blocos, A e B, de massas mA = 3,0kg e mB = 2,0kg estão
unidos por um fio ideal (sem peso e inextensível) que passa por uma
polia pendurada em um dinamômetro.
3. Um homem sobe numa balança no interior de um elevador. Com o
elevador parado, a indicação da balança é 60kg.
Se o elevador estiver subindo com movimento retardado e aceleração
de módulo igual a 2,0m/s2, qual será a indicação da balança?
(Considere g = 10m/s2.)
a) 48kg
b) 60kg
c) 72kg
d) 84kg
e) 96kg
4. Uma pessoa sustenta na mão um livro de massa 2,0kg a uma altura de 1,0m do chão no interior de um elevador, que está subindo verticalmente, com movimento retardado e aceleração de módulo 8,0m/s2.
A aceleração da gravidade local tem módulo igual a 10,0m/s2.
a) Qual a intensidade da força de ação e reação trocada entre a mão da
pessoa e o livro?
b) Se a pessoa abandonar o livro, qual o tempo de queda até o chão do
elevador?
Desprezam-se o atrito no eixo da polia, o efeito do ar e a massa da
polia.
Sendo g = 10m . s–2, pedem-se:
a) o módulo da aceleração dos blocos;
b) a intensidade da força tensora no fio;
c) a indicação do dinamômetro.
6. (UESPI) – É dada uma polia de inércia desprezível e sem atrito no
eixo. Por essa polia passa um fio muito leve, flexível e inextensível,
suportando em suas extremidades dois sólidos cujas massas são m1 =
20kg e m2 = 12kg, conforme é mostrado na figura. Inicialmente, fio
tenso, os sólidos repousam sobre o piso horizontal. É dado g = 10m/s2.
A partir de um dado instante, aplica-se ao eixo da polia uma força
constante de intensidade F = 600N, dirigida verticalmente para cima.
Então, as acelerações a1 e a2 dos corpos suspensos têm módulos, respectivamente, iguais a
a) 5m/s2 e 15m/s2.
b) 10m/s2 e 10m/s2.
c) 5m/s2 e 10m/s2.
d) 15m/s2 e 25m/s2.
e) zero e 5m/s2.
– 107
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 108
FRENTE 2
MÓDULO 11
6. (MACKENZIE-SP) – Uma barra metálica, ao variar sua
temperatura de 80°C, aumenta seu comprimento de 0,16%. O
coeficiente de dilatação volumétrica do material dessa barra é:
a) 6 . 10–5 °C–1
b) 5 . 10–5 °C–1
c) 4 . 10–5 °C–1
d) 3 . 10–5 °C–1
e) 2 . 10–5 °C–1
DILATAÇÃO TÉRMICA
DOS SÓLIDOS E DOS LÍQUIDOS
MÓDULO 12
1. (FUVEST-SP) – Café fervente é despejado em um copo de vidro.
O copo parte-se. Uma possível explicação seria:
a) A dilatação das várias partes do copo não é uniforme.
b) O ponto de fusão do vidro é próximo ao de ebulição do café.
c) Sendo o vidro transparente, o calor passa através dele com
facilidade.
d) A capacidade térmica do vidro é menor que a do café.
e) O calor específico do vidro é menor que o do café.
2. (FATEC) – Um fio de cobre de 100m sofre aumento de temperatura
de 10°C. O coeficiente de dilatação linear do cobre é
17 . 10–6 °C–1. A variação do comprimento foi de:
a) 17mm
b) 17cm
c) 17m
d) 1,7m
e) 100,17m
PRINCÍPIO DA ÓPTICA GEOMÉTRICA
1. (ITA) – Dos objetos citados a seguir, assinale aquele que seria
visível em uma sala perfeitamente escura:
a) um espelho;
b) qualquer superfície de cor clara;
c) um fio aquecido ao rubro; d) uma lâmpada desligada;
e) um gato preto.
2. (UEM) – Na figura, a câmara escura inverte a imagem do objeto.
3. (UNITAU) – Uma barra de material com coeficiente de dilatação
igual a 0,000024°C–1 foi aquecida de 37°C até 487°C. O comprimento
inicial era de 10m. A barra sofreu um aumento
a) de quase 11cm.
b) impossível de calcular.
c) de quase 3mm.
d) de pressão e de temperatura.
e) de aproximadamente 0,5mm.
4. (FUND. CARLOS CHAGAS) – Uma lâmina bimetálica de cobre
( = 14 . 10–6 °C–1) e de alumínio ( = 24 . 10–6 °C–1), soldados um no
outro, acha-se engastada numa parede, conforme a figura.
Isto se deve
a) ao princípio da reversibilidade dos raios de luz;
b) ao princípio da propagação retilínea dos raios de luz;
c) a uma ilusão de óptica;
d) ao princípio da refração da luz;
e) nenhuma das respostas anteriores.
3. Um objeto linear, de tamanho o = 10cm, está a 5,0cm de distância
de uma câmara escura de orifício de profundidade 20cm. Qual o
tamanho da imagem projetada?
Na temperatura t0°C, ela é retilínea. Levada a uma temperatura t°C,
a) a lâmina se curva para cima se t > t 0 e para baixo se t < t 0
b) a lâmina se curva para cima se t < t 0 e para baixo se t > t 0
c) a lâmina se curva para cima seja t > t 0 ou t < t 0
d) a lâmina se curva para baixo seja t > t 0 ou t < t 0
5. (PUCC) – Um pino metálico, a uma dada temperatura, ajusta-se
perfeitamente no orifício de uma placa metálica.
Se somente a placa for aquecida, verifica-se que
a) haverá contração apenas no orifício da placa.
b) haverá contração do pino e da placa.
c) o pino não mais passará pelo orifício.
d) o pino passará mais facilmente pelo orifício.
e) n.d.a.
108 –
4. (MACKENZIE) – A altura da imagem de um objeto fornecida
por uma câmara escura de orifício é diminuída quando
a) aumentamos o diâmetro do orifício;
b) diminuímos o diâmetro do orifício;
c) afastamos a câmara do objeto;
d) aproximamos a câmara do objeto;
e) aumentamos o comprimento da câmara.
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 109
MÓDULO 13
PRINCÍPIO DA ÓPTICA GEOMÉTRICA
2. (FUND. CARLOS CHAGAS) – Na figura abaixo, O é um
observador, E é um espelho plano e B é uma bola. I1, I2, I3, I4 e I5 são
pontos em um dos quais está localizada a imagem da bola conjugada
pelo espelho.
1. (FESP) – Um edifício projeta no solo uma sombra de 40m. No
mesmo instante, um observador toma uma haste vertical de 20cm e
nota que sua sombra mede 0,80m. A altura do edifício é de:
a) 4,0m
b) 8,0m
c) 10m
d) 20m
e) 40m
2. (PUCC) – Um observador nota que um edifício projeta no solo uma
sombra de 30m de comprimento, no instante em que um muro de 1,5m
de altura projeta uma sombra de 50cm. Determine a altura do edifício.
3. (U.E.ES) – Numa sala escura para revelação de fotografias, acendese uma lâmpada vermelha. Indique a cor que tomará um objeto
normalmente azul:
a) branco
b) azul
c) vermelho
d) preto
e) laranja
Em que ponto está localizada a imagem da bola?
a) I1
b) I2
c) I3
d) I4
4. (SANTA CASA) – Uma bandeira brasileira, tingida com pigmentos puros e iluminada com luz azul monocromática, é vista nas cores:
a) verde, amarela, azul e branca;
b) verde, amarela e branca;
c) azul e branca;
d) azul e preta;
e) totalmente azul.
3. (UF-JUIZ DE FORA) – Coloca-se a ponta de um lápis apoiada
em um espelho plano fixo de 2,0mm de espessura. A distância entre a
ponta do lápis e a sua imagem será de:
a) 10mm
b) 20mm c) 1,0mm d) 2,0mm e) 4,0mm
5. (PUC) – Num eclipse total da Lua, a posição relativa dos três astros,
Sol, Lua e Terra, é a seguinte:
a) o Sol entre a Lua e a Terra;
b) a Lua entre o Sol e a Terra;
c) a Lua e a Terra à esquerda do Sol; d) a Terra entre o Sol e a Lua.
e) I5
4. (SANTA CASA) – A figura que representa corretamente a
formação da imagem I do objeto O, sendo E um espelho plano, é:
MÓDULO 14
IMAGEM DE UM OBJETO,
ESPELHO PLANO E CAMPO VISUAL
1. (FUVEST-SP) – Maria e Joana são gêmeas e têm a mesma altura.
Maria está olhando-se num espelho vertical e encontra-se a 5,0m deste.
O espelho é retirado e Maria vê Joana na mesma posição e com as
mesmas dimensões com que via sua própria imagem. A distância d entre
Maria e Joana, nestas condições, é de:
a) 5,0m
b) 7,5m
c) 10m
d) 15m
e) 20m
– 109
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 110
5. (UNIP) – Na figura, temos um objeto real AB e um espelho plano
E.
MÓDULO 15
TRANSLAÇÃO E ROTAÇÃO DE UM ESPELHO
PLANO – ASSOCIAÇÃO DE ESPELHOS PLANOS
1. Um espelho plano fornece uma imagem de um objeto situado a uma
distância de 20cm do espelho. Afastando-se o espelho 30cm em uma
direção normal ao seu plano, que distância separará a antiga da nova
imagem?
A imagem de AB fornecida pelo espelho plano E tem aspecto mais
bem representado por:
2. Um objeto afasta-se de um espelho plano fixo, perpendicularmente
a este e com velocidade de módulo 5,0m/s. Determine o módulo da
velocidade da imagem do objeto
a) em relação ao espelho;
b) em relação ao objeto.
3. (FUVEST-SP) – A figura mostra uma vista superior de dois espelhos
planos montados verticalmente, um perpendicular ao outro. Sobre o
espelho OA, incide um raio de luz horizontal, no plano do papel,
mostrado na figura.
6. Um fotógrafo e uma garota estão alinhados numa mesma perpendicular a um espelho plano, conforme mostra o esquema:
Após reflexão nos dois espelhos, o raio emerge formando um ângulo
com a normal ao espelho OB.
O ângulo vale:
a) 0°
b) 10°
c) 20°
d) 30° e) 40°
A distância do fotógrafo à garota é d e a distância desta ao espelho é d/2.
Para que distância o fotógrafo deve focalizar sua máquina, se quiser
uma foto da imagem da garota dada pelo espelho?
4. (MACKENZIE) – Na figura a seguir, E1 e E2 são dois espelhos
planos dispostos perpendicularmente entre si. Os pontos objetos reais
A, B, C, D e E sofrem reflexões simultâneas nos dois espelhos.
7. (FUVEST-SP) – Um motorista de automóvel, ao olhar para o seu retrovisor, vê um caminhão e lê, na imagem do pára-choque, a palavra SORRIA.
Podemos concluir que no pára-choque do caminhão estava escrito:
b) S ORRIA
e)
c) AI RROS
SORRIA
a) S ORRIA
SO
IA
d)
RR
8. (CESGRANRIO) – Daniela, uma linda menininha de oito anos,
ficou completamente desconcertada quando, ao chegar em frente ao
espelho do seu armário, vestindo uma blusa na qual havia seu nome
escrito, viu a seguinte imagem do seu nome:
LE N D
a) DANI E LA b) A LE I N AD c)
d) AL E I NAD e) DAN IELA
A I
A
110 –
O ponto P indicado refere-se a uma das imagens do objeto:
a) A
b) B
c) C
d) D
e) E
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 111
5. (FUVEST-SP) – A figura F indica um ladrilho colocado perpendicularmente a dois espelhos que formam um ângulo reto. Assinale
a alternativa que corresponde às três imagens formadas pelos espelhos.
3. (UC-MG) – Um objeto real, colocado em frente de um espelho
convexo, possui imagem
a) real, invertida e maior do que o objeto.
b) real, invertida e menor do que o objeto.
c) virtual, direita e maior do que o objeto.
d) virtual, direita e menor do que o objeto.
e) real ou virtual, dependendo de sua posição.
4. Determine a imagem do ponto luminoso P, colocado diante de
espelhos esféricos, nos casos a seguir:
MÓDULO 16
RAIOS NOTÁVEIS E CONSTRUÇÃO
DE IMAGENS NOS ESPELHOS ESFÉRICOS
Nas questões 1 e 2, determine graficamente a imagem do objeto AB.
1.
5. (OSEC) – Um objeto AB, linear e frontal, é colocado no centro de
curvatura de um espelho côncavo. A imagem conjugada será
a) real, direita e ampliada.
b) real, invertida e reduzida.
c) virtual, direita e de mesmo tamanho do objeto.
d) virtual, invertida e ampliada.
e) real, invertida e de mesmo tamanho do objeto.
real
virtual
invertida
direita
maior
menor
igual
invertida
direita
maior
menor
igual
6. (MED. JUNDlAÍ) – A figura a seguir representa um objeto O,
colocado defronte a um espelho côncavo. C é o centro de curvatura e
F, o foco do espelho.
2.
real
virtual
Dê as características da imagem formada.
– 111
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 112
MÓDULO 17
MÓDULO 18
ESTUDO ANALÍTICO DOS ESPELHOS ESFÉRICOS
ÍNDICE DE REFRAÇÃO E LEIS DA REFRAÇÃO
1. (F. ESTÁCIO DE SÁ) – Um espelho esférico convexo tem raio
igual a 60cm. Colocamos uma seta luminosa a 30cm do vértice do
espelho. Observamos que a imagem tem as seguintes características:
a) está distante do espelho 15cm e é virtual;
b) está distante do espelho 15cm e é real;
c) está distante do espelho 10cm e é virtual;
d) está distante do vértice 30cm e é real;
e) não há formação de imagem neste caso.
1. (ITA) – O módulo da velocidade da luz na água é igual a 3/4 do
módulo da velocidade da luz no vácuo.
Qual o índice de refração absoluto da água?
2. (FUND. CARLOS CHAGAS) – Um espelho esférico côncavo é
utilizado para projetar, sobre uma tela, a imagem do Sol. A distância
focal do espelho é 2,0 metros. Qual é, aproximadamente, a distância
entre a imagem do Sol e o espelho?
3. (MACKENZIE) – Um homem de altura H está em pé, em frente
a um espelho esférico côncavo, de distância focal f, a uma distância x
do vértice do espelho. Para que o espelho conjugue uma imagem real
H
do homem, de altura –– , qual deve ser o valor de x?
3
4. (MACKENZIE) – Mediante um espelho localizado a 1,80m de um
objeto luminoso frontal, deseja-se obter uma imagem direita, cuja
grandeza seja 2/3 da do objeto. Qual o tipo de espelho a adotar e sua
distância focal?
2. (FUND. CARLOS CHAGAS) – O índice de refração do vidro em
relação ao vácuo vale 1,50. O módulo da velocidade da luz no vácuo é
de 3,00 . 108m/s. De acordo com a teoria ondulatória da luz, qual o módulo da velocidade de propagação da luz no vidro?
3. Um raio luminoso monocromático, que se propaga no ar, atinge a
superfície livre de um líquido em repouso segundo um ângulo de
incidência de 60°. Sabendo-se que o ângulo de refração correspondente
vale 30°, determine o índice de refração absoluto deste líquido. O índice
de refração absoluto do ar vale 1.
4. Um feixe de luz monocromática, que se propaga no ar (nar = 1),
penetra numa barra de vidro de índice de refração absoluto igual a 2.
Determine o ângulo de refração, quando o feixe incidente forma um
ângulo de 45° com a normal.
5. (FUND. CARLOS CHAGAS) – Na figura a seguir, está representado o trajeto de um raio de luz monocromática, que passa de
um meio (1) para um meio (2). Qual é o índice de refração do meio (2)
em relação ao meio (1)?
(S é a superfície de separação dos dois meios e as distâncias AO e OB
são iguais.)
5. (FEI) – Deseja-se formar uma imagem real de um objeto sobre uma
tela que dele dista 5,0m, por meio um espelho esférico. A distância do
objeto ao espelho deve ser igual a 15cm, e a altura do objeto é de
2,0cm. Determine
a) o tipo de espelho;
b) o tamanho da imagem e se é direita ou invertida.
6. (FUND. CARLOS CHAGAS) – O objeto BB' dista igualmente
(2x) de um espelho plano (P) e de um espelho côncavo (C) de raio igual
a 4x. O sistema é centrado e está esquematizado na figura a seguir:
6. (CESGRANRIO) – Entre as direções indicadas pelas letras A, B,
C, D e E de um raio luminoso monocromático que passa do vidro para
o ar, qual a única que pode representar a situação real, sabendo-se que
o raio emergente tem a direção xy, indicada na figura?
a) A
b) B
c) C
d) D
e) E
A que distância de C se formará a primeira imagem resultante de duas
reflexões sucessivas, a primeira em P e a segunda em E?
112 –
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 113
7. A figura mostra um raio de luz monocromática passando do meio
A ao meio B. Conforme a figura, podemos afirmar que
a) em A o módulo da velocidade da luz é maior.
b) o módulo da velocidade de propagação da luz é o mesmo nos dois
meios.
c) B é o meio mais refringente.
d) A é o meio de maior índice de refração absoluto.
e) o ângulo de incidência é maior do que o de refração.
FRENTE 3
MÓDULOS 11 e 12
ENERGIA ELÉTRICA, POTÊNCIA ELÉTRICA
E POTÊNCIA DISSIPADA PELO RESISTOR
1. (VUNESP-SP) – Nas residências, nos escritórios e nas fábricas, a
eletricidade é disponibilizada em corrente alternada (CA). Ela é gerada
em 25 000 V, transmitida em 750 000 V e chega a nossas residências
em 110 V ou 220 V. Na transmissão de eletricidade em CA, deve-se
considerar: a tensão elétrica V e a corrente I. A transmissão à alta tensão
elétrica implica que a corrente associada é baixa, e quando a
transmissão é realizada à baixa tensão elétrica, a corrente associada é
alta. Corrente alta implica geração de muito calor e, por isso, a
transmissão de potência elétrica à longa distância é feita em alta tensão.
O dispositivo usado para aumentar ou diminuir a tensão alternada na
rede elétrica é denominado
a) transformador.
b) capacitor.
c) multímetro.
d) resistor.
e) potenciômetro.
Que outros aparelhos podem estar ligados ao mesmo tempo que o chuveiro
elétrico sem “queimar” o fusível?
a) geladeira, lâmpada e TV.
b) geladeira e TV.
c) geladeira e lâmpada.
d) geladeira.
e) lâmpada e TV.
4. (FUVEST-SP)
a) Qual a resistência de uma lâmpada de 220V e 60W?
b) Supondo que a resistência varia pouco com a temperatura, qual a
potência dissipada quando a lâmpada é ligada a uma tomada de
110V?
5. (FATEC) – Um resistor ôhmico, de resistência R = 20Ω, submetido
a uma ddp de 200 V, é percorrido por uma corrente elétrica de
intensidade 10 A e dissipa uma potência de 2000 W.
Se o mesmo resistor for submetido à ddp de 100 V, a intensidade da
corrente que o percorrerá, em ampéres, e a potência que dissipará, em
watts, serão, respectivamente,
a) 10 e 1000.
b) 10 e 500.
c) 5 e 4000.
d) 5 e 2000.
e) 5 e 500.
6. (FATEC-SP) – Um fio de extensão está ligado numa tomada de
110V. Esse fio de extensão tem três saídas, nas quais estão ligados um
aquecedor de 500W, uma lâmpada de 100W e um secador de cabelos
de 200W. Esses aparelhos estão ligados em paralelo e permanecem
funcionando por 5,0 minutos.
O valor aproximado da corrente elétrica que passa pelo fio e o gasto de
energia com esses três aparelhos, quando funcionando simultaneamente, após 5,0 minutos, são, respectivamente:
a) 1A e 8,3.105J
b) 2A e 7,2.105J
c) 4A e 5,4.105J
d) 7A e 2,4.105J
e) 10A e 1,2.105J
2. (MACKENZIE) – Um chuveiro elétrico apre sen ta a inscrição
2200W / 4400W – 220V
verão inverno
e, ligado corretamente, está prote-
gido, na rede que o alimenta, por um fusível com tolerância de até 30A.
Se ligarmos, em paralelo ao chuveiro, sob a mesma d. d. p. de 220V,
uma torneira elétrica com a inscrição 2000W – 220V , poderemos
afirmar que
a) o fusível queimará somente se o chuveiro estiver ligado no “verão”.
b) o fusível queimará somente se o chuveiro estiver ligado no
“inverno”.
c) o fusível queimará de qualquer forma, ou seja, tanto se o chuveiro
estiver ligado no “verão” como no “inverno”.
d) o fusível não queimará de maneira alguma.
e) o fusível queimará mesmo sem ser ligada a torneira.
3. (FUVEST-SP) – No circuito elétrico residencial esquematizado a
seguir, estão indicadas, em watts, as potências dissipadas pelos seus
diversos equipamentos. O circuito está protegido por um fusível, F, que se
funde quando a corrente ultrapassa 30A, interrompendo o circuito.
MÓDULO 13
PONTE DE WHEATSTONE
1. (UNICAMP) – No circuito abaixo, a corrente na resistência 5,0
é nula.
Determine o valor da resistência X que faz parte da Ponte de Wheatstone.
– 113
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 114
2. A Ponte de Wheatstone da figura está em equilíbrio.
Entre B e C, temos uma lâmpada (L).
2. (VUNESP) – Um corpo de peso P está pendurado em duas cordas
inextensíveis e de pesos desprezíveis, amarradas nos pontos A e B do
teto e em C, como mostra a figura a seguir:
Quais as intensidades das forças que os fios aplicam nos pontos A e B
do teto?
Assinale certo (C) ou errado (E).
I. A lâmpada está apagada.
II. A bateria de 6,0V não é percorrida por corrente elétrica.
III. O valor da resistência R é 3,0.
a) CCC
b) CEC
c) ECE
d) EEE
e) EEC
3. Na figura a seguir, as trações nos fios ideais AB e BC valem, respectivamente: (dados cos 60° = 0,50 e sen 60° = 0,86)
a) 50N e 60N;
b) 172N e 200N;
c) 86N e 100N;
d) zero e 100N;
e) 200N e 100N.
3. Considere o circuito esquematizado abaixo.
Determine
a) a resistência do resistor equivalente.
b) a intensidade da corrente que percorre o gerador.
4. O sistema da figura seguinte, para chegar à posição de equilíbrio,
fez com que a mola M fosse alongada de 0,50cm. Sabendo-se que as
massas dos fios e da mola são desprezíveis e que o peso P vale
1,4 . 102N, determine
MÓDULO 14
ESTÁTICA DO PONTO MATERIAL
1. (UFSE) – Um objeto de peso 50N é equilibrado por duas cordas,
que formam 30° com a horizontal.
A tração em cada corda tem módulo, em newtons,
a) 25
b) 50
c) 70
d) 100
114 –
e) 200
a) a tração no fio AB.
b) a constante elástica da mola.
Considere cos 45° = 0,70.
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 115
5. (PUC-PR) – Conforme os dados da figura, a compressão na barra
AB (peso desprezível) e a tração no fio ideal BC têm, respectivamente,
valores iguais a:
a) 400 3 N e 800N
3N
b) 200N
e 800 3N
c) 400N
e 400 d) 400N
e 200N
e) 200 3 N e 400N
3. (UFPR) – A figura abaixo representa um poste homogêneo de
massa total 50kg apoiado sobre o suporte A.
a) Determine a massa do bloco B, de dimensões desprezíveis, que
deve ser colocado na extremidade direita para que o sistema fique
em equilíbrio, permanecendo o poste na posição horizontal.
b) Calcule a força que o suporte exerce sobre o poste nas condições do
item anterior.
(Considere g = 10m/s2)
4. A barra AB, representada na figura, é homogênea, tem massa de
100kg e está apoiada em suas extremidades A e B.
Nas posições indicadas, estão pendurados dois blocos com as massas
indicadas.
MÓDULO 15
ESTÁTICA DO CORPO EXTENSO
1. (UFPR) – Cinco homens sustentam um corpo de peso P numa
prancha horizontal de comprimento 4,0m e peso desprezível comparado com P. Estando dois homens na extremidade A da prancha e
três na extremidade B, a que distância de A deve estar o corpo para
que todos os homens façam a mesma força?
Calcule as intensidades das forças de reação nos apoios A e B. Adote
g = 10 m.s–2.
5. (MACKENZIE) – A barra AB, articulada em A, é homogênea,
pesa 30N e se mantém em equilíbrio horizontal, como mostra a figura.
Despreze os atritos. O fio BC e a polia são ideais.
Adote g = 10m/s2. Qual a massa m do corpo suspenso?
2. (FUVEST) – Dois homens estão carregando uma viga de madeira
nas posições A e B indicadas na figura. Se a viga é homogênea e pesa
40kgf, qual a carga suportada por cada um?
– 115
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 116
6. (VEST-RIO) – Um menino, de massa 40kg, está sobre uma tábua
de 2,0m de comprimento a 0,5m do apoio A, conforme a figura a
seguir:
Assinale certo (C) ou errado (E), para as figuras II e III.
I) Na fig. II, temos, finalmente, o polo N separado do polo S.
II) Na fig. II, os pedaços atraem-se, pois B é N e C é S.
III) Na fig. III, os pedaços atraem-se, pois B é N e C é S;
IV) Na fig. III, os pedaços repelem-se, pois B e C são S, enquanto A e
D são N.
Desprezando-se os pesos da tábua e da vara de pescar e considerandose g = 10m/s2, as reações nos apoios A e B valem, em newtons, respectivamente:
a) 350 e 400
b) 300 e 100
c) 200 e 200
d) 250 e 150
e) 500 e 350
3. Represente a força magnética sobre a carga q, lançada perpendi→
cularmente ao campo magnético ( B), com velocidade (→
v ).
MÓDULO 16
ÍMÃS, CAMPO MAGNÉTICO E
FORÇA MAGNÉTICA DE LORENTZ
1. Dispomos de um ímã em forma de barra no qual N e S indicam os
seus dois polos: norte e sul. Vamos dividir a barra em três pedaços,
como na fig. II.
Podemos ter certeza de que
a) temos, finalmente, o polo norte separado do sul.
––––
b) em A temos o N; em D temos o S; em B’C’ não temos polaridade
magnética.
c) temos três ímãs na fig. II, sendo que o ímã do meio terá em B’ um
S e em C’ um N.
d) temos, na fig II, três ímãs, sendo que A é N, B é S, C é N, D é S, B’
é S e C’ é N.
––– –––– –––
e) temos três ímãs: AB, B’C’ e CD; os polos N são A, B’ e C.
2. Quebre um ímã em dois pedaços idênticos. Coloque-os invertidos
(fig. II) e em paralelo (fig. III).
116 –
Obs.: a carga q+ é positiva.
4. Nas três figuras, a carga q– é negativa (um elétron). Represente a
força magnética.
5. (MACKENZIE-SP-MODIFICADA) – Entre os ímãs A e B, existe um campo de indução magnética uniforme, paralelo ao eixo y, e os
efeitos de borda são desprezados. Uma carga elétrica puntiforme + q
chega ao ponto O do sistema de eixos cartesianos, adotado como re→
ferencial, com velocidade v de mesma direção e sentido orientado pelo
eixo x.
A força magnética que age na partícula tem
a) a direção e o sentido do eixo z.
b) a direção do eixo z, mas sentido oposto ao deste.
c) a direção do eixo y e sentido oposto ao deste.
d) a direção e o sentido do eixo y.
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 117
MÓDULO 17
MOVIMENTO DE UMA
PARTÍCULA ELETRIZADA EM UM
CAMPO MAGNÉTICO UNIFORME
1. (CEFET-PI) – Três espécies de partículas que se propagam em
linha reta têm a mesma velocidade e a mesma carga elétrica, porém as
massas são diferentes. Quando essas partículas penetram num campo
magnético uniforme, saindo do plano da página, com velocidade
perpendicular ao campo, observa-se a formação de três trajetórias
circulares de raios diferentes, como mostra a figura.
Marque a alternativa correta.
a) As partículas têm cargas negativas.
b) A partícula de maior massa descreve a trajetória de menor raio,
trajetória 3.
c) A partícula de maior massa descreve a trajetória de raio
intermediário, trajetória 2.
d) A partícula de menor massa descreve a trajetória de maior raio,
trajetória 3.
e) As partículas têm cargas positivas.
2. (FUND. CARLOS CHAGAS) – Uma partícula eletricamente
carregada, que tem velocidade inicial →
v 0 no ponto R, descreve a
trajetória semicircular no plano da página, de R para S, conforme
mostra a figura abaixo.
A partícula percorre esta trajetória porque um campo uniforme está
atuando nesta região.
Este é um campo
a) elétrico na direção y.
b) elétrico na direção x.
c) elétrico perpendicular à página.
d) magnético perpendicular à página.
e) magnético na direção x.
3. (UFMG) – Quanto à trajetória de uma carga elétrica pontual, que
→
→
se move com velocidade v em um campo magnético uniforme B, é
correto afirmar que
a) será sempre retilínea.
→
b) será sempre circular em torno de B.
c) será sempre parabólica.
→ →
d) dependerá das direções de B e v .
e) dependerá da intensidade do campo magnético.
4. Uma partícula de massa m, carregada com uma carga q positiva,
→
penetra num campo magnético B , com uma energia cinética:
→
→
E = 1/2mv2, tal que v é perpendicular a B . Marque a afirmativa correta.
a) Estando a partícula carregada, movendo-se em um campo
magnético, ela sofre a ação de uma força; então há trabalho
realizado sobre ela.
b) Sua energia cinética é constante, porque o trabalho realizado pela
força magnética é nulo.
c) A trajetória descrita pela partícula dentro do campo magnético será
retilínea.
d) De acordo com a Lei de Faraday, a energia da partícula será
constante.
5. (UNESP) – Um próton, de carga 1,6 x 10–19 C e massa
1,6 x 10–27kg, move-se com velocidade de 8 x 106 m/s numa dada
direção, até o momento em que entra numa região onde existe um
campo magnético. Esse campo tem intensidade de 2,5 T e direção
formando um ângulo de 30° com a direção na qual se movia o próton.
A aceleração inicial do próton, ao entrar na região desse campo
magnético, é
a) 1,8 x 1015 m/s2
b) 1,6 x 1015 m/s2
c) 1,4 x 1015 m/s2
d) 1,2 x 1015 m/s2
e) 1,0 x 1015 m/s2
6. (FUVEST-SP) – Um próton (carga q e massa m) penetra em uma
→
região do espaço tomada por um campo magnético uniforme B
perpendicular à página.
C
q
Sendo dados v = 107m/s, R = 2m e ––– = 108 –––– , determine B.
kg
m
7. (MACKENZIE-SP) – Dois corpúsculos, A e B, de massas mA e
mB, carregados eletricamente com cargas respectivamente iguais a + q
e + 4q, penetram com mesma velocidade v em um campo magnético
– 117
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 118
uniforme. A direção da velocidade das cargas é perpendicular às linhas
mA
de indução desse campo. A relação –––––
, entre as massas dos cormB
2. Entre os polos de dois ímãs, colocamos um condutor retilíneo percorrido por uma corrente elétrica de intensidade i.
púsculos, para que eles descrevam trajetórias de mesmo raio, é:
1
a) –––
4
1
b) –––
2
c) 2
d) 3
e) 4
MÓDULO 18
CAMPO MAGNÉTICO
GERADO POR CONDUTOR RETILÍNEO
1. Usando a regra da mão esquerda, determine o sentido da força
magnética sobre o fio retilíneo percorrido por uma corrente contínua de
intensidade i, das figuras de 1 até 6.
a) Determine o sentido da força magnética que atua no condutor.
b) Se invertermos o sentido da corrente elétrica, como fica o novo
sentido da força magnética?
c) Se trocarmos de posição o polo N com o polo S, o que ocorre com
o sentido da força magnética?
3. (FAAP) – Um condutor retilíneo de comprimento ᐉ = 0,20m,
percorrido por uma corrente i = 2,0A, é imerso em um campo
magnético uniforme de indução B = 2,0 . 104T. Determinar o
intensidade da força magnética que atua sobre o condutor nos casos:
a) o condutor é disposto paralelamente às linhas de indução do campo.
b) o condutor é disposto perpendicularmente às linhas de indução do
campo.
4. (MACKENZIE-SP) – Um condutor retilíneo de comprimento
0,5m é percorrido por uma corrente de intensidade 4,0A. O condutor
está totalmente imerso num campo magnético de intensidade 10–3T,
formando com a direção do campo um ângulo de 30°. A intensidade da
força magnética que atua sobre o condutor é:
a) 103N
b) 2 . 10–2N
c) 10–4N
d) 10–3N
e) Nula
FRENTE 1
MÓDULO 12
MÓDULO 11
1) a)
b)
1ª categoria: grandezas escalares
2ª categoria: grandezas vetoriais
Área
1ª categoria
Mecânica
energia
Eletricidade
2) E
118 –
3) A
potencial elétrico
4) a) 2,0N F 14,0 N
b) 10,0 N
2) a) 4,0 . 1016 rad/s
b) 1,5 . 10–16s
c) 8,0 . 1022m/s2
4) a) 3,0 . 102 rpm
b) 3,0 m/s
1)
2ª categoria
quantidade de
movimento
campo elétrico
5) B
25,0m
5) a) 30cm/s
b) anti-horário e 15rpm
c) horário e 3,0s
6) 12,2 N
6) A
3) a) 3 . 10–10m/s2
b) 2 . 108 anos
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 119
c)
MÓDULO 13
1) a) 5,0m/s
2) E
b) 1,5m/s
c) 10m/s2
4) C
5) C
6) a) 0,8s
7) A
b) 11m/s
2) A
3) E
5) B
6) a) 6,0m/s2
b) 3,0kN
d)
2) C
Mmg
T = –––––––
M+m
4) E
→
5) Na figura 1, a força P deve acelerar o carrinho e o bloco.
→
Na figura 2, a mesma força P deve acelerar apenas o carrinho
e por isso a aceleração será maior.
6) a = 5,0m/s2; FBA = 25,0N; T = 100N
4) a) 5,0kg
b) 2,4m/s2
MÓDULO 18
4) A
5) C
MÓDULO 16
1) a) 2,0m/s2
b) 4,0N
5) a) 66N
b) 60N
Substituindo-se o valor do módulo da aceleração na
equação (1), vem:
T = Ma ⇒
MÓDULO 15
1) E
2) D
3) A
6) a) 12N, vertical, para baixo
b) 10N, vertical, para cima
mg
a = –––––––
m+M
3) a) 20m/s e 10m/s2
b) 0,8s
MÓDULO 14
1) A
A partir da equação (3):
mg = (M + m)a, vem:
3) E
1) E
2) a) 2,0m/s2; para baixo
b) Descendo com movimento acelerado ou subindo com movimento retardado.
3) A 4) a) 4,0N
5) a) 2,0m/s2
6) A
b) 1,0s
b) 24N
c) 48N
FRENTE 2
4) a) 4,0m/s2
b) 44,0N
6) 1,0N
MÓDULO 11
1) A
2) A
3) A
4) B
5) D
6) A
MÓDULO 17
1) a) 36N
b) 24N
3) a)
2) a) 4,0m/s2
b) 1,2N
MÓDULO 12
1)
C
2) B
3) 40cm
4) C
3) D
4) D
MÓDULO 13
1)
b)
(2).
NA é a intensidade da reação normal de apoio sobre o bloco A; PA e PB são os pesos de A e B;
T representa a intensidade da força que o fio aplica em
cada um dos blocos.
(1) PFD(A): T = Ma
(2) PFD(B): mg – T = ma
(3) PFD(A + B): mg = (M + m)a
Nota: A equação (3) é obtida da soma das equações (1) e
C
2) 90m
5) D
MÓDULO 14
1) C
5) A
2) B
6) 2d
3) E
7) C
4) D
8) D
MÓDULO 15
1) 60cm
2) a) 5,0m/s
b) 10m/s
3) C
4) C
5) C
– 119
C2_3a_Soroc_Fis_Exerc_alelex_2014 03/01/14 13:26 Página 120
MÓDULO 16
1)
2)
3)
4)
MÓDULO 13
1) 6,0
real; invertida; maior
virtual; direita; menor
D
a)
2) B
3) a) 10
b) 6,0A
MÓDULO 14
3
P
P 2) ––––––– e ––––
2
2
1) B
4) a) 2,0.102N
b) 2,8.104N/m
3) B
5) A
MÓDULO 15
1) 2,4m
3) a) 12,5kg
b) 625N
5) 1,5kg
b)
2) A = 15kgf
e B = 25kgf
4) NA = 1,25kN e NB=1,75kN
6) B
MÓDULO 16
1) E
5) E
6) real; invertida; menor
2) I-E II-C III-C IV-E
→
F
b)
F
b)
c)
→
F
c)
2) 2,0m
3) 4f
5) a) côncavo
b) 68,7cm e invertida
6) 3x
4) a) F
→
MÓDULO 17
1) A
4) convexo; |f| = 3,6m
→
3) a)
5) A
→
F
→
F
MÓDULO 17
1) E
5) E
2) D
6) 5,0 . 10– 2 T
3) D
7) A
MÓDULO 18
1) 4/3
5) 0,60
3) 3
7) D
2) 2,00 . 108m/s
6) C
4) 30°
120 –
3) E
4) a) 807Ω
b) 15W
→
Fm = 0
→
Fm = →
Fm ↓
Fig. 2
Fig. 4
Fig. 6
→
Fm = →
Fm ↓
→
Fm ←
2) a) Vertical, para baixo.
b) Inverterá: vertical, para cima.
c) Inverterá em relação ao modo inicial.
MÓDULOS 11 e 12
2) D
→
1) Fig. 1
Fig. 3
Fig. 5
FRENTE 3
1) A
MÓDULO 18
5) E
6) D
→
→
3) a) Fm = 0
4) D
b) Fm = 8,0 x 103N
4) B