Circunferências

Circunferências
1 - Os seus elementos
A
Raio
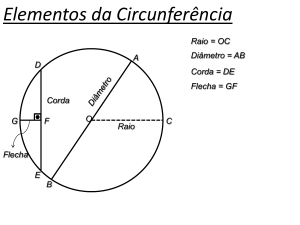
O – Centro da circunferência
[OA] – Raio da circunferência
[BC] – Diâmetro da circunferência
[DE] – Corda da circunferência
O .
B
C
Diâmetro
D
Corda
Corda – segmento de recta que une dois pontos da
circunferência;
E
Diâmetro da circunferência – é a maior das cordas
O diâmetro divide a circunferência em duas semi-circunferências
2 - Posição relativa de uma recta e uma circunferência
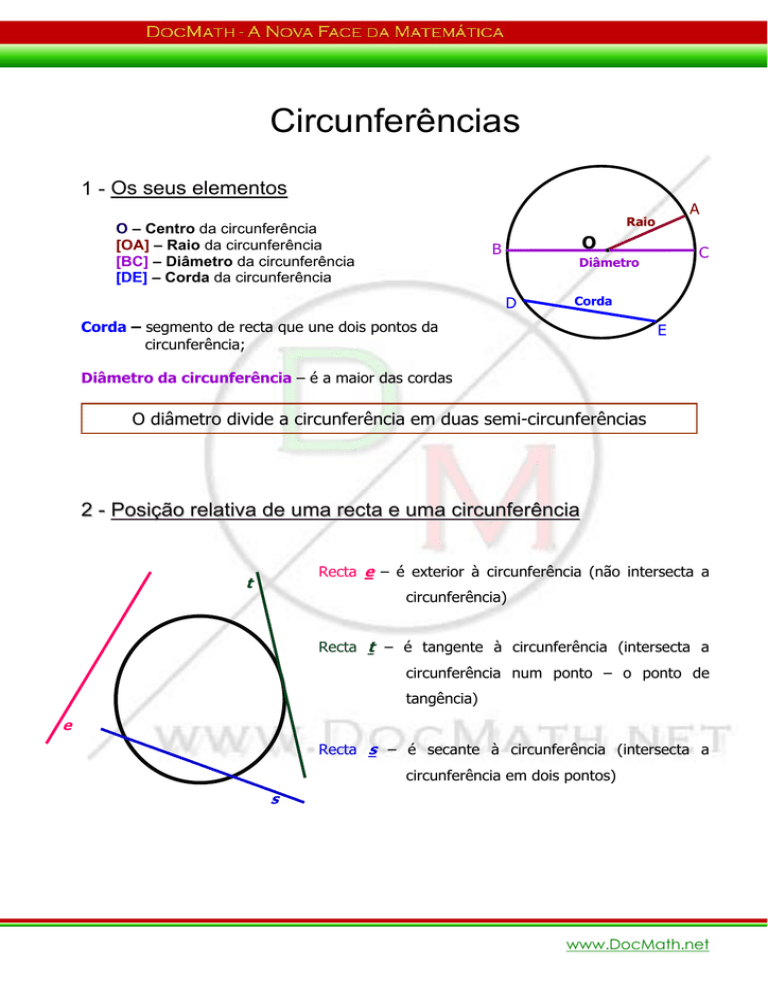
Recta e – é exterior à circunferência (não intersecta a
t
circunferência)
Recta t – é tangente à circunferência (intersecta a
circunferência num ponto – o ponto de
tangência)
e
Recta s – é secante à circunferência (intersecta a
circunferência em dois pontos)
s
www.DocMath.net
3 – Propriedades de cordas paralelas
Sabe-se que [AB] // [CD].
A
B
Então:
- os arcos AC e BD são geometricamente iguais;
- as cordas [AC] e [BD] são geometricamente iguais.
O.
D
C
Propriedade 1:
Arcos compreendidos entre cordas paralelas são
geometricamente iguais.
Propriedade 2:
Cordas compreendidas entre cordas paralelas são
geometricamente iguais.
4 - Recta Tangente à Circunferência
90º
Raio
T
t - Recta tangente à circunferência em T
O.
t
Propriedade 3:
Qualquer tangente a uma circunferência é perpendicular ao raio
no ponto de tangência.
www.DocMath.net
5 - Ângulos ao Centro
A
.
O
B
Ângulo ao centro – tem o vértice
no centro da circunferência
’ ângulo AOB ⇨ arco AB
e
arco AB ⇨ ângulo AOB
’ ângulo AOB ⇨ corda [AB] e
corda [AB] ⇨ ângulo AOB
’ corda [AB] ⇨ arco AB
arco AB ⇨ corda [AB]
e
5.1 - Propriedades de Ângulos ao Centro
O
A
.
B
C
-
O arco AB é geometricamente igual ao
arco CD;
-
As
cordas
[AB]
e
geometricamente iguais.
[CD]
são
D
Propriedade 4:
A ângulos ao centro iguais correspondem arcos iguais e cordas iguais.
www.DocMath.net
5.2 – Circunferências Concêntricas
Observa as seguintes circunferências concêntricas (têm o mesmo centro):
O
A
.
A’
Temos que:
A’’
AÔB = AB =A’B’ = A’’B’’
B B’
B’’
6 - Ângulos Inscritos num arco de Circunferência
Exemplos:
.
.
O
O
.
O
Ângulo Inscrito num arco de Circunferência - é todo o ângulo com vértice sobre a
circunferência e cujos lados contêm
cordas.
6.1 - Arco Capaz e Arco Compreendido
A
V
- O arco AVB é o arco capaz do ângulo inscrito
.
AVB;
O
- O arco AB é o arco compreendido entre os lados
B
do ângulo AVB.
www.DocMath.net
6.2 - Ângulos Inscritos num mesmo arco de Circunferência
A
V
β
β
V’
β
V’’
B
Propriedade 5:
Ângulos inscritos num mesmo arco de circunferência são
geometricamente iguais, isto é, têm a mesma amplitude.
6.3 - Ângulos Inscritos numa Semi-circunferência
V
A
V’
O
V’’
.
[AB] é o diâmetro da circunferência
B
Propriedade 6:
Qualquer ângulo inscrito numa semi-circunferência é recto, isto é,
tem amplitude igual a 90º.
www.DocMath.net
7 - Ângulos ao Centro e Ângulos Inscritos
A
V
β/2
O
.
β
β
B
Propriedade 7:
A amplitude de um ângulo inscrito é igual a metade da amplitude do
arco compreendido entre os seus lados
Propriedade 8:
A amplitude de um ângulo inscrito é igual a metade da amplitude do
ângulo ao centro correspondente.
www.DocMath.net