Apostila_Corrente_Alternada[1] - AC current

Visualização do documento
Apostila_Corrente_Alternada[1].doc
(840 KB) Baixar
Corrente Alternada
1. Geração
Denominamos alternador ao gerador de corrente alternada, assim como denominamos dínamo ao
gerador de corrente contínua. Os geradores são máquinas destinadas a converter energia mecânica
em energia elétrica. A transformação de energia nos geradores fundamenta-se nas Leis de Faraday
e Lenz. A Lei de Faraday afirma que todo condutor imerso em um campo magnético variável
produz uma força eletromotriz induzida (femi). A Lei de Lenz complementa a Lei de Faraday
informando que a polaridade da femi produz uma corrente induzida que tende a se opor à causa
que lhe originou.
Os alternadores pertencem à categoria das máquinas síncronas, isto é, máquinas cuja rotação é
diretamente relacionada ao número de pólos magnéticos e a freqüência da força eletromotriz. Não
há, basicamente, diferenças construtivas entre um alternador e um motor síncrono, podendo um
substituir o outro sem prejuízo de desempenho.
Assim, um alternador quando tem seu eixo acionado por um motor, produz energia elétrica nos
terminais e, ao contrário, recebendo energia elétrica nos seus terminais, produz energia mecânica
na ponta do eixo, com o mesmo rendimento.
A indução magnética ocorre sempre que há movimento relativo entre um condutor e um campo
magnético. O gerador elementar, concebido por Michael Faraday em 1831, na Inglaterra e mais
ou
menos na mesma época por Joseph Henry, nos Estados Unidos, era constituído por uma espira que
girava entre os pólos de um ímã, semelhante à figura:
No gerador elementar acima, uma espira de fio girando em um campo magnético produz uma fem.
Os terminais da bobina são ligados ao circuito externo por meio dos anéis coletores e escovas.
A força eletromotriz e a corrente de um gerador elementar mudam de direção cada vez que a espira
gira 180°. A tensão de saída deste gerador é alternada, conforme a figura abaixo.
Faraday estabeleceu, ainda, que os valores instantâneos da força eletromotriz (ou tensão) podiam
ser calculados pela relação:
Faraday estabeleceu, ainda, que os valores instantâneos da força eletromotriz (ou tensão) podiam
ser calculados pela relação:
Onde:
e = força eletromotriz;
B = indução do Campo Magnético;
l = comprimento do condutor;
v = velocidade linear de deslocamento do
condutor e,
θ = ângulo formado entre B e v;
O campo magnético da figura acima é constituído por ímãs naturais. Para que seja possível
controlar tensão e corrente em um alternador, o campo magnético é produzido por ímãs artificiais,
formados por bobinas alimentadas com corrente contínua suprida por uma fonte externa e
controlada por um regulador de tensão.
2. Definições em CA
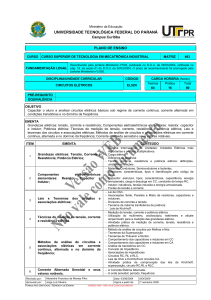
CICLO: É um conjunto de valores que se repetem periodicamente. O tempo necessário para que
a onda senoidal complete um ciclo é chamado de PERÍODO (T), e é dado em segundos (s).
FREQUÊNCIA: Exprime a quantidade de períodos de uma onda no tempo de um segundo.
A unidade de freqüência é Hertz (Hz) que é igual a ciclos/segundo.
VELOCIDADE ANGULAR (ω): É o ângulo descrito na unidade de tempo.
3. CURVA DE VARIAÇÃO DE UMA GRANDEZA ALTERNADA
Uma corrente senoidal pode ser representada pela componente vertical de um vetor de módulo Ip
(corrente de pico) que gira no sentido anti-horário com velocidade angular constante w = 2πf.
Nota-se a semelhança com um número complexo. Assim podemos escrever:
i = Ip(cos wt + j sen wt) = Ip ejwt
e para a tensão:
v = Vp(cos wt + j sen wt) = Vp ejwt
E, para indicar a representação complexa, usamos I em vez de i e V em vez de v.
Numa grandeza senoidal temos os seguintes tipos de valor:
VALOR MÁXIMO: É o máximo valor que uma grandeza pode assumir. Também é conhecido
como Valor de Pico (VP) ou de Crista. Os valores compreendidos entre o pico de máximo positivo
e o de máximo negativo são chamados de Valor Pico-a-Pico(VPP = 2.VP).
VALOR MÉDIO: O valor médio de uma grandeza senoidal, quando considerado de um período
inteiro, é nulo, pois a soma dos valores instantâneos relativa à semi-onda positiva é
igual à negativa, sendo sua resultante constantemente nula.
Pela razão exposta, o valor médio de uma grandeza alternada senoidal deve ser considerado como
sendo a média aritmética dos valores instantâneos no intervalo de meio período. Este valor médio
é representado pela ordenada média da semi-onda que indica os valores instantâneos.
VALOR EFICAZ: Suponha-se que dois circuitos elétricos iguais de resistência R são atravessados
um por corrente contínua e outro por corrente alternada. Se os dois circuitos considerados
produzirem a mesma quantidade de calor, se dirá que há equivalência entre as duas correntes. Não
se pode, porém dizer que o valor médio da corrente alternada corresponde ao da corrente contínua,
pois o valor médio de uma grandeza alternada é zero.
Para expressar a equivalência entre as duas correntes se dirá que a intensidade da corrente contínua
é igual ao valor eficaz da corrente alternada. Isto é, uma corrente alternada que possui o valor
eficaz de 10 A, quando atravessar um circuito elétrico produzirá a mesma quantidade de calor que
uma corrente contínua, cuja intensidade é 10 A.
O valor eficaz é o valor de uma corrente contínua que produz a mesma dissipação de calor em um
resistor. É também é chamado de rms (root mean square). A maioria dos voltímetros e
amperímetros para corrente alternada indicam valores em rms. Entretanto, é importante lembrar
que instrumentos comuns só indicam o valor rms correto para tensões ou correntes senoidais. Para
outras formas devem ser usados tipos mais sofisticados, chamados de true-rms.
Assim, por exemplo, 110 Volts eficazes correspondem a uma amplitude de 155.6 V e uma
amplitude pico-a-pico de 311 V.
Resumindo:
FATOR DE FORMA: É a relação entre o valor eficaz e o valor médio de uma onda. No caso de
uma onda senoidal temos:
ÂNGULO DE FASE: O ângulo de fase entre duas formas de onda de mesma freqüência é a
diferença angular num dado instante. Por exemplo, o ângulo de fase entre as ondas A e B da figura
abaixo é de 90°. Considere o instante para 90°. O eixo horizontal representa as unidades de tempo
em ângulos. A onda B começa com seu valor máximo e cai para zero em 90°, enquanto a onda A
começa em zero e cresce até seu valor máximo em 90°. A onda B atinge seu valor máximo 90° na
frente da onda A; logo, a onda B está adiantada relativamente onda A de 90°. Este ângulo de fase
de 90° entre as ondas A e B é mantido durante o ciclo completo e todos os ciclos sucessivos. Em
qualquer instante, a onda B passa pelo valor que a onda A terá 90° mais tarde.
FASORES: Na comparação de ângulos de fase ou simplesmente fases de correntes e tensões
alternadas, é mais conveniente a utilização de diagrama de fasores correspondentes às formas de
onda da tensão e da corrente. Um fasor é uma entidade com módulo e sentido. Os termos fasor e
vetor são usados para representar quantidades que possuem um sentido. Entretanto, o fasor varia
com o tempo, enquanto o vetor tem sentido fixo no espaço.
4. Formas de Representação de um Sinal Senoidal
4.1. Forma de Onda
Representa graficamente a variação do sinal senoidal em função do tempo. O exemplo abaixo
mostra a representação por forma de onda de duas tensões senoidais, A e B.
4.2. Diagrama Fasorial
Representa fasorialmente os sinais senoidais. Para os sinais senoidais A e B, do exemplo acima,
teremos o diagrama fasorial, com valores de pico:
4.3. Expressão trigonométrica
Representa sob forma de função trigonométrica os sinais senoidais. Para o exemplo acima teremos:
vA = 220.sen (120.π.t + 30°) [V]
vB = 400.sen (120.π.t) [V]
4.4. Números Complexos
Representa sob forma de números complexos os sinais senoidais. Para o exemplo acima teremos:
VA = 220 |30° [V]
60 Hz
VB = 400 |0° [V]
Nota-se que na representação por números complexos não é possível identificar a freqüência,
devendo esta ser informa separadamente.
4.5. Tipos de Cargas em Circuitos CA
4.5.1. Cargas Resistivas Puras
Em um circuito resistivo puro em CA, as variações na corrente ocorrem em fase com a tensão
aplicada.
Expressões trigonométricas:
Forma de onda:
Diagrama fasorial:
Números complexos:
4.5.1.1. Potência em Cargas Resistivas Puras
A figura abaixo apresenta a variação da potência em função do tempo para um circuito resistivo
puro. Nota-se que a potência apenas assume valores positivos, sendo denominada
de potência ativa, uma vez que representa a potência fornecida à carga, produzindo trabalho útil.
A potência média de um circuito resistivo puro pode ser determinada multiplicando-se a tensão
rms pela corrente rms:
4.5.2. Cargas Capacitivas Puras
Em um circuito capacitivo puro em CA, a corrente está adiantada 90° em relação à tensão aplicada.
Derivando a equação acima, temos:
Portanto, para um circuito capacitivo puro teremos as seguintes expressões trigonométricas:
Formas de onda:
Diagrama fasorial:
Números complexos:
4.5.2.1. Reatância Capacitiva
A reatância capacitiva XC é a dificuldade imposta pelo campo elétrico do capacitor à passagem da
corrente elétrica. Sua unidade é o ohm.
4.5.2.2. Potência em Cargas Capacitivas Puras
A figura abaixo apresenta a variação da potência em função do tempo para um circuito capacitivo
puro. Nota-se que a potência assume valores positivos e negativos, sendo seu valor médio igual a
zero. Esta potência é denominada potência reativa capacitiv...
Arquivo da conta:
engenhariaeletricasantos
Outros arquivos desta pasta:


analise_circuito_ca.rar (17135 KB)
Circuitos Elétricos Corrente Contínua E Corrente Alternada - Otávio Markus - Editora
Érica.pdf (14497 KB)
 Apostila Padrão para Corrente.pdf (2700 KB)
 Apostila_Corrente_Alternada[1].doc (840 KB)
 circuito polifásico 2.pdf (80 KB)
Outros arquivos desta conta:

Direct Current
Relatar se os regulamentos foram violados








Página inicial
Contacta-nos
Ajuda
Opções
Termos e condições
Política de privacidade
Reportar abuso
Copyright © 2012 Minhateca.com.br