projeto específicas - uerj

PROJETO ESPECÍFICAS - UERJ
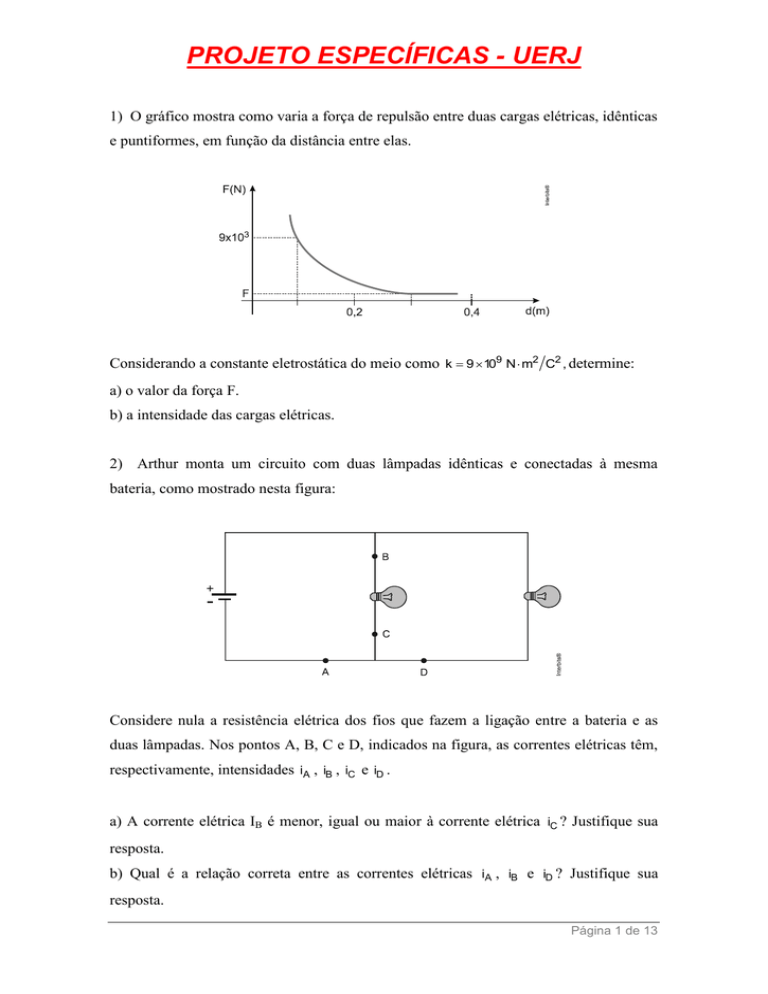
1) O gráfico mostra como varia a força de repulsão entre duas cargas elétricas, idênticas
e puntiformes, em função da distância entre elas.
Considerando a constante eletrostática do meio como k  9  109 N  m2 C2 , determine:
a) o valor da força F.
b) a intensidade das cargas elétricas.
2) Arthur monta um circuito com duas lâmpadas idênticas e conectadas à mesma
bateria, como mostrado nesta figura:
Considere nula a resistência elétrica dos fios que fazem a ligação entre a bateria e as
duas lâmpadas. Nos pontos A, B, C e D, indicados na figura, as correntes elétricas têm,
respectivamente, intensidades iA , iB , iC e iD .
a) A corrente elétrica IB é menor, igual ou maior à corrente elétrica iC ? Justifique sua
resposta.
b) Qual é a relação correta entre as correntes elétricas iA , iB e iD ? Justifique sua
resposta.
Página 1 de 13
PROJETO ESPECÍFICAS - UERJ
c) O potencial elétrico no ponto A é menor, igual ou maior ao potencial elétrico no
ponto C? Justifique sua resposta.
3) Um estudante montou o circuito da figura com três lâmpadas idênticas, A, B e C, e
uma bateria de 12V. As lâmpadas têm resistência de 100.
a) Calcule a corrente elétrica que atravessa cada uma das lâmpadas.
b) Calcule as potências dissipadas nas lâmpadas A e B e identifique o que acontecerá
com seus respectivos brilhos (aumenta, diminui ou permanece o mesmo) se a lâmpada
C
queimar.
4) Uma esfera condutora descarregada (potencial elétrico nulo), de raio R1  5,0 cm ,
isolada, encontra-se distante de outra esfera condutora, de raio R2  10,0 cm , carregada
com carga elétrica Q  3,0μC (potencial elétrico não nulo), também isolada.
Em seguida, liga-se uma esfera à outra, por meio de um fio condutor longo, até que se
estabeleça o equilíbrio eletrostático entre elas. Nesse processo, a carga elétrica total é
conservada e o potencial elétrico em cada condutor esférico isolado descrito pela
q
r
equação V  k , onde k é a constante de Coulomb, q é a sua carga elétrica e r o seu
raio.
Página 2 de 13
PROJETO ESPECÍFICAS - UERJ
Supondo que nenhuma carga elétrica se acumule no fio condutor, determine a carga
elétrica final em cada uma das esferas.
5) Um espectrômetro de massa é um aparelho que separa íons de acordo com a razão
carga elétrica/massa de cada íon. A figura mostra uma das versões possíveis de um
espectrômetro de massa. Os íons emergentes do seletor de velocidades entram no
espectrômetro com uma velocidade v . No interior do espectrômetro existe um campo
magnético uniforme (na figura é representado por Be e aponta para dentro da página  )
que deflete os íons em uma trajetória circular. Íons com diferentes razões carga
elétrica/massa descrevem trajetórias com raios R diferentes e, consequentemente,
atingem pontos diferentes (ponto P) no painel detector. Para selecionar uma velocidade
v desejada
e para que o íon percorra uma trajetória retilínea no seletor de velocidades,
sem ser desviado pelo campo magnético do seletor (na figura é representado por e
aponta para dentro da página  ), é necessário também um campo elétrico ( Es ), que não
está mostrado na figura. O ajuste dos sentidos e módulos dos campos elétrico e
magnético no seletor de velocidades permite não só manter o íon em trajetória retilínea
no seletor, como também escolher o módulo da velocidade v . De acordo com a figura e
os dados a seguir, qual o sentido do campo elétrico no seletor e o módulo da velocidade
v
do íon indicado?
Dados: • Es = 2 500 V/m
• Bs = 5,0 x 10–2 T
Página 3 de 13
PROJETO ESPECÍFICAS - UERJ
6) Em um seletor de cargas, uma partícula de massa m e eletrizada com carga q é
abandonada em repouso em um ponto P, entre as placas paralelas de um capacitor
polarizado com um campo elétrico E. A partícula sofre deflexão em sua trajetória
devido à ação simultânea do campo gravitacional e do campo elétrico e deixa o
capacitor em um ponto Q, como registrado na figura.
Deduza a razão q/m, em termos do campo E e das distâncias d e h.
7) Nos pontos A, B e C de uma circunferência de raio 3 cm, fixam-se cargas elétricas
puntiformes de valores 2 μC, 6 μC e 2 μC respectivamente. Determine:
a) A intensidade do vetor campo elétrico resultante no centro do círculo.
b) O potencial elétrico no centro do círculo. (Considere as cargas no vácuo, onde k = 9
× 109 N.m2/C2)
Página 4 de 13
PROJETO ESPECÍFICAS - UERJ
8) Um filtro de velocidades é um dispositivo que utiliza campo elétrico uniforme E
perpendicular ao campo magnético uniforme B (campos cruzados), para selecionar
partículas carregadas com determinadas velocidades. A figura a seguir mostra uma
região do espaço em vácuo entre as placas planas e paralelas de um capacitor.
Perpendicular ao campo produzido pelas placas, está o campo magnético uniforme.
Uma partícula positiva de carga q move-se na direção z com velocidade constante v
(conforme a figura 1).
a) na figura 2, represente os vetores força elétrica, F e, e força magnética, F m, que
atuam na partícula assim que entra na região de campos cruzados, indicando suas
magnitudes.
b) Determine a velocidade que a partícula deve ter, para não ser desviada.
9) Um satélite geoestacionário, portanto com período igual a um dia, descreve ao redor
da Terra uma trajetória circular de raio R. Um outro satélite, também em órbita da
Terra, descreve trajetória circular de raio R/2.
Calcule o período desse segundo satélite.
Página 5 de 13
PROJETO ESPECÍFICAS - UERJ
10) Duas partículas com carga 5 x 10-6 C cada uma estão separadas por uma distância
de 1 m.
Dado K = 9 x 109 Nm2/C2, determine
a) a intensidade da força elétrica entre as partículas.
b) o campo elétrico no ponto médio entre as partículas.
11) Uma onda eletromagnética atinge uma antena no instante em que um elétron nela
se move com velocidade v . As direções e os sentidos da velocidade v do elétron e dos
campos elétrico (E) e magnético (B) da onda, no ponto em que o elétron se encontra
nesse instante, estão indicados na figura a seguir com relação a um sistema de eixos
cartesianos xyz.
 
 
a) Determine as direções e os sentidos das forças elétrica Fe e magnética Fm sobre o
elétron nesse instante.
b) Sabendo que v  1,0  106 m / s, E  3,0  102 V / m e B  1,0  106 T , calcule a
 
 
razão Fe / Fm entre os módulos das forças elétrica Fe e magnética Fm .
12) Um elétron (módulo da carga = q, massa = m) que se move na direção horizontal
penetra entre duas placas paralelas carregadas, como mostra a figura. Entre as placas
existe um campo elétrico uniforme, de módulo E.
Página 6 de 13
PROJETO ESPECÍFICAS - UERJ
a) INDIQUE a expressão algébrica para o cálculo do módulo da força elétrica que atua
sobre o elétron em termos de q e de E.
b) O campo elétrico é tal que a ação da gravidade sobre o elétron é desprezível. As
placas têm um comprimento ℓ e o elétron emerge delas a uma altura h acima da
horizontal. DEMONSTRE que o módulo da velocidade do elétron, quando penetrou
entre as placas, é dado por v = ℓ
qE
2mh
c) Com a aplicação de um campo magnético de módulo B, perpendicular a v , o elétron
passa entre as placas sem sofrer nenhum desvio. INDIQUE, na figura, a direção e o
sentido do vetor B e CALCULE seu módulo em termos de q, de m, de E, de ℓ e de h.
Página 7 de 13
PROJETO ESPECÍFICAS - UERJ
Gabarito:
Resposta da questão 1:
a) Aplicando a lei de Coulomb aos pontos mostrados no gráfico:
F
kQ
2
d2
F
9  10
3
2

kQ
F 

 0,3 2


2

kQ
3
9  10 

 0,12
 0,12

 0,3 2

F
9  10
3


F
9  103

kQ
2
 0,3 2

 0,12
kQ
2

1

9
F  1 103 N.
b) Aplicando novamente a lei de Coulomb:
F
kQ
2
2
 kQ
2
 F d2 
Q d
d
Q  0,1
9  103
9
9  10
F
k

 0,1 106 
Q  1 104 C.
Resposta da questão 2:
O esquema a seguir ilustra a situação:
a) Os pontos B e C estão no mesmo fio, portanto, por eles passa a mesma corrente:
Página 8 de 13
PROJETO ESPECÍFICAS - UERJ
iB = iC = i.
b) Como as duas lâmpadas estão em paralelo e têm resistências iguais, elas são
percorridas por correntes iguais. Então:
iB = iD = i.
Essas duas correntes, iB e iD, somam-se formando a corrente iA. Assim:
iA = iB + iD = i + i  iA = 2 i.
.
Portanto, a relação correta é:
iB  iD 
iA
.
2
c) A diferença de potencial elétrico entre dois pontos é U = R i. Como entre os pontos
citados, A e C, não há elemento resistivo algum, o potencial elétrico no ponto A é igual
ao potencial elétrico no ponto C.
Resposta da questão 3:
a) Dados: U = 12 V; R = 100 .
A resistência equivalente do circuito é:
Req  100 
100
2
 Req  150 Ω.
Aplicando a lei de Ohm-Pouillet:
URI  I
eq
12
150
 I  0,08 A.
Assim:
iA  I  0,08 A;


I
iB  iC   0,04 A.

2
b) Calculemos as potências dissipadas para o caso do item anterior:
2
PR i
P  100  0,08 2  0,64 W;
 A

2

PB  PC  100  0,04   0,16 W.
Se a lâmpada C queimar, as lâmpadas A e B ficam em série, submetidas à tensão U’ = 6
V cada uma.
As novas potências dissipadas serão:
Página 9 de 13
PROJETO ESPECÍFICAS - UERJ
2
P
U'
R
 PA'  PB' 
62
 0,36 W.
100
Comparando os valores obtidos, concluímos que o brilho da lâmpada A diminui e o
brilho da lâmpada B aumenta.
Resposta da questão 4:
Após o contato, as esferas terão o mesmo potencial elétrico.
V1  V2 
kQ1 kQ2
Q
R
5
1

 1  1 
  Q2  2Q1 (01)
R1
R2
Q2 R2 10 2
A carga total não muda, portanto: Q1  Q2  3 (02)
Q1  1μC
Q2  2μC
Substituindo 01 em 02, vem: Q1  2Q1  3  3Q1  3  
Resposta da questão 5:
Se ao entrar no espectrômetro o íon é desviado para cima, aplicando a regra da mão
direita, concluímos tratar-se de um íon positivo.
No Seletor esse íon tem trajetória retilínea. Assim, a força magnética, que é para cima,
deve ser equilibrada pela força elétrica, que, então, é dirigida para baixo.
Página 10 de 13
PROJETO ESPECÍFICAS - UERJ
Se o íon é positivo a força elétrica tem o mesmo sentido do campo elétrico.
Conclusão: o campo elétrico Es é para baixo, conforme indicado na figura.
Calculando v:
Dados: Es = 2.500 V/m; Bs = 5  10–2 T.
E
B
Fmag = Felet  | q | v B | q | E  v = 
2.500
5  102
 v = 5  104 m/s.
Resposta da questão 6:
q/m =
 g . d
E . h 
Resposta da questão 7:
a) O campo elétrico total será a soma vetorial dos campos de cada uma das cargas.
Como as cargas em A e C têm o mesmo valor e estão simetricamente dispostas em
relação ao centro O, produzirão neste ponto campos elétricos de mesmo módulo, porém
de sentidos contrários.
Assim, estes dois campos se anularão, restando apenas o campo de B, cujo módulo é
E
kQB 9x109  6  106

 6,0  107 N / C
2
2
R2
3  10


b) O potencial no centro é a soma algébrica dos potenciais criados pelas três cargas:
V  VA  VB  VC 
K  QA  QB  QC 
R

9  109  10  106
 3,0  106 V
2
3  10
Página 11 de 13
PROJETO ESPECÍFICAS - UERJ
Resposta da questão 8:
a)
b) v = E/B
Resposta da questão 9:
6 2 h.
Resposta da questão 10:
a) A figura mostra as forças de interação entre as duas cargas.
Página 12 de 13
PROJETO ESPECÍFICAS - UERJ
F
k Q1 . Q2
d2

9  109  5  10 6  5  10 6
 0,225N
12
b) A figura mostra os campos gerados pelas cargas no ponto médio.
Como as cargas tem o mesmo valor e as distâncias ao ponto médio são iguais os
campos tem a mesma intensidade. O campo resultante é nulo.
Resposta da questão 11:
a) F e terá a mesma direção que o campo E, mas sentido oposto, isto é: direção do eixo
OZ com sentido negativo. Fm tem a direção do eixo OY e aponta no sentido positivo
do eixo.
b) Fe / Fm  3,0  102
Resposta da questão 12:
a) F = q.E
b) horizontal: ℓ = v.t
vertical: h =
v = ℓ.
1
a.t2 = q.E.t2/2.m
2
 q.E / 2.m.h
c) perpendicular à folha; para dentro da mesma; B =
1
 2.m.h.E / q
Página 13 de 13