Thesis - Técnico Lisboa

Universidade Técnica de Lisboa
Instituto Superior Técnico
Single-Stage Converter for Life Support Appliances
Colwyn Mundell de Calado
Dissertação para obtenção do Grau de Mestre em
Engenharia Electrotécnica e de Computadores
Júri
Presidente:
Prof. Doutor Paulo José da Costa Branco
Orientador:
Prof. Doutor José Fernando Alves da Silva
Vogal:
Prof. Doutor João José Esteves Santana
Setembro 2010
i
Agradecimentos
Agradeço a todos os professores que me ajudaram a completar o curso, pela motivação e
conhecimento transmitido. Um especial agradecimento ao meu orientador, Prof. José Fernando Alves
da Silva, por todo o apoio e disponibilidade na realização deste trabalho.
Agradeço à minha família todo o apoio, compreensão e incentivo demonstrado. Uma palavra
de apreço a todos os meus colegas e amigos que me acompanharam ao longo do percurso
académico.
ii
Resumo
Actualmente, os pacemakers apresentam restrições em relação ao tempo de vida das
baterias, responsáveis por sustentar energeticamente esses aparelhos, facto que é condicionante da
qualidade de vida dos pacientes.
Neste trabalho propõe-se, como alternativa às baterias, a utilização de um microgerador
electromagnético capaz de produzir energia eléctrica a partir dos movimentos respiratórios, com o
objectivo de prolongar o tempo de vida dos aparelhos ou até de evitar a necessidade de substituição
dos mesmos.
Começa-se por estudar o funcionamento do microgerador, determinando-se os parâmetros do
seu modelo matemático e simulando o seu funcionamento.
De seguida, para efectuar a ligação entre o gerador e o pacemaker, são apresentadas duas
soluções de conversores. A primeira solução utiliza um rectificador elevador de duplo estágio de
conversão composto por um rectificador a díodos e por um conversor CC-CC do tipo elevador. A
segunda solução utiliza um rectificador elevador de um único estágio de conversão em que os
transístores utilizados são MOSFETs. Estuda-se o funcionamento dos dois conversores apresentados,
dimensionam-se os seus componentes e simula-se o funcionamento de cada conversor.
Cada solução integra um supercondensador com o objectivo de armazenar a energia eléctrica
que irá alimentar o pacemaker nos períodos em que o gerador não fornece energia.
Finalmente, conclui-se que o conversor de estágio único é a solução mais adequada,
nomeadamente por apresentar um rendimento bastante mais elevado, necessitar de menos tempo
para armazenar a energia necessária para alimentar o pacemaker durante um dia e ocupar menos
volume.
Palavras Chave
Microgerador
Conversor CC-CC elevador
Rectificador
Supercondensador
Factor de potência unitário
iii
Abstract
Nowadays, pacemakers have limitations in terms of the life of the batteries used to power
them, which in turn restricts the quality of life of the patient.
This work proposes the use of an electromagnetic generator, as an alternative to batteries,
which is capable of producing electric power from respiratory motion, in order to prolong the life of the
pacemaker or avoid the need for its replacement.
It begins by studying the way in which the micro-generator works, determining the parameters
of its mathematical model and simulating its function in order to confirm the model described.
Then, in order to link the generator to the pacemaker, two possible solutions for converters are
put forward. The first solution uses a two-stage boost rectifier comprising a diode rectifier and a DCDC boost converter. The second uses a single-stage boost rectifier which uses MOSFET transistors.
The operation of both converters is studied, the components are dimensioned and the performance of
each converter is simulated.
Each solution integrates a supercapacitor in order to store the electric energy which will power
the pacemaker when the generator is not supplying energy.
Finally, it is concluded that the single-stage converter is the more suitable solution because it
is much more efficient, it needs less time to store sufficient energy to power the pacemaker and it
occupies less space.
Keywords
Micro-generator
DC-DC boost converter
Rectifier
Supercapacitor
Unit power factor
iv
Índice
1. Introdução ............................................................................................................................. 1
1.1. Motivação e objectivos.................................................................................................... 1
1.2. Organização do texto ....................................................................................................... 2
2. Sistemas De Energia Para Pacemakers .............................................................................. 3
3. Microgerador Electromagnético ......................................................................................... 7
3.1. Introdução........................................................................................................................ 7
3.2. Produção de energia eléctrica .......................................................................................... 8
3.3. Modelo matemático ....................................................................................................... 11
3.4. Simulação ...................................................................................................................... 13
4. Conversores......................................................................................................................... 16
4.1. Rectificador elevador de duplo estágio de conversão ................................................... 16
4.1.1. Rectificador monofásico de onda completa ........................................................... 16
4.1.1.1. Princípio de funcionamento ............................................................................ 17
4.1.1.2. Dimensionamento dos díodos ......................................................................... 18
4.1.2. Dimensionamento do supercondensador ................................................................ 18
4.1.3. Conversor CC-CC elevador ................................................................................... 19
4.1.3.1. Princípio de funcionamento ............................................................................ 20
4.1.3.2. Análise do conversor sem perdas .................................................................... 21
4.1.3.3. Análise do conversor com perdas.................................................................... 23
4.1.3.4. Dimensionamento dos componentes do conversor ......................................... 24
4.1.3.5. Comando e controlo não linear do conversor.................................................. 27
4.1.4. Simulação ............................................................................................................... 32
4.1.5. Redimensionamento do Supercondensador ........................................................... 38
4.2. Rectificador elevador de um único estágio de conversão ............................................. 39
4.2.1. Princípio de funcionamento ................................................................................... 39
4.2.2. Análise do conversor sem perdas ........................................................................... 40
4.2.3. Análise do conversor com perdas........................................................................... 45
4.2.4. Dimensionamento dos semicondutores .................................................................. 46
4.2.5. Dimensionamento do supercondensador ................................................................ 48
4.2.6. Comando e controlo não linear do conversor......................................................... 49
4.2.7. Simulação ............................................................................................................... 54
5. Conclusão ............................................................................................................................ 61
6. Bibliografia ......................................................................................................................... 63
Anexo A ................................................................................................................................... 65
Anexo B ................................................................................................................................... 67
v
Lista de Figuras
Figura 2.1 - Densidade de potência ( μW cm3 ) em função do tempo de vida.
Figura 2.2 - Comportamento da tensão aos terminais do microgerador.
Figura 2.3 - Rectificador elevador de duplo estágio de conversão.
Figura 2.4 - Rectificador elevador de um único estágio de conversão.
Figura 3.1 - Corte do migrogerador electromagnético MK3.
Figura 3.2 - Corte transversal dos imãs.
Figura 3.3 - Conversão de energia.
Figura 3.4 - Circuito equivalente do microgerador ligado a uma carga resistiva.
Figura 3.5 - Andamento da fem do microgerador em função do tempo.
Figura 3.6 - Andamento da tensão à saída do microgerador em função do tempo.
Figura 3.7 - Andamento da corrente à saída do microgerador em função do tempo.
Figura 4.1 - Rectificador elevador de duplo estágio de conversão.
Figura 4.2 - Rectificador monofásico de onda completa.
Figura 4.3 - Sentidos das correntes.
Figura 4.4 - Conversor CC-CC do tipo elevador.
Figura 4.5 - Conversor CC-CC elevador com
S1
em condução e
Figura 4.6 - Conversor CC-CC elevador com
S1
ao corte e
S 2 ao corte.
S 2 em condução.
Figura 4.7 - Corrente na bobina L em função do tempo.
Figura 4.8 - Controlador não linear de corrente da bobina L .
Figura 4.9 - Diagrama de blocos do controlador de tensão.
Figura 4.10 - Controlo de tensão com limitador de anti-embalamento.
Figura 4.11 - Evolução da fem e corrente no gerador ao longo do tempo.
Figura 4.12 - Evolução da fem e corrente no gerador no regime permanente.
Figura 4.13 - Evolução da tensão e corrente à entrada do conversor CC-CC.
Figura 4.14 - Evolução da tensão e corrente na carga.
Figura 4.15 - Evolução da tensão e corrente à entrada do conversor CC-CC.
Figura 4.16 - Evolução da tensão e corrente da carga.
Figura 4.17 - Evolução da tensão e corrente da carga.
Figura 4.18 - Rectificador elevador de um único estágio de conversão.
Figura 4.19 - Conversor de único estágio de conversão com
S1 e S 2
em condução.
Figura 4.20 - Conversor de único estágio de conversão com
S1 e S3
em condução.
Figura 4.21 - Conversor de único estágio de conversão com
S2 e S4
em condução.
Figura 4.22 - Corrente na bobina Li em função do tempo.
Figura 4.23 - Esquema do controlador não linear de corrente.
Figura 4.24 - Diagrama de blocos do controlador de tensão.
Figura 4.25 - Controlo de tensão com limitador de anti-embalamento.
vi
Figura 4.26 - Evolução da fem e corrente no gerador.
Figura 4.27 - Evolução da corrente no gerador no inicio do regime permanente.
Figura 4.28 - Evolução da tensão e corrente na carga.
Figura 4.29 - Desfasagem entre a fem e corrente no gerador.
Figura 4.30 - Taxa de distorção harmónica de corrente.
Figura 4.31 - Evolução da fem e corrente no gerador.
Figura 4.32 - Evolução da tensão e corrente na carga.
Figura A.1 - Diagrama de blocos do funcionamento do rectificador elevador de duplo estágio
de conversão.
Figura A.2 - Diagrama de blocos do rectificador elevador de duplo estágio de conversão.
Figura A.3 - Diagrama de blocos do controlador de tensão do conversor CC-CC do tipo
elevador.
Figura A.4 - Diagrama de blocos do controlador de corrente do conversor CC-CC do tipo
elevador.
Figura A.5 - Diagrama de blocos do sinal de comando do conversor CC-CC do tipo elevador.
Figura B.1 - Diagrama de blocos do funcionamento do rectificador elevador de um único
estágio de conversão.
Figura B.2 - Diagrama de blocos do rectificador elevador de um único estágio de conversão.
Figura B.3 - Diagrama de blocos do controlador de tensão do rectificador elevador de um único
estágio de conversão.
Figura B.4 - Diagrama de blocos do controlador de corrente do rectificador elevador de um
único estágio de conversão.
Figura B.5 - Diagrama de blocos do sinal de comando do rectificador elevador de um único
estágio de conversão.
Lista de Tabelas
Tabela 2.1 - Comparação dos geradores.
Tabela 3.1 - Características da carga.
Lista de Abreviaturas
C
- Condensador de saída do conversor CC-CC.
CSC1
- Supercondensador do conversor com dois estágios de conversão.
CSC 2
- Supercondensador do conversor com um estágio de conversão.
vii
d
- Duração do impulso eléctrico gerado pelo pacemaker.
Ec
- Energia diária consumida pelo controlador.
Eg
- Energia mínima disponibilizada pelo gerador durante um dia.
Ei
- Energia diária consumida pelos impulsos eléctricos.
eiL
- Erro entre a corrente de referência e a corrente na bobina L .
eiL
- Erro entre a corrente de referência e a corrente na bobina
Em
- Energia diária consumida pelo microprocessador do pacemaker.
ESC1
- Energia armazenada no supercondensador
i
Li .
CSC1 .
ESC1max - Energia máxima armazenada no supercondensador CSC1 .
ESC min
- Energia mínima armazenada no supercondensador
CSC1 .
Eútil
- Energia útil para alimentar a carga.
fc
- Frequência de comutação dos semicondutores totalmente comandados.
fem
- Força electromotriz.
fi
- Frequência da fem do gerador.
fp
- Factor de potência.
H
- Ganho de realimentação.
id
- Corrente de saída do rectificador do conversor de estágio único.
iD max
- Valor máximo da corrente que percorre no díodo.
iL
- Corrente na bobina L .
iLi
- Corrente na bobina
IL
- Valor médio da corrente na bobina L .
I Lef
- Corrente eficaz na bobina L .
I Li ef
- Corrente eficaz na bobina
Li .
Li .
I Li ef max - Valor máximo da corrente eficaz na bobina Li .
I Lcci ef max - Valor máximo da corrente eficaz na bobina Li com o gerador em curto-circuito.
I Li ef min - Valor mínimo da corrente eficaz na bobina Li .
I Li1ef
- Corrente eficaz da harmónica fundamental na bobina
I L max
- Valor máximo da corrente na bobina L .
viii
Li .
iLref
- Corrente de referência na bobina L .
iLi ref
- Valor de referência para a corrente na bobina
I S max
- Corrente máxima a suportar no semicondutor MOSFET.
I S1
- Corrente média a suportar no semicondutor
S1 .
IS 2
- Corrente média a suportar no semicondutor
S2.
iS 1
- Corrente que atravessa o semicondutor
S1 .
iS 2
- Corrente que atravessa o semicondutor
S2.
iS 3
- Corrente que atravessa o semicondutor
S3.
iS 4
- Corrente que atravessa o semicondutor
S4.
I0
- Corrente média da carga.
Ki
- Constante integral do compensador proporcional-integral.
KiTHD
- Taxa de distorção total da corrente.
Kp
- Constante proporcional do compensador proporcional-integral.
L
- Bobina de entrada do conversor CC-CC.
Li
- Valor da indutância no interior do gerador.
Ne
- Número de espiras da bobina
Ni
- Número de impulsos eléctricos emitidos pelo pacemaker durante um dia.
Pc
- Potência do controlador.
Li .
Li .
PcomTotal - Potência de perdas devido à comutação dos MOSFETs.
PcomM
- Potência de perdas devido à comutação do MOSFET.
PcondTotal - Potência de perdas devido à condução dos MOSFETs.
PcondM
- Potência de perdas devido à condução do MOSFET.
Pg
- Potência média produzida pelo gerador em cada semiciclo respiratório.
Pg max
- Potência máxima produzida pelo gerador.
Pi
- Potência média debitada pela fonte da fem.
Pm
- Potência do microprocessador (pacemaker).
PrL
- Potência de perdas na resistência da bobina L .
PU
- Potência média à entrada do conversor CC-CC.
ix
PWM - Pulse Width Modulation.
P0
- Potência média consumida pela carga.
re
- Resistência dos eléctrodos.
Rext
- Raio externo da bobina
Li .
Rint
- Raio interno da bobina
Li .
rg
- Resistência aplicada aos terminais do gerador.
rL
- Resistência da bobina L .
rLi
- Resistência da bobina
rm
- Resistência equivalente do microprocessador (pacemaker).
rSon
- Resistência do MOSFET.
R0
- Resistência equivalente da carga.
t
- Espessura da bobina
Tc
- Período de comutação dos semicondutores totalmente comandados.
Td
- Constante de tempo que representa o atraso devido ao conversor comutado.
Ti
- Período da fem do gerador.
Tp
- Constante de tempo que representa o pólo do compensador proporcional-integral.
tqoff
- Tempo de estabelecimento das condições do estado de corte.
tqon
- Tempo de estabelecimento das condições do estado de condução.
TZ
- Constante de tempo que representa o zero do compensador.
U
- Tensão no supercondensador
U max
- Tensão máxima no supercondensador
CSC1 .
U min
- Tensão mínima no supercondensador
CSC1 .
VDSS
- Tensão máxima a suportar no semicondutor.
Vf
- Tensão limiar de condução no díodo.
vg
- Tensão instantânea aos terminais do gerador.
Vgefmax
- Máximo valor eficaz da tensão aos terminais do gerador.
vi
- Valor instantâneo da força electromotriz do gerador.
Vief
- Valor eficaz da força electromotriz do gerador.
Li .
Li .
CSC1 .
x
Vief max
- Valor máximo eficaz da força electromotriz do gerador.
Vi max
- Amplitude máxima da força electromotriz do gerador.
vL
- Tensão aos terminais da bobina L .
VL
- Valor médio da tensão aos terminais da bobina L .
vLi
- Tensão aos terminais da bobina
VLi
- Valor médio da tensão aos terminais da bobina
VRRM
- Tensão máxima inversa de pico repetitivo.
Vs
- Tensão aplicada aos terminais do pacemaker.
vS 1
- Tensão aos terminais do semicondutor S1.
vS 2
- Tensão aos terminais do semicondutor S2.
vS 3
- Tensão aos terminais do semicondutor S3.
vS 4
- Tensão aos terminais do semicondutor S4.
V0
- Tensão média aos terminais da carga.
v0ref
- Tensão de referência da carga.

- Factor de ciclo de comutação.

- Função de estado dos semicondutores do conversor CC.
1
- Função de estado dos semicondutores do braço 1 do conversor com um único
Li .
Li .
estágio de conversão.
2
- Função de estado dos semicondutores do braço 2 do conversor com um único
estágio de conversão.
cc
- Rendimento do conversor CC-CC.
total
- Rendimento total do conjunto (gerador e conversor).
iL
- Tremor da corrente na bobina L .
iLi
- Tremor da corrente na bobina

- Erro máximo entre a corrente de referência e a corrente na bobina L .
n
- Frequência natural de um sistema de segunda ordem.

- Factor de amortecimento.
1
- Factor de deslocamento.
Li .
xi
1. Introdução
1.1. Motivação e objectivos
A proposta de dissertação, número 227, Single-Stage Converter for Support Life Appliances,
possibilita uma abordagem ao problema de fornecimento de energia a aplicações de suporte à vida,
mais concretamente do pacemaker, o qual apresenta restrições em relação ao tempo de vida das
baterias, que actualmente ronda os cinco a dez anos, responsáveis por sustentar energeticamente o
referido aparelho.
Este projecto tem como principal objectivo propor alternativas de sistemas de fornecimento de
energia eléctrica aos pacemakers capazes de prolongar o tempo de vida dos aparelhos actuais ou até
evitar a necessidade de substituição dos mesmos. Para o efeito, propõe-se a utilização de um
microgerador capaz de aproveitar, através de um processo mecânico, a energia fornecida pela função
respiratória. O foco deste trabalho será comparar duas soluções que utilizam conversores capazes de
alimentar uma carga continua a partir de uma fonte de tensão alternada.
O microgerador, utilizado como fonte de tensão, produz uma tensão alternada sinusoidal que
é diferente da tensão contínua exigida pela carga (pacemaker). As duas soluções apresentadas
pretendem tornar compatíveis estas duas grandezas.
A primeira solução consiste num rectificador a díodos, utilizado tradicionalmente para obter
uma tensão contínua a partir de uma fonte alternada, em conjunto com um conversor CC-CC do tipo
elevador. Este último é utilizado para elevar o nível de tensão obtido à saída do rectificador ao
requisitado pela carga.
A segunda solução trata-se de um rectificador em que os semicondutores utilizados são
transístores do tipo MOSFET em alternativa ao de díodos e são comandados por modulação de
largura de impulso (PWM) de três níveis, com o intuito de obter uma corrente sinusoidal na fonte
alternada em fase com a tensão da mesma (factor de potência unitário), dispensando a necessidade
de usar um conversor CC-CC uma vez que o próprio modelo garante o nível de tensão necessário.
Para uma optimização das duas topologias de conversores implementadas, tendo sempre
presente a questão do volume, procurou-se maximizar o rendimento do gerador e do conversor,
minimizar o número de componentes que constituem o conversor, dimensionar os elementos
reactivos, os semicondutores e os parâmetros dos controladores de tensão e de corrente para que a
resposta dinâmica do sistema seja rápida e eficaz.
Considera-se que a análise e o desenvolvimento de modelos teóricos baseados em
simulações poderão ter um valioso complemento quando testados ou aplicados sobre situações reais,
permitindo, inclusive, concluir sobre a fiabilidade do próprio modelo.
Actualmente, devido às capacidades de cálculo dos computadores que se encontram em forte
desenvolvimento, a simulação de modelos pode ser realizada com considerável detalhe. A
possibilidade de recorrer a programas informáticos, neste caso o Matlab/Simulink, traduz-se numa
1
poderosa ferramenta que permite um elevado número de simulações para obtenção de resultados
que facilita e enriquece o trabalho.
É essencial desenvolver um estudo aprofundado de todos os modelos adoptados para que o
resultado possa ter alguma precisão e consistência, tendo em consideração as limitações dos
programas utilizados e obviamente dos próprios modelos teóricos que apenas são uma tentativa de
representar situações reais. Procurou-se ao longo do projecto mencionar e justificar todas as opções
apresentadas com o maior rigor possível para uma maior precisão e consistência dos modelos
implementados.
1.2. Organização do texto
O relatório encontra-se estruturado em seis capítulos, nos quais se descreve a evolução do
trabalho.
No capítulo 1 faz-se uma breve introdução ao tema e ao objectivo do trabalho.
No capítulo 2 são retratados os problemas associados aos pacemakers artificiais utilizados
actualmente e as bases de construção dos modelos de geradores e conversores.
No capítulo 3 descreve-se, em detalhe, o modelo utilizado para a representação do
microgerador electromagnético. É também neste capítulo que se procede à determinação dos
parâmetros do modelo matemático do microgerador.
O capítulo 4 apresenta a topologia dos conversores bem como o seu funcionamento e
dimensionamento dos componentes constituintes dos mesmos e dos controladores utilizados no
desenvolvimento do projecto. Neste capítulo também é feita uma análise detalhada dos resultados
obtidos por simulação com recurso ao Matlab/Simulink das duas topologias adoptadas.
Nos capítulos 5 e 6, encontram-se as conclusões finais referentes ao trabalho desenvolvido e
a bibliografia, respectivamente.
2
2. Sistemas De Energia Para Pacemakers
Antes de prosseguir com o estudo incluído no âmbito deste projecto, é necessário esclarecer
o que é um pacemaker artificial. Trata-se de um dispositivo electrónico utilizado no tratamento da
arritmia cardíaca. Quando o número de batimentos cardíacos num determinado intervalo de tempo
estiver abaixo do normal, os estímulos eléctricos provenientes do aparelho são disparados para o
interior do coração, de forma a estimular o músculo do coração a um ritmo desejado. O aparelho é
implantado no corpo do paciente [1].
O pacemaker tradicional é alimentado por uma bateria e é constituído por um dispositivo
electrónico (microprocessador) que controla a taxa de impulsos eléctricos e por um ou dois eléctrodos
que transportam o estímulo eléctrico emitido pelo dispositivo ao coração. Os pacemakers
convencionais usam uma bateria de células de iodeto de lítio com elevada densidade de energia. No
entanto, estas baterias têm um tempo de vida limitado, tipicamente, entre 5 e 10 anos, dependendo
do tipo de problema do coração [2]. Embora as baterias nucleares apresentem uma densidade de
energia bastante elevada, são altamente tóxicas e, por razões de segurança, não são utilizadas nos
dispositivos médicos implantáveis [3].
A substituição das baterias exige intervenções cirúrgicas, que por vezes causam algum
desconforto e preocupação aos pacientes, uma vez que, para além do custo, existem alguns riscos
associados a essas intervenções.
A Figura 2.1 mostra uma comparação da densidade de potência versus tempo de vida útil
para células solares, geradores baseados em vibrações mecânicas e vários tipos de baterias
químicas. O limite superior do regime solar representa a potência disponível pelo sol ao meio-dia,
enquanto que o limite inferior está relacionado com a iluminação normal no interior de um escritório.
Em relação aos geradores baseados em vibrações mecânicas, o limite superior caracteriza as
vibrações captadas nas tubulações de uma construção e o limite inferior corresponde a pequenas
vibrações presentes no interior da casa [4].
3
Figura 2.1 - Densidade de potência ( μW cm ) em função do tempo de vida.
3
Esta Figura 2.1 mostra que, para um tempo de vida útil superior a 3 anos, as aplicações de
sistemas de micro-conversão de energia solar e mecânica vibracional são as melhores opções.
O aproveitamento de energia solar através das células fotovoltaicas tem despertado muito
interesse ao mundo actual. Estas células produzem energia eléctrica de forma limpa e fácil e são
utilizadas para alimentar uma grande diversidade de equipamentos eléctricos, desde pequenos
dispositivos como relógios até às grandes máquinas industriais. Os grandes problemas das células
fotovoltaicas existentes no mercado são o baixo rendimento de conversão de energia (na ordem dos
16%) e o elevado custo do material [5]. Obviamente, estas células não podem ser implantadas no
corpo humano, pois devem ser utilizadas em locais onde se podem captar luz para produzirem
energia eléctrica.
Actualmente, um grande número de investigações tem conduzido para o desenvolvimento de
métodos e sistemas para a geração de energia eléctrica a partir das vibrações mecânicas. Em termos
de fenómenos físicos, existem três tipos de transdutores: piezoeléctrico, electrostático e
electromagnético. A Tabela 2.1 mostra alguns geradores e respectivas características mais
relevantes para cada tipo de transdutor [6][7].
Tabela 2.1 - Comparação dos geradores.
Gerador
Tipo
Frequência ( Hz )
Aceleração ( m.s-2 )
Volume ( cm3 )
Potência ( μW )
Vibes MK3
Electromagnético
50
0.6
0.8
58
Vibes MK2
Electromagnético
52
0.6
0.15
46
Perpetuum
Electromagnético
100
0.4
30
4000
Roundy
Piezoeléctrico
120
2.5
1
375
Despesse
Electrostático
50
8.8
1.8
1052
A escolha adequada do tipo de transdutor depende, certamente, do tipo de aplicação
desejada. Por exemplo, os transdutores electrostáticos são mais facilmente integrados nos
dispositivos microelectrónicos, no entanto requerem uma fonte de tensão externa. Os transdutores
piezoeléctricos podem gerar tensões contínuas ou alternadas, ao contrário dos transdutores
electromagnéticos que só permitem gerar tensões alternadas tipicamente inferiores a 1V de amplitude
[8].
O microgerador MK3 é um modelo desenvolvido do microgerador MK2 para alimentar
sensores com tensões e potências semelhantes às requeridas pelos pacemakers. Embora o
microgerador MK2 apresente um volume inferior ao do microgerador MK3, o seu nível de tensão é
demasiado baixo para o fim pretendido. Por esta razão e também devido ao seu baixo volume em
comparação com outros geradores electromagnéticos, decidiu-se utilizar o microgerador MK3 neste
trabalho. A constituição bem como o funcionamento deste microgerador são apresentados no capítulo
3.
4
No estudo a realizar, assume-se que a tensão do microgerador MK3 tem um comportamento
idêntico ao do microgerador MK2 apresentado na Figura 2.2 [6], sendo inclusive de esperar que para
a mesma aceleração, o decréscimo da amplitude do microgerador MK3 seja menos acentuado, em
virtude da sua massa ser maior do que a do microgerador MK2.
Figura 2.2 - Comportamento da tensão aos terminais do microgerador.
No caso representado na Figura 2.2, o microgerador foi sujeito a uma vibração mecânica,
com uma aceleração de 0.6 m.s2 , durante um segundo, verificando-se que após a suspensão
dessas vibrações, a amplitude da tensão gerada vai decrescendo ao longo de vários segundos até se
anular. No caso do microgerador MK3, a amplitude máxima da tensão é de 1.32 V e produz uma
potência máxima de 58 μW sobre uma carga resistiva de 15 kΩ .
Tendo em consideração que o microgerador MK3 gera uma tensão alternada sinusoidal,
enquanto que o pacemaker exige uma tensão contínua, torna-se necessário utilizar um conversor de
modo a compatibilizar a tensão gerada com o tipo de tensão exigida pelo pacemaker. No estudo
desenvolvido são utilizadas duas topologias de conversores distintas.
A primeira topologia, apresentada na Figura 2.3, é constituída por um rectificador a díodos e
por um conversor CC-CC para controlar a tensão da carga. A função deste rectificador é obter uma
tensão contínua a partir de uma fonte de tensão alternada, usando-se, na sua saída, um condensador
para alisar a tensão. No caso deste trabalho, utilizar-se-á um supercondensador em vez de um
condensador comum, pois permitirá armazenar maiores quantidades de energia e, assim, garantir-se
uma maior autonomia para alimentar a carga quando o gerador não está a produzir energia. O
conversor CC-CC a usar neste trabalho será do tipo elevador, pois será necessário elevar a tensão
obtida na saída do rectificador para o nível de tensão da carga (pacemaker). A tensão da carga é
regulada através de um controlador que basicamente permite controlar o factor de ciclo de comutação,
isto é, controla a relação entre os tempos de condução/corte dos semicondutores do conversor CCCC em cada período de comutação. Este tipo de rectificador é designado de conversor de grupo 1, ou
seja, com dois andares de conversão [10].
5
Figura 2.3 - Rectificador elevador de duplo estágio de conversão.
A segunda topologia, apresentada na Figura 2.4, é constituída apenas por um rectificador
com semicondutores totalmente comandados, permite integrar as funções da topologia anterior em
apenas um único estágio de conversão. Os semicondutores são comandados por modulação de
largura de impulso (PWM) de três níveis para se obter uma corrente quase sinusoidal e em fase com
a tensão no gerador. Este tipo de rectificador é designado por conversor de grupo 2, ou seja, com um
andar de conversão [10]. À semelhança da topologia anterior é também usado um supercondensador
na saída do rectificador.
Figura 2.4 - Rectificador elevador de um único estágio de conversão.
6
3. Microgerador Electromagnético
3.1. Introdução
O microgerador Mk3 permite transformar a energia das vibrações mecânicas presentes no
ambiente de aplicação em energia eléctrica. Trata-se de um microgerador electromagnético com
componentes discretos fabricados em miniaturas e optimizados para um nível baixo de vibração
ambiental.
As vibrações mais apropriadas para este gerador podem ser encontradas em inúmeras
aplicações tais como bens de agregado familiar comuns (microondas, refrigeradores, máquinas de
lavar roupa), veículos (automóveis, aviões), equipamentos industriais, estruturas tais como edifícios e
pontes, etc. No entanto, as aplicações baseadas no movimento do corpo humano são caracterizadas
pela baixa frequência e elevada amplitude de deslocamento [6].
Figura 3.1 - Corte do migrogerador electromagnético MK3.
O microgerador usa quatro ímanes de neodímio-ferro-boro ( NdFeB ) de alta densidade
energética colados nas superfícies superior e inferior da viga cantilever. Entre os ímanes existe uma
ranhura na viga cantilever para fixar a bobina como mostra nas Figuras 3.1 e 3.2 [6][9]. O circuito
magnético é completado com barras de aço (ferromagnético) revestidas de zinco para fechar o fluxo
entre as partes superior e inferior dos ímanes. Esta disposição produz um gradiente de fluxo
concentrado através da bobina estacionária à medida que os ímanes vibram.
7
Figura 3.2 - Corte transversal do gerador.
As massas de tungsténio são anexas às extremidades dos ímanes, fornecendo assim uma
massa inercial compacta uma vez que a densidade de tungsténio ( 18.1 g.cm3 ) é superior à dos
ímanes ( 7.6 g.cm3 ). A viga cantilever foi colocada no topo da base através de um parafuso e uma
porca que se encontra na parte inferior da base.
A bobina tem um raio externo de 1.4 mm, um raio interno de 0.25 mm e uma espessura de
0.5 mm . Um fio de cobre com diâmetro 12 μm é usado para formar uma bobina de 2800 espiras ,
com uma resistência total de 2.3 kΩ .
O material da viga cantilever é feito de cobre-berílio ( BeCu ), que possui uma elevada
resistência à fadiga [9].
3.2. Produção de energia eléctrica
O desenvolvimento dos microgeradores electromagnéticos para a produção de energia
eléctrica resultante da conversão dos movimentos do corpo humano como andar, dançar, trabalhar e
outras actividades físicas foi pouco estudado. No trabalho de pesquisa efectuado, não foi encontrado
nenhum artigo detalhado sobre o uso de microgeradores electromagnéticos em humanos.
O microgerador não fornece energia suficiente para alimentar o pacemaker apenas com base
nos movimentos do corpo humano, pois a frequência de ressonância do gerador é muito maior do
que a frequência típica do corpo humano. A transformação de energia mecânica presente nos
movimentos dos órgãos no corpo humano, tais como o movimento torácico, a contracção e expansão
dos pulmões e o movimento do diafragma, para a geração de energia eléctrica do microgerador pode
ser realizada de várias maneiras através de um processo mecânico. Um exemplo simples é mostrado
na Figura 3.3 [11], em que o sistema consiste num tipo de cabine que tem no seu interior um gerador
fixo na parte superior e uma esfera colocada na base, sendo esta movimentada de um lado para
outro por influência do campo gravitacional e dos movimentos respiratórios. Durante a expansão dos
8
pulmões, a cabine é inclinada para um dos lados fazendo com que a esfera seja deslocada para a
extremidade oposta da cabine sob influência do campo gravitacional. Durante a contracção dos
pulmões o processo é revertido.
Figura 3.3 - Conversão de energia.
Portanto, em cada ciclo respiratório, a viga cantilever do microgerador é deflectida duas vezes
devido ao contacto com a esfera. A deflexão máxima da viga cantilever é ajustada tendo em
consideração que o microgerador gera uma tensão máxima de 931 mV sobre uma carga resistiva de
15 kΩ. A frequência respiratória numa pessoa adulta em repouso é de 16 ciclos por minuto [12],
significando isso que em cada semiciclo respiratório terá uma duração aproximada de 2 segundos.
Com base na Figura 2.2, em cada semiciclo respiratório (2 s), a potência média produzida
pelo gerador é aproximadamente:
2s
Pg 

0
V
gef max
 1/ 3Vgefmax  t 
rg
2s
 dt
2

2
Vgef
max
2rg

Pg max
2
 29 μW
Portanto, o gerador produz uma potência média igual à metade da potência máxima.
Geralmente, as pessoas dormem entre 6 e 9 horas por dia. Durante este período o microgerador não
produz energia eléctrica, pois a pessoa não se encontra na posição vertical e por esse motivo o
movimento da esfera não é efectuado da forma prevista para esta posição. Na situação mais
desfavorável, o microgerador produzirá energia durante 15 horas por dia, ou seja, a energia mínima
disponibilizada pelo gerador durante um dia será:
Eg  Pg 15h  1566 mJ
Este valor não corresponde à situação real do trabalho, apenas tem como objectivo
dimensionar o consumo do pacemaker e do controlador que regula a tensão de saída do conversor.
9
A energia diária consumida pelo pacemaker é composta por duas componentes: a energia
diária consumida devido aos impulsos eléctricos e a energia diária consumida pelo microprocessador
que controla a taxa de impulsos e são dadas por, respectivamente [13] [14]:
Ei 
Vs2  d
 Ni [J]
re
 3.1
Em 
Vs2
.86400 [J]
rm
 3.2
Onde Vs é a tensão aplicada aos terminais do pacemaker, re é a resistência entre os
eléctrodos, d é a duração do impulso eléctrico, N i é o número de impulsos eléctricos emitidos por
dia e rm é a resistência equivalente do microprocessador.
Um pacemaker típico pode conter as seguintes características [14]:

Taxas de impulsos: 70 batimentos por minuto;

Duração do impulso: 0.5 ms;

Resistência entre os eléctrodos: 750 kΩ.
A energia diária consumida devido aos impulsos eléctricos é máxima quando o valor de N i é
máximo, ou seja, 100.800 impulsos por dia. Considera-se que o microprocessador do pacemaker tem
uma resistência equivalente de 2.2 MΩ (valor típico), com uma tensão mínima aplicada de 1.8 V
(incluí uma margem de segurança, isto é, o pacemaker pode funcionar um pouco abaixo desse valor).
Assumindo que a tensão de saída do conversor não excede 2.2 V, então a energia máxima
consumida em cada componente do pacemaker será:
Ei  325.3 mJ
Em  190 mJ
O microgerador vai alimentar uma carga total, composta por três cargas distintas: a carga dos
eléctrodos, a carga do microprocessador e a carga do controlador. Considerando que a energia
máxima consumida na carga durante um dia é de 70% da energia mínima diária disponível pelo
microgerador calculada anteriormente, então a energia diária consumida pelo controlador é:
Ec  0.70Eg -  Ei  Em   580 mJ
A Tabela 3.1 ilustra as características da carga necessárias para o dimensionamento dos
conversores electrónicos de potência.
10
Tabela 3.1 - Características da carga.
Dispositivo
Resistência
Eléctrodos
750 
Microprocessador
Controlador
2.2 M
720 K
Corrente
Potência
Consumo diário
2.93 mA @ 2.2 V
6.45 mW @ 2.2 V
325 mJ @ 2.2 V *
2.4 mA @ 1.8 V
4.32 mW @ 1.8 V
218 mJ @ 1.8 V *
1 μA @ 2.2 V
2.2 μW @ 2.2 V
190 mJ @ 2.2 V
0.82 μA @ 1.8 V
1.47 μW @ 1.8 V
127 mJ @ 1.8 V
3.05 μA @ 2.2 V
6.71 μW @ 2.2 V
580 mJ @ 2.2 V
2.5 μA @ 1.8 V
4.5 μW @ 1.8 V
389 mJ @ 1.8 V
1095 mJ @ 2.2 V
Total
734 mJ @ 1.8 V
* Energia máxima.
3.3. Modelo matemático
O fluxo magnético gerado em torno da bobina resultante das vibrações dos ímanes induz uma
tensão na bobina chamada força electromotriz (fem). Quando o microgerador electromagnético está
ligado a uma carga resistiva, o sistema eléctrico envolvido pode ser aproximado por um circuito RL da
primeira ordem com a indutância da bobina ( Li ) em série com a resistência da carga ( rg ) e com a
resistência da bobina ( rLi ). O esquema eléctrico equivalente deste circuito está representado na
Figura 3.4 [15].
Figura 3.4 - Circuito equivalente do microgerador ligado a uma carga resistiva.
11
A força electromotriz do microgerador electromagnético, representada por vi , pode ser
determinada aplicando a regra de divisor de tensão:
vi 
rg  rLi
rg
vg
 3.3
Com base nos dados enunciados na secção 3.2, é possível determinar o valor máximo eficaz
da fem, Vief , sendo este de 1.075 V. O valor máximo da corrente eficaz fornecida pelo microgerador
será:
I Li efmax 
Vgefmax
rg
 62 μA
Quando o microgerador está em curto-circuito, neste caso o valor máximo da corrente eficaz
será:
I Lcci ef max 
Vief max
rLi
 467 μA
A fórmula de Wheeler permite calcular com precisão (na gama de microhenry a algumas
dezenas de milihenrys) o valor da indutância da bobina Li . A fórmula de Wheeler, para dimensões
em centímetros, é a seguinte [16]:
 R  Rext 
2
0.315   int
  Ne
2


Li 
[μH]
 Rint  Rext 
6
  9   Rext  Rint   10  t
2


2
3.4 
Em que Rint e Rext são os raios interno e externo da bobina, respectivamente, t é a
espessura da bobina e N e é o número de espiras. De acordo com os dados mencionados na secção
3.1, a indutância da bobina que constitui o microgerador é de 8.28 mH.
12
3.4. Simulação
O funcionamento do microgerador foi simulado no programa Matlab/Simulink, para analisar o
comportamento das grandezas eléctricas apresentadas na secção do modelo matemático. Aos
terminais do microgerador aplica-se uma carga de 15 kΩ com o objectivo de confirmar se a tensão
máxima à saída do microgerador é de 931 mV .
A Figura 3.5 demonstra o comportamento similar da fem do microgerador durante um ciclo
respiratório, bem como a sua forma de onda.
Figura 3.5 - Andamento da fem do microgerador em função do tempo.
Observa-se que a fem tem a forma de onda de uma sinusóide, com uma amplitude inicial de
1.52 V. Ao longo do semiciclo respiratório a sua amplitude decresce gradualmente até atingir uma
amplitude de 0.51 V.
A evolução no tempo da tensão e corrente na carga estão representadas nas Figuras 3.6 e
3.7, respectivamente.
13
Figura 3.6 - Andamento da tensão à saída do microgerador em função do tempo.
Figura 3.7 - Andamento da corrente à saída do microgerador em função do tempo.
14
Dado tratar-se de uma carga resistiva, seria de esperar que a forma de onda das grandezas
eléctricas de carga fosse idêntica à da fem do microgerador. Nas simulações realizadas, verifica-se
que os valores máximos eficazes da tensão e corrente na carga são 931 mV e 62 μA,
respectivamente. Conclui-se que os resultados obtidos na simulação estão de acordo com os valores
teóricos, desta forma o modelo matemático do microgerador é válido aproximadamente e será
utilizado na simulação para o funcionamento dos conversores.
15
4. Conversores
4.1. Rectificador elevador de duplo estágio de conversão
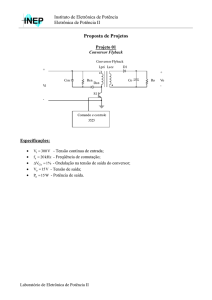
A topologia do rectificador elevador de duplo estágio de conversão, representada na Figura
4.1, é composta por um rectificador monofásico de onda completa seguido de um conversor CC-CC
do tipo elevador. A tensão alternada do gerador é rectificada através do rectificador para se obter na
sua saída uma tensão contínua. Na saída do rectificador é utilizado um supercondensador para alisar
a tensão, bem como para armazenar a energia eléctrica que irá alimentar a carga nos períodos em
que o gerador não fornece energia. O conversor CC-CC permite elevar a tensão obtida na saída do
rectificador para o nível de tensão da carga (pacemaker). A tensão da carga é regulada, através do
controlador, para o valor mínimo exigido pelo pacemaker (1.8 V). Para o estudo e para o
dimensionamento dos componentes do conversor e dos parâmetros do controlador, despreza-se a
carga dos eléctrodos dado que esta depende do estado do coração.
Figura 4.1 - Rectificador elevador de duplo estágio de conversão.
4.1.1. Rectificador monofásico de onda completa
O rectificador monofásico de onda completa, representado na Figura 4.2, tem como função
obter uma tensão contínua a partir de uma fonte de tensão alternada.
16
Figura 4.2 - Rectificador monofásico de onda completa.
4.1.1.1. Princípio de funcionamento
Nas alternâncias positivas da corrente na fonte de tensão alternada, os díodos D1 e D3
conduzem pois estes encontram-se polarizados directamente, enquanto que os díodos D2 e D4 se
encontram inversamente polarizados, ou seja, não conduzem. Durante as alternâncias negativas,
verifica-se o caso oposto, ficando os díodos D2 e D4 polarizados directamente, enquanto que os
díodos D1 e D3 se encontram polarizados inversamente. A Figura 4.3 ilustra os sentidos das
correntes para cada um dos casos.
(a) iLi  0
(b) iLi  0
Figura 4.3 - Sentidos das correntes.
17
Em ambos os casos, a passagem de corrente na carga é realizada no mesmo sentido e
portanto a tensão aos terminais da carga mantém sempre a mesma polaridade.
4.1.1.2. Dimensionamento dos díodos
Os díodos mais utilizados para a rectificação dos sinais são os díodos de silício, os díodos de
germânio e os díodos de schottky. Os díodos de silício são mais económicos e robustos e são muito
utilizados em aplicações industriais que envolvem potências mais elevadas. Embora os díodos de
germânio tenham uma tensão limiar de condução mais baixa, geralmente os díodos de schottky são
mais adequados para a rectificação de potências mais baixas devido ao baixo valor de corrente
reversa.
Desprezando as potências dissipadas no rectificador e no interior do gerador, os valores
máximos de tensão inversa e corrente que os díodos deverão suportar são os seguintes:
VRRM   2Vief max  1.52 V
I D max  2I Lcci efmax  660 μA
O díodo schottky SS0520 da PANJIT tem um bom compromisso para a solução, porque a
tensão limiar de condução é baixa ( Vf =0.17 V@If =10 mA ) e a corrente reversa ( Ir <0.1 μA ) é
desprezável face à corrente consumida na carga. Para o estudo assume-se que a tensão limiar de
condução é constante e igual a 0.17 V.
4.1.2. Dimensionamento do supercondensador
O supercondensador que será utilizado na saída do rectificador é um tipo de condensador
que é capaz de armazenar grandes quantidades de energia eléctrica por unidade de tamanho quando
comparado a condensadores comuns. Os supercondensadores apresentam várias vantagens em
relação às baterias recarregáveis tais como ciclos de carga-descarga ilimitados, rendimento muito
elevado e baixa toxicidade de materiais usados. No entanto, a sua densidade de energia armazenada,
quando comparada com as baterias, é significativamente mais baixa. Se desprezarem as perdas
devido à resistência interna do gerador, o valor máximo da tensão no supercondensador será:
U max  Vi max  2V f  1.18 V
Onde V f é a tensão limiar de condução no díodo.
18
A energia eléctrica armazenada no supercondensador é dada por:
1
ESC1  CSC1U 2
2
 4.1
Onde CSC1 é a capacidade do supercondensador, expressa em faraday, e U é a tensão aos
terminais do supercondensador.
Para garantir que a energia eléctrica armazenada no supercondensador esteja sempre
disponível, este deve ter capacidade para armazenar energia capaz de alimentar a carga durante 24
horas (embora 9 horas possa ser suficiente em situações normais). A corrente à entrada do conversor
CC-CC estará limitada a 20 μA , portanto para fornecer potência suficiente à carga considera-se que
a tensão mínima do supercondensador é de 0.5 V. Desprezando as perdas de potência no conversor
CC-CC elevador, da equação (4.1) pode-se escrever:
Eútil  ESC1max  ESC1min  CSC1 U max 2  U min 2   CSC1 
2  Eútil
U max 2  U min 2 
 4.2 
Sabendo que a energia útil ( Eútil ) necessária para alimentar a carga durante um dia é de 734
mJ (ver Tabela 3.1), então o valor mínimo da capacidade do supercondensador deverá ser:
CSC1 
2  Eútil
2  734 103

 1.28 F
2
2
 U min
U max
 1.182  0.52 
4.1.3. Conversor CC-CC elevador
O conversor CC-CC do tipo elevador é um tipo de conversor de contínuo para contínuo que
permite obter na sua saída uma tensão maior do que a tensão de entrada. Este tipo de conversor
está representado na Figura 4.4 [17].
19
Figura 4.4 - Conversor CC-CC do tipo elevador.
4.1.3.1. Princípio de funcionamento
À entrada do conversor elevador está ligado a um supercondensador, SC1, que se comporta
como uma fonte de tensão contínua de valor U praticamente constante em cada período do gerador.
Os semicondutores S1 e S2 são comutados alternadamente e periodicamente através de um
controlador, sendo a frequência de comutação fc  1 Tc , onde Tc é o período de comutação dos
semicondutores.
Designa-se por factor de ciclo de comutação,  , a porção do período de comutação em que o
semicondutor S1 conduz. Em cada período de comutação, no intervalo 0  t   Tc o semicondutor S1
está em condução, enquanto que o semicondutor S2 está ao corte, transferindo energia da fonte
contínua para a bobina L . Durante o restante período 1    Tc , o semicondutor S2 entra em
condução, enquanto que o semicondutor S1 é posto ao corte, transferindo energia da bobina L ao
condensador e à carga. Os semicondutores S1 e S2 não podem conduzir simultaneamente, pois
originaria um curto-circuito no condensador.
20
4.1.3.2. Análise do conversor sem perdas
Na análise do conversor sem perdas, os semicondutores comportam-se como interruptores
ideais e apresentam dois estados de funcionamento: corte e condução. Seja
 a variável que
representa o estado de cada semicondutor:

 0  S1 em condução e S2 ao corte  0  t   Tc 

 1  S1 ao corte e S2 em condução  Tc  t  Tc 
 
 4.3
No modo de funcionamento   0 , a corrente da fonte vai apenas percorrer a bobina L para
que esta armazene energia eléctrica, enquanto que o condensador C descarrega na resistência R0 . A
Figura 4.5 ilustra esta situação.
Figura 4.5 - Conversor CC-CC elevador com S1 em condução e S 2 ao corte.
Com base no esquema da Figura 4.5, podem deduzir-se as seguintes expressões:
 vL  U
 v 0
 S 1
vS 2  V 0
 i i
 S1 L
 iS 2  0
21
 4.4
No modo de funcionamento γ=1 , a corrente na bobina decresce uma vez que a tensão vL é
negativa, o que faz com que a energia armazenada nesta bobina seja transferida para o condensador
e para a carga. A Figura 4.6 ilustra esta situação.
Figura 4.6 - Conversor CC-CC elevador com S1 ao corte e S 2 em condução.
Com base nas malhas representadas na Figura 4.6, deduzem-se as seguintes expressões:
vL  U  V0
 v V
0
 S 1
 vS 2  0
 i 0
 S1
 iS 2  iL
 4.5
Portanto, a evolução da tensão aos terminais da bobina L é representada por:
 U
vL  t   
 U  V0
se   0  0  t   T 
se   1  T  t  T 
22
 4.6
Em regime permanente, o valor médio da tensão aos terminais da bobina é nulo, obtendo-se
dessa condição o factor de ciclo do conversor:
VL 
T
1  T
U
U
U  dt   U  V0  dt   0 
 1-     1 


T

T  0
V0
V0
 4.7 
A resistência equivalente da carga total pode ser calculada por:
V0 2
V0 2
R0 
=
P0 Pc  Pm
(4.8)
Onde Pc e Pm são as potências consumidas pela carga do controlador (conversor) e do
microprocessador (pacemaker), respectivamente.
4.1.3.3. Análise do conversor com perdas
Admitindo agora a existência de perdas no conversor, estas são contabilizadas como perdas
na resistência da bobina L ( rL ) para além das perdas associadas à comutação e condução dos
semicondutores. As perdas no condensador são consideradas desprezáveis face às perdas na
bobina L e nos semicondutores.
O rendimento do conversor CC-CC elevador é dado por:
cc 
Pr
P0 V0 I 0 UI L  PrL  PcondTotal  PcomTotal
P
P


=1- L - condTotal - comTotal
PU UI L
UI L
UI L
UI L
UI L
(4.9)
Onde PrL são as perdas na resistência rL , PcondTotal são as perdas totais devido à condução
dos semicondutores e PcomTotal são as perdas totais devido à comutação dos semicondutores. Estas
perdas podem ser calculadas através das equações que se seguem [17] [18]:
2
PrL  rL I Lef
 4.10
PcondTotal  PcondM  rSon I L2
(4.11)
PcomTotal  2  PcomM  2  V0 I L
23
t
qon
 tqoff 
2
fc
(4.12)
Onde rSon é a resistência interna de condução, tqon é o tempo de estabelecimento das
condições do estado de condução e tqoff é o tempo de estabelecimento das condições do estado de
corte.
Da expressão (4.9), pode-se calcular o valor médio da corrente na bobina L :
IL 
V0 I 0
P
 0
ccU ccU
(4.13)
4.1.3.4. Dimensionamento dos componentes do conversor
A tensão nominal à entrada do conversor será de 1.18 V e a tensão de saída será fixada no
valor de 1.8 V, correspondente à tensão mínima de operação do pacemaker. A corrente à entrada do
conversor estará limitada a um valor de 20 μA para evitar grandes perdas de potência no regime
transitório. Em regime permanente, considera-se um rendimento do conversor CC-CC de 96%.
Os valores da corrente média na bobina L e da resistência equivalente de carga podem ser
obtidos tendo em conta os valores da Tabela 3.1:
IL 
P0
P P
 c m  5.27 μA
ccU
ccU
R0 
V02
V02

 542.7 kΩ
P0 Pc  Pm
Elementos reactivos
O dimensionamento dos elementos reactivos do conversor CC-CC deverá ser feito tendo em
conta o tamanho dos componentes reactivos, as variações máximas admissíveis da corrente na
bobina L e da tensão no condensador C .
A equação diferencial que descreve o comportamento da corrente na bobina L ao longo do
tempo é dada por:
VL  L
24
diL
dt
 4.14
Para pequenas variações de corrente e em regime permanente, a expressão (4.14) pode ser
linearizada como:
VL  L
iL
t
 4.15
Quando o conversor entra no modo de funcionamento   0 , a corrente na bobina L cresce
( iL  0 ) durante o intervalo t   T como mostra na Figura 4.7. Da equação (4.6) vem:
L U
T
iL
 4.16
Figura 4.7 - Corrente na bobina L em função do tempo.
Manipulando as equações (4.7) e (4.16), tira-se que:
L  1   V0
T
iL

V0
  2 

iL f c
 4.17 
Derivando a equação (4.17) em ordem a  e igualando a zero, obtém-se a expressão do
coeficiente de auto-indução da bobina L na situação mais desfavorável:
V0
dL
 0  1- 2  0    0.5  Lmax 
d
4iL f c
25
 4.18 
Atendendo à expressão (4.7), verifica-se que o valor do factor de ciclo obtido para a situação
mais desfavorável está dentro dos limites estabelecidos:
 min  1 
U max
U
 0.35 e  max  1  min  0.72
V0
V0
Assume-se que, em regime permanente, a corrente na bobina L apresente um tremor de
20% em torno do seu valor médio ( iL  0.2I L ), do qual garante regime não lacunar ( I L  iL 2 ).
Assume-se que a frequência máxima de comutação é de 150 MHz, da equação (4.18) determina-se o
valor necessário do coeficiente de auto-indução da bobina L :
L  2.85 mH
Assumindo que a potência dissipada na resistência da bobina L representa 0.5% da potência
debitada pela fonte de fem, então esta resistência pode ser calculada através da expressão (4.10):
rL 
PrL
I
2
Lef

0.005Pi 0.005P0

 1120 
I L2
cc I L2
No cálculo da capacidade do condensador é necessário ter em conta o consumo da carga
dos eléctrodos, para evitar grandes variações de tensão na carga. Durante a emissão do impulso
eléctrico, a carga é praticamente alimentada pelo condensador. Então:
I0 
V0
dv
 C 0
R0
dt
 4.19
Supondo V0 lentamente variável ( V0  V0 ), a sua derivada pode ser aproximada por uma
recta:
I0  C
V0
t
 4.20
Assume-se que a tensão no condensador apenas pode ter uma variação de 1% do seu valor
médio. Como t  d  0.5 ms e I 0  2.4 mA (ver Tabela 3.1), tem-se:
I0  C
V0
I d
 C  0  67 μF  C  100 μF
d
V0
26
O condensador 2.5SZE100M tem uma capacidade de 100 μF e uma resistência de 5 m . As
perdas na resistência do condensador são desprezáveis face às restantes perdas no conversor CCCC elevador.
Semicondutores
A escolha adequada dos semicondutores é essencial para o funcionamento correcto do
conversor comutado. Os semicondutores totalmente comandados vulgarmente mais utilizados nos
conversores de potência são os semicondutores MOSFETs e IGBTs. Optou-se por utilizar os
transistores MOSFETs, pois estes são especialmente utilizados em potências baixas e trabalham em
frequências de comutação muito elevadas, enquanto que os IGBTs são mais adequados em
potências altas e trabalham em frequências mais baixas.
Os valores de tensão e corrente que os semicondutores MOSFETs deverão suportar são os
seguintes:
VDSS  V0  1.8 V
I S max  iL max  20 μA
A estes valores deve ser acrescido um factor de segurança de 100%.
Assume-se que as perdas de condução representam 0.1% das perdas totais e as perdas de
comutação dos semicondutores representam os restantes 3.4%. Com base nas expressões (4.11) e
(4.12), os semicondutores MOSFETs deverão possuir as seguintes características:
rSon 
PcondTotal 0.001P0

 224 Ω
2
I Lef
cc I L2
tqon  tqoff 
PcomTotal 0.034 P0

 0.14 ns
V0 I L f c ccV0 I L f c
4.1.3.5. Comando e controlo não linear do conversor
Os semicondutores do conversor elevador são comandados através de um sistema de
controlo em cadeia fechada que regula o valor médio da corrente na bobina L de modo a que a
tensão de saída cumpra os requisitos exigidos pela carga. Este tipo de controlo designa-se por
27
controlo de tensão de saída ( v0 ) com controlo interno de corrente de entrada ( iL ) e deverá satisfazer
os seguintes objectivos:

Valor médio da tensão na carga igual a 1.8 V;

Corrente máxima na bobina L limitada a 20 μA ;

Tremor de corrente na bobina L aproximadamente 20% do seu valor médio.
Atendendo à expressão (4.6), a tensão aos terminais da bobina L pode ser escrita em
função da variável de comando  , ou seja:
vL  t   1   U   U  V0 
Sabendo que vL  t   L
(4.21)
diL
, a equação (4.21) permite escrever:
dt
L
diL
 1   U   U  V0 
dt
(4.22)
Assim:
diL
 0  iL 
dt
diL
Se   1 
 0  iL 
dt
Se   0 
Como os dispositivos semicondutores são comutados a frequências finitas, existirá um erro
associado à comparação entre a corrente da bobina L e a corrente de referência. Definindo-se este
erro como:
eiL  iLref  iL
(4.23)
Num sistema em modo de deslizamento, verifica-se que o erro varia no intervalo   eiL   .
Para garantir que o sistema permaneça em modo de deslizamento, é necessário cumprir a seguinte
condição de estabilidade [17]:
eiL
deiL
dt
28
0
(4.24)
Deste modo:
eiL    I Lref  I L  I L     0
eiL    I Lref  I L  I L     1
Este controlo pode ser implementado recorrendo ao comparador histerético com largura de
histerese 2 (   iL 2 ). A Figura 4.8 está representada o controlador de corrente implementado
[17].
Figura 4.8 - Controlador não linear de corrente da bobina L .
Uma vez que a corrente na bobina L vai seguir uma referência aproximadamente constante,
a corrente média à saída do conversor CC-CC será proporcional à corrente média da bobina L e
pode considerar-se o seu valor médio igual a GI L . Assim, a equação diferencial que descreve o
comportamento da tensão no condensador ao longo do tempo é:
dv0 ic GI L  I 0
 =
=
dt C
C
GI L 
V0
R0
C
(4.25)
Aplicando a transformada de Laplace à equação (4.25), obtém-se a função de transferência
para a carga:
v0
R0
1


GI L sC  1
sCR0  1
R0
29
(4.26)
Sabendo que em regime permanente o valor médio da corrente no condensador é nulo, então
o valor médio da corrente na carga é I 0  GI L . Através da equação (4.13), tira-se que:
G
ccU
(4.27)
V0
Donde se obtém G  0.629 .
A função de transferência para o conversor com corrente controlada pode ser descrita por:
I0
I Lref

G
G

sTd
e
1  sTd
(4.28)
Onde Td representa o atraso na resposta do conversor e depende do instante de comutação
dos dispositivos semicondutores. Como este atraso é aleatório e pode variar entre 0 e Td , é usual
definir o valor Td igual a metade do período de comutação. No entanto, o conversor é visto como um
sistema de fase não mínima e para melhorar a estabilidade do sistema, assume-se um valor dez
8
vezes superior, ou seja, Td  3.33 10 s .
O compensador do tipo proporcional permite obter uma resposta rápida mas não garante erro
estático nulo, enquanto que o compensador do tipo integral permite garantir erro estático nulo mas a
resposta do sistema é lenta. Assim, para controlar a tensão da carga será utilizado um compensador
do tipo proporcional integral (PI), sendo caracterizado por um pólo na origem e um zero. Este
compensador reúne as duas acções anteriores, ou seja, permite melhorar a velocidade de resposta
do sistema e obter erro estático nulo.
A função de transferência do compensador proporcional integral é dada por:
C s 
Tz s  1
Tp s
(4.29)
Que também pode ser dada por:
C s  K p 
Onde K p 
Tz
1
e Ki  .
Tp
Tp
30
Ki
s
(4.30)
A Figura 4.9 ilustra o diagrama de blocos detalhado do controlador de tensão, com um
limitador de corrente e um ganho H=0.5 na realimentação [17].
Figura 4.9 - Diagrama de blocos do controlador de tensão.
A função de transferência do sistema pode ser simplificada cancelando o pólo dominante do
sistema através do zero do compensador:
Tz  CR0
(4.31)
Deste modo, obtém-se uma função de transferência em cadeia fechada de segunda ordem
sem zeros para o sistema [17]:
v0
v0 ref
HG
R
TpTd
1

H s 2  1 s  HG R
Td
TpTd
A equação (4.32) pode ser escrita na forma canónica
(4.32)
n2
, donde se obtém um
s 2  2n s  n2
conjunto de duas equações:
 2 HGR
n  T T

p d

 2  1
n

Td
Em que n é a frequência natural do sistema e  é o factor de amortecimento.
31
(4.33)
Especificando o valor de   2 2 , que permite minimizar a sobreelevação e ter uma boa
velocidade de resposta, é possível determinar o valor de Tp :
Tp  2HGR0Td
(4.34)
A partir das expressões (4.31) e (4.34), determinam-se os valores dos ganhos do
compensador proporcional integral:
Kp 
Tz
C

 4.7743 103
Tp 2 HGTd
Ki 
1
1

 87.972
Tp 2 HGR0Td
A análise do controlador que se acaba de fazer é válida para regimes de pequenas
perturbações. Em regimes de grandes perturbações, o conversor pode estar sujeito a sobrecorrentes
elevadas devido a grandes variações de carga. Para evitar este problema, será utilizado um
compensador PI com limitador de anti-embalamento apresentado na Figura 4.10, com Kw=1/Kp [17].
Figura 4.10 - Controlo de tensão com limitador de anti-embalamento.
4.1.4. Simulação
Com base nas expressões obtidas anteriormente, pode-se implementar, recorrendo ao
software Matlab/Simulink, um diagrama de blocos representativo do funcionamento do rectificador
elevador de duplo estágio de conversão. O diagrama de blocos utilizado pode ser visualizado no
anexo A.
32
Um dos principais objectivos da simulação é verificar se o controlo de tensão está a funcionar
correctamente e se é estável, isto é, se a tensão aos terminais do condensador C em regime
permanente é igual à tensão de referência ( v0 ref  1.8 V ) e se a corrente na bobina L segue uma
referência constante com um tremor de aproximadamente 20% do valor médio.
Devido
às
capacidades
de
cálculo
do
computador,
considerou-se
o
valor
do
supercondensador igual a 500 μF , com uma tensão inicial de 0.5 V e a tensão inicial do condensador
de 1.7 V. As simulações realizadas estão apresentadas nas Figuras 4.11, 4.12, 4.13 e 4.14.
Figura 4.11 - Evolução da fem e corrente no gerador ao longo do tempo.
33
Figura 4.12 - Evolução da fem e corrente no gerador no regime permanente.
Figura 4.13 - Evolução da tensão e corrente à entrada do conversor CC-CC.
34
Figura 4.14 - Evolução da tensão e corrente na carga.
Da Figura 4.12, no que respeita à corrente na entrada do rectificador, esta tem a forma de
impulsos arredondados cuja amplitude diminui com a diminuição da amplitude da tensão do gerador
até a corrente se anular. A corrente tem esta forma de onda pois o rectificador tem à sua saída um
supercondensador (alisamento da tensão), que carrega quando a sua tensão é inferior à tensão de
saída do gerador subtraída da queda de tensão do rectificador (de duas quedas de tensão
provocadas pelos díodos). Na Figura 4.11, verifica-se que o pico máximo da corrente em cada
período do semiciclo respiratório decresce ligeiramente ao longo do tempo, porque a tensão no
supercondensador aumenta gradualmente ao longo do tempo até atingir o regime permanente.
Utilizando as ferramentas do Matlab, calculou-se a potência média útil à saída do rectificador durante
o regime transitório inicial até que a tensão média do supercondensador atinja 0.7 V (valor máximo
que se irá admitir para o redimensionamento do supercondensador), tendo sido obtido o valor de
12.98 μW . Portanto, o número de horas necessário de funcionamento para garantir a alimentação da
carga durante um dia é de 16 horas ( t  E P ).
Da Figura 4.13, verifica-se que o valor médio da tensão no supercondensador em regime
permanente é de 0.8 V. Este valor é bastante inferior ao valor de pico máximo da fem devido às
perdas associadas à resistência da bobina Li e às duas quedas de tensão provocadas pelos díodos
do rectificador e também devido ao facto da potência fornecida pelo gerador ser insuficiente para que
a tensão no supercondensador atinja o seu valor máximo posível quando o pico da tensão do gerador
é máximo.
35
Observa-se na Figura 4.13 que o valor médio da corrente na bobina L do conversor é de
7.6 μA , com um tremor próximo de 23% do valor médio da corrente. O rendimento do conversor CCCC é aproximadamente 98% ( cc  P0 I LU ). Este valor é ligeiramente superior ao valor previsto
teoricamente, porque na simulação não tem em conta as perdas de comutação dos semicondutores.
Como se pode observar na Figura 4.14 a tensão na carga apresenta um valor médio em
regime permanente de 1.8 V, no qual se conclui que o controlador do conversor está a funcionar
correctactamente.
O rendimento total do conjunto, gerador e conversor, em regime permanente pode ser
calculado através da relação entre a potência média debitada pela fonte de fem e a potência média
consumida pela carga durante o semiciclo respiratório:
total
1 T
P0 T 0 v0i0 dt
 
Pi 1 T v i dt
i Li
T 0
(4.35)
Utilizando as ferramentas do Matblab, o rendimento obtido na simulação foi de 57%.
Assume-se agora que o pacemaker gera impulsos eléctricos frequentemente após o regime
permanente. As simulações realizadas estão apresentadas nas Figuras 4.15, 4.16 e 4.17.
Figura 4.15 - Evolução da tensão e corrente à entrada do conversor CC-CC.
36
Figura 4.16 - Evolução da tensão e corrente da carga.
Figura 4.17 - Evolução da tensão e corrente da carga.
37
Na Figura 4.15 observa-se que a tensão no supercondensador desce ligeiramente para o
valor de 0.7 V, pois a potência média consumida na carga é maior.
Como se pode observar na Figura 4.16, a tensão na carga apresenta um valor médio em
regime permanente de 1.8 V, pelo que se conclui que o controlador do conversor é estável para
regime de grandes perturbações.
Na Figura 4.17, verifica-se uma leigeira redução da tensão na carga devido à passagem da
corrente na carga, mas a sua variação é inferior a 1% do seu valor médio o que está dentro dos
limites pretendidos.
4.1.5. Redimensionamento do Supercondensador
Com base nos resultados obtidos na simulação, pode-se calcular a capacidade do
supercondensador com mais rigor. Tendo em conta o rendimento do conversor CC-CC, o valor da
capacidade do supercondensador necessário é:
CSC1 
2  Eútil
2  734 103

 6.37 F
2
2
cc U max
 U min
 0.96   0.72  0.52 
O supercondensador SC2R7803Z-V de 8 F foi o escolhido por apresentar um volume baixo
3
(1.62 cm ).
38
4.2. Rectificador elevador de um único estágio de conversão
A topologia do rectificador elevador de um único estágio de conversão está representada na
Figura 4.18 [10]. Este tipo de conversor permite integrar as funções do conversor apresentado na
secção 4.1 em apenas um único estágio de conversão. Os semicondutores são comandados por
modulação de largura de impulso (PWM) de três níveis através de um controlador para se obter uma
corrente sinusoidal e em fase com a tensão no gerador. Neste caso, não será necessário introduzir
uma bobina à entrada do rectificador, uma vez que o próprio gerador dispõe de uma. O conversor
utiliza na sua saída um supercondensador para alisar a tensão, bem como para armazenar a energia
eléctrica que irá alimentar a carga nos períodos em que o gerador não fornece energia. No sentido de
minimizar a capacidade do supercondensador, a tensão da carga é regulada para 2.2 V. Para o
estudo e para o dimensionamento dos componentes do conversor e dos parâmetros do controlador,
despreza-se a carga dos eléctrodos dado que esta depende do estado do coração.
Figura 4.18 - Rectificador elevador de um único estágio de conversão.
4.2.1. Princípio de funcionamento
Dada a topologia apresentada na Figura 4.18, os semicondutores de um mesmo braço não
devem conduzir simultaneamente, pois originaria um curto-circuito no condensador.
39
A frequência de comutação dos semicondutores é muito maior do que a frequência do
gerador ( f c  fi ), o que implica que a tensão do gerador é aproximadamente constante em cada
período de comutação.
Quando vi  0 , os semicondutores S1 e S2 são postos em condução no intervalo 0  t   Tc e
a energia da fonte alternada é transferida para a bobina Li . Durante o restante período 1    Tc , os
semicondutores S1 e S3 entram em condução e a energia armazenada na bobina é transferida para a
carga e para o supercondensador.
No caso de vi  0 a situação é idêntica ao do caso anterior, mas como a corrente do gerador
circula no sentido contrário, os semicondutores S2 e S4 são postos em condução em vez dos
semicondutores S1 e S3, para se manter o mesmo sentido da corrente na carga.
4.2.2. Análise do conversor sem perdas
Na análise do conversor sem perdas, os semicondutores comportam-se como interruptores
ideais e apresentam dois estados de funcionamento: corte e condução. As variáveis que caracterizam
o estado dos semicondutores de cada braço são definidos como  1 e  2 :
0
1
1  
S1 ao corte e S4 em condução
S1 em condução e S4 ao corte
0
1
2  
S2 ao corte e S3 em condução
(4.36)
S2 em condução e S3 ao corte
Para uma modulação de largura de impulso a três níveis, seja    1   2 a variável de
comando, que toma os seguintes valores:
 1

  0
 1

se  1  1 e  2  0 S1 e S3 ON 
se  1   2 =1  S1 e S2 ON 
se  1  0 e  2  1 S2 e S4 ON 
(4.37)
No modo de funcionamento   0 , a corrente da fonte vai apenas percorrer a bobina Li ,
fazendo com que esta armazene energia. Se vi  0 , a corrente na bobina Li é positiva e cresce uma
vez que a tensão vLi é positiva. Se vi  0 , a corrente na bobina Li é negativa e cresce em módulo
pois a tensão vLi é negativa. Como o circuito da carga está isolado do circuito da fonte vi , o
supercondensador CSC 2 vai descarregar na resistência da carga. A Figura 4.19 ilustra esta situação.
40
Figura 4.19 - Conversor de único estágio de conversão com S1 e S 2 em condução.
Com base nas malhas representadas na Figura 4.19, deduzem-se as seguintes expressões:
vLi  vi


vg  0

 v v 0
 S 1 S 2
 vS 3  vS 4  V 0
i  i  i
S2
Li
 S1
 iS 3  iS 4  0

id  0

(4.38)
No modo de funcionamento   1 , a tensão vi é positiva e a corrente na bobina Li decresce
uma vez que a tensão aos terminais da bonina é negativa ( vLi  0 ), transferindo a energia
armazenada na bobina Li para o circuito da carga. A Figura 4.20 ilustra esta situação.
41
Figura 4.20 - Conversor de único estágio de conversão com S1 e S3 em condução.
Com base nas malhas representadas na Figura 4.20, deduzem-se as seguintes expressões:
 vLi  vi  V0

 vg  V0
 v v 0
S3
 S 1
v

v
 S2
S4  V 0
 i  i  i
Li
 S1 S 3
 iS 2  iS 4  0

id  iLi

(4.39)
No modo de funcionamento   1 , a tensão vi é negativa bem como a corrente na bobina
que decresce em módulo uma vez que a tensão vLi é positiva. A energia armazenada na bobina Li é
transferida para o supercondensador e para a carga. A Figura 4.21 ilustra esta situação.
42
Figura 4.21 - Conversor de único estágio de conversão com S 2 e S 4 em condução.
Com base nas malhas representadas na Figura 4.21, deduzem-se as seguintes expressões:
 vLi  vi  V0

 vg  V0
v  v  V 0
S1
S3


v

v
 S2
S4  0
 i i 0
 S1 S 3
 iS 2  iS 4  iLi


 id  iLi
(4.40)
Portanto, a evolução da tensão aos terminais da bobina L é representada por:
vi  t   V0  t 

vLi (t )   vi  t 
v  t   V  t 
0
 i
43
se  =1
se  =0
se  =-1
(4.41)
Quando a tensão vi é positiva, a tensão aos terminais da bobina será:
 vi  t 
vLi (t )  
vi  t   V0  t 
se  =0  0  t   Tc 
se  =1  Tc  t  Tc 
(4.42)
Uma vez que a frequência de comutação dos semicondutores é muito maior do que a
frequência da fonte alternada, a tensão vi é aproximadamente constante em cada período de
comutação e, em regime permanente, o valor médio da tensão aos terminais da bobina é nulo. Assim:
VLi 
T
v
v
1  T
vi  dt    vi  V0  dt  =0  i =1-    1  i


T

T  0
V0
V0
 4.43
Como o factor de ciclo está compreendido entre 0 e 1, facilmente verifica-se que a tensão V0
é sempre maior do que a tensão vi .
A resistência equivalente da carga total pode ser calculada por:
V0 2
V0 2
R0 
=
P0 Pc  Pm
(4.44)
Onde Pc e Pm são as potências consumidas pela carga do controlador (conversor) e do
microprocessador (pacemaker), respectivamente.
O factor de potência pode ser expresso como [17]:
fp 
Pi Vief I Li1ef

cos 1 
Si Vief I Li ef
1
K
2
iTHD
1
cos 1
(4.45)
Onde  1 é o factor de deslocamento que corresponde à desfasagem entre a tensão eficaz e
a corrente eficaz da primeira harmónica, e
KiTHD é a taxa de distorção total da corrente que pode ser
obtida através da seguinte expressão:
KiTHD
 I L ef
  i
 I L ef
 i1
44
2

 1


(4.46)
A corrente I Li é composta por duas componentes: a componente da primeira harmónica e a
componente de tremor cuja forma de onda é aproximadamente uma onda triangular de amplitude pico
a pico iLi . Então o valor eficaz da corrente é:
I Li ef  I
2
Li1ef
I
2
Litremor ef
 I
2
Li1ef
 1 iLi 


 3 2 
2
(4.47)
Substituindo a equação (4.47) na equação (4.46), obtém-se:
KiTHD 
iLi
2 3I Li1ef
(4.48)
Para um tremor de 20% do valor eficaz da corrente ( iLi  0.2I Li1ef ), a taxa de distorção da
corrente é cerca de 5.77%.
4.2.3. Análise do conversor com perdas
Admitindo agora a existência de perdas no conversor, estas são contabilizadas como perdas
na resistência da bobina Li ( rLi ) para além das perdas associadas à comutação e condução dos
semicondutores. As perdas no supercondensador são consideradas desprezáveis face às perdas na
bobina Li e nos semicondutores.
O rendimento do conjunto, conversor e gerador, é dado por:

Vief I Li ef  PrL  PcondTotal  PcomTotal
PrL
P0
VI
P
P
i
i
 0 0 
=1- condTotal - comTotal
Pi Vief I Li ef
Vief I Li ef
Vief I Li ef Vief I Li ef Vief I Li ef
(4.49)
Onde PrL são as perdas na resistência rLi , PcondTotal são as perdas totais devido à condução
i
dos semicondutores e PcomTotal são as perdas totais devido à comutação dos semicondutores. Estas
perdas podem ser calculadas através das equações que se seguem:
PrL  rLi I L2i ef
 4.50
PcondTotal  2  PcondM  2  rSon I L2i ef
(4.51)
i
45
PcomTotal  4  PcomM  4  V0 I Li ef
t
qon
 tqoff 
2
fc
(4.52)
Onde rSon é a resistência interna de condução, tqon é o tempo de estabelecimento das
condições do estado de condução e tqoff é o tempo de estabelecimento das condições do estado de
corte.
Da expressão (4.49), pode-se calcular o valor eficaz da corrente na bobina Li :
I Li ef 
V0 I 0
P
 0
Vief Vief
(4.53)
4.2.4. Dimensionamento dos semicondutores
A fem máxima do gerador será de 1.075 V e a tensão da carga será fixada no valor de 2.2 V.
A amplitude da corrente à entrada do conversor estará limitada a um valor de 87.7 μA . Em regime
permanente, considera-se um rendimento do conversor (incluindo o gerador) de 96% quando a
corrente eficaz do gerador é mínima.
Os valores da corrente média na bobina Li e da resistência equivalente de carga podem ser
obtidos tendo em conta os valores da Tabela 3.1:
I Li 
P0
P P
 c m  8.63 μA
ccU
ccU
V02
V02
R0 

 543.2 kΩ
P0 Pc  Pm
Antes de dimensionar os semicondutores é necessário calcular o valor máximo da frequência
de comutação. Sabendo que vLi  diLi dt e linearizando esta equação, tem-se:
VLi  Li
46
iLi
t
(4.54)
Para vi  0 e   0 , a corrente cresce durante o intervalo t   T como mostra na Figura
4.22. Atendendo à expressão (4.41), tem-se:
vi  Li
iLi
T
=Li
iLi f c

Figura 4.22 - Corrente na bobina
 fc =
vi
Li iLi
(4.55)
Li em função do tempo.
Substituindo a equação (4.43) na equação (4.55), obtém-se a expressão da frequência de
comutação em função das tensões vi e V0 :
fc 
V0vi  vi2
V0 iLi Li
(4.56)
Derivando a equação (4.56) em ordem a vi e igualando a zero, obtém-se o valor máximo da
frequência de comutação na situação mais desfavorável:
V0 -2vi =0  vi =
V0
2
 f cmax 
V0max
4iLi Li
(4.57)
Assumindo um tremor de 20% do valor mínimo eficaz para a corrente na bobina Li
( iLi  0.2I Li ef min ), o valor da frequência máxima de comutação será:
fcmax  40 MHz
47
Os valores de corrente e tensão que os semicondutores deverão suportar são os seguintes:
VDSS  V0  2.2 V
I S max  2I Li ef max  87.7 μA
A estes valores deve ser acrescido um factor de segurança de 100%.
Os valores da potência debitada pela fonte de fem do gerador e da potência dissipada na
bobina Li são, respectivamente:
Pi  Vief max I Li ef min  9.28×10-6 μW
PrL  rLi I L2i ef min  0.171 μW
i
Donde se pode concluir que as perdas devido à resistência na bobina Li correspondem a
1.85% das perdas totais. Dos restantes 2.15%, 1.8% representam as perdas totais de comutação dos
semicondutores e 0.35% representam as perdas totais de condução dos semicondutores. Com base
nas expressões (4.51) e (4.52), os semicondutores MOSFETs deverão possuir as seguintes
características:
rSon 
PcondTotal 0.0035P0

 218 Ω
I L2i ef
2cc I L2i ef
tqon  tqoff 
2 PcomTotal
2  0.018P0

 0.11 ns
4V0 I Li ef f c cc  4V0 I Li ef f c
4.2.5. Dimensionamento do supercondensador
A capacidade do supercondensador deve ser dimensionada de modo a garantir que este seja
capaz de armazenar a energia para alimentar a carga durante um dia e a sua tensão possa variar
entre 1.8 V e 2.2 V.
Como a resistência não é constante e a potência varia com a tensão da carga, assume-se
que a energia armazenada necessária no supercondensador é igual à energia máxima diária
consumida pela carga. Deste modo:
CSC 2 
2  Eútil
2 1.095

 1.37 F
2
2
V0max  V0min
2.22  1.82
48
Tendo em conta os valores disponíveis no mercado, o supercondensador SC2R7203Z-V de
2 F e tensão nominal de 2.7 V ocupa o volume de 0.67 cm3, que é inferior ao volume do gerador (0.8
3
cm ).
4.2.6. Comando e controlo não linear do conversor
Tal como no conversor CC-CC da topologia anterior, utilizar-se-á um controlador de tensão de
saída ( v0 ) recorrendo ao controlo interno de corrente de entrada ( iLi ). Neste caso, o sistema de
controlo deve cumprir os seguintes objectivos:

Tensão de carga igual a 2.2 V;

Corrente da bobina Li deve seguir uma referência sinusoidal e em fase com a fem do
gerador, com uma amplitude máxima de 87 μA ;

Variação máxima da corrente na bobina Li inferior a 20% do seu valor eficaz.
Atendendo às expressões (4.38), (4.39) e (4.40), a tensão aos terminais do gerador depende
da variável de comando,  , e pode tomar os seguintes valores:
 V0

vg   0
V
 0
Sabendo que vLi  t   Li
diLi
dt
se  =1
se  =0
se  =-1
, a equação (4.41) permite escrever:
 diLi
   vi  t   V0  t    1    vi  t 
 Li
dt

 L diLi     v  t   V  t   1    v  t 
i

0
i
 i dt
Assim, para vi  0 , tem-se:
Se  =0 
Se  =1 
diLi
dt
diLi
dt
(4.58)
 0  iLi 
 0  iLi 
49
se vi  0    0    1
(4.59)
se vi  0    0    1
Para vi  0 , tem-se:
Se  =0 
Se  =-1 
diLi
dt
diLi
dt
 0  iLi 
 0  iLi 
Definindo o erro associado à comparação entre a corrente da bobina Li e a corrente de
referência como:
eiL  iLi ref  iLi
(4.60)
i
No sistema em modo de deslizamento, o erro varia entre 1  eiL  1 , onde  1 é o erro
i
máximo admissível. O sistema permaneça em modo de deslizamento se satisfazer a seguinte
condição de estabilidade:
eiL
deiL
i
i
dt
0
(4.61)
Deste modo:
eiL  1  I Li ref  I Li  I Li  
eiL  1  I Li ref  I Li  I Li  
diLi
dt
diLi
dt
 0   1  0.5
 0   1  0.5
Para se obter uma modulação de largura de impulso de três níveis, é necessária informação
adicional que garanta que a variável de comando,  , tome os valores da expressão (4.58). Como o
erro de comparação entre as duas correntes é sempre menor ou igual a 21 , utiliza-se um
comparador histerético com largura de histerese 2 2 , maior que 21 , para que este possa tomar um
valor positivo quando a corrente de referência se encontra na alternância positiva e vice-versa, isto é:
eiL   2  I Li ref  0   2  0.5
i
eiL   2  I Li ref  0   2  0.5
i
O erro  1 é igual à metade da variação máxima de corrente na bobina em cada período de
comutação. O erro  2 deve ser maior do que  1 e, neste caso, tomou  2  iLi . O esquema do
controlador de corrente está representado na Figura 4.23.
50
Figura 4.23 - Esquema do controlador não linear de corrente.
Em cada período do gerador, a corrente média à saída do conversor é aproximadamente
proporcional ao valor eficaz da corrente do gerador e pode considerar-se o seu valor médio igual a
GI Li ef . Assim, a equação diferencial que descreve o comportamento da tensão no supercondensador
ao longo do tempo é:
dv0
i
 c =
dt CSC 2
GI Li ef  I 0
CSC 2
GI Li ef 
=
V0
R0
CCS 2
(4.62)
Aplicando a transformada de Laplace à equação (4.62), obtém-se a função de transferência
para a carga:
v0  GI Li1ef
1
 GI1ef
1
sCSC 2 
R0
R0
sCSC 2 R0  1
(4.63)
Sabendo que em regime permanente o valor médio da corrente no condensador é nulo, então
o valor médio da corrente na carga é I 0  GI L . A partir da equação (4.53), tira-se que:
G
Vief
V0
Donde se obtém G  0.469 .
51
(4.64)
A função de transferência para o conversor com corrente controlada pode ser descrita por:
I Li
I Li ref

G
G

sTd
e
1  sTd
(4.65)
O tempo de atraso Td deve ser igual a um quarto do período do gerador para que a corrente
da bobina Li seja quase sinusoidal, ou seja:
Td 
Ti
1

 5 ms
4 4 fi
Tal como no caso do conversor CC-CC, será utilizado um compensador do tipo proporcional
integral para obter erro estático nulo e com uma boa velocidade na resposta dinâmica do sistema. A
Figura 4.24 ilustra o diagrama de blocos global do sistema com ganho de realimentação igual a 0.5.
Figura 4.24 - Diagrama de blocos do controlador de tensão.
A função de transferência do sistema pode ser simplificada cancelando o pólo dominante do
sistema através do zero do compensador:
Tz  CR0
(4.66)
Deste modo, obtém-se a função de transferência em cadeia fechada de segunda ordem sem
zeros para o sistema [17]:
v0
v0 ref
HG
R0
TpTd
1

H s 2  1 s  HG R
0
Td
TpTd
52
(4.67)
A equação (4.67) pode ser escrita na forma canónica
n2
, donde se obtém um
s 2  2n s  n2
conjunto de duas equações:
 2 HGR
n  T T

p d

 2  1
n

Td
(4.68)
Em que n é a frequência natural do sistema e  é o factor de amortecimento.
Especificando o valor de   2 2 , que permite minimizar a sobreelevação e ter uma boa
velocidade de resposta, tem-se:
Tp  2HGR0Td
(4.69)
Utilizando as expressões (4.66) e (4.69), calcula-se os ganhos do compensador proporcionalintegral:
Kp 
Tz
C

 8.5288 102
Tp 2 HGTd
Ki 
1
1

 7.8505 104
Tp 2 HGR0Td
À semelhança do conversor CC-CC é também usado um compensador PI com limitador de
anti-embalamento. A saída deste compensador é multiplicada por uma onda sinusoidal com
amplitude unitária, como mostra na Figura 4.25, para que a corrente de referência tenha a forma de
onda sinusoidal e em fase com a fem do gerador.
53
Figura 4.25 - Controlo de tensão com limitador de anti-embalamento.
4.2.7. Simulação
Recorreu-se ao software Matlab/Simulink para simular o funcionamento do rectificador
elevador de um único estágio de conversão, a fim de verificar se o controlo de tensão está a funcionar
correctamente, ou seja, se a tensão aos terminais do supercondensador em regime permanente é
igual à tensão de referência (2.2 V) e se a corrente à entrada do rectificador tem a forma de uma
sinusoide e em fase com a fem do gerador. O diagrama de blocos correspontente a este conversor
está visualizado no anexo B.
Devido
às
capacidades
de
cálculo
do
computador,
considerou-se
o
valor
do
supercondensador igual ao do condensador do conversor CC-CC, ou seja, 100 μF e a sua tensão
inicial será de 1.8 V. As simulações realizadas estão apresentadas nas Figuras 4.26, 4.27, 4.28, 4.29
e 4.30.
54
Figura 4.26 - Evolução da fem e corrente no gerador.
Figura 4.27 - Evolução da corrente no gerador no inicio do regime permanente.
55
Figura 4.28 - Evolução da tensão e corrente na carga.
56
Figura 4.29 - Desfasagem entre a fem e corrente no gerador.
Figura 4.30 - Taxa de distorção harmónica de corrente.
57
Na Figura 4.26 observa-se que a corrente no gerador tem a forma de onda quase sinusoidal e
em fase com a tensão, tal como seria de esperar. No regime transitório inicial, a amplitude da
corrente é constante e igual ao valor máximo definido pelo controlo de tensão, permitindo assim
entregar toda a energia possível da fonte à carga e ao supercondensador, exceptuando as perdas
dissipadas no conversor e na bobina do próprio gerador. Na eminência de atingir o regime
permanente, a amplitude da corrente decresce gradualmente para evitar sobre-elevação na tensão da
carga, como mostra na Figura 4.27. Após o regime permanente, a amplitude da corrente no gerador
aumenta com a diminuição da amplitude da tensão para que a potência média entregue à carga em
cada período da fonte alternada seja mantida constante. Utilizando as ferramentas do Matlab,
calculou-se a potência média útil entregue à carga no primeiro semiciclo respiratório (regime
transitório inicial), tendo sido obtido o valor de 34.5 μW . Portanto, o número de horas necessário de
funcionamento para garantir a alimentação da carga durante um dia é de apenas 9 horas ( t  E P ).
Por observação da Figura 4.28, verifica-se que a tensão na carga apresenta um valor
constante de 2.2V, no qual se conclui que o controlador de tensão está a funcionar de forma correcta.
Na Figura 4.29, verifica-se que a desfasagem entre a tensão e corrente no gerador está
próximo de 0.1 ms. Sabendo que o período da tensão e corrente é de 20 ms, pode-se calcular a
desfasagem em graus:
1 
0.1 ms  3600
 1.80
20 ms
Pela Figura 4.30, verifica-se que, para a pior situação, ou seja, quando a corrente eficaz é
mínima, a taxa de distorção harmónica de corrente no gerador é de 5.78% o que está de acordo com
o valor previsto teoricamente.
Assim, é possível calcular o valor do factor de potência através da equação (4.45), sendo este
de 0.998.
Com base na expressão (4.35), o rendimento total do conversor (incluindo o gerador) em
regime permanente é de 91%.
Assume-se agora que o pacemaker gera impulsos eléctricos frequentemente após o regime
permanente. As simulações realizadas estão apresentadas nas Figuras 4.31 e 4.32.
58
Figura 4.31 - Evolução da fem e corrente no gerador.
Figura 4.32 - Evolução da tensão e corrente na carga.
59
Na Figura 4.32 verifica-se que durante a emissão do impulso eléctrico, a tensão da carga
decresce ligeiramente devido à queda de tensão provocada pela passagem da corrente na carga. Na
Figura 4.31 verifica-se que após a emissão do impulso eléctrico a amplitude da corrente no gerador
está no seu valor máximo de forma a carregar o supercondensador o mais rápido possível, até que a
tensão da carga atinja o valor de referência (2.2 V).
60
5. Conclusão
Como foi referido no capítulo 1, a motivação deste trabalho surge dos problemas relacionados
com o fornecimento de energia eléctrica ao pacemaker, o qual apresenta restrições em relação ao
tempo de vida das baterias, condicionando desta forma a qualidade de vida dos pacientes.
No sentido de minorar tais problemas, investigaram-se alternativas de geração de energia
eléctrica que permitissem prolongar o tempo de vida dos aparelhos ou até evitar a necessidade de
substituição dos mesmos. No capítulo 2 foram apresentados vários tipos de geradores com elevada
densidade de energia, concluindo-se que o microgerador electromagnético MK3 era o mais
apropriado para alimentar o pacemaker devido ao seu tamanho reduzido e à sua capacidade para
fornecer a energia necessária ao seu funcionamento.
No capítulo 3 apresenta a constituição e o funcionamento do microgerador electromagnético
MK3. Conforme foi referido o gerador pode produzir uma potência de 58 μW e uma tensão de 931
mV. Verificou-se que não era possível o gerador MK3 fornecer energia directamente a partir dos
movimentos do corpo humano, porque a frequência típica do corpo humano não coincide com a
frequência de ressonância do microgerador. Para resolver este problema, foi apresentado um método
que possibilita transformar a energia proveniente dos movimentos respiratórios em energia eléctrica
através de um processo mecânico. Estimou-se que o gerador, funcionando 15 horas por dia, seria
capaz de disponibilizar diariamente uma energia de 1566 mJ sobre uma carga resistiva de 15 kΩ .
Este valor represente 150% da energia máxima consumida pelo pacemaker e pelo controlador
durante um dia. O funcionamento do microgerador foi simulado com recurso ao programa do Matlab,
confirmando-se que os resultados obtidos na simulação estão de acordo com os valores teóricos.
Para efectuar a ligação entre o microgerador e o pacemaker, foram apresentadas, no capítulo
4, duas soluções de conversores. A primeira solução utiliza um rectificador elevador de duplo estágio
de conversão composto por um rectificador a díodos e por um conversor cc-cc do tipo elevador. A
segunda solução utiliza um rectificador elevador de um único estágio de conversão em que os
transístores utilizados são MOSFETs.
Na simulação realizada para o caso do rectificador elevador de duplo estágio de conversão,
constatou-se que:
i.
a corrente do gerador tinha a forma de impulsos arredondados, porque o
supercondensador apenas carregava quando a sua tensão era inferior à tensão do
gerador subtraída da queda de tensão do rectificador. Em consequência disso, a
tensão máxima obtida no supercondensador foi de apenas 0.8 V que é muito inferior
ao valor máximo de pico da fem do gerador (1.52 V);
ii.
o valor médio da tensão na carga era igual ao valor de referência (1.8 V), concluindose que o controlador de tensão do conversor CC-CC funcionava correctamente;
iii.
em regime permanente a corrente à entrada do conversor CC-CC apresentava um
valor médio de 7.6 μA , com um tremor ligeiramente superior aos limites definidos;
61
iv.
o conversor CC-CC do tipo elevador apresenta um rendimento próximo de 98%,
enquanto que o conjunto (gerador, rectificador e conversor CC-CC) apresenta um
rendimento de 57%, sendo o rectificador o principal responsável por este valor baixo;
v.
a potência média útil à saída do rectificador é de 13 μW , necessitando-se de 16
horas de funcionamento para garantir a alimentação da carga durante um dia;
vi.
na situação em que o pacemaker emite impulsos eléctricos com frequência, regista
uma ligeira flutuação na tensão da carga com uma variação inferior a 1% do seu valor
médio e a tensão no supercondensador desceu para aproximadamente 0.7 V.
Na simulação realizada para o caso do rectificador elevador de um único estágio de
conversão constatou-se que:
i.
a corrente no gerador,
sem considerar a geração de impulsos eléctricos do
pacemaker, tinha a forma de uma onda quase sinusoidal (THD=5.78%) e que se
encontrava praticamente em fase com a tensão, determinando-se um factor de
potência de 0.998;
ii.
o valor médio da tensão na carga era igual ao valor de referência (2.2 V), concluindose que o controlador de tensão funcionava correctamente;
iii.
em regime permanente o conjunto, gerador e conversor, apresenta um rendimento
elevado - 91%;
vii.
a potência média útil fornecida à carga é de 34 μW , necessitando-se de apenas 9
horas de funcionamento para garantir a alimentação da carga durante um dia;
iv.
na situação em que o pacemaker emite impulsos eléctricos com frequência, apenas
se regista uma ligeira flutuação na tensão da carga, sem qualquer relevância para o
funcionamento do modelo.
Do dimensionamento dos componentes, pode concluir-se que o volume da topologia que
utiliza o conversor de um único estágio de conversão é significativamente menor do que a topologia
que utiliza o conversor de duplo estágio de conversão, pois o volume do supercondensador é
3
3
bastante menor (0.67 cm face a 1.62 cm ), utiliza menos semicondutores e menos componentes
reactivos.
Conclui-se, claramente, que o conversor de estágio único é a solução mais adequada,
nomeadamente por apresentar um rendimento mais elevado, necessitar de menos tempo para
armazenar a energia necessária para alimentar o pacemaker durante um dia e ocupar menos volume.
62
6. Bibliografia
[1]
http://pt.wikipedia.org/wiki/Marcapasso , 22-06-2010
[2]
http://www.cardioassoc.com/patient_pgs/procedures/pacemaker.asp, 22-06-2010
[3]
V.S. Mallela, V. Ilankumaran, N.S. Rai, Trends in Cardiac Pacemaker Batteries, Indian Pacing
and Electrophysiology Journal, vol4, nº4, pp. 201-212, 2004.
[4]
Shad Roundy, Brian P. Otis, Yuen-Hui Chee, Jan M. Rabaey, Paul Wright, A 1.9GHz RF
Transmit Beacon using Environmentally Scavenged Energy, IEEE Symp. on Low Power Elect. And
Dev., 2003.
[5]
http://pt.wikipedia.org/wiki/Célula_fotoelétrica, 22-06-2010
[6]
Beeby S., R N Torah, M J Tudor, P Glynee-Jones, T O’Donnell, C R Saha, S Royl, A Micro
Electromagnetic Generator for Vibration Energy Harvesting, J. Of Micromech. Microeng. 17, 2007, pp.
1257-1265
[7]
S.P. Beeby, R. N. Torah, M.J. Tudor, Kinetic Energy Harvesting, School of Electronics and
Computer Science University of Southampton, UK, 2008.
[8]
Shad Roundy, Eli S. Leland, Jessy Baker, Eric Carleton, Elizabeth Reilly, Elaine Lai, Brian
Otis, Jan M. Rabaey, Paul K. Wright, Improvising Power Output for Vibration-Based Energy
Scavengers, IEEE Pervasive Computing, 2005.
[9]
R. N. Torah, P. Glynne-Jones, M.J. Tudor, S.P. Beeby , Energy aware wireless microsystem
th
powered by vibration energy harvesting, Proc PowerMEMS 2007, 28-29 November, 2007, Freiburg,
Germany, pp. 323-326.
[10]
V. Fernão Pires, J. Fernando Silva, Rectificadores com factor de potência quase unitário.
[11]
Haluk Kulah, Khalil Najafi, Method and micropower generator for generating electrical power
from low frequency vibrational energy, Document Nº: US20080136562, 2008
[12]
Nuno Melo, O Sistema Respiratório, 2007
http://pwp.net.ipl.pt/eselx/nunom/elementos/05_sistema_respiratorio.ppt, 9-08-2010
[13]
Fernando Silveira, Dennis Flandre, Low power analog CMOS for cardiac pacemakers: Design
and Optimization in Bulk and SOI Technologies, Boston, MA: Kluwer Academic Publishers, 2004
63
[14]
Mark W. Sweesy, FHRS, CDDS, CEPS, Fundamental Electrical Relationships: Ohm’s Law,
Strength Duraction Curve & Factors Affecting Thresholds , CardioRhytm 2009.
http://www.cardiorhythm.com/2009/pdf/21/95.pdf, 22-06-2010
[15]
Sergey Y. Yurish, Sensors & Transducers, Volume 103, 2009.
[16]
http://www.sabereletronica.com.br/secoes/leitura/113, 22-06-2010
[17]
J. F. Alves da Silva, Sistemas de Energia em telecomunicações: Texto de apoio
(SETel_08_09), Instituto Superior Técnico
[18]
J. F. Alves da Silva, Electrónica Industrial, F. Calouste Gulbenkian, 1998
64
Anexo A
Figura A.1 - Diagrama de blocos do funcionamento do rectificador elevador de duplo estágio de
conversão.
Figura A.2 - Diagrama de blocos do rectificador elevador de duplo estágio de conversão.
65
Figura A.3 - Diagrama de blocos do controlador de tensão do conversor CC-CC do tipo elevador.
Figura A.4 - Diagrama de blocos do controlador de corrente do conversor CC-CC do tipo elevador.
Figura A.5 - Diagrama de blocos do sinal de comando do conversor CC-CC do tipo elevador.
66
Anexo B
Figura B.1 - Diagrama de blocos do funcionamento do rectificador elevador de um único estágio de
conversão.
Figura B.2 - Diagrama de blocos do rectificador elevador de um único estágio de conversão.
67
Figura B.3 - Diagrama de blocos do controlador de tensão do rectificador elevador de um único estágio
de conversão.
Figura B.4 - Diagrama de blocos do controlador de corrente do rectificador elevador de um único estágio
de conversão.
Figura B.5 - Diagrama de blocos do sinal de comando do rectificador elevador de um único estágio de
conversão.
68