www.cursoagoraeupasso.com.br Raciocínio Lógico – CESPE 37

www.cursoagoraeupasso.com.br
DIAGRAMAS LÓGICOS
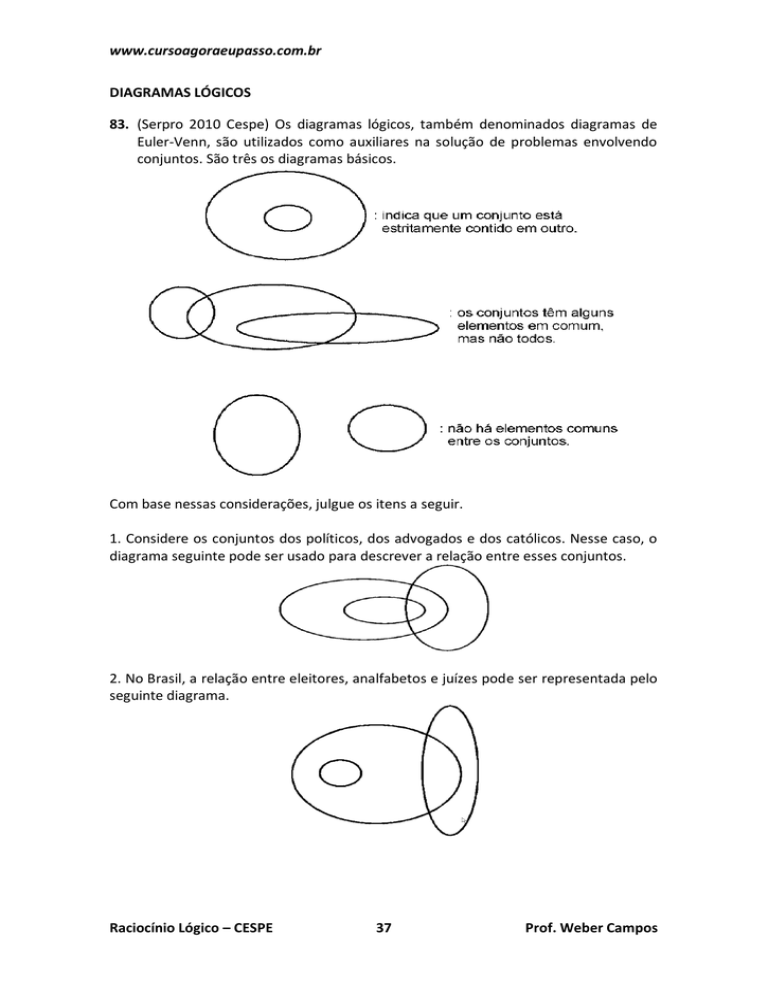
83. (Serpro 2010 Cespe) Os diagramas lógicos, também denominados diagramas de
Euler-Venn, são utilizados como auxiliares na solução de problemas envolvendo
conjuntos. São três os diagramas básicos.
Com base nessas considerações, julgue os itens a seguir.
1. Considere os conjuntos dos políticos, dos advogados e dos católicos. Nesse caso, o
diagrama seguinte pode ser usado para descrever a relação entre esses conjuntos.
2. No Brasil, a relação entre eleitores, analfabetos e juízes pode ser representada pelo
seguinte diagrama.
Raciocínio Lógico – CESPE
37
Prof. Weber Campos
www.cursoagoraeupasso.com.br
3. Considerando os conjuntos dos bacharéis, dos médicos e dos professores
universitários, o diagrama que melhor representa a relação entre esses conjuntos é o
ilustrado a seguir.
84. (SEFAZ/RJ 2011 FGV) Qual dos diagramas abaixo representa melhor a relação
entre mulheres, mães e profissionais de contabilidade?
85. (TRT-9ªRg-2004-FCC) Denota-se respectivamente por A e B os conjuntos de todos
atletas da delegação olímpica argentina e brasileira em Atenas, e por M o
conjunto de todos os atletas que irão ganhar medalhas nessas Olimpíadas. O
diagrama mais adequado para representar possibilidades de intersecção entre os
três conjuntos é
a)
d)
b)
e)
c)
Raciocínio Lógico – CESPE
38
Prof. Weber Campos
www.cursoagoraeupasso.com.br
86. (FCC 2010) Admita as frases seguintes como verdadeiras.
I. Existem futebolistas (F) que surfam (S) e alguns desses futebolistas também são
tenistas (T).
II. Alguns tenistas e futebolistas também jogam vôlei (V).
III. Nenhum jogador de vôlei surfa.
A representação que admite a veracidade das frases é:
87. (PETROBRAS 2007 CESPE) Considere as seguintes frases.
I Todos os empregados da PETROBRAS são ricos.
II Os cariocas são alegres.
III Marcelo é empregado da PETROBRAS.
IV Nenhum indivíduo alegre é rico.
Admitindo que as quatro frases acima sejam verdadeiras e considerando suas
implicações, julgue os itens que se seguem.
1. Nenhum indivíduo rico é alegre, mas os cariocas, apesar de não serem ricos, são
alegres.
2. Marcelo não é carioca, mas é um indivíduo rico.
3. Existe pelo menos um empregado da PETROBRAS que é carioca.
4. Alguns cariocas são ricos, são empregados da PETROBRAS e são alegres.
Raciocínio Lógico – CESPE
39
Prof. Weber Campos
www.cursoagoraeupasso.com.br
88. (PETROBRAS 2007 CESPE) Julgue o item seguinte.
1. Admitindo-se que as proposições funcionais Nenhuma mulher é piloto de fórmula 1
e Alguma mulher é presidente sejam ambas V, então é correto concluir que a
proposição funcional Existe presidente que não é piloto de fórmula 1 tem valoração V.
89. (EMBASA 2010 CESPE) Julgue o item seguinte.
1. Considerando que as proposições “As pessoas que, no banho, fecham a torneira ao
se ensaboar são ambientalmente educadas” e “Existem crianças ambientalmente
educadas” sejam V, então a proposição “Existem crianças que, no banho, fecham a
torneira ao se ensaboar” também será V.
90. Admitindo-se verdadeira a frase "Todos os dingos são bambas”, é correto concluir
que
(A) quem não é dingo é bamba.
(B) existem dingos que não são bambas .
(C) alguns bambas não são dingos.
(D) existem mais bambas do que dingos.
(E) a quantidade de bambas pode ser igual a de dingos.
91. Se todos os jaguadartes são momorrengos e todos os momorrengos são cronópios
então pode-se concluir que:
(A) É possível existir um jaguadarte que não seja momorrengo.
(B) É possível existir um momorrengo que não seja jaguadarte.
(C) Todos os momorrengos são jaguadartes.
(D) É possível existir um jaguadarte que não seja cronópio.
(E) Todos os cronópios são jaguadartes.
Raciocínio Lógico – CESPE
40
Prof. Weber Campos
www.cursoagoraeupasso.com.br
LÓGICA DE ARGUMENTAÇÃO
92. Classifique os argumentos a seguir em válido ou inválido:
a) p1: Todas as crianças gostam de chocolate.
p2: Patrícia é criança.
c: Portanto, Patrícia gosta de chocolate.
b) p1: Todas as crianças gostam de chocolate.
p2: Patrícia não é criança.
c: Portanto, Patrícia não gosta de chocolate.
c) (usar o 2º método)
pq
~p___
q
d) (usar o 2º método)
pq
q____
~p
e) (usar o 3º método)
pq
~p___
q
f) (usar o 3º método)
pq
q____
~p
g)
A  (~B  C)
~A  B
D  ~C_
B  ~D
h)
A  (B  C)
B  ~A
D  ~C____
A  ~D
i)
PQ
Q  R_
PR
Raciocínio Lógico – CESPE
41
Prof. Weber Campos
www.cursoagoraeupasso.com.br
93. (TCE-ES/2004/CESPE) Julgue os itens a seguir:
1. A seguinte argumentação é inválida.
Premissa 1: Todo funcionário que sabe lidar com orçamento conhece contabilidade.
Premissa 2: João é funcionário e não conhece contabilidade.
Conclusão: João não sabe lidar com orçamento.
2. A seguinte argumentação é válida.
Premissa 1: Toda pessoa honesta paga os impostos devidos.
Premissa 2: Carlos paga os impostos devidos.
Conclusão: Carlos é uma pessoa honesta.
94. (Auditor Fiscal de Vitória-ES 2007 CESPE)
A Justiça é perfeita.
A lei foi feita pelo homem.
Toda obra humana é imperfeita.
Logo, a lei é injusta.
Com base nas assertivas que fazem parte do argumento apresentado acima, julgue os
itens subseqüentes.
1. A “lei foi feita pelo homem” é uma premissa desse argumento.
2. A “lei é injusta” é a conclusão desse argumento.
3. Trata-se de exemplo de argumento válido.
95. (PC/ES 2010 CESPE) Um argumento constituído por uma sequência de três
proposições — P1, P2 e P3, em que P1 e P2 são as premissas e P3 é a conclusão —
é considerado válido se, a partir das premissas P1 e P2, assumidas como
verdadeiras, obtém-se a conclusão P3, também verdadeira por consequência
lógica das premissas. A respeito das formas válidas de argumentos, julgue os
próximos itens.
1. Considere a seguinte sequência de proposições:
P1 – Existem policiais que são médicos.
P2 – Nenhum policial é infalível.
P3 – Nenhum médico é infalível.
Nessas condições, é correto concluir que o argumento de premissas P1 e P2 e
conclusão P3 é válido.
2. Se as premissas P1 e P2 de um argumento forem dadas, respectivamente, por
“Todos os leões são pardos” e “Existem gatos que são pardos”, e a sua conclusão P3
for dada por “Existem gatos que são leões”, então essa sequência de proposições
constituirá um argumento válido.
Raciocínio Lógico – CESPE
42
Prof. Weber Campos
www.cursoagoraeupasso.com.br
96. (Agente da Polícia Federal/2004/CESPE) Uma noção básica da lógica é a de que um
argumento é composto de um conjunto de sentenças denominadas premissas e
de uma sentença denominada conclusão. Um argumento é válido se a conclusão é
necessariamente verdadeira sempre que as premissas forem verdadeiras. Com
base nessas informações, julgue os itens que se seguem.
1. Toda premissa de um argumento válido é verdadeira.
2. Se a conclusão é falsa, o argumento não é válido.
3. Se a conclusão é verdadeira, o argumento é válido.
4. É válido o seguinte argumento: todo cachorro é verde, e tudo que é verde é vegetal,
logo todo cachorro é vegetal.
97. (EMBASA 2010 CESPE) Um argumento lógico é uma relação que associa uma
sequência finita de k proposições Pi, 1 ≤ i ≤ k, denominadas premissas, a uma
proposição Q, denominada conclusão. Um argumento lógico será denominado
válido se a veracidade das premissas garantir a veracidade da conclusão.
A partir dessas informações, considere as proposições listadas a seguir.
P1: A atmosfera terrestre impede que parte da radiação solar refletida pela superfície
terrestre seja irradiada para o espaço.
P2: Esse fenômeno é chamado de efeito estufa.
P3: Os gases na atmosfera responsáveis pelo efeito estufa, como o vapor de água e o
CO2, são chamados de gases do efeito estufa.
P4: A emissão de alguns gases do efeito estufa pelas indústrias, pelas queimadas e pelo
tráfego de veículos produzirá aumento no efeito estufa.
Q: A vida na Terra sofrerá grandes mudanças nos próximos 50 anos.
Com base nas definições e nas proposições enunciadas acima, julgue os itens que se
seguem.
1. O argumento lógico em que P1, P2, P3 e P4 são as premissas e Q é a conclusão pode
ser corretamente representado pela expressão [P1  P2  P3  P4]  Q.
2. O argumento lógico em que P1, P2, P3 e P4 são as premissas e Q é a conclusão é um
argumento lógico válido.
98. (SERPRO/2004/ CESPE) Julgue o item a seguir.
1. A argumentação
 Se lógica é fácil, então Sócrates foi mico de circo.
 Lógica não é fácil.
 Sócrates não foi mico de circo.
é válida e tem a forma
 PQ
 ¬P
 ¬Q
Raciocínio Lógico – CESPE
43
Prof. Weber Campos
www.cursoagoraeupasso.com.br
99. (MRE 2008 CESPE) Julgue o item a seguir.
1. Considere como premissas as seguintes proposições:
— “Ou o candidato é brasileiro nato ou o candidato não pode se inscrever no concurso
para ingresso na carreira diplomática.”
— “O candidato não pode inscrever-se no concurso para ingresso na carreira
diplomática.”
Nesse caso, obtém-se uma argumentação lógica válida se for apresentada como
conclusão a proposição: “O candidato não é brasileiro nato.”
100. (TRT 1ª Região Téc Jud 2008 CESPE) Considere que as proposições a seguir têm
valores lógicos V.
- Catarina é ocupante de cargo em comissão CJ.3 ou CJ.4.
- Catarina não é ocupante de cargo em comissão CJ.4 ou Catarina é juíza.
- Catarina não é juíza.
Assinale a opção correspondente à proposição que, como consequência da veracidade
das proposições acima, tem valoração V.
A) Catarina é juíza ou Catarina ocupa cargo em comissão CJ.4.
B) Catarina não ocupa cargo em comissão CJ.3 nem CJ.4.
C) Catarina ocupa cargo em comissão CJ.3.
D) Catarina não ocupa cargo em comissão CJ.4 e Catarina é juíza.
E) Catarina não é juíza, mas ocupa cargo em comissão CJ.4.
101. (SAD PE 2010 CESPE) Um argumento válido é uma sequência finita de
proposições em que algumas são chamadas premissas e assumidas como
verdadeiras, e as demais são conclusões que se garantem verdadeiras em
consequência da veracidade das premissas e de conclusões previamente
estabelecidas.
Suponha que a proposição “Se Josué foi aprovado no concurso e mudou de cidade,
então Josué mudou de emprego” seja uma premissa de um argumento. Se a
proposição “Josué não mudou de emprego” for outra premissa desse argumento, uma
conclusão que garante sua validade é expressa pela proposição
A. Josué foi aprovado no concurso e não mudou de cidade.
B. Josué não foi aprovado no concurso e mudou de cidade.
C. Josué não foi aprovado no concurso ou não mudou de cidade.
D. Se Josué não mudou de emprego, então Josué não mudou de cidade.
E. Se Josué não mudou de emprego, então Josué não foi aprovado no concurso.
102. (SEGER/ES 2011 CESPE)
— Começo de mês é tempo de receber salário.
— Se as contas chegam, o dinheiro (salário) sai.
— Se o dinheiro (salário) sai, a conta fica no vermelho muito rapidamente.
— Se a conta fica no vermelho muito rapidamente, então a alegria dura pouco.
— As contas chegam.
Pressupondo que as premissas apresentadas acima sejam verdadeiras e considerando
as propriedades gerais dos argumentos, julgue os itens subsequentes.
Raciocínio Lógico – CESPE
44
Prof. Weber Campos
www.cursoagoraeupasso.com.br
1. A afirmação “Começo do mês é tempo de receber salário, porém a alegria dura
pouco” é uma conclusão válida a partir das premissas apresentadas acima.
2. A afirmação “Se as contas chegam, então a alegria dura pouco” é uma conclusão
válida a partir das premissas apresentadas acima.
103. (Escrivão da PF 2009 Cespe)
1. A sequência de proposições a seguir constitui uma dedução correta.
Se Carlos não estudou, então ele fracassou na prova de Física.
Se Carlos jogou futebol, então ele não estudou.
Carlos não fracassou na prova de Física.
Carlos não jogou futebol.
2. Considere que as proposições da sequência a seguir sejam verdadeiras.
Se Fred é policial, então ele tem porte de arma.
Fred mora em São Paulo ou ele é engenheiro.
Se Fred é engenheiro, então ele faz cálculos estruturais.
Fred não tem porte de arma.
Se Fred mora em São Paulo, então ele é policial.
Nesse caso, é correto inferir que a proposição “Fred não mora em São Paulo” é uma
conclusão verdadeira com base nessa sequência.
104. (MRE 2008 CESPE) Julgue os itens a seguir.
1. Considere que as premissas de um argumento incluem a proposição: “O barão do
Rio Branco foi professor e San Tiago Dantas foi advogado”. Nesse caso, a proposição
“Se San Tiago Dantas não foi advogado, então o barão do Rio Branco foi professor” é
uma conclusão que torna o argumento correto.
105. (Policia Civil - ES 2009 CESPE) Julgue os itens a seguir, acerca de raciocínio lógico.
1. Considere que o delegado faça a seguinte afirmação para o acusado: “O senhor
espanca a sua esposa, pois foi acusado de maltratá-la’’. Nesse caso, é correto afirmar
que o argumento formulado pelo delegado constitui uma falácia.
106. (MPE Tocantins – Analista – 2006 CESPE) Uma argumentação é uma seqüência
finita de k proposições (que podem estar enumeradas) em que as (k -1) primeiras
proposições ou são premissas (hipóteses) ou são colocadas na argumentação por
alguma regra de dedução. A k-ésima proposição é a conclusão da argumentação.
Sendo P, Q e R proposições, considere como regras de dedução as seguintes: se P e P
 Q estão presentes em uma argumentação, então Q pode ser colocada na
argumentação; se P  Q e Q  R estão presentes em uma argumentação, então P 
R pode ser colocada na argumentação; se PQ está presente em uma argumentação,
então tanto P quanto Q podem ser colocadas na argumentação.
Duas proposições são equivalentes quando tiverem as mesmas avaliações V ou
F. Portanto, sempre podem ser colocadas em uma argumentação como uma forma de
“reescrever” alguma proposição já presente na argumentação. São equivalentes, por
exemplo, as proposições A  B, ¬B¬A e ¬AB. Uma argumentação é válida sempre
Raciocínio Lógico – CESPE
45
Prof. Weber Campos
www.cursoagoraeupasso.com.br
que, a partir das premissas que são avaliadas como V, obtém-se (pelo uso das regras
de dedução ou por equivalência) uma conclusão que é também avaliada como V.
Com base nas informações do texto I, julgue os itens que se seguem.
1. É correto afirmar que, simbolizada adequadamente, a argumentação abaixo é
válida.
1. Se um casal é feliz, então os parceiros têm objetivos comuns.
2. Se os parceiros têm objetivos comuns, então trabalham no mesmo Ministério
Público.
3. Há rompimento se o casal é infeliz.
4. Há rompimento se os parceiros não trabalham no mesmo Ministério Público.
2. A seqüência de proposições abaixo não é uma argumentação válida.
1. Se Filomena levou a escultura ou Silva mentiu, então um crime foi cometido.
2. Silva não estava em casa.
3. Se um crime foi cometido, então Silva estava em casa.
4. Filomena não levou a escultura.
3. Considere o seguinte texto: “Se há mais pares de sapatos do que caixas para
acomodá-los, então dois pares de sapatos são colocados em uma mesma caixa. Dois
pares de sapatos são colocados em uma mesma caixa. Conclui-se então que há mais
pares de sapatos do que caixas para acomodá-los”.
Nesse caso, o texto expressa uma argumentação que não é válida.
4. Considere uma argumentação em que as duas proposições simbólicas abaixo são
premissas, isto é, têm avaliação V.
1. (A¬B)  C
2. ¬C
Neste caso, se a conclusão for a proposição (¬AB), tem-se uma argumentação
válida.
5. Considere que as proposições “Todo advogado sabe lógica” e “Todo funcionário do
fórum é advogado” são premissas de uma argumentação cuja conclusão é “Todo
funcionário do fórum sabe lógica”. Então essa argumentação é válida.
6. Considere uma argumentação em que duas premissas são da forma
1. Nenhum A é B.
2. Todo C é A.
e a conclusão é da forma “Nenhum C é B”. Essa argumentação não pode ser
considerada válida.
7. Considere que em uma argumentação uma premissa seja “Se um número x é
divisível por 6 então x é divisível por 3”. Se a conclusão da argumentação for “Se um
número x é divisível por 6, então a soma de seus algarismos é divisível por 3”, é
correto afirmar que a proposição “Se x é divisível por 3, então a soma de seus
algarismos é divisível por 3” tem de ser outra premissa dessa argumentação.
Raciocínio Lógico – CESPE
46
Prof. Weber Campos
www.cursoagoraeupasso.com.br
107. (TRE/ES 2010 Cespe) Argumento é a afirmação de que uma sequência de
proposições, denominadas premissas, acarreta outra proposição, denominada
conclusão. Um argumento é válido quando a conclusão é verdadeira sempre que
as premissas são todas verdadeiras.
1. A partir das premissas “Se Joelson irá a uma festa e procurará uma namorada, então
Joelson precisa cortar o cabelo”, “Se Joelson é casado, então, não precisa cortar o
cabelo” e “Se Joelson é casado, então, não procurará uma namorada”, pode-se
concluir corretamente que Joelson não é casado.
2. O argumento cujas premissas são “Quem é casado não precisa cortar o cabelo” e
“Quem vai procurar uma namorada precisa cortar o cabelo” e cuja conclusão é “Quem
é casado não vai procurar uma namorada” é válido.
108. (Assembléia Legislativa do Ceará 2011 CESPE) A fim de convencer um cliente a
contratar os serviços de cartão pré-pago, o gerente de uma instituição financeira
argumentou com as seguintes proposições:
P1: Se uma pessoa não possui conta-corrente nem cartão pré-pago, então ela efetua
seus pagamentos em dinheiro.
P2: Se uma pessoa efetua seus pagamentos em dinheiro, então ela carrega muito
dinheiro no bolso.
P3: Se uma pessoa carrega muito dinheiro no bolso, então ela corre o risco de ser
assaltada.
Com base na situação apresentada acima, julgue os itens subsequentes.
1. O argumento composto pelas premissas P1, P2 e P3 e pela conclusão “Se uma
pessoa possui conta-corrente ou cartão pré-pago, então ela não corre o risco de ser
assaltada” é um argumento válido.
109. (DETRAN/ES 2010 CESPE) No ambiente de trabalho, é comum se ouvir o seguinte
dito popular:
“Quem trabalha pouco erra pouco. Quem não trabalha não erra. Quem não erra é
promovido. Logo, quem não trabalha é promovido.”
Com relação ao argumento desse dito popular, julgue os itens que se seguem.
1. Do ponto de vista lógico, o argumento apresentado no dito popular é válido.
2. Admitindo-se que a negação da sentença “aquela pessoa trabalha pouco” possa ser
expressa por “aquela pessoa trabalha muito”, das premissas do argumento do referido
dito popular é correto concluir que “quem trabalha muito erra muito”.
110. (SEBRAE 2010 CESPE) Ainda tendo como referência as informações do texto,
julgue os próximos itens.
1. Considere a sequência de proposições a seguir.
A1: O concurso destina-se a selecionar candidatos a cargos dos níveis fundamental,
médio e superior.
A2: 2.700 candidatos se inscreveram para o concurso.
A3: Nenhum candidato se inscreveu a cargos de níveis diferentes.
Raciocínio Lógico – CESPE
47
Prof. Weber Campos
www.cursoagoraeupasso.com.br
A4: A quantidade de inscritos para os cargos de nível médio foi o dobro da quantidade
de inscritos para os cargos de nível superior.
A5: A quantidade de inscritos para os cargos de nível fundamental foi o triplo da
quantidade de inscritos para os cargos de nível médio.
B: Apenas 300 candidatos se inscreveram para os cargos de nível superior.
Nesse caso, se as proposições de A1 a A5 forem premissas verdadeiras de um
argumento e se B for a conclusão, então elas constituirão um argumento válido.
111. (Agente da PF 2004 Cespe) Quando Paulo estuda, ele é aprovado nos concursos
em que se inscreve. Como ele não estudou recentemente, não deve ser
aprovado neste concurso.
Em cada um dos itens a seguir, julgue se o argumento apresentado tem estrutura
lógica equivalente à do texto acima.
1. Sempre que Paulo insulta Maria, ela fica aborrecida. Como Paulo não insultou Maria
recentemente, ela não deve estar aborrecida.
2. Quando Paulo gosta de alguém, ele não mede esforços para oferecer ajuda. Como
Maria gosta muito de Paulo, ele vai ajudá-la a responder as questões de direito
constitucional.
3. Quando os críticos literários recomendam a leitura de um livro, muitas pessoas
compram o livro e o lêem. O livro sobre viagens maravilhosas, lançado recentemente,
não recebeu comentários favoráveis dos críticos literários, assim, não deve ser lido por
muitas pessoas.
4. Toda vez que Paulo chega a casa, seu cachorro late e corre a seu encontro. Hoje
Paulo viajou, logo seu cachorro está triste.
Raciocínio Lógico – CESPE
48
Prof. Weber Campos
www.cursoagoraeupasso.com.br
LÓGICA DE PRIMEIRA ORDEM
112. Julgue as proposições seguintes quanto ao seu valor lógico (verdadeiro ou falso):
a) (x  R)( x  4  4)
b) (x  R)( x  4  4)
c) (x  )( x  4  4)
d) (x  R)( x  x)
e) (x  )(2 x  4  x  3)
f)
(x  )(2 x  4  x  3)
g) (x  )( x 2  2 x  15)
h) (x  Z)((x2 ≤ 0) ou (x+2>x+3))
i) (x  Z)((x > 0)  (x + 2) é par)
113. Considere o conjunto A = {1, 2, 3, 4, 5}. Determine o valor lógico das proposições
a seguir:
a) (x  A) (x+4=7)
b) (y  A) (y+3<5)
c) (y  A) (y+2<7)
d) (z  A) (4z – z2  0)
114. Determine a negação das seguintes proposições:
a) x  R, x≥0 ou x2 + 1<0.
b) n  Z, se n é divisível por 2, então n é par.
115. (MPE Tocantins – Técnico – 2006 CESPE) Uma proposição pode ser expressa em
função de uma ou mais variáveis. Por exemplo, afirmativas tais como “para cada
x, P(x)” ou “existe x, P(x)” são proposições que podem ser interpretadas como V
ou F, de acordo com o conjunto de valores assumidos pela variável x e da
interpretação dada ao predicado P.
A negação da proposição “para cada x, P(x)” é “existe x, ¬P(x)”. A negação da
proposição “existe x, P(x)” é “para cada x, ¬P(x)”.
Raciocínio Lógico – CESPE
49
Prof. Weber Campos
www.cursoagoraeupasso.com.br
Considerando as informações apresentadas acima, julgue os itens subseqüentes.
1. A proposição “para cada x, (x + 2) > 7” é interpretada como V para x pertencente ao
conjunto {6, 7, 8, 9}. C
2. Se x pertence ao conjunto {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, então a proposição “existe x, (x
+ 6) < 4” é V.
3. A negação das proposições “para cada x, (x + 4)  10” e “existe x, (x + 3) < 8” é
verdadeira para x pertencente ao conjunto {2, 4, 6, 8, 10}.
116. (PM Ceará 2008 CESPE) Julgue os seguintes itens.
1. Se Q é o conjunto dos números racionais, então a proposição (x)(xQ)(x2+x-1 = 0) é
julgada como V.
2. Se N é o conjunto dos números inteiros, então a proposição (x)(xN)[(x-1)x(x+1) é
divisível por 3] é julgada como V.
117. (TRT 5ª região 2008 CESPE) Julgue os seguintes itens.
1. Se Q é o conjunto dos números racionais, então a proposição (x)(xQ e x > 0)(x2 >
x) é valorada como F.
2. Se Q é o conjunto dos números racionais, então a proposição (x)(xQ)(x2 = 2) é
valorada como V.
118. (INSS Analista 2008 CESPE) Algumas sentenças são chamadas abertas porque são
passíveis de interpretação para que possam ser julgadas como verdadeiras (V) ou
falsas (F). Se a sentença aberta for uma expressão da forma xP(x), lida como
“para todo x, P(x)”, em que x é um elemento qualquer de um conjunto U, e P(x) é
uma propriedade a respeito dos elementos de U, então é preciso explicitar U e P
para que seja possível fazer o julgamento como V ou como F.
A partir das definições acima, julgue os itens a seguir.
1. Se U for o conjunto de todos os funcionários públicos e P(x) for a propriedade “x é
funcionário do INSS”, então é falsa a sentença xP(x).
2. Considere-se que U seja o conjunto dos funcionários do INSS, P(x) seja a propriedade
“x é funcionário do INSS” e Q(x) seja a propriedade “x tem mais de 35 anos de
idade”. Desse modo, é correto afirmar que duas das formas apresentadas na
lista abaixo simbolizam a proposição Todos os funcionários do INSS têm mais de
35 anos de idade.
(i) x(se Q(x) então P(x))
(ii) x(P(x) ou Q(x))
(iii) x(se P(x) então Q(x))
Raciocínio Lógico – CESPE
50
Prof. Weber Campos
www.cursoagoraeupasso.com.br
119. (PETROBRAS 2007 CESPE) Uma proposição funcional simbólica é uma expressão
que contém variáveis x, y, z, ... e predicados P, Q, R, ..., que dizem respeito às
variáveis, e pode ou não conter os símbolos quantificadores denotados por 
(para todo) e  (existe) que atuam sobre as variáveis. Uma proposição funcional
pode ser julgada como verdadeira (V) ou falsa (F), dependendo do conjunto de
valores que são atribuídos às variáveis e à interpretação dada aos predicados.
Proposições funcionais são expressões, por exemplo, do tipo (x)P(x), (y)Q(y),
(x)(y)P(x, y) etc.
A partir das informações acima, julgue o item a seguir.
1. Se as variáveis x e y pertencem ao conjunto A = {2, 3, 4} e o predicado P(x, y) é
interpretado como x2y+2, então a proposição funcional (x)(y)P(x, y) é avaliada
como verdadeira.
120. (Papiloscopista 2004 CESPE) Considere as quatro sentenças enumeradas a seguir.
I
II
III
IV
Para cada y, existe algum x, tal que x < y.
Para cada x e para cada y, se x < y então existe algum z, tal que x < z e z < y.
Para cada x, se 0 < x, então existe algum y tal que x = y × y.
Existe algum x tal que, para cada y, x < y.
Suponha que, nessas sentenças, x, y e z sejam variáveis que podem assumir
valores no conjunto dos números naturais (N), no dos números inteiros (Z), no dos
números racionais (Q) ou no conjunto dos números reais (R).
Em cada linha da tabela a seguir, são atribuídas valorações V e F, para cada uma
das quatro sentenças enumeradas acima, de acordo com o conjunto no qual as
variáveis x, y e z assumem valores.
Julgue os itens subseqüentes, a respeito dessas sentenças.
1. As avaliações dadas para as sentenças I e III estão corretas.
2. As avaliações dadas para as sentenças II e IV estão corretas.
Raciocínio Lógico – CESPE
51
Prof. Weber Campos
www.cursoagoraeupasso.com.br
GABARITO
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
E C Anulada
a
e
a
C C E E
C
E
e
b
Vál. Inv. Vál. Inv. Vál. Inv. Inv. Vál. Inv.
E E
C C C
E E
E E E C
E E
E
E
c
c
C C
C C
C
C
C E C C C E C
E C
E
C E
C
C E E E
C E C E E C C C E
C C E E
x  R, x<0 e x2 + 1≥0
n  Z, n é divisível por 2 e n não é par
C E E
E C
C E
C E
C
E C
Raciocínio Lógico – CESPE
52
Prof. Weber Campos