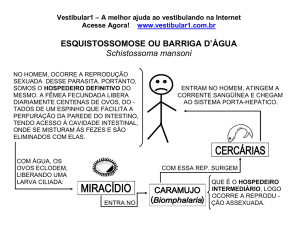
Respostas de MAIO Dia 1: O menor número de ovos é 91. Dia 2: O

Respostas de MAIO
Dia 1: O menor número de ovos é 91.
Dia 2: O nível da água baixa. No barquinho, a moeda desloca a mesma massa de
água que a do barquinho, portanto, um volume maior que o da moeda. Na água, a
moeda desloca apenas em volume igual ao seu.
Dia 3: 6 X 6 – 6
Dia 4:
Dia 5: Escorregue o palito da parte inferior da taça para a esquerda. Depois, mova
o palito que está do lado “direito” da taça para a esquerda da haste da taça. Ela
estará de ponta cabeça e a azeitona ficará de fora.
Dia 6: 6
11 18
27
A sequência é formada elevando-se ao quadrado os números 2,3,4... e somandolhes 2 em cada caso.
Dia 7: Basta mudar de posição os quadrados rosa, vermelho e azul claro.
Dia 8: Homens 18, mulheres 22 e crianças 40
Dia 9: 30.32.34.
Dia 10: 42.
Dia 11: O número procurado é 86421.
Dia 12: Temos um sistema envolvendo quatro variáveis (esfirra, saco de
salgadinhos, refrigerante e maço de cigarros). Porém, temos apenas duas
equações:
a+b+c+d = 7,11
a.b.c.d= 7,11
Para resolver o problema, o jeito é determinar o preço de dois itens, e depois
calcular os outros dois. Por exemplo, vamos determinar que a esfirra custa R$1,50
e o saco de salgadinhos custa R$1,25. Então teríamos um sistema fácil de resolver:
1,50+1,25+c+d = 7,11
1,50.1,25.c.d = 7,11
Isolando o c na primeira equação temos:
c = 7,11-1,50-1,25-d
c = 4,36 – d
Substituindo na segunda equação temos:
1,50.1,25.(4,36-d).d = 7,11
-1,875d2 + 8,175d – 7,11 = 0
d=1,20 ou d=3,16
Usando d=1,20, achamos o valor de c:
c = 4,36-1,20 = 3,16
Portanto, um conjunto de valores possíveis para os itens são:
Esfirra: R$1,50
Salgadinhos: R$1,25
Refrigerante: R$3,16
Cigarros: R$1,20
Dia 13: Adroaldson tinha um nota de R$ 50,00, uma de R$ 5,00 e quatro de R$
2,00.
Dia 14: Os algarismos estarão todos alterados, pela primeira vez, quando o relógio
marcar 20:00:00, ou seja, quando se passarem 147 segundos.
Dia 15:
Sabemos que, excetuando-se o número 2, todos os primos são ímpares.
Sabemos também que a soma de dois números ímpares dá sempre um
número par
E como a soma de dois números primos esta dando um número ímpar,
concluimos, que um desses primos é o dois e, com isso,
descobrimos que o outro primo será 33 - 2 = 31
=2
Dessa maneira, nossa primeira soma
= 3.
a + c = 33
a = 31 e c
a + b = 34, para a = 3, nos dará b
E dessa forma, teremos : a = 31 ; b = 3 e c = 2
36
a + b + c = 31 + 3 + 2 =
Dia 16: Um tem 8 anos e o outro tem 32.
Dia 17: PA de razão 4
Dia 18: Bem interessante a sua questão, porém devemos esclarecer o significado
da união de todas essas letras , ok :
x x x x ---> 1000x + 100x + 10x + x = 1111 x
y y y y ---> 1111 y
z z z z ---> 1111 z
y x x x z ---> 10000 y + 1000 x + 100 x + 10 x + z
Logo , teremos :
1111 x + 1111 y + 1111 z = 10000 y + 1110 x + z
1111 x - 1110 x + 1111 y - 10000 y + 1111 z - z = 0
x - 8889 y + 1110 z = 0 ---> y = (1110 z + x )/ 8889
Como y deve representar um número natural com apenas 1 algarismo , então o
numerador da fração acima (1110 z + x ) deve ser múltiplo de 8889 !!!
Como 0 <= z <= 9 , então 1110 z + x = 8889 --> y = 8889/8889 --> y = 1
1110 z + x = 8880 + 9 = 1110 . 8 + 9 ----> z = 8 , x = 9
Portanto , x = 9 , y = 1 , z = 8
**************************************...
Verificação dos resultados obtidos ( x = 9 , y = 1 , z = 8 )
9999 + 1111 + 8888 = 19998
19998 = 19998 --> sentença verdadeira
Dia 19: Suponhamos que estamos procurando o número X. Observe essas
condições exigidas pelo problema:
X dividido por 2 dá resto 1.
X dividido por 3 dá resto 2.
e assim por diante até:
X dividido por 6 dá resto 5.
Então podemos notar que o resto dá sempre uma unidade a menos do que o
divisor.
Isso significa que o número seguinte ao número X, ou seja, X+1, será divisível
por 2, 3, 4, 5 e 6.
Já que X+1 é divisível por esses cinco números, então o número X+1 pode ser
igual a 4x5x6=120.
Portanto, se X+1 é igual a 120, o número X que estamos procurando é 119,
que também é divisível por 7.
Dia 20: ( 6 x 5 -7)1
Dia 21: Comecemos do fim para o início.
Se lhe sobraram 10 ovos é porque o último freguês levou um total de 11 ovos. Com
isso, na última venda ele tinha
11 + 10 = 21 ovos ???
Expliquemos:
Se não foi quebrado nenhum ovo, os resultados sempre serão números naturais. Se
a metade mais meio ovo dá um número natural, a metade era um número
"quebrado".
E esse acréscimo de meio ovo vem, justamente da metade do vendedor. Se ele
ficou com 10 ovos, ele tinha 10,5 ovos, que é a metade 10,5 x 2 = 21.
Como ele dá esse meio ovo para o comprador ele fica com 10 ovos (10,5 - 0,5) e o
comprador com 11 ovos (10,5 + 0,5)
Após a segunda compra ele tinha 21 ovos e o comprador, pelo exposto acima, teria
22 ovos.
Com isso, após a primeira compra os ovos eram 21 + 22 = 43 ovos
Se após a primeira compra ele tinha 43 ovos e o comprador, pelo já exposto , teria
44 ovos.
Com isso, originalmente, os ovos eram 43 + 44 = 87 ovos.
Será que estamos certos?
1° Comprador: Se eram 87 ovos, a metade do comprador seria 87 :2 = 43,5 e a
metade do vendedor seria, também, 43,5 ovos.
Para não quebrar nenhum ovo o vendedor dá seu meio ovo para o comprador.
O vendedor fica com: 43,5 - 0,5 = 43 ovos e o comprador com : 43,5 + 0,5 = 44
ovos.
2° Comprador: Se eram 43 ovos, a metade do comprador seria 43 :2 = 21,5 e a
metade do vendedor seria, também, 21,5 ovos.
Para não quebrar nenhum ovo o vendedor dá seu meio ovo para o comprador.
O vendedor fica com: 21,5 - 0,5 = 21 ovos e o comprador com : 21,5 + 0,5 = 22
ovos.
3° Comprador: Se eram 21 ovos, a metade do comprador seria 21 :2 = 10,5 e a
metade do vendedor seria, também, 10,5 ovos.
Para não quebrar nenhum ovo o vendedor dá seu meio ovo para o comprador.
O vendedor fica com: 10,5 - 0,5 = 10 ovos e o comprador com : 10,5 + 0,5 = 11
ovos.
Foram comprados 44 + 22 + 11 = 77 ovos e mais os 10 restantes = 87 ovos.
Dia 22: DAVI
Dia 23: 96 pessoas
Dia 24:1111!
Dia 25: 666+66+66+66+66+66+ +
+ +
Dia 26: Descoberto
Dia 27: Demorará 60 s
Dia 28: O número 6
Dia 29:qualquer numero entre 0 e 1. Como raiz de 1/4= 1/2
Dia 30:
Dia 31:
X + (x+3) + (x+ 6) =63
X+ x+x = 63 -3 -6
3x = 54
X=18
Os números são 18, 21 e 24.