##### QUESTÕES RESOLVIDAS DE GEOMETRIA II - MORGADO = CELSO BRASIL

Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
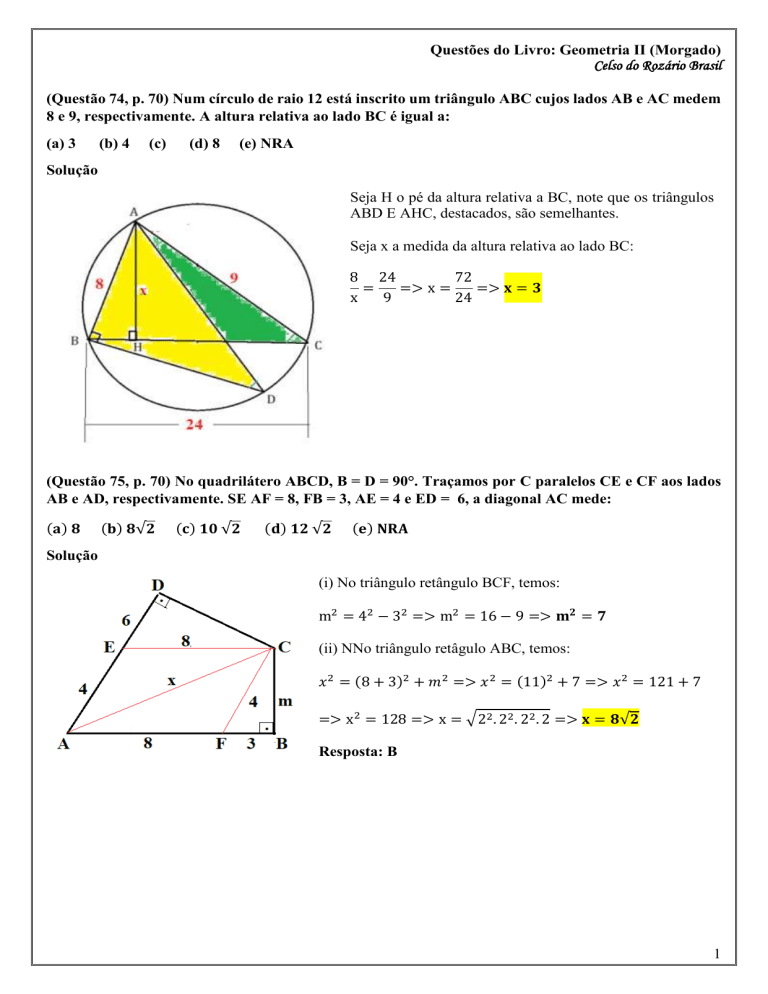
(Questão 74, p. 70) Num círculo de raio 12 está inscrito um triângulo ABC cujos lados AB e AC medem
8 e 9, respectivamente. A altura relativa ao lado BC é igual a:
(a) 3
(b) 4
(c)
(d) 8
(e) NRA
Solução
Seja H o pé da altura relativa a BC, note que os triângulos
ABD E AHC, destacados, são semelhantes.
Seja x a medida da altura relativa ao lado BC:
8 24
72
=
=> x =
=> 𝐱 = 𝟑
x
9
24
(Questão 75, p. 70) No quadrilátero ABCD, B = D = 90°. Traçamos por C paralelos CE e CF aos lados
AB e AD, respectivamente. SE AF = 8, FB = 3, AE = 4 e ED = 6, a diagonal AC mede:
(𝐚) 𝟖
(𝐛) 𝟖√𝟐
(𝐜) 𝟏𝟎 √𝟐
(𝐝) 𝟏𝟐 √𝟐
(𝐞) 𝐍𝐑𝐀
Solução
(i) No triângulo retângulo BCF, temos:
m2 = 42 − 32 => m2 = 16 − 9 => 𝐦𝟐 = 𝟕
(ii) NNo triângulo retâgulo ABC, temos:
𝑥 2 = (8 + 3)2 + 𝑚2 => 𝑥 2 = (11)2 + 7 => 𝑥 2 = 121 + 7
=> x 2 = 128 => x = √22 . 22 . 22 . 2 => 𝐱 = 𝟖√𝟐
Resposta: B
1
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(Questão 76, p. 70) Considerando a figura abaixo, a soma dos diâmetros de todos os círculos é:
(a) 15
(b) 12
(c) 8
(d) 6
(e) NRA.
Solução
Sejam:
O, O', O" centros da maior, da média, da menor
2
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
E o vértice do ângulo de 60º
R, r os raios da média e da menor circunferências
(A, B), (A',B'), (A", B") são pontos de tangência da maior, da média e da menor com as retas
(i) Traçando o segmento OE e os raios OA = OB = OM = 4,
(ii) O'A' = O'B' = O'M = O'N = R e
(iii) O"A" = O"B" = O"N
(v) OO’ = 4 + R => O'O" = R + r
(vi) Trançando uma perpendicular a OB, no ponto P -----> PB = O’B’ = R ---> OP = 4 - R
Traçando por O" uma perpendicular a O'B', no ponto Q ---> QB' = O"B" = r ---> O'Q = R - r
(vii) No triângulo retângulo OBE, temos:
Cos 60° =
OB
1
4
=> =
=> 𝑶𝑬 = 𝟖
OE
2 𝑂𝐸
(viii) No triângulo retângulo OPO'
Cos 60° =
OP
1 4−𝑅
1 4−𝑅
=> =
(𝑁𝑜𝑡𝑒 𝑞𝑢𝑒: 𝑂𝑂′ = 4 + 𝑅 (𝑣)). 𝐿𝑜𝑔𝑜: =
=> 8 − 2𝑅 = 4 + 𝑅 =>
′
′
𝑂𝑂
2
𝑂𝑂
2 4+𝑅
−2R − R = 4 − 8 => −3R = −4 => R =
−4
𝟒
=> 𝐑 =
−3
𝟑
(ix) No triângulo retângulo O’QO”, temos:
4
4 − 3𝑟
R−r
1 3−𝑟
1
3 => 4 + 3𝑟 = 2 (4 − 3𝑟 ) => 4 + 3𝑟 = 8 − 6𝑟 =>
Cos 60° =
=> =
=> =
4
𝑂′𝑂"
2 𝑅+𝑟
2
3
3
3+𝑟
𝟒
9𝑟 = 4 => 𝐫 = 𝟗 ?????????????????????????????
(Questão 77, p. 71)
3
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
Solução
No triângulo retângulo ABC, temos:
(12)2 = 𝑥. 18 => 144 = 18𝑥 => 𝑥 =
144
=>
18
𝐱=𝟖
Resposta: B
̅̅̅̅ em D e o círculo
(Questão 79, p. 71) Em um triângulo ABC, a bissetriz interna  encontra 𝑩𝑪
circunscrito em E. Se AB = 8, AC = 6 e DE = 3, calcule o comprimento da bissetriz AD.
(a) 9
(b) 10
(c) 12
(d) 13
(e) NRA
Solução
Observação: O valor correto do segmento AB é 18.
Vamos chamar AD de “x”, logo:
18.6 = x (x + 3) => 108 = x² + 3x => x² + 3x – 108 = 0
∆ = 9 + 432 => ∆ = 𝟒𝟒𝟏
−3 + 21
x′ =
=> 𝒙′ = 𝟗
−3 ± 21
2
𝒙=
=> {
−3 − 21
2
𝒙" =
=> x" = −12
2
Resposta: AD = x = 9 (A)
4
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
Aplicando a relação: h² = m.n, temos:
x 2 = 8.18 => x 2 = 144 => x = 12 ∴ AB = 12 + 12 => 𝐀𝐁 = 𝟐𝟒
𝐶
̂ 𝐸̂
Porque 𝐶̂ + 𝐸̂ = 180°, 2 + 2 = 90°, sendo o triângulo
OCE retângulo em O. Como ̅̅̅̅
𝑂𝐹 é altura relativa à
hipotenusa e como CJ = CF = 6 e EF = EL = x, pela
relação métrica: h² = m.n, temos:
32 = 6. x => 9 = 6x => x =
DE = x + x => DE =
9 3
𝟑
: => 𝐱 =
6 3
𝟐
3 3
6
+ => DE = => 𝐃𝐄 = 𝟑
2 2
2
5
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(Questão 84, p. 80) Em um triângulo ABC, as medianas que partem de A e de B são perpendiculares.
Se BC = 8 e AC = 6, calcule AB.
Solução
(i) No triângulo retângulo amarelo, por Pitágoras,
temos:
(2a)2 + 𝑏 2 = 32 => 𝟒𝒂𝟐 + 𝒃𝟐 = 𝟗 (𝒊)
(ii) No triângulo retângulo verde, por Pitágoras, temos:
(2𝑏)2 + 𝑎2 = 42 => 𝟒𝒃𝟐 + 𝒂𝟐 = 𝟏𝟔 (𝒊𝒊)
(iii) Somando (i) e (ii), temos:
a2 + 𝑏 2 = 5 (4) => 𝟒𝒂𝟐 + 𝟒𝒃𝟐 = 𝟐𝟎 (𝒊𝒊𝒊)
(iv) No triângulo retângulo róseo, temos:
(2𝑎)2 + (2𝑏)2 = (𝐴𝐵)2 => 𝟒𝒂𝟐 + 𝟒𝒃𝟐 = (𝑨𝑩)𝟐 (𝒊𝒗)
(v) Substituindo (iii) em (iv), temos:
4a2 + 4b2 = (AB)2 => 20 = (AB)2 => AB = √20 => 𝐀𝐁 = 𝟐√𝟓
(Questão 195) Sendo equilátero o triângulo da figura, calcule o valor da área assinalada.
6
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
Solução


. O lado do triângulo equilátero ABC vale 6
. O raio r é igual a 1/3 da altura. Logo:
r=
1
L √3
. h → (h =
)
3
2
r=
1 L√3
1 6√3
.(
)→r= (
)→
3
2
3 2
r=
6
√3 →
6
𝐫 = √𝟑
𝐒𝐚𝐬𝐬𝐢𝐧𝐚𝐥𝐚𝐝𝐚 =
Sassinalada
𝐒𝐭𝐫𝐢â𝐧𝐠𝐮𝐥𝐨
− Á𝐫𝐞𝐚 𝐝𝐨 𝐜í𝐫𝐜𝐮𝐥𝐨 →
𝟑
L2 √3
= 4 − πr 2 →
3
Sassinalada =
L2 √3
− πr 2 → mmc = 12
12
Sassinalada =
L2 √3 − 12πr²
12
Sassinalada =
6². √3 − 12π(√3)²
→
12
Sassinalada =
36. √3 − 36π 12
:
→
12
12
𝐒𝐚𝐬𝐬𝐢𝐧𝐚𝐥𝐚𝐝𝐚 = 𝟑√𝟑 − 𝛑
7
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
197. Um triângulo de altura h é dividido por uma reta paralela à base em duas partes equivalentes.
Calcule a distância desta reta ao vértice.
Solução
Pelo enunciado da questão, devemos ter o seguinte:
Note que os triângulos ADE e ABC são semelhantes.
A razão de semelhança (k) entre ambos vale:
k=
x
h
Sabemos que a razão entre as áreas é igual ao quadrado da razão
de semelhança. Logo:
S
x 2 1 x2
h2
h2
h √2
𝐡√𝟐
=( ) → =
→ 2x 2 = h2 → x 2 =
→x=√ →x=
.
→𝐱=
2S
h
2 h²
2
2
𝟐
√2 √2
198. A figura mostra um quadrado e seu círculo circunscrito. Se a área assinalada é igual a 𝝅 − 𝟐,
calcule o lado do quadrado.
8
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
Solução
Sassinalada =
Scírculo
− Área do triângulo AOB
4
π−2 =
πR2 R. R
πR2 R2
−
→π−2=
−
→
4
2
4
2
π−2 =
πR2 − 2R2
→
4
𝐑𝟐 = 𝟒
No triângulo AOB, por Pitágoras, temos:
A = (AB)2 = R2 + R2 → (AB)2 = 4 + 4 → (AB)2 = 8 → 𝐀𝐁 = 𝟐√𝟐
Resposta: O lado do quadrado vale: 𝟐√𝟐
199. Num triângulo isósceles ABC, AB =AC = a. Calcule a sua área sabendo que é máxima.
Solução
(i) No triângulo retângulo ABH, temos:
h
Seno  = → 𝐡 = 𝐚. 𝐬𝐞𝐧𝐨 Â
a
(ii) Área do triângulo ABC:
S=
a. h
a. a. seno Â
a2 . seno Â
→S=
→S=
2
2
2
(iii) A área será máxima se o seno  = 1. Logo:
9
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
a2 . 1
S=
→
2
𝐒=
𝐚𝟐
𝟐
202. Calcule a área do quadrado inscrito em um triângulo de base 12 e altura 6.
Solução
10
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
Note que os triângulos ABC e ADE são
semelhantes. Logo:
6−𝑎
6
6−𝑎 1
=
→
= → 12 − 2𝑎 = 𝑎 →
𝑎
12
𝑎
2
3𝑎 = 12 → 𝑎 = 4
Área do quadrado = a² => 4² => 16
206. Calcule a área do retângulo de perímetro igual a 14, sabendo que a sua diagonal mede 5.
(a) 6
(b) 8
(c) 12
(d) 16
Solução
(i) Perímetro (P):
P = 2a + 2b → 2a + 2b = 14 → 𝐚 + 𝐛 = 𝟕(𝐢)
(ii) No triângulo retângulo cinza, temos:
52 = a2 + b2 → 𝐚𝟐 + 𝐛𝟐 = 𝟐𝟓(ii)
(iii) Isolando o valor de “a” na equação (i) e substituindo na equação (ii), temos:
a + b = 7 → 𝐚 = (𝟕 − 𝐛)
11
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
a2 + b2 = 25 → (7 − b)2 + b2 = 25 → 49 − 14b + b2 + b2 = 25 → 2b2 − 14b + 24 = 0 ∶ (2) →
b2 − 7b + 12 = 0 → ∆= 49 − 48 → ∆= 1 → 𝑏 =
7±1
→ 𝑏 ′ = 4; 𝑏" = 3
2
Para b = 4 => a = 7 – 4 => a = 3
(iv) Área do retângulo:
S = a. b → S = 3.4 → 𝐒 = 𝟏𝟐
Resposta: C.
207. Os lados de um paralelogramo medem 10 e 6√𝟑. Se seus lados formam 60°, sua área mede:
(a) 90
(b) 120
(c) 60
(d) 75
Solução
(i) No triângulo retângulo ADE, temos:
Seno 60° =
h
6√3
→
ℎ
√3
=
→ 2ℎ = √3. 6√3 →
2
6√3
2ℎ = 18 → ℎ = 9
(ii) Área do paralelogramo:
S = b. h → S = 10.9 → 𝐒 = 𝟗𝟎
Resposta: A
208. A figura representa um triângulo equilátero de lado 6 e seu círculo circunscrito. A área assinalada
mede:
(𝐚) 𝟐𝛑 − √𝟑
(𝐛) 𝟑𝛑 − 𝟐√𝟑
(𝐜) 𝟒𝛑 − 𝟑√𝟑
(𝐝)𝟏𝟐𝛑 − 𝟗√𝟑
Solução 1
12
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(i) No triângulo retângulo ABC, pelo Teorema de Pitágoras,
temos:
62 = h2 + 32 → 36 = h2 + 9 → h2 = 27 → h = √27 →
𝐡 = 𝟑√𝟑
(ii) Área do triângulo equilátero:
S=
b. h
6.3√3
→S=
→ 𝐒 = 𝟗. √𝟑
2
2
(iii) No triângulo AOM, temos:
Cos 30° =
3 √3 3
6 √3
6√3
→
= →R=
.
→R=
→
R
2
R
3
√3 √3
𝐑 = 𝟐√𝟑
(iv) Área do círculo:
2
S = πR2 → S = π(2√3) → 𝐒 = 𝟏𝟐𝛑
Sassinalada =
Scírculo − Striângulo
12𝜋 − 9√3 3
→ Sassinalada =
: → 𝐒𝐚𝐬𝐬𝐢𝐧𝐚𝐥𝐚𝐝𝐚 = 𝟒𝛑 − 𝟑√𝟑
3
3
3
Resposta: C
Solução 2
13
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(i) No triângulo retângulo BOM, temos:
cos 30° =
r=
6
.
3 √3 3
→
= → r√3 = 6 →
r
2
r
√3
√3 √3
→r=
6√3
→ 𝐫 = 𝟐√𝟑
3
(ii) A Altura do triângulo equilátero ABC é dada
por:
h=
L . √3
6. √3
→h=
→ 𝐡 = 𝟑√𝟑
2
2
(iii) Área do triângulo AOC:
√3
√3
(2√3). (2√3). 2
12. 2
𝑟. 𝑟. 𝑠𝑒𝑛 120°
12√3
S∆ =
→ S∆ =
→ S∆ =
→ S∆ =
→ 𝐒∆ = 𝟑√𝟑
2
2
2
4
(iv) Cálculo da área do setor circular AOC:
SetorAOC =
πR²α
π. (2√3)2 . 120°
π. 12
→ SetorAOC =
→ SetorAOC =
→ 𝐒𝐞𝐭𝐨𝐫𝐀𝐎𝐂 = 𝟒𝛑
360°
360°
3
(v) Área assinalada (Área do segmento circular):
Ssegmento = SetorAOC − S∆ → 𝐒𝐬𝐞𝐠𝐦𝐞𝐧𝐭𝐨 = 𝟒𝛑 − 𝟑√𝟑
209. Dois triângulos são semelhantes, sendo a razão de semelhança igual a 3. A razão entre suas áreas
é:
(a) 3
(b) 6
(c) 9
(d) 27
Solução
Quando dois triângulos são semelhantes a razão entre as áreas é igual ao quadrado da razão de semelhança.
Logo:
S′
𝐒′
= (3)² →
=𝟗
S′′
𝐒′′
Resposta: C
14
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
210. Dois círculos de centros A e B e raios R e 4R são tangentes exteriormente. Uma reta é tangente em
C e D aos dois círculos. A área do quadrilátero ABCD é:
(a) 4R²
(b) 5R²
(c) 8R²
(d) 10 R²
(e)
𝟐𝟓𝑹𝟐
𝟐
Solução
(i) àrea do Retângulo:
S = 5R. R → S = 5R²
(ii) Área do Triângulo:
5𝑅. 3𝑅
15𝑅 2
𝑆=
→𝑆=
2
2
(iii) Área do quadrilátero ABCD:
15R2
𝟐𝟓𝐑𝟐
S = àrea do Retângulo + Área do Triângulo → S = 5R +
→𝐒=
2
𝟐
2
Resposta: D
211. Calcule o perímetro de um losango em que uma diagonal mede 10 cm equivalente a um quadrado
de lado igual a 5 cm.
𝟓
(𝐚) √𝟓
𝟐
(𝐛) 𝟓√𝟓
(𝐜) 𝟏𝟎 √𝟓
(𝐝) 𝟓√𝟏𝟎
Solução
(i) Como o losango e o quadrado são equivalentes, possuem áreas iguais. Logo:
Squadrado = L2 → Squadrado = 52 → 𝐒𝐪𝐮𝐚𝐝𝐫𝐚𝐝𝐨 = 𝐒𝐥𝐨𝐬𝐚𝐧𝐠𝐨 = 𝟐𝟓
Slosango = 25 →
D. d
10. d
= 25 →
= 25 → 5d = 25 ∶ (5) → 𝐝 = 𝟓
2
2
15
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
No triângulo retângulo cinza (ao lado), temos:
5 2
25
125
125
L = ( ) + 52 → L2 =
+ 25 → L2 =
→L=√
→
2
4
4
4
2
𝐋=
𝟓√𝟓
𝟐
Perímetro (P) do losango:
P = 4L → P = 4.
5√5
→ 𝐏 = 𝟏𝟎√𝟓
2
Resposta: C
212. Considere dois círculos concêntricos de raios R e 2R e centro O. Considere uma corda AB do
círculo maior tangente ao círculo menor. Se a área do setor AOB é 𝒌𝝅𝑹² , K vale:
(𝐚)
𝟏
𝟐
(𝐛)
𝟑
𝟐
(𝐜)
𝟑
𝟒
(𝐝)
𝟒
𝟑
Solução
Devemos ter o seguinte:
Note que:
(i) A área do círculo maior é igual a:
π(2R)2 = 4𝜋𝑅²
4
Consequentemente: 𝑘 = 𝑚
̅̅̅̅) = 𝑚(𝑂𝐵
̅̅̅̅ ) = 2𝑅
(ii) 𝑚(𝑂𝐴
Considere uma corda AB do A área do setor AOB é 𝒌𝝅𝑹².
círculo maior tangente ao círculo
menor.
Agora, trace um segmento de reta de O até P, que pertence à circunferência, e intersecta ̅̅̅̅̅
𝐴𝐵 em seu ponto
médio M. Esses segmentos são, portanto, perpendiculares.
16
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(iii) Os triângulos BMP e BMO são congruentes por LAL, afinal, ambos
compartilham o mesmo lado BM. Assim sendo:
M(MP) = m(MO) = R.
Segue que: m(BP) = m(BO) = 2R e, assim, conclui-se que o triângulo BPO
é equilátero cujos lados medem 2R.
Por simetria,o mesmo podemos dizer do triângulo APO.
Com isso, finalmente, concluimos que o ângulo AOB = 120°, o que
representa um terço da circunferênciaa. Logo: m = 2 e k = 3/4
Resposta: C
213. Se o raio de um círculo é multiplicado por 2,5, a sua área fica multiplicada por:
(a) 5
(b) 10
(c) 25
(d) 125
(e) NRA
Solução
Vamos supor que o raio original meça 100. Logo, a área do círculo original vale:
S = πr 2 → S = π(100)2 → 𝐒 = 𝟏𝟎. 𝟎𝟎𝟎𝛑
Multiplicando o raio original por 2,5 temos:
100 x 2,5 = 250
Logo, a área final do círculo vale:
𝑆 = πr 2 → S = π(250)2 → 𝐒 = 𝟔𝟐. 𝟓𝟎𝟎𝛑
Portanto, o raio do círculo é multiplicado por:
n=
62.500
→ 𝐧 = 𝟔, 𝟐𝟓 (𝐑𝐞𝐬𝐩𝐨𝐬𝐭𝐚: 𝐃)
10.000
214. A área de um triângulo retângulo em que um cateto mede 45 e a hipotenusa 53 é:
(a) 1260
(b) 930
(c) 760
(d) 630
(e) NRA
Solução
Pelo Teorema de Pitágoras, temos:
(53)2 = x 2 + (45)2
2809 = x 2 + 2025
x 2 = 2809 − 2025
x 2 = 784
x = √784
𝐱 = 𝟐𝟖
17
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
Área do triângulo:
S=
cateto x cateto
45.28
→S=
→ S = 14.45 → 𝐒 = 𝟔𝟑𝟎
2
2
Resposta: D
215. Em um trapézio isósceles de bases 10 e 6, as diagonais são perpendiculares aos lados oblíquos às
bases. A área desse trapézio é:
(a) 32
(b) 28
(c) 24
(d) 20
(e) NRA
Solução
No triângulo retângulo (cinza) destacado ao lado,
temos:
sen 30° =
h 1 h
→ = →𝐡=𝟒
8 2 8
Área do trapézio
S=
(B + b). h
(10 + 6). 4
→S=
→ 𝐒 = 𝟑𝟐
2
2
Resposta: A
217. A área do triângulo da figura é:
(a) 12
(b) 18
(c) 20
(d) 30
(e) 24
Solução
Devemos ter o seguinte:
S=
a. b. sen α
8.4√3. sen 120°
16.3
√3
→S=
→ S = 16√3.
→S=
→ 𝐒 = 𝟐𝟒
2
2
2
2
Resposta: E
18
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(216) O círculo inscrito em um setor de 60° e raio R tem área kR², on de k vale:
(a) 1/4
(b) 1/8
(c) -3/10
(d) 4/15
(e) 1/9
Solução
No triângulo retângulo destacado, temos:
𝑠eno 30° =
R
1
R
→
=
→ R′ − R = 2R → 𝐑′ = 𝟑𝐑
R′ − R
2 R′ − R
218. Um trapézio retângulo de bases 9 e 4 tem diagonais perpendiculares. Sua área é:
(a) 26
(b) 39
(c) 52
(d) 78
(e) NRA
Solução
Como as diagonais são perpendiculares, então o
ângulo entre elas é de 90º. Podemos inserir os
ângulos complementares “a” e “b” no triângulo
DAE. Tenha em mente que “a” e “b” são
complementares, isto é: a + b = 90º.
19
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
Após inserir esses dois ângulos, também
podemos inserir os mesmos ângulos a e
b nos demais triângulos a seguir:
Essa construção é importante para identificarmos que o triângulo DAB (cinza) é semelhante ao triângulo CDA
(amarelo).
Devemos ter:
h 9
= →
4 h
h2 = 36 →
𝐡=𝟔
Área do trapézio
S=
(B + b)h
(9 + 4). 6
→S=
→ S = 13.3 → 𝐒 = 𝟑𝟗
2
2
Resposta: B
20
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
219. A área de um círculo inscrito em um triângulo equilátero é 𝟑𝟔𝝅. A altura desse triângulo mede:
(a) 6
(b) 12
(c) 18
(d) 24
(e) NRA
Solução
(i) Área do círculo
S = 36π
πR2 = 36π
R2 = 36 →
R = √36
𝐑=𝟔
Note que:
h = 3. R
h = 3.6
𝐡 = 𝟏𝟖
Resposta: C
220. Se o raio de um círculo aumenta de 10%, sua área aumenta de:
(a) 10%
(b) 20%
(c) 21%
(d) 100%
(e) NDA
Solução 1
Vamos supor que o raio original do círculo seja igual a 100, logo, sua área original vale:
Soriginal = πr² → Soriginal = π. (roriginal )² → Soriginal = π(100)² → 𝐒𝐨𝐫𝐢𝐠𝐢𝐧𝐚𝐥 = 𝟏𝟎. 𝟎𝟎𝟎𝛑
Aumentando o raio r = 100 em 10% temos como raio final 𝐫𝐟𝐢𝐧𝐚𝐥 = 𝟏𝟏𝟎
Logo, a área final será de:
Sfinal = πr 2 → Sfinal = π. (rfinal )² → Sfinal = π. (110)² → 𝐒𝐟𝐢𝐧𝐚𝐥 = 𝟏𝟐. 𝟏𝟎𝟎
Temos, então, um aumento de:
Aumento = Sfinal − Soriginal → Aumento = 12.100 − 10.000 → 𝐀𝐮𝐦𝐞𝐧𝐭𝐨 = 𝟐. 𝟏𝟎𝟎
Usando uma regra de três simples, temos:
10.000......................100%
21
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
2.100.............................x
𝐱 = 𝟐𝟏%
Resposta: C
Solução 2
A área o círculo de raio r é igual a:
S = πr²
Se o raio r aumentou 10%, temos o novo raio igual a 1,10 r. Logo, a nova área passa a ser igual a:
S = π(110r)2 => S = 1,21πr 2
Logo, houve um aumento de: 1,21πr 2 − πr 2 => 0,21πr 2 x 100 => 𝟐𝟏. 𝛑𝐫²
Resposta: C
221. A área de um hexágono regular inscrito em um círculo de raio 8 é:
(𝐚) 𝟔𝟒√𝟑
(𝐛) 𝟕𝟐√𝟑
(𝐜) 𝟖𝟒√𝟑
(𝐝) 𝟗𝟔√𝟑
(𝐞) 𝐍𝐑𝐀
Solução
Note que o heágono pode ser decomposto em 6 triângulo
equiláteros.
Logo, a área do hexágono é igual a 6 vezes a área do triângulo
equilátero. Assim sendo, temos:
Shex
𝐿2 √3
82 √3
3. 64 √3
= 6.
→ Shex = 6.
→ Shex =
→
4
4
2
Shex = 3.32. √3 → 𝐒𝐡𝐞𝐱 = 𝟗𝟔√𝟑
Resposta: D
222. Os catetos de um triângulo retângulo medem 16 e 30. A área do círculo circunscrito a esse triângulo
é:
(𝐚) 𝟏𝟕𝟒𝛑
(𝐛) 𝟐𝟏𝟏𝛑
(𝐜) 𝟐𝟖𝟗𝛑
(𝐝)𝟑𝟏𝟔𝛑
(𝐞) 𝐍𝐃𝐀
Solução
22
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(ii) No triângulo retângulo ABC, temos:
a2 = (16)2 + (30)2
a2 = 256 + 900
a2 = 1156
a = √1156
a = 34
Note que “a” é o diâmetro do círculo, logo, o raio
mede 17.
(ii) A área do círculo, vale:
S = πr 2 → S = π(17)2 → 𝐒 = 𝟐𝟖𝟗𝛑
Resposta: C
223. O lado de certo quadrado aumenta de 30%. Sua área, então, aumenta de:
(a) 15%
(b) 30%
(c) 60%
(d) 69%
(e) 27%
Solução
Vamos supor que o lado original do quadrado seja igual a 100, logo, sua área original vale:
Soriginal = L² → Soriginal = (100)² → 𝐒𝐨𝐫𝐢𝐠𝐢𝐧𝐚𝐥 = 𝟏𝟎. 𝟎𝟎𝟎
Aumentando o lado L = 100 em 30% temos como lado final 𝐋𝐟𝐢𝐧𝐚𝐥 = 𝟏𝟑𝟎
Logo, a área final será de:
Sfinal = L2 → Sfinal = (Lfinal )² → Sfinal = π. (130)² → 𝐒𝐟𝐢𝐧𝐚𝐥 = 𝟏𝟔. 𝟗𝟎𝟎
Temos, então, um aumento de:
Aumento = Sfinal − Soriginal → Aumento = 16.900 − 10.000 → 𝐀𝐮𝐦𝐞𝐧𝐭𝐨 = 𝟔. 𝟗𝟎𝟎
Usando uma regra de três simples, temos:
10.000......................100%
6.900.............................x
𝐱 = 𝟔𝟗%
Resposta: D
23
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
224. A área de um segmento circular de raio R e ângulo de 60° é:
(𝐚)
𝐑𝟐
𝐑𝟐
(𝐛)
(𝟐𝛑 − 𝟑√𝟑)
(𝟐𝛑 − 𝟑√𝟑)
𝟏𝟐
𝟔
(𝐜)
𝐑𝟐
(𝟐𝛑 − √𝟑)
𝟔
(𝐝)
𝐑𝟐
(𝛑 − √𝟑)
𝟏𝟐
(𝐞) 𝐍𝐑𝐀
Solução
A área do segmento circular é igual à área do setor
circular menos a área do triângulo formada pelos
pontos do setor circular. A fórmula por ângulo em
graus é:
Ssegmento = Ssetor − Striângulo OAB
(i) Descobrimos a área do setor através de uma
regra de três simples:
Área
Ângulo
πR2 … … … … … … 360°
Ssetor … … … … … … â
𝐒𝐬𝐞𝐭𝐨𝐫 =
𝛑. 𝐑𝟐 . â
π. R2 . 60°
𝛑𝐑²
→ Ssetor =
→ 𝐒𝐬𝐞𝐭𝐨𝐫 =
𝟑𝟔𝟎°
360°
𝟔
(ii) A área do triângulo OAB é dada por:
𝐒𝐎𝐀𝐁
√3
R2 . 2
𝐑. 𝐑. 𝐬𝐞𝐧 𝐚̂
R2 . sen â
R2 . sen 60°
=
→ SOAB =
→ SOAB =
→ SOAB =
→
𝟐
2
2
2
𝐒𝐎𝐀𝐁
𝐑𝟐 √𝟑
=
𝟒
(iii) Devemos ter, então:
Sseg = Ssetor − Striân → Sseg =
𝐒𝐬𝐞𝐠 =
πR2 R2 √3
4𝜋𝑅 2 − 6𝑅 2 √3 2
2πR2 − 3R2 √3
−
→ Sseg =
: → Sseg =
→
6
4
24
2
12
𝐑𝟐
(𝟐𝛑 − 𝟑√𝟑)
𝟏𝟐
Resposta: A
225. A área de um segmento circular de raio R e o ângulo central de 30° é:
(𝐚)
𝐑𝟐
𝐑𝟐
𝐑𝟐
(𝛑 − 𝟔) (𝐛) (𝛑 − 𝟑) (𝐜)
(𝛑 − 𝟑)
𝟏𝟐
𝟔
𝟏𝟐
(𝐝)
𝐑𝟐
(𝛑 − 𝟐)
𝟔
(𝐞) 𝐍𝐑𝐀
Solução
24
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(i) Conforme vimos na questão anteriro, a área de um setor
circcular é dada por:
𝐒𝐬𝐞𝐭𝐨𝐫 =
𝛑. 𝐑𝟐 . â
π. R2 . 30°
𝛑𝐑²
→ Ssetor =
→ 𝐒𝐬𝐞𝐭𝐨𝐫 =
𝟑𝟔𝟎°
360°
𝟏𝟐
(ii) Área do triângulo OAB:
SOAB
1
𝑅2. 2
R2 . sen â
R2 . sen 30°
=
→ SOAB =
→ SOAB =
2
2
2
𝐒𝐎𝐀𝐁 =
Ssegmento = Ssetor − Striângulo OAB → Ssegmento =
𝐒𝐬𝐞𝐠𝐦𝐞𝐧𝐭𝐨
𝐑𝟐
(𝛑 − 𝟑)
=
𝟏𝟐
𝐑²
𝟒
πR2 R2
πR2 − 3R2
−
→ Ssegmento =
→
12
4
12
(𝐑𝐞𝐬𝐩𝐨𝐬𝐭𝐚: 𝐂)
226. A razão entre as áreas dos quadrados inscrito e circunscrito ao mesmo círculo é:
(𝐚)
𝟏
𝟐
(𝐛)
𝟐
𝟑
(𝐜)
𝟑
𝟒
(𝐝)
𝟐
𝟓
(𝐞) 𝐍𝐃𝐀
Solução
(i) Note que no quadrado maior (circunscrito ao círculo),
o lado L do quadrado vale 2R. Logo: L = 2R. Portanto, a
área do quadrado circunscrito ao círculo (𝑆1 ) vale:
S1 = (2R)² → 𝐒𝟏 = 𝟒𝐑²
(ii) No quadrado EFGH de lado M, inscrito no círculo, a
diagonal (D) vale 2R. Logo:
D = M√2 → 2R = M√2 → 𝐌 =
𝟐𝐑
√𝟐
(iii) Área do quadrado EFGH (𝑆2 )
2
S2 = M → S2 = (
2R
2
4R²
) → S2 =
→ 𝐒𝟐 = 𝟐𝐑²
2
√2
(iv) Razão entre as áreas dos quadrados inscrito e circunscrito:
Razão =
S2
2R2 2
𝟏
→ Razão =
: → 𝐑𝐚𝐳ã𝐨 =
S1
𝟐
4R² 2
227. A área de um triângulo equilátero circunscrito a um círculo de raio r é:
25
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(𝐚)
𝟓 𝟐
𝐫
𝟐
(𝐛) 𝟑√𝟑 𝐫 𝟐
(𝐜) 𝟑√𝟑 𝛑𝐫 𝟐
(𝐝) 𝛑√𝟑 𝐫 𝟐
(𝐞) 𝐍𝐑𝐀
Solução
No triângulo cinza (destacado), temos:
tg 30° =
L=
r
2
6r
√3
→
= r. → L√3 = 6r → L =
L
3
L
√3
2
6r √3
6r√3
.
→L=
→ 𝐋 = 𝟐𝐫√𝟑
3
√3 √3
A área de um triângulo é dada por:
base x altura
L xh
→S=
→
2
2
2r√3 x 3r
S=
→ 𝐒 = 𝟑√𝟑 . 𝐫²
2
S=
Resposta: B
228. A razão entre as áreas dos triângulos equiláteros inscrito e circunscrito ao mesmo círculo é:
(𝐚)
𝟏
𝟐
(𝐛)
𝟏
𝟑
(𝐜)
𝟐
𝟑
(𝐝)
𝟏
𝟒
(𝐞)
𝟐
𝟓
Solução
Vamos deduzir as fórmulas nos triângulos.
(i) Triângulo inscrito no círculo:
Um triângulo inscrito define três ângulos centrais de 120°. Para
perceber isso, veja que o triângulo equilátero divide a
circunferência em três partes iguais, sendo assim, cada ângulo
interno é a terça parte da circunferência completa:
ai =
360°
→ 𝐚𝐢 = 𝟏𝟐𝟎°
3
26
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
No triângulo destacado, temos:
L
L
√3
(i) sen 60° = 2 →
=
→ 2L = 2r√3 → 𝐋 = 𝐫√𝟑
r
2
2r
(ii) cos 60° =
a 1 a
𝐫
→ = → 2a = r → 𝐚 =
r 2 r
𝟐
O apótema do triângulo equilátero vale 1/3 da altura. Portanto, usando a fórmula da altura de um triângulo
equilátero, temos:
1
r
𝟑𝐫
a = . h → h = 3a → h = 3. → 𝐡 =
3
2
𝟐
(iii) Cálculo da área do triângulo equilátero inscrito:
2
(r√3) . √3
L2 √3
𝟑𝐫 𝟐 √𝟑
S=
→S=
→𝐒=
4
4
𝟒
(iv) No triângulo circunscrito a um círculo, temos:
No triângulo destacado, temos:
tg 30° =
L=
r
2
6r √3
√3
→
= r. → L√3 = 6r → L =
.
→
L
3
L
√3 √3
2
6r√3
→ 𝐋 = 𝟐𝐫√𝟑
3
(v) Área do triângulo equilátero circunscrito a um círculo:
S=
bxh
L x 3r
2r√3 x 3r
→S=
→S=
→ 𝐒 = 𝟑𝐫²√𝟑
2
2
2
(v) Cálculo da razão entre as áreas dos triângulos equiláteros inscrito e circunscrito ao mesmo círculo
27
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
𝟑𝐫 𝟐 √𝟑
𝟒
𝑟𝑎𝑧ã𝑜 =
→
𝟑𝐫 𝟐√𝟑
𝐑𝐚𝐳ã𝐨 =
𝟏
𝟒
Resposta: D
(229) A razão entre as áreas de um triângulo equilátero inscrito e de um hexágono regular circunscrito
ao mesmo círculo é:
(𝐚)
𝟏
𝟐
(𝐛)
𝟏
𝟒
(𝐜)
𝟐
𝟓
(𝐝)
𝟑
𝟓
(𝐞)
𝟑
𝟖
Solução
(230) Um dos lados oblíquos de um trapézio mede “a” e a distância do ponto médio do lado oposto a
este lado é “x”. A área do trapézio é:
(𝐚)
𝐚𝐱
𝟐
(𝐛) 𝐚𝐱
(𝐜) 𝟐𝐚𝐱
(𝐝) 𝐈𝐧𝐝𝐞𝐭𝐞𝐫𝐦𝐢𝐧𝐚𝐝𝐨
(𝐞) 𝐍𝐑𝐀
Solução
(231) No quadrilátero qualquer ABCD, P é meio de AD e M é meio de BC. Se a área de ABCD é 18, a
área do quadrilátero APCM é:
(a) 6
(b) 9
(c) 12
(d) Indeterminado
(e) NRA
246. Calcule a área assinalada:
(𝐚)
𝛑𝐑𝟐
𝟒
𝛑𝐑𝟐
(𝐛)
𝟖
(𝐜)
𝛑𝐑𝟐
𝟏𝟔
𝛑𝐑𝟐
(𝐝)
𝟑𝟐
(𝐞) 𝐍𝐑𝐀
28
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
Solução
R
Área do círculo de raio R Área do circulo de raio 2
Área assinalada =
−
4
2
2
Área assinalada =
πR
−
4
R 2
π (2)
2
R2
π.
πR
πR2 πR2 2πR2 − πR2 𝛑𝐑𝟐
→
− 4 →
−
→
→
(𝐑𝐞𝐬𝐩𝐨𝐬𝐭𝐚: 𝐁)
4
2
4
8
8
𝟖
2
247. Considere um triângulo equilátero de lado “a” onde foram traçados três círculos de raios
centro nos vértices. Calcule a área exterior aos círculos e interior ao triângulo equilátero.
(𝐚)
𝐚𝟐
(𝟐√𝟑 − 𝛑)
𝟐
(𝐛)
𝐚𝟐
(𝛑 − √𝟑)
𝟒
(𝐜)
𝐚𝟐
(𝟐√𝟑 + 𝛑)
𝟒
(𝐝)
𝐚𝟐
(𝟐√𝟑 − 𝛑)
𝟖
𝒂
𝟐
com
(𝐞) 𝐍𝐃𝐀
Solução
Área assinalada = Área do triângulo – 3. Área do setor
(i) Área do triângulo equilátero:
𝐒=
𝐚𝟐 √𝟑
𝟒
(ii) Áreas dos setores circulares:
2
S = 3.
πR α
→ S = 3.
360°
a 2
π. (2) . 60°
360°
a2
π. 4
→ S = 3.
→
6
a2
π. 4
𝛑. 𝐚²
S=
→𝐒=
2
𝟖
Área assinalada =
a2 √3 π. a2 2. a2 . √3 − π. a2 𝐚𝟐
−
→
→ (𝟐√𝟑 − 𝛑)
4
8
8
𝟖
Resposta: D
29
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
248. Considere um quadrado de lado “a” e a figura abaixo. Calcule a área assinalada.
(𝐚) 𝐚𝟐 (𝛑 − 𝟐)
(𝐛)
𝐚𝟐
(𝟐𝛑 − 𝟏)
𝟐
(𝐜)
𝐚𝟐
(𝛑 − 𝟐)
𝟐
(𝐝) 𝟐𝐚𝟐 (𝛑 − 𝟏)
(𝐞) 𝐍𝐑𝐀
Solução
Invertendo a posição da figura, temos:
Vamos calcular o valor de uma área sombreada e multiplicar o resultado por 4. Devemos ter, então:
Área da parte final (Sf ) = Área do setor circular – Área do triângulo
30
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
2
Sf =
πr
b. h
−
→ Sf =
4
2
a 2
π (2)
4
a a
a2 a2
2
2
2
2
.
π.
4 − 4 → S = πa − a → S = πa − 2a →
− 2 2 → Sf =
f
f
2
4
2
16
8
16
𝐚𝟐
(𝛑 − 𝟐)(𝐄𝐬𝐭𝐚 á𝐫𝐞𝐚 é 𝐚𝐩𝐞𝐧𝐚𝐬 𝐚 𝐦é𝐭𝐚𝐝𝐞 𝐝𝐚 𝐩é𝐭𝐚𝐥𝐚)
𝐒𝐟 =
𝟏𝟔
A área final total de cada “pétala” vale:
a2
𝐚𝟐
S′ = 2 [ (π − 2)] → 𝐒′ =
(𝛑 − 𝟐)
16
𝟖
Como são 4 “pétalas” esse resultado deve ser multiplicado por 4. Assim sendo, temos:
S′′ = 4 [
a2
𝐚𝟐
(π − 2)] → 𝐒′′ = (𝛑 − 𝟐)
8
𝟐
Finalmente, o valor total da área assinalada vale:
Área assinalada = Área do quadrado – Área total das partes assinaladas
Sassinalada = a2 −
𝐚𝟐
𝟐𝐚𝟐 − 𝐚𝟐
𝐚𝟐
(𝛑 − 𝟐) → Sassinalada =
(𝛑 − 𝟐) → 𝐒𝐚𝐬𝐬𝐢𝐧𝐚𝐥𝐚𝐝𝐚 = (𝛑 − 𝟐)
𝟐
𝟐
𝟐
Resposta: C
249. Considere o quadrante de raio R da figura. Calcule a área assinalada.
(𝐚)
𝛑𝐑𝟐
𝟖
(𝐛)
𝛑𝐑𝟐
𝟏𝟐
(𝐜)
𝟓𝛑𝐑𝟐
𝟐𝟒
(𝐝)
𝛑𝐑𝟐
𝟏𝟔
Solução
Devemos ter o seguinte
31
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
(i) No triângulo retângulo destacado ao lado, temos:
2
2
R
R
( + r) = ( − r) + x 2
2
2
Rr + Rr = x 2
𝐱 𝟐 = 𝟐𝐑𝐫
(ii) No triângulo retângulo destacado ao lado, temos:
(R − r)2 = r 2 + x 2
R2 − 2Rr + r 2 = r 2 + 2Rr
R2 − 2Rr = 2Rr ∶ R → R − 2r = 2r → R = 4r →
𝐫=
𝐑
𝟒
(iii) Área hachurada
Shachurada = Squadrante − Scírculo − Ssemicírculo
Shachurada =
Shachurada
2
R²
πR2
R 2 π 4
=
− π( ) −
4
4
2
Shachurada =
Shachurada
1 2
πR − πr 2 −
4
R 2
π (2)
πR2 πR2 πR²
−
−
4
16
8
4πR2 − πR2 − 2πR2
=
16
𝐒𝐡𝐚𝐜𝐡𝐮𝐫𝐚𝐝𝐚 =
𝛑𝐑𝟐
𝟏𝟔
Resposta: D
32
Questões do Livro: Geometria II (Morgado)
Celso do Rozário Brasil
33