Enviado por
common.user9800
somando-e-subtraindo-com-o-calculo-mental1525

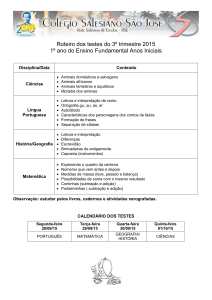
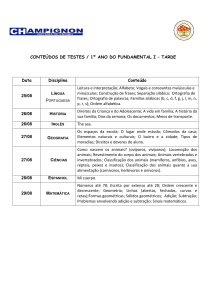
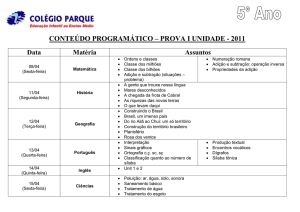
Atividades Objetivo principal Ação principal Tempo sugerido Retomada Relembrar e desenvolver nos alunos habilidades relacionadas ao cálculo mental através de atividades de soma e subtração Entender as estratégias apresentadas, assim como compartilhar outras estratégias e utilizá-las na atividade proposta 12 min Atividade Levar os alunos a utilizarem a estratégia do cálculo mental de maneira lúdica e eficiente para resolver situaçõesproblemas de adição e subtração Utilizar as estratégias apreendidas para resolver as mais diversas contas de adição e subtração que o jogo SomaSub pode propor 18 min Painel de soluções Discutir as estratégias utilizadas, sua efetividade, dúvidas e erros Compartilhar com a turma as estratégias utilizadas, dúvidas, facilidades e dificuldades encontradas durante a atividade 7 min Encerramento Reforçar a importância do cálculo mental no dia a dia e como ele pode facilitar a resolução de problemas Consolidar estratégias e significados relacionados ao uso do cálculo mental 5 min Raio X Verificar e consolidar as aprendizagens dos alunos sobre o uso do cálculo mental para efetuar adições e subtrações Utilizar os saberes e estratégias apreendidos na aula para resolver a situação apresentada e depois comparar as resoluções com as dos colegas. 6 min Objetivo: Utilizar a estratégia do cálculo mental com eficiência para resolver situações-problemas de adição e subtração As operações de soma e subtração têm grande importância em nossa vida e são frequentemente utilizadas por pessoas do mundo todo. Muitas vezes nos mantemos restritos a utilizar os algoritmos para resolver operações de soma ou subtração, ou até mesmo fazer rabiscos, palitinhos, entre outros métodos. Entretanto, nem sempre temos um lápis, caderno ou outros objetos que nos auxiliem a fazê-los. Felizmente, há outras formas mais práticas de se fazer esses cálculos. Uma dessas formas é utilizando o cálculo mental. Para entender melhor como funciona o cálculo mental, vamos revisitar algumas propriedades: A adição possui algumas características importantes que podem facilitar bastante nossos cálculos: Propriedade associativa: Em adições como 3 + 2 + 5 podemos somar inicialmente 3 + 2 e seu resultado com 5, ou ainda 2 + 5 e seu resultado com 3, assim: (3 + 2) + 5 = 3 + (2 + 5) = 10. Propriedade comutativa: Em adições como 5+ 7, podemos somar 5 + 7 = 12 e também 7 + 5 = 12. Ou seja, 7 + 5 = 5 + 7 Para entender melhor como funciona o cálculo mental, vamos revisitar algumas propriedades: De acordo com a relação fundamental da subtração, se somarmos o resto de uma subtração ao subtraendo, obtemos o valor do minuendo. Exemplo: 932 - 11 = 921 921 + 11 = 932 Para entender melhor como funciona o cálculo mental, vamos revisitar algumas propriedades: Em subtrações, é possível somar-se ou subtrair-se valores iguais ao minuendo e ao subtraendo, mantendo-se a equivalência entre as operações: Exemplo 1: 83 - 49 = 34 = (83 + 1) - (49 +1) = 84 - 50 = 34 Exemplo 2: 51 - 23 = 28 = (51 - 1) - (23 - 1) = 50 - 22 = 28 Para entender melhor como funciona o cálculo mental, vamos revisitar algumas propriedades: O sistema de numeração decimal apresenta a característica de cada algarismo de seus números representarem uma grandeza, veja o exemplo: O número 56 é composto por 5 dezenas e 6 unidades Já 45 é composto por 4 dezenas e 5 unidades Para somar 56 + 45 + 34, podemos fazer: 56 + 45 + 34 = 50 + 6 + 40 + 5 + 30 + 4 = 50 + 40 + 30 + 6 + 5 + 4 = 50 + 40 + 30 + (6 + 4) + 5 = (50 + 40 + 30 + 10) + 5 Para entender melhor como funciona o cálculo mental, vamos revisitar algumas propriedades: Ainda no sistema de numeração decimal, temos outra característica: Ao somar os números: 1 + 9 ou 2 + 8 ou 3 + 7 ou 4 + 6 ou 5 + 5 Teremos 10 como resultado, ou seja, uma dezena. Veja um exemplo: 93 + 47 = 90 + 3 + 40 + 7 = 90 + 40 + (3 + 7) = 90 + 40 + 10 = (90 + 10) + 40 = 100 + 40 = 140 Tente agora fazer mentalmente as seguintes operações, busque utilizar diferentes estratégias, e anote-as em seu caderno: 289 + 456 = ? 794 - 126 = ? Vamos Jogar? SomaSub Instruções: Lance uma moeda, para definir se o vencedor será o jogador de menor pontuação (cara) ou maior (coroa). Cada jogador, em sua vez, deverá lançar os dois dados juntos, que definirão suas pontuações iniciais. Suas pontuações deverão ser escolhidas estrategicamente, dessa forma, se os dados indicarem os números 5 e 3, poderá ser escolhido o número 35 ou 53. Na segunda rodada, o procedimento se repete, entretanto, um jogador deverá ser escolhido para iniciá-la, jogando os dois dados, escolhendo a pontuação e calculando mentalmente seu resultado da seguinte forma: ● Somando o número formado nessa rodada com o seu resultado anterior, caso esse número seja maior que seu resultado anterior; ● Subtraindo o número formado nessa rodada pelo seu resultado anterior, caso ele seja menor que seu resultado anterior; ● Caso os valores sejam iguais, o jogador deverá passar a vez para o próximo; O resultado de cada jogador deverá ser verificado em uma calculadora e suas estratégias de cálculo mental devem ser anotadas em suas folhas de registros. Se o jogador acertar, poderá continuar no jogo nas próximas rodadas e será a vez do próximo jogador, que deverá fazer os mesmos procedimentos do jogador anterior. Se o jogador errar, deverá sair do jogo, passando a vez para o jogador à sua direita e retornando apenas quando alguém vencer e o jogo reiniciar. Após no máximo 5 rodadas, vencerá o jogador que obtiver o maior ou menor resultado, conforme definido no início, ou ainda o jogador que acertou em mais rodadas. Vamos agora discutir um pouco sobre o jogo SomaSub. ● Qual o valor mais alto que algum membro do seu grupo atingiu? E o mais baixo? ● Qual a maior pontuação que um jogador pode atingir em duas rodadas? E a menor? ● As estratégias da atividade de aquecimento foram úteis? ● Houve alguma soma ou subtração que alguém não conseguiu fazer? ● Como utilizar essas estratégias com números da ordem das centenas? O que muda? Nesta aula, aprendemos mais um pouco sobre a adição e subtração e estratégias que facilitarão bastante nossos cálculos daqui pra frente. Seja somando ou subtraindo, nem sempre precisamos recorrer aos algoritmos para fazer os cálculos e até mesmo podemos “ajustar” os números antes de recorrer ao algoritmo, facilitando os cálculos. Por que não somar 950 + 143 ao invés de 948 + 145? Veja que o resultado é o mesmo. Tente realizar, sem usar o algoritmo ou os dedos, as operações a seguir, registrando em seu caderno apenas diferentes raciocínios que poderiam ser pensados para facilitar a resolução: 823 + 339 = ? 1995 + 23 = ? 512 - 348 = ? Você pode utilizar desenhos, setas, bolinhas, entre outros objetos para explicar seu raciocínio, use sua criatividade.