Enviado por
common.user7346
LISTÃO - TEOREMA DE PITÁGORAS
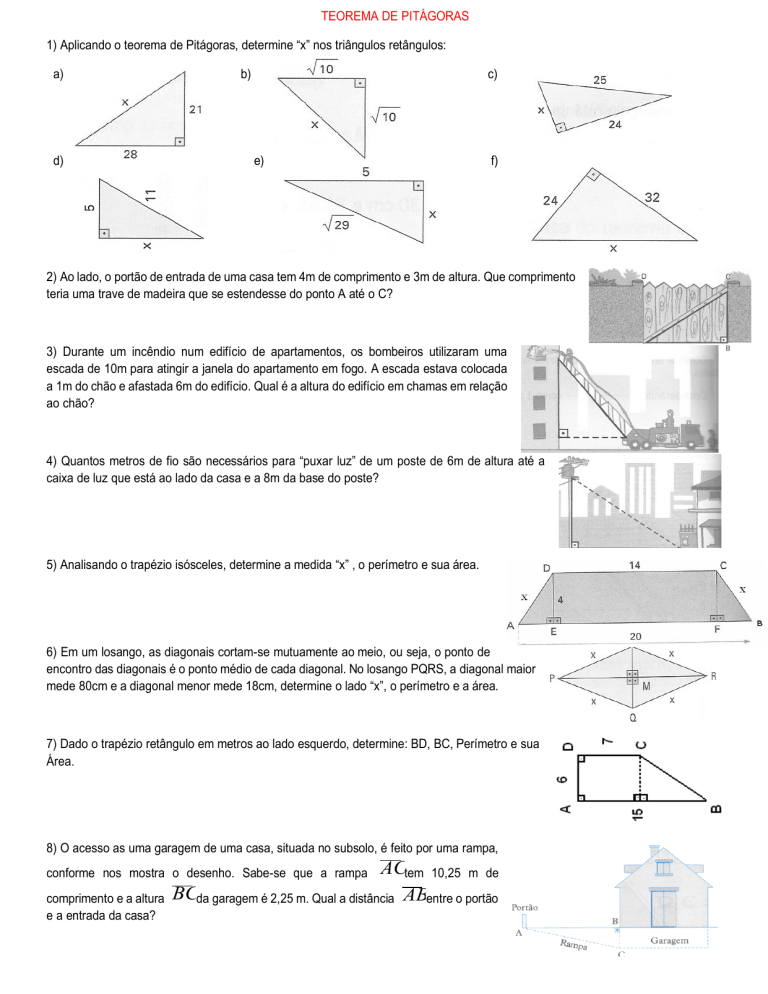
TEOREMA DE PITÁGORAS 1) Aplicando o teorema de Pitágoras, determine “x” nos triângulos retângulos: a) d) b) c) e) f) 2) Ao lado, o portão de entrada de uma casa tem 4m de comprimento e 3m de altura. Que comprimento teria uma trave de madeira que se estendesse do ponto A até o C? 3) Durante um incêndio num edifício de apartamentos, os bombeiros utilizaram uma escada de 10m para atingir a janela do apartamento em fogo. A escada estava colocada a 1m do chão e afastada 6m do edifício. Qual é a altura do edifício em chamas em relação ao chão? 4) Quantos metros de fio são necessários para “puxar luz” de um poste de 6m de altura até a caixa de luz que está ao lado da casa e a 8m da base do poste? 5) Analisando o trapézio isósceles, determine a medida “x” , o perímetro e sua área. 6) Em um losango, as diagonais cortam-se mutuamente ao meio, ou seja, o ponto de encontro das diagonais é o ponto médio de cada diagonal. No losango PQRS, a diagonal maior mede 80cm e a diagonal menor mede 18cm, determine o lado “x”, o perímetro e a área. 7) Dado o trapézio retângulo em metros ao lado esquerdo, determine: BD, BC, Perímetro e sua Área. 8) O acesso as uma garagem de uma casa, situada no subsolo, é feito por uma rampa, ACtem 10,25 m de BCda garagem é 2,25 m. Qual a distância ABentre o portão conforme nos mostra o desenho. Sabe-se que a rampa comprimento e a altura e a entrada da casa? 9) Em um recente vendaval, um poste de luz de 9 metros de altura quebrou-se em um ponto a distância x do solo. A parte do poste acima da fratura inclinou-se e sua extremidade superior encostou no solo a uma distância de 3 m da base do mesmo. Logo, a hipotenusa vale (9-x) metros. A que altura x do solo o poste quebrou? 10) Calcule as medidas indicadas nos triângulos retângulos e sua área e perímetro. 11) O jardim da casa de Maria é formado por cinco quadrados de 12) A figura abaixo é formada por três quadrados de lado 1 e igual TT e tem a forma da figura abaixo. Se AB = 10 m, então a área um retângulo que os contorna. A área do retângulo que do jardim em metros quadrados é: contorna é: A) 200 B) 10 5 C) 100 D) 500 3 E) 100 3 A) 32 B) 4 2 C) 6 A B 13) A distância do menino ao poste é de 12 metros, sabendo que o menino tem 1,60m e a altura do poste é de 6,60m, a que distância está a pipa do menino? 14) (IFRS - 2016) Na figura abaixo, o valor de x e y, é:espectivamente, é D) 6 2 E) 8 15) (IFRJ – 2013) O pátio de esportes do Campus Arrozal de um Instituto Federal é retangular, com 100 m de comprimento e 50 m de largura, representado pelo retângulo ABCD desta figura. Alberto e Bruno são dois alunos, que estão praticando esportes no pátio. Alberto caminha do ponto A ao ponto C pela diagonal do retângulo e volta ao ponto de partida pelo mesmo caminho. Bruno parte do ponto B, dá uma volta completa no pátio, andando pelas linhas laterais, e volta ao ponto de partida. Assim, considerando √5 = 2,24 , afirma-se que Bruno andou mais que Alberto a) 38 m. b) 64 m. c) 76 m. d) 82 m. 16) (Enem – 2017) Para decorar uma mesa de festa infantil, um chefe de cozinha usará um melão esférico com diâmetro medindo 10 cm, o qual servirá de suporte para espetar diversos doces. Ele irá retirar uma calota esférica do melão, conforme ilustra a figura, e, para garantir a estabilidade deste suporte, dificultando que o melão role sobre a mesa, o chefe fará o corte de modo que o raio r da seção circular de corte seja de pelo menos 3 cm. Por outro lado, o chefe desejará dispor da maior área possível da região em que serão fixados os doces. Para atingir todos os seus objetivos, o chefe deverá cortar a calota do melão numa altura h, em centímetro, igual a 17) Enem - 2016 (2ª aplicação) A bocha é um esporte jogado em canchas, que são terrenos planos e nivelados, limitados por tablados perimétricos de madeira. O objetivo desse esporte é lançar bochas, que são bolas feitas de um material sintético, de maneira a situá-las o mais perto possível do bolim, que é uma bola menor feita, preferencialmente, de aço, previamente lançada. A Figura 1 ilustra uma bocha e um bolim que foram jogados em uma cancha. Suponha que um jogador tenha lançado uma bocha, de raio 5 cm, que tenha ficado encostada no bolim, de raio 2 cm, conforme ilustra a figura 2. Considere o ponto C como o centro da bocha, e o ponto O como o centro do bolim. Sabe-se que A e B são os pontos em que a bocha e o bolim, respectivamente, tocam o chão da cancha, e que a distância entre A e B é igual a d. Nessas condições, qual a razão entre d e o raio do bolim?