Módulo 4 Ajuste de Curvas

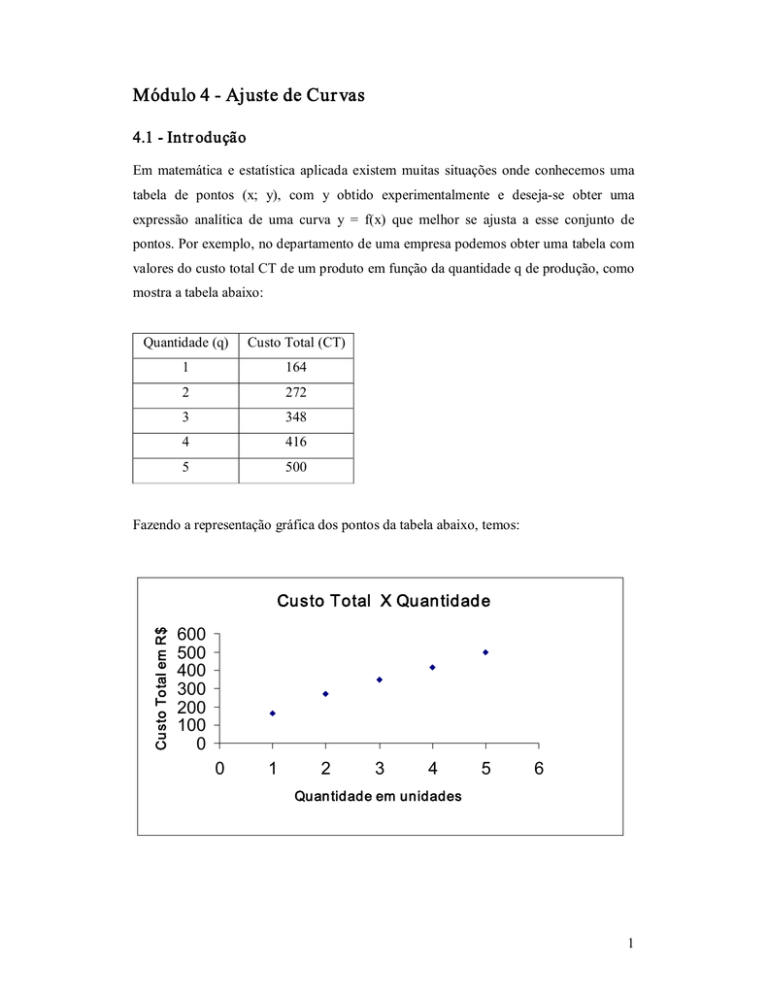
Módulo 4 ­ Ajuste de Cur vas 4.1 ­ Intr odução Em matemática e estatística aplicada existem muitas situações onde conhecemos uma tabela de pontos (x; y), com y obtido experimentalmente e deseja­se obter uma expressão analítica de uma curva y = f(x) que melhor se ajusta a esse conjunto de pontos. Por exemplo, no departamento de uma empresa podemos obter uma tabela com valores do custo total CT de um produto em função da quantidade q de produção, como mostra a tabela abaixo: Quantidade (q) Custo Total (CT) 1 164 2 272 3 348 4 416 5 500 Fazendo a representação gráfica dos pontos da tabela abaixo, temos: Custo Total em R$
Custo Total X Quantidade 600 500 400 300 200 100 0 0 1 2 3 4 5 6 Quantidade em unidades 1 Observe no gráfico acima que não passa uma reta por todos os pontos, então podemos fazer as seguintes perguntas: 1) Qual a curva que melhor se adapta para o conjunto de pontos, isto é, qual expressão analítica ou a função que melhor se ajusta para os pontos (x; y)? 2) Qual a previsão do custo total para 10 unidades do produto? Existem vários modelos matemáticos e estatísticos que resolvem este problema, particularmente nesta unidade vamos estudar o Método dos Mínimos Quadrados (MMQ) que descreveremos a seguir. 4.2 ­ Método dos Mínimos Quadrados (MMQ) O método dos mínimos quadrados é um dos mais simples e poderoso método da análise de regressão. Utilizamos este método quando temos uma distribuição de pontos e queremos ajustar a melhor curva a este conjunto de dados. 4.2.1 ­ Regr essão linear Inicialmente, vamos analisar o caso em que a curva de ajuste é uma função linear : y = ax + b, cujo gráfico é uma reta. A equação da reta ou a função que aproxima o conjunto de pontos é dada por: y = Ax + B A = å x . y - n . x . y 2 2 å x - n x ()
e B = y - A x 2 Onde: n = número de pontos observados
å x = soma dos valores de x (abcissas)
å y = soma dos valores de y (ordenadas)
å x. y = soma dos produtos entre x e y
2
å x x = = soma dos quadrados dos valores de x å x n y = e å y n (Médias Aritméticas) Vamos aplicar o modelo para responder as duas perguntas do problema inicialmente proposto na unidade. Para facilitar os cálculos construímos a tabela e calculamos os elementos da fórmula do Método dos Mínimos Quadrados, onde y representa o custo total CT e x representa a quantidade q. Soma= å x y x.y x 2 1 164 164 1 2 272 544 4 3 348 1044 9 4 416 1664 16 5 500 2500 25 15 1700 5916 55
3 x = å x 15
=
= 3 n 5 y = å y 1700
=
= 340 n 5 A = 5916 - 5 . 3 . 340 816 =
= 81 , 6 2
10 55 - 5 . 3 B = 340 - 81 , 6 . 3 = 95 , 20 Substituindo os valores de A e B, a equação da reta que aproxima os pontos da tabela é: y = 81, 6 x + 95 , 20 isto é, CT = 81, 6 q +
95 , 20 e a previsão para a quantidade q = 10 unidades é dada por: q = 10 Þ CT = 81,6. 10 + 95,20 = 911,20 Assim, o custo total para 10 unidades é de R$ 911,20. Graficamente,
4 Custo Total em R$ Custo Total X Quantidade 600 500 400 300 200 100 0 y = 81,6x + 95,2 0 1 2 3 4 5 6 Quantidade em unidades Box: O símbolo å é a repr esentação de um somatór io. 4.2.2 ­ Regr essão Quadr ática Em muitos problemas de Matemática Aplicada, é comum ocorrerem situações onde a curva de ajuste não é uma reta, podendo os pontos se aproximarem de uma curva cujo gráfico é uma função quadrática, exponencial, logarítmica e outras. Vamos analisar o caso em que a curva de ajuste é uma função quadrática : y = ax 2 + b.x + c. O modelo de ajuste da regressão quadrática é dado por: y = Ax + Bx + C onde: A, B e C é uma solução do sistema de equações lineares abaixo:
ì A å x 4 + B å x 3 + C å x 2 = å x 2 y ïï
3 2 í A å x + B å x + C å x = å xy ï
2 ïî A å x + B å x + C . n = å y Exemplo: A tabela a seguir apresenta os valores da quantidade demandada de um bem e os preços de venda correspondentes em determinado período: Preço de venda 150 185 210 173 145
5 Quantidade vendida 15 38 59 80 100 Ajuste uma parábola para os dados da tabela e projete a quantidade vendida para um preço de venda igual a R$ 120,00. Solução: Inicialmente marcamos os pontos num gráfico para verificar se os pontos tendem mesmo a uma parábola. Quantidade em (unidades) Quantidade X Preço de venda 240 200 160 120 80 40 0 0 15 30 45 60 75 90 105 Preço de Venda (R$) Para facilitar os cálculos construímos uma tabela e calculamos os elementos da fórmula do ajuste da parábola, onde y representa a quantidade e x o preço de venda e na última linha os somatórios das colunas. x y x.y x 2 x 3 x 4 x 2 . y 15 150 2250 225 3375 50625 33750 38 185 7030 1444 54872 2085136 267140 59 210 12390 3481 205379 12117361 731010 80 173 13840 6400 512000 40960000 1107200 100 145 14500 10000 1000000 100000000 1450000 292 863 50010 21550 1775626 155213122 3589100 Substituindo os valores obtidos da tabela acima no sistema de equações e resolvendo, obtemos: A = ­0,0298 B = 3,3416 e C = 105,95
6 A equação que aproxima os pontos da tabela é: y = ­0,0298x 2 + 3,3416x + 105,95 2 isto é, q = ­0,0298 p + 3,3416 p + 105,95 onde: q representa a quantidade demandada e p o preço de venda. Calculando a projeção da quantidade para o preço de venda igual a R$ 120,00 temos; p = 120 Þ q = ­0,0298. (120) 2 + 3,3416. 120 + 105,95 = 77,82 Assim, a quantidade demandada para o preço de R$ 120,00 é de 77,82 unidades. Graficamente, Quantidade em (unidades) Quantidade X Preço de venda 2 y = ­0,0298x + 3,3416x + 105,95 240 200 160 120 80 40 0 0 15 30 45 60 75 90 105 Preço de Venda (R$) Box: O estudo das Regr essões é muito aplicado em pr oblemas de Estatística. 4.3 Ajuste de Curvas no Micr osoft Excel No exemplo de regressão quadrática percebemos a dificuldade em resolver o sistema linear com os coeficientes calculados na tabela, podemos utilizar o Microsoft Excel para determinar a curva de ajuste e também escrever sua respectiva equação. Os passos a
7 seguir podem ser usados para aproximar curvas para o caso linear, quadrática, polinomiais, exponenciais e logaritmicas. Sejam os pares ordenados (x; y), valores retirados de uma tabela, por exemplo: demanda e oferta em função do preço ou custo total, receita total e lucro total em função da quantidade. Para achar a equação da curva que ajusta os pontos da tabela, seguir os seguintes passos: 1. Selecionar os pares ordenados da tabela; 2. Na barra de ferramentas do Microsoft Excel, clicar em assistente gráfico;
· Tipo de gráfico: use dispersão (X;Y);
· Subtipo de gráfico: use dispersão com pontos de dados conectados por linhas;
· Tipos personalizados: use linhas em 2 eixos;
· Concluir 3. Clicar sobre a linha formada pelos pares ordenados; 4. Na barra de ferramentas do Microsoft Excel, clicar em Assistente gráfico;
· Selecione: Adicionar linha de tendência;
· Tipo, marcar: Linear (Função do 1º grau) ou Polinomial – Ordem 2 (Função do 2° grau);
· Opções, selecionar: Exibir equação no gráfico;
· OK O gráfico feito mostra a linha de tendência (ajuste) dos pontos e a equação da curva que foi ajustada conforme o aspecto dos pontos inicialmente marcados com a escolha da função apropriada, como por exemplo: linear, polinomial de grau 2, exponencial ou logaritmica.
8