Problemas Enganadores A chave do sucesso dos Algoritmos

Problemas Enganadores
A chave do sucesso dos Algoritmos Evolucionários é a habilidade deles em combinar blocos
construtivos (Building Blocks - BB) de pequena ordem para formar BB de ordem maior, podendo,
eventualmente, levar à solução ótima do problema. Quando a solução do problema não pode ser
construída através desta combinação incremental de BB, estamos na presença de problemas
enganadores (deceptive problems) ou problemas de armadilha (trap problems/functions) e se faz
necessário melhorar o processo de evolução artificial para contornar este problema. O conceito de
'enganação' (deception) for primeiramente introduzido por Goldber em 1987.
Goldberg criou a função F3 com 3 bits para ilustrar este conceito onde BBs de ordem n são
enganadores para BBs de ordem n+1. Esta função é conhecida como Fully deceptive F3 Function
onde o objetivo é de maximização com o seguinte mapeamento:
F3(000) = 28, F3(001) = 26, F3(010) = 22, F3(011) = 0 F3(100) = 14, F3(101) = 0, F3(110) = 0,
F3(111) = 30
Para tornar este problema desafiador, a função F3 pode ser concatenada com cópias consecutivas de
sua definição. Este procedimento é usual na otimização deste tipo de problema. Por exemplo, F3 10
concatena a função F3 dez vezes, levando a uma quantidade de 30 bits em sua definição e ponto
ótimo em 300.
O problema se torna mais difícil quando os bits de cada função estão separados. O caso mais difícil
de separação ocorre quando os bits estão uniforme e maximamente distribuídos no cromossomo. No
exemplo da função F3 tem-se a função F3S N, onde N representa o número de funções F3 no
cromossomo. No caso da F3S 10, cada bit de uma função está localizado nas posições i, i+10, e
i+20, respectivamente. Generalizando tem-para F3S N se a seguinte distribuição dos bits no
cromossomo: posições i, i+10, i+20, ..., i+10*(N-1), respectivamente.
Em 1987, Ackley introduziu outra trap function conhecida por atuar no espaço unitário e chamada
de Deceptive N, onde N é a quantidade de bits sendo utilizado. Neste espaço somente os valores 1
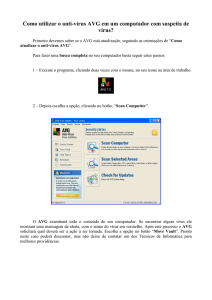
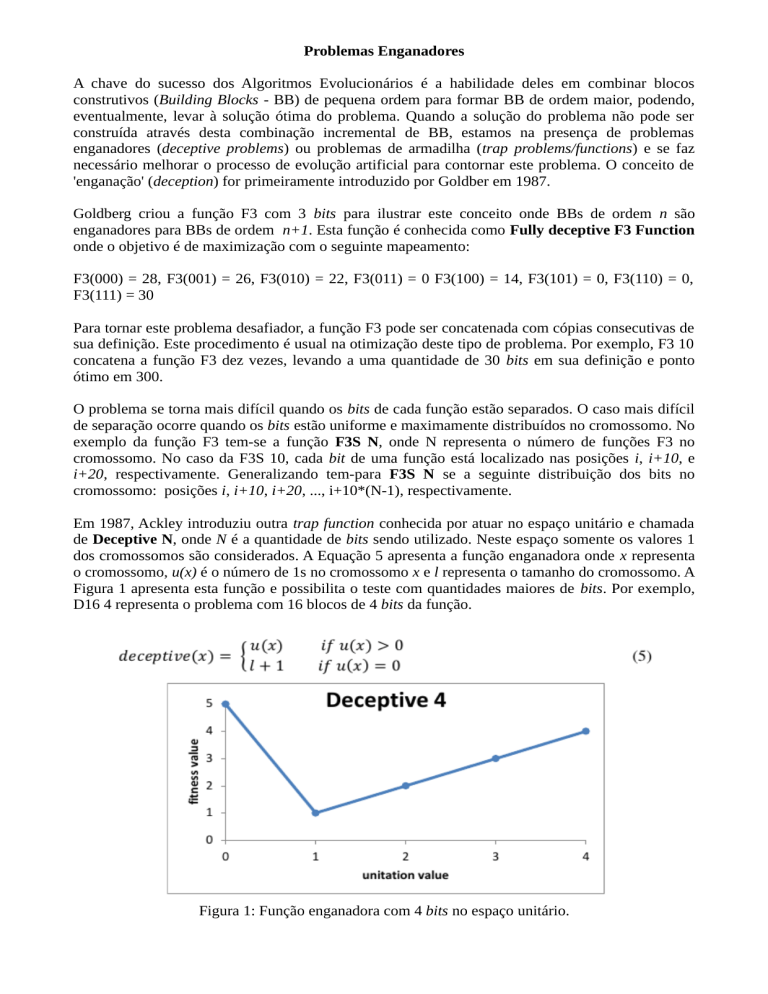
dos cromossomos são considerados. A Equação 5 apresenta a função enganadora onde x representa
o cromossomo, u(x) é o número de 1s no cromossomo x e l representa o tamanho do cromossomo. A
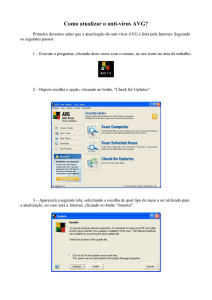
Figura 1 apresenta esta função e possibilita o teste com quantidades maiores de bits. Por exemplo,
D16 4 representa o problema com 16 blocos de 4 bits da função.
Figura 1: Função enganadora com 4 bits no espaço unitário.
Compare os resultados obtidos com o AG com os resultados obtidos com o algoritmo Simulated
Annealing (SA). Considere 10 execuções para cada algoritmo em um máximo de 50,000 avaliações
de função para cada um. Trace os gráficos de convergência e diversidade para o AG e o gráfico de
convergência para o SA. Reporte os resulados nos moldes da Tabela 1. Faça a análise dos resultados
obtidos.
F3 10
AG
SA
Média do melhor valor
Avg +/- std
Avg +/- std
Número de Avaliações para
encontrar o ótimo
Avg +/- std
Avg +/- std
AG
SA
Média do melhor valor
Avg +/- std
Avg +/- std
Número de Avaliações para
encontrar o ótimo
Avg +/- std
Avg +/- std
AG
SA
Média do melhor valor
Avg +/- std
Avg +/- std
Número de Avaliações para
encontrar o ótimo
Avg +/- std
Avg +/- std
AG
SA
Média do melhor valor
Avg +/- std
Avg +/- std
Número de Avaliações para
encontrar o ótimo
Avg +/- std
Avg +/- std
AG
SA
Média do melhor valor
Avg +/- std
Avg +/- std
Número de Avaliações para
encontrar o ótimo
Avg +/- std
Avg +/- std
AG
SA
Média do melhor valor
Avg +/- std
Avg +/- std
Número de Avaliações para
encontrar o ótimo
Avg +/- std
Avg +/- std
Taxa de Sucesso (%)
F3 20
Taxa de Sucesso (%)
F3S 10
Taxa de Sucesso (%)
F3S 20
Taxa de Sucesso (%)
D16 4
Taxa de Sucesso (%)
D32 4
Taxa de Sucesso (%)
Tabela 1: Exemplo de resultados a serem analisados comparando-se GA e SA para um número préfixado de execuções e um número máximo de avaliações de função.