Terceira lista de Máquinas Elétricas II

Terceira lista de Máquinas Elétricas II
Engenharia Elétrica – IFG Campus Jataí
Prof. Marcelo
1) A reatância Xd e Xq de um gerador síncrono de pólos salientes valem 1 e 0,6 pu,
respectivamente. A resistência de armadura é desprezível. Calcule a tensão de
excitação quando o gerador fornece a potência nominal com fp 0,8 indutivo e
tensão terminal nominal.
2) Uma máquina síncrona de pólos salientes, ligada ao barramento infinito, tem os
seguintes dados:
S = 10 KVA, V = 416 V, fp = 0,8 ind, Xd = 1 pu, Xq = 0,7 pu
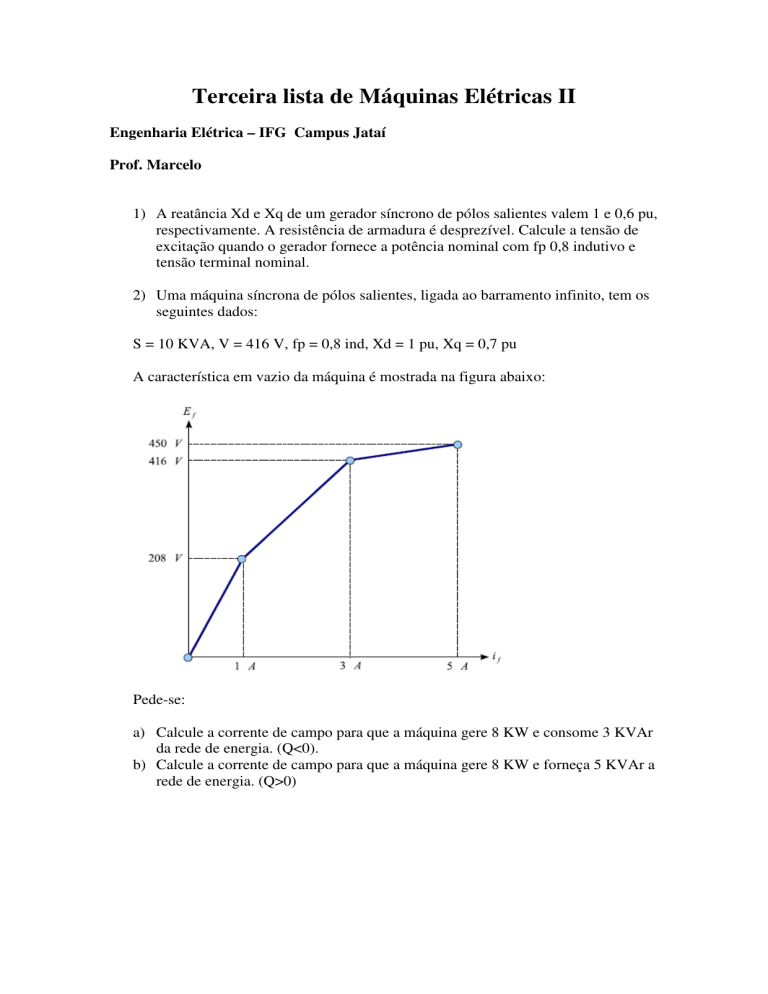
A característica em vazio da máquina é mostrada na figura abaixo:
Pede-se:
a) Calcule a corrente de campo para que a máquina gere 8 KW e consome 3 KVAr
da rede de energia. (Q<0).
b) Calcule a corrente de campo para que a máquina gere 8 KW e forneça 5 KVAr a
rede de energia. (Q>0)
3) Um gerador síncrono de polos salientes apresenta reatâncias síncronas Xd = 1,70
pu e Xq = 1,20 pu.
a) Determine o ângulo de potência δ e o módulo da tensão gerada em pu
(força eletromotriz), quando o gerador está conectado a um barramento
infinito (tensão nominal) e trabalha em corrente terminal nominal com
fator de potência de 0,72 atrasado.
b) Considerando operação com o mesmo ângulo de potência δ do item (a),
determine o módulo da tensão gerada em pu (força eletromotriz) para
que a máquina forneça metade da potência nominal com fator de
potência unitário.
4) Um motor síncrono trifásico de 2000 cv, seis pólos, ligado em Y, 2300 V e 60
Hz opera com fator de potência unitário e possui reatâncias síncronas de eixo
direto e de eixo quadratura de 1,95 Ω/fase e 1,40 Ω/fase, respectivamente. O
motor é alimentado por um barramento infinito em tensão nominal e fornece
80 % da potência nominal à carga conectada no eixo. (a) Determine a corrente
de armadura Ia. (b) Determine o ângulo de potência δ do motor. (c) Determine
as componentes de corrente de eixo direto e de eixo quadratura. (d) Determine a
tensão gerada por fase Ef. (e) Esboce o diagrama fasorial do motor, indicando a
tensão de armadura por fase, a corrente de armadura, as quedas nas reatâncias de
eixo direto e quadratura e a tensão gerada.
5) Refaça o item 4 para o mesmo motor trifásico ligado em ∆.
6) Um gerador síncrono de 311 MVA, 13,8 KV, 36 pólos, é ligado a um
barramento infinito. Seus parâmetros são Xd = 0.9119 pu e Xq = 0,6417 pu e Ra
= 0,01 pu. Considerando que o gerador fornece potência nominal com fp = 0,92
atrasado, determine:
a) Corrente de armadura.
b) As componentes de eixo direto e em quadratura da corrente.
c) A tensão de excitação e o ângulo de carga.
7) Se a potência da máquina primária do exercício anterior for reduzida em 10 %,
repita os itens a, b e c.
8) Se a potência reativa da máquina do exercício 6) dobrar, mantendo a mesma
potência na máquina primária, determine o módulo da tensão de excitação.
9) Um gerador síncrono trifásico de pólos salientes apresenta os seguintes dados de
placa:
100 MVA, 15 KV, conexão em Y e parâmetros iguais a 1 pu, 0,6 pu e 0,3 pu.
Em um dado momento este gerador opera ligado a um barramento infinito cuja
tensão de linha é igual a 15,5 KV, operando com potência de 86,61 MW – j50 MVAr.
Pede-se:
a) Determine a tensão Ef do gerador. R: 10459,86∠
∠33,09º V
b) Trace o diagrama fasorial correspondente.
c) O ângulo de carga δ para que a potência ativa transferida seja máxima. R: 66,82º
10) Um gerador síncrono de pólos salientes tem reatâncias síncronas saturadas Xd =
0,961 pu e Xq = 0,577 pu e está ligado em um barramento infinito com tensão
nominal. O gerador fornece ao sistema potência nominal com fator de potência
0,8 indutivo. Determine:
a) A tensão de excitação em pu. R: 1∠
∠18,44º V
b) Trace o diagrama fasorial.
c) Determine a equação da potência pu em função do ângulo de carga (δ)
para a máquina síncrona.
d) Determine a potência pu máxima que este gerador pode fornecer.
e) Se a potência ativa dobrar, a máquina perderá o sincronismo?
11) Um gerador síncrono trifásico de 2 MW, fator de potência unitário, ligado em
estrela, 2,2 kV, tem reatâncias Xd = 1,5 Ω e Xq = 0,9 Ω. Todas as perdas podem
ser desprezadas. Pede-se: (a) o ângulo de carga quando a máquina funciona com
tensão nominal e carga nominal; (b) a máxima potência ativa que esse gerador
pode fornecer, quando conectado em paralelo a um barramento infinito; (c) o
respectivo ângulo de estabilidade estática.
Ef = 1464,93∠
∠20,4º V
P = 4199398,43 W
δ = 66,65º
12) Considere um gerador síncrono de polos salientes com as seguintes reatâncias
Xd = 0,9 pu, Xq = 0,65 pu. Considere que a potência ativa máxima que esse
gerador pode fornecer é 1 pu, operando sob tensão nominal. Para que não haja
perda de sincronismo, nessa condição, o limite para δ é 60°. Qual deve ser a
tensão de excitação nesse caso?
13) Explique o efeito da saliência dos pólos na máquina síncrona.
14) Explique porque os geradores síncronos apresentam diferentes valores de
reatâncias nos períodos subtransitório, transitório e permanente, quando sujeitos
a curto-circuitos.